|
|
© 2004 Tonalsoft Inc. |
|
|
© 2004 Tonalsoft Inc. |
devised by George Secor, and Dave Keenan and Paul Erlich
©2001 by Joe Monzo
In April 2001, Paul Erlich and Dave Keenan were responding to a request from Joseph Pehrson, on the Yahoo Tuning List, for good 19-tone 11-limit subsets of 72-EDO.
Dave realised that, although there was no obvious winner, most of the good ones were subsets of a particular 31 tone periodicity block which was very even melodically. It was a 72-EDO tempering of a 31-tone planar microtemperament that he had created in December 1999 in collaboration with Paul Erlich and Carl Lumma.
Dave posted this 31-tone scale to the tuning list, whereupon Paul Erlich pointed out that:
Paul suggested that Blackjack would be an excellent name for the latter.
Then Dave Keenan performed a computer-assisted search for other single-chain 11-limit generators which either gave no fewer hexads per note at greater accuracy, or gave more 11-limit quasi-just hexads per note. He repeated the search at the 7-limit (for tetrads instead of hexads). There were none. In fact no other generator even came close.
This generator divides the 12-EDO "5th" into 6 logarithmically equal parts or steps, whereas it is usually divided into 7. In mathematical language this is described as (2(7/12))(1/6) [= 116&2/3 cents]. Thus it also divides the "neutral 3rd" into 3 equal parts. (See Graham Breed's neutral 3rd lattices.)
Any tuning with a generator in the range between 116.1 cents (= 31-EDO) and 117.8 cents (= 0.7 cents larger than 41-EDO) has MIRACLE properties, but that of 72-EDO comes closest to the optimal generators calculated by a number of methods (including root mean square and maximal absolute). There is no single optimum MIRACLE generator; many different kinds of optimum are within 0.15 cent either side of 72-EDO.
(At the time of its rediscovery in April 2001, Dave, Paul, and Carl were all unaware that George Secor had published this generator -- but not the MOS scales -- in 1975, in his article A New Look at the Partch Monophonic Fabric, originally appearing in Xenharmonik˘n 3. In honor of George, this interval was subsequently named the secor.)
Graham Breed has pointed out that 10- and 11-EDO, whose generators lie a bit outside this range, exhibit some of the same melodic properties as the MIRACLE scales. These facts:
have led Graham to advocate the use of a decimal-based notational system for scales in the MIRACLE family. (See also Graham's decimal page.)
The Blackjack generator is also nearly identical to an interval the size of 7 degrees of 72-EDO [= exactly 116 & 2/3 cents, or 1 & 1/6 Semitones]. Thus, it can be represented quite accurately as a 21-out-of 72-EDO tuning. Because of the many useful properties associated with 72-EDO, this greatly simplifies many aspects of the presentation of the Blackjack scale, such as its notation or its diagramming on a lattice.
I will present the Blackjack scale here as 21-out-of-72-EDO. In the 72edo version of blackjack, L is 5 degrees of 72edo and s is 2 degree, so L = 2.5s.
It was decided by Dave and others that "D" should be the reference note for the system, because the layout of notes on the standard Halberstadt keyboard is symmetrical around "D". But I used "C" as the reference in my examples here.
Here is a graph showing the pitch-height of the notes in this scale, within one "octave". Each note is labeled with both my ASCII adaptation of the Sims/Herf 72-EDO notation, and its Semitone value.

Below is a 4-line staff notation I developed for Blackjack, based on Graham Breed's decimal symbology for the MIRACLE family of temperaments. The cents-value is given above the staff, and the 72-EDO degree below.
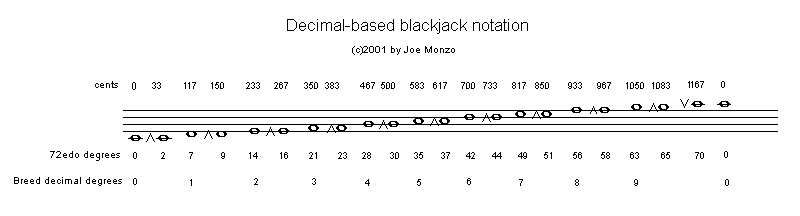
The reference pitch ("0") occurs on the ledger line between staves, and each successive ascending space and line represents the next secor-sized positive generator in the decimal series, and thus the next cardinality in Breed's notation: 1, 2, 3, ... 9, and when that set is exhausted, the next (and last) in the series of generators, 0v, is notated as the "0" reference pitch, an "8ve" higher, accompanied by the v symbol which indicates lowering by a quomma. Descending from the higher "0" ledger-line is the negative series of generators, 9^, 8^, 7^, ... 0^, notated on the same line or space as the namesake cardinality, but accompanied by a ^ symbol to indicate raising by a quomma.
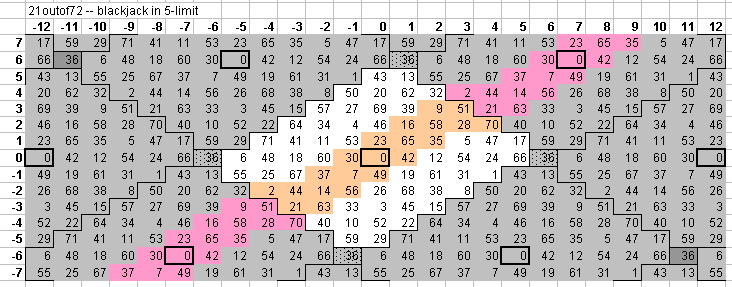
Below is a 5-limit bingo-card-lattice of 72edo, with the blackjack scale shown in buff in the central periodicity-block and in pink in the blocks which are commatic equivalents.
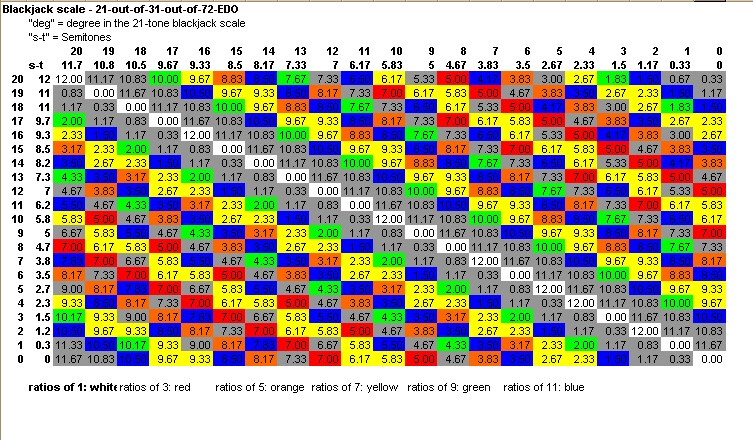
Here is an
interval
matrix chart of all
dyadic
intervals available in the 21-out-of-72 Blackjack scale,
with the pitches labeled with
their 21-tone Blackjack degree numbers and Semitone values.
All interval sizes are shown in Semitones.
(Thanks to Paul Erlich for color-coding the intervals according to the odd- limits of the JI intervals they represent.)
Paul Erlich made a nifty color-coded chart of blackjack intervals (... you have to be a member of Yahoo groups to view it).
Paul also made a 7-limit lattice diagram showing the periodicity blocks implied by the Blackjack tuning, as well as illustrating the many harmonic structures implied by this scale. I have adapted it here to my own ASCII 72-EDO notation. The Blackjack scale is wafso-just with respect to this lattice.

Here is a mapping which I designed, placing 72-EDO onto the fingerboard/keyboard of a Starr Labs Ztar instrument, showing all 72-EDO degrees and their ASCII Monzo notation. The placement of black and white keys reflects the association of various 72-EDO notes with those in 12-EDO as they appear on a regular Halberstadt piano keyboard. The Blackjack notes are shown in orange.
Notice how the placement of the Blackjack notes in the above mapping shifts upward by one key as one travels to the right, because the generator of 7/72 is one more than the 6/72 steps in each column of the keymap.
In the mapping below, I adapted the Starr Labs Zboard keyboard so that each column is 7 steps high, thereby making all the Blackjack notes adjacent.

Graham Breed presented a "comma pump" chord progression in the Blackjack tuning (click on graphic to hear mp3, looped 3 times):
Below is a score of Graham's progression in my 4-line-staff adaptation of Graham's
decimal notation:

Below is a score of the progression notated in my
72edo
HEWM notation:

Below is an applet which shows the 5-limit representation
of Graham's chord progression. Mouse-over the chord-number
(without clicking) to
see a lattice of that chord in red. Commatic equivalents are
shown in purple. Note that Graham's chords all imply a 7-limit
harmony, which is shown in its closest 5-limit approximation (225:128
above the "root" of the chord) here.
Graham's chords are as follows:
chord 72edo
number degree cents
1 70 1167
51 850
28 467
14 233
2 0 0
56 933
37 617
14 233
3 58 967
42 700
23 383
0 0
4 58 967
44 733
28 467
9 150
5 63 1050
44 733
28 467
14 233
6 63 1050
44 733
21 350
7 117
7 70 1167
51 850
35 583
21 350
For the benefit of those wishing to map this family of tunings to a standard 12-tone Halberstadt keyboard, Paul Erlich devised an interesting 12-tone subset of Blackjack, presented in Tuning List post 22532 from Sat May 12, 2001 8:35 am.
Dave Keenan gave an analysis of it in Tuning List post 22622 from Sun May 13, 2001 6:02 am.
Dave also created this diagram of a color-coded design for mapping the full Blackjack scale to the Halberstadt keyboard.
As stated above, 31edo is the tuning which provides
the lower limit of the blackjack generator, so those
who work in 31edo may easily form blackjack as a subset
of that tuning.
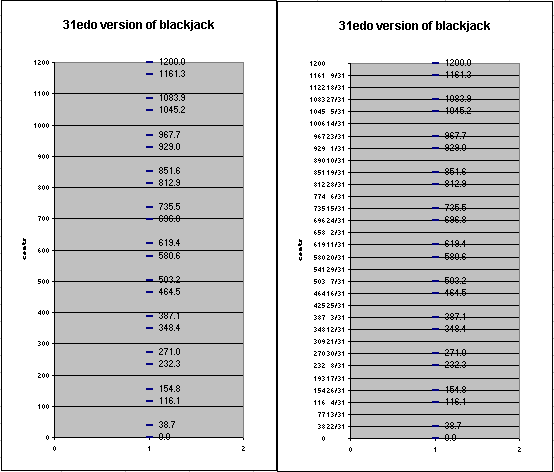
Below is a table showing the degrees of 31edo
which form blackjack:
31edo
degree ~cents
30 1161.3
28 1083.9
27 1045.2
25 967.7
24 929.0
22 851.6
21 812.9
19 735.5
18 696.8
16 619.4
15 580.6
13 503.2
12 464.5
10 387.1
9 348.4
7 271.0
6 232.3
4 154.8
3 116.1
1 38.7
0 0.0
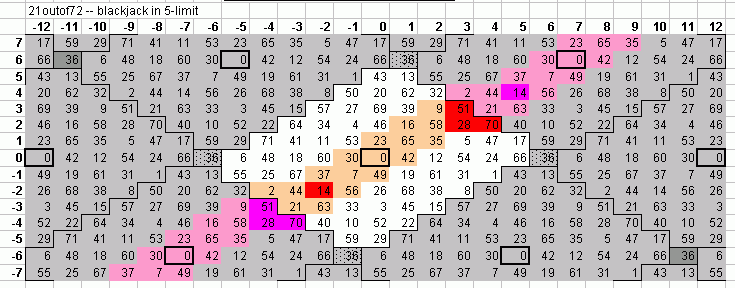
Below are two pitch-height graphs showing the 31edo version of blackjack. The graph on the left has the "octave" divided into 12 steps, and that on the right has it divided into 31 steps.
In the 31edo version of blackjack, L is 2 degrees of 31edo and s is 1 degree, so L = 2s.
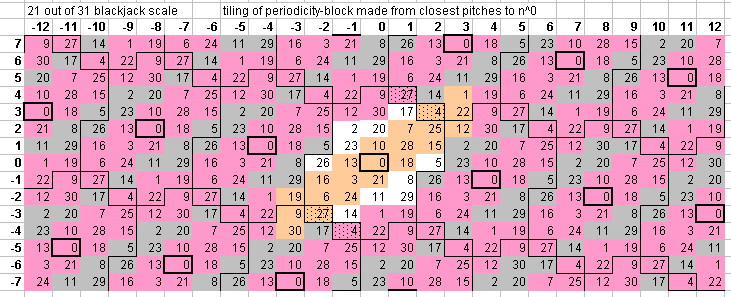
Below is a 5-limit bingo-card-lattice of 31edo, with the 21-tone blackjack scale shown in buff in the central part of the blackjack chain which passes thru n0 and in pink in the chains which are commatic equivalents. The central periodicity-block contains most of the blackjack scale, with 7 of the notes falling into commatically-equivalent chains. The general southwest-to-northeast trend of blackjack is obvious; compare to the 72edo lattice above.
Below are two pitch-height graphs showing the 41edo version of blackjack. The graph on the left has the "octave" divided into 12 steps, and that on the right has it divided into 41 steps.
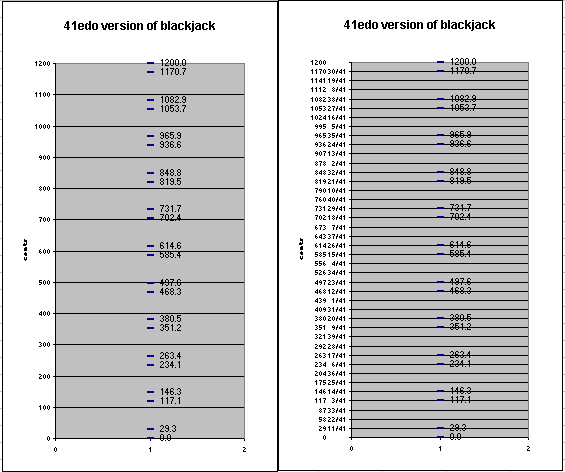
In the 41edo version of blackjack, L is 3 degrees of 41edo and s is 1 degree, so L = 3s.
Links to audio-files of pieces composed in blackjack:
(search the Yahoo Tuning List archives for further background info)
updated:
2001.05.12
2001.05.29
2001.06.11
2001.07.26 -- included corrections from Paul Erlich
2002.02.08 -- changed decimal notation to conform to Graham Breed's symbols
2002.10.23 -- fixed error on decimal notation example (467 cents recta 433), added Breed-pump lattices, applet, and chord-list
2002.11.01 -- added data and lattice for 31edo blackjack
2003.02.10 -- added pitch-height graphs of 31edo and 41edo versions
2003.07.02 -- amended opening paragraphs to include Dave Keenan's more accurate data
2004.08.27 -- ties added to scores of Graham's "comma pump" (thanks to Paul Erlich for suggestion), several links corrected
2007.02.10 -- corrected one typo and reformatted some of the opening paragraphs