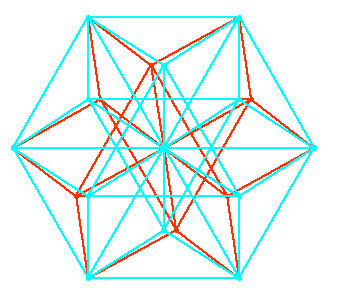
1. The 17 Prime-Limit Tonality Diamond with ratios of 9 and 15 included.

Powers of 3 are plotted on the horizontal axis, powers of 5 on the vertical, powers of 7 on an oblique axis 30 degrees to the horizontal, powers of 11 on a 120 degree axis, powers of 13 at 60 degrees, and powers of 17 at 150 degrees. Although there may be some coincidences when large scales are plotted, for small numbers of tones, this type of rectilinear display is useful as well as visually striking. The axes are color-coded with red assigned to 3, green to 5, blue to 7, yellow to 11, magenta to 13 and cyan to 17. The scale has 65 members and consists of 9 otonal (or major, harmonic) enneads 1 3 5 7 9 11 13 15 17 on the tones of the corresponding utonal (minor or subharmonic) chords.

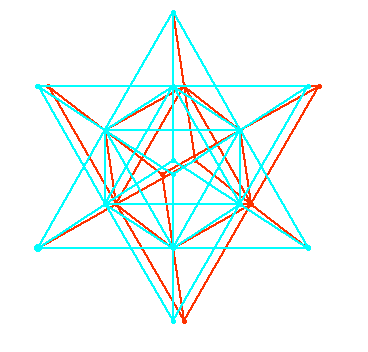
2. The 13 Prime-limit Tonality Diamond with ratios of 9 included.

This 41-tone set of ratios is a subset of the larger scale above. In this projection, the 7's axis is at 30 degrees, 11's at 135 and 13's at 60 to the horizontal. The black background was added for contrast.

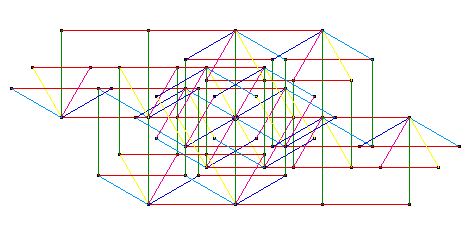
3. Red Triangular Graph.

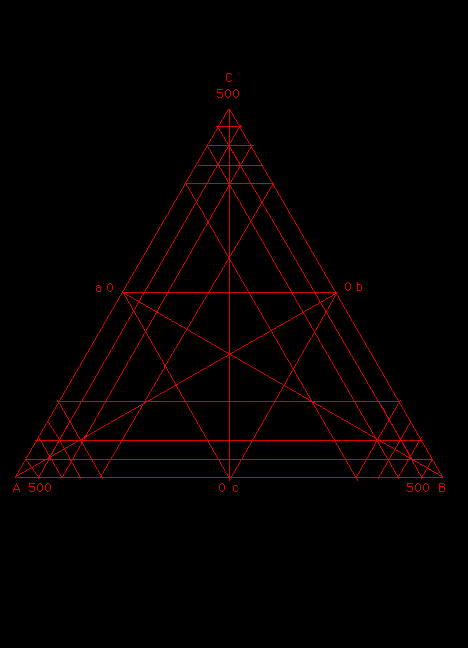
This diagram represents tetrachordal space and was borrowed from physical chemistry where such plots are commonly used depict three component mixtures. Because the mole fractions or percentages must add up to 1 or 100%, there are only two degrees of freedom, thus permitting a planar display. The three 120 degree axes are the sizes of the three intervals (A, B, and C ) comprising the tetrachord, a perfect fourth divided into three subintervals. For convenience, this fourth is taken as 500 cents, the 12-tet value. Because each interval (A, B, or C) is allowed to vary from 0 to 500 cents, all possible tetrachords in all their arrangements or permutations are shown.

This diagram is on the cover of my book, Divisions of the Tetrachord. The musical meaning of the principal zones defined by the web of red lines is described in the next section.

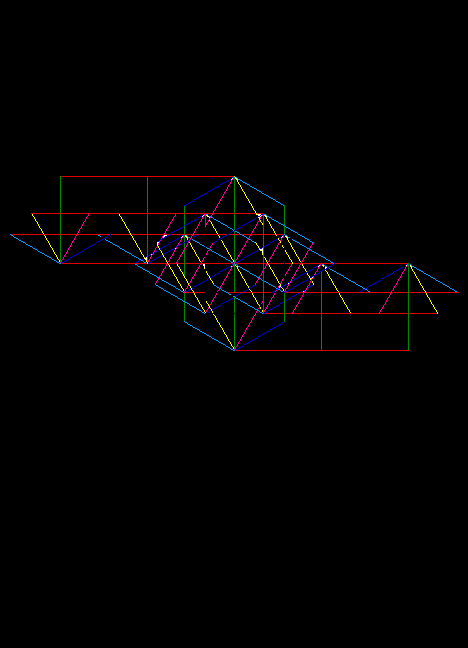
4. Polychrome Triangular Graph.

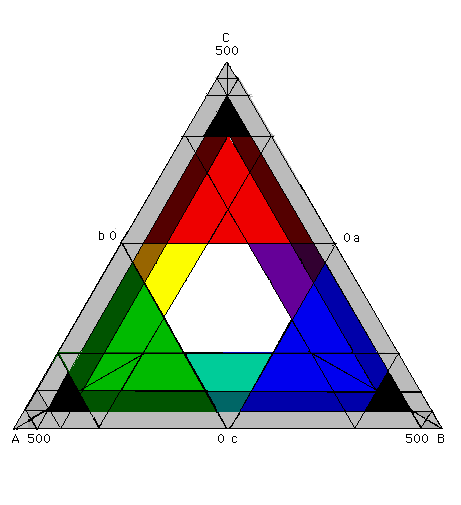
The complete tetrachordal space described in the preceeding paragraph is subdivided into zones defining all possible types of heptatonic scales constructable from 2 identical tetrachords and a disjunctive tone. The central white semi-regular hexagon consists of "strictly proper" diatonic scales (Rothenberg, 1978). The center point represents the division of the fourth into 3 equal parts (approximately 166 + 166 +167 cents) and the six vertices of the figure to the six permutations of Aristoxenos's Soft Diatonic genus (100 + 150 + 250) cents. These six scales and all those which fall on the edges of the region are "proper."

The small trapezoidal regions flanking the central hexagon are "improper" diatonic genera containing intervals smaller than a semitone and larger than a whole tone, that is, mixtures of diatonic with chromatic and enharmonic intervals (such as in Archytas's Diatonic, 28/27 x 8/7 x 9/8 or Aristoxenos's 1/3 + 1 1/6 and 1 tones).

The large triangular regions colored red, green and blue correspond to chromatic genera, in which the sum of the two smaller intervals is less than the third and largest interval. The largest intervals of chromatic genera range from about 250 to around 367 cents, and the smaller intervals sum to between 133 and 250 cents. As the largest interval may lie at the bottom, middle, or top of the tetrachord, three regions are necessary to depict all the permutations.

Beyond the chromatic regions lie the enharmonic, shown here in black. Enharmonic genera consist of a large interval whose size is roughly a major third and two microtones. The small darker regions flanking the chromatic and diatonic zones are chromatic and diatonic genera containing microtones.

Enharmonic genera containing extremely large intervals such as 9/7 or 13/10 have been termed "Hyperenharmonic" by Wilson. Genera containing the extremely small residual microtones of such genera flank all regions.