by Paul Erlich
From the Mills College Tuning Digest
Another duplication of this text, with extensive additional
commentary by me based on conversation with Paul, is available
here
From: Paul Erlich
To: Tuning Digest
[posted to the Tuning Digest since September of 1997]
I do believe that the place and periodicity mechanisms are both at play. I also believe that Plomp's model gives a fine account of the place-related component of dissonance, which I like to call roughness. Combination tones complicate the matter but with a knowledge of the amplitudes and frequencies of all combination tone components, Plomp's algorithm can be still applied. But a phenomenon called "virtual pitch" or "fundamental tracking" is central to Parncutt's treatment of dissonance and does represent, I believe, an additional factor besides critical band roughness. This phenomenon is clearly distinct from the combination tone phenomenon, but it may have a lot to do with periodicity mechanisms. There is a very strong propensity for the ear to try to fit what it hears into one or a small number of harmonic series, and the fundamentals of these series, even if not physically present, are either heard outright, or provide a more subtle sense of overall pitch known to musicians as the "root". As a component of consonance, the ease with which the ear/brain system can resolve the fundamental is known as "tonalness." I have proposed a concept called "relative harmonic entropy" to model this component of dissonance. The harmonic entropy is based on the concept that the critical band represents a certain degree of uncertainty in the perception of pitch, and for any "true" interval, the auditory system will perceive a range of intervals spanning a number of simple-integer ratios. Simple-integer ratios come into the picture because if the heard tones are to be understood as harmonic overtones of some missing fundamental or root, they must form a simple-integer ratio with one another. The range is a sort of probability distribution, and a certain amount of probability is associated with each of the simple-integer ratios.
One way of modeling this is with a Farey series and its mediants. The Farey series of order n is simply the set all the ratios of numbers not exceeding n, and the mediant between two consecutive fractions in a Farey series is the sum of the numerators over the sum of the denominators (this definition has many mathematical and acoustical justifications). The simpler-integer ratios take up a lot of room, defined as the interval between the mediant below and the mediant above, in interval space, and so are associated with large "slices" of the probability distribution, while the more complex ratios are more crowded and therefore are associated with smaller "slices." Now the harmonic entropy is defined, just like in information theory, as the sum over all ratios of a certain function of the probability associated with that ratio. The function is x*log(x). (See an information theory text to find out why.) When the true interval is near a simple-integer ratio, there will be one large probability and many much smaller ones. When the true interval is far from any simple-integer ratios, many more complex ratios will all have roughly equal probabilities. The entropy function will come out quite small in the former case, and quite large in the latter case. In the case of 700 cents, 3/2 will have far more probabilty than any other ratio, and the harmonic entropy is nearly minimal. In the case of 300 cents, 6/5 will have the largest probability in most cases, but 7/6, 13/11, and 19/16 will all have non-negligible amounts of probability, so the harmonic entropy is moderate. In the case of 100 cents, 15/14, 16/15, 17/16, 18/17, 19/18, 20/19, and 1/1 will all have significant probability, and the harmonic entropy is nearly maximal.
In terms of the periodicity model, we can imagine a process which samples the signal for random periods of time (with some probability distribution that is large for very short times and vanishes for long enough times) and in each period, counts the cycles of each pitch to come up with a ratio (or equivalently, to come up with a fundamental frequency, of which the heard note will be harmonic overtones and therefore possess a small-integer ratio by implication). Note that harmonic partials within the heard tones are irrelevant because the cycles here need not be sinusoidal for the counting to occur.
If logs to the base 2 are used in the definition above, the entropy measures the expected amount of information, in bits, needed in an optimal code to communicate the ratio being heard. So the entropy really measures, in a sense, "cognitive dissonance." Now the exact probability distribution of sampling times, or the order of Farey series one should use, is something that may be difficult to determine. However, as the order of the Farey series is increased more and more, the entropy curve (defined as a function of interval width) continues rising but stops changing shape (I have observed this numerically but not proved it mathematically). In the limit of a Farey series of order infinity, one should find a smooth "relative entropy" curve that gives a good approximation of the ups and downs of the entropy curve for any reasonably large finite order. These curves look remarkably like many of the Helmholtz/Plomp curves that were derived from completely different assumptions, and though they are meant to represent a completely different component of dissonance, they lead to the same conclusions for intervals of tones with some appropriate overtone structure.
However, when three or more notes are involved, the two components of dissonance can have quite different behavior. Consider Partch's "otonal" and "utonal" chords. Adding higher identities to both chords increases the roughness of both by the same amount. But while the periodicity of the otonal chords will be unchanged or perhaps multiplied by small powers of two, the periodicity of the utonal chords increases dramatically. Thus the process of counting will not be significantly complicated, and may even be aided, by adding higher identities to the otonal chords, while in the utonal case the likelihood of counting the same relative numbers of cycles in each sampling period becomes very small, and thus the entropy becomes very large. So the high-limit utonal chords, though just as much minima of roughness as the corresponding otonal chords, are almost impossible to assign a fundamental frequency to and are therefore not minima of harmonic entropy.
It is often possible for the brain to look for periodicities among some components of the signal and dismiss the rest as "noise." This is why the root of a major triad does not appear to change when the third is decreased from 5/4 through 11/9 to 6/5 and the chord becomes a minor triad; although the minor triad can be understood as 10:12:15, these numbers are already too high for the entropy of the entire signal to be low enough to compete with the low entropy of the perfect fifth alone (10:15 = 2:3); even the major third alone (12:15 = 4:5) is stronger and can dominate if the "third" is in the bass. In the otonal case, looking at any subset of the notes present (except 9:3, etc.) will lead to a periodicity which is octave-equivalent to, if not identical to, that of the entire chord, so various combinations of components of the signal effect a reinforcement of the tonalness of the overall chord. How to weigh the various subsets' contributions to the probabilities of particular fundamentals in an overall analysis is unclear. Even without the consideration of subsets, there appears to be no mathematical theory of ratios of three of more numbers analogous to Farey theory, and no easy way to create one. Unlike roughness, tonalness is not merely concerned with pairwise interactions of tones but three-way and higher interactions as well. A mathematical model for it is out of my grasp at the moment.
I think it is fair to say that Harry Partch's Genesis of a Music, for all its inconsistencies, forms a common grounding for a great many of us on this list in our discussions. By the way, I intend to model Partch's "one-footed bride" with a sort of octave-equivalent harmonic entropy function; that is, rather than using a Farey series (or a series such as used by Mann where the sum of numerator and denominator does not exceed a certain limit), using instead the ratios up to a given Partch limit ("odd limit", that is, the largest odd factor of either the numerator or denominator does not exceed a certain limit). Instead of letting the order of the Farey series approach infinity, I will let the odd limit approach infinity, and I expect that for some realistic assumption about pitch resolution, the one-footed bride will emerge.
When I worked out a model for harmonic entropy, which should also describe critical band roughness if the partials decrease in amplitude in some specific fashion, I derived that to a good approximation, the complexity of a just ratio is directly related to its DENOMINATOR. Later, imposing octave equivalence made me change this to ODD LIMIT, but I admit that it's possible that octave equivalence does not really come in to the "objective" dissonance of an interval.
A while back I posted on my concept of harmonic entropy. In February 1997 I ran a computer program to compute the harmonic entropy of all intervals within the octave in 1-cent increments, based on the assumption that our brain can ideally recognize ratios with numerator up to N but our hearing of frequencies is blurred in the form of a normal distribution with standard deviation 1% (based on Goldstein's work). I hadn't looked at the results yet, so as a preliminary study I listed the local minima and maxima below.
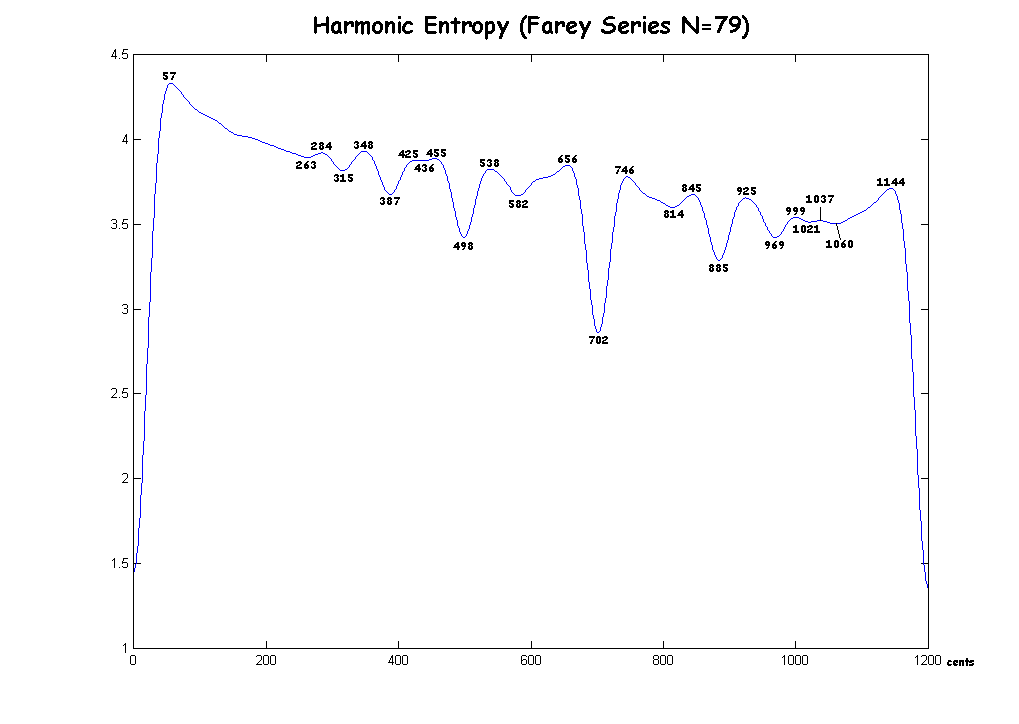
Note that the minima appear to approach the just values as N increases, but the number of minima remains approximately constant. Note also that there is a definite maximum at around 348 cents. This means that harmonically, the brain interprets the neutral third with a variety of ratios, none of which is predominant enough to allow the brain to make a decision. As Johnny Reinhard said, a sort of neutral zone. Other neutral zones appear to be stabilizing for N=80 at around 285 cents, 423 cents (giving the 9/7 a very narrow range of acceptable flattening!), 457 cents, and 537 cents.
The local minima and maxima were as follows (maxima denoted with *):
N=80:
*57
264 (7/6=267)
*285
316 (6/5=316)
*348
387 (5/4=386)
*423
437 (9/7=435)
*457
498 (4/3=498)
*537
581 (7/5=583)
*615
620 (10/7=617)
*656
702 (3/2=702)
*746
814 (8/5=814)
*845
885 (5/3=884)
*924
970 (7/4=969)
*999
1021 (9/5=1018)
*1041
1051 (11/6=1049)
*1145
N=40:
*72
219 (8/7=231)
*242
272 (7/6=267)
*286
314 (6/5=316)
*348
386 (5/4=386)
*426
433 (9/7=435)
*454
498 (4/3=498)
*543
586 (7/5=587)
*654
703 (3/2=702)
*752
811 (8/5=814)
*843
884 (5/3=884)
*923
968 (7/4=969)
*996
1021 (9/5=1018)
*1130
N=20:
*110
171 (11/10=165)
*197
255 (7/6=267)
*287
319 (6/5=316)
*346
384 (5/4=386)
*421
439 (9/7=435)
*450
497 (4/3=498)
*545
585 (7/5=583)
*643
701 (3/2=702)
*761
818 (8/5=814)
*844
885 (5/3=884)
*933
972 (7/4=969)
*1042
1057 (11/6=1049)
*1096
N=10:
*201
270 (7/6=267)
*285
318 (6/5=316)
*347
382 (5/4=386)
*428
436 (9/7=435)
*444
503 (4/3=498)
*552
577 (7/5=583)
*619
710 (3/2=702)
*783
812 (8/5=814)
*840
887 (5/3=884)
*933
965 (7/4=969)
*997
1023 (9/5=1018)
*1049
(remember that for N=10, ratios of 11 aren't even considered)
Here is a graph for the maxima and minima of Farey Series N=79, with maxima and minima labelled:
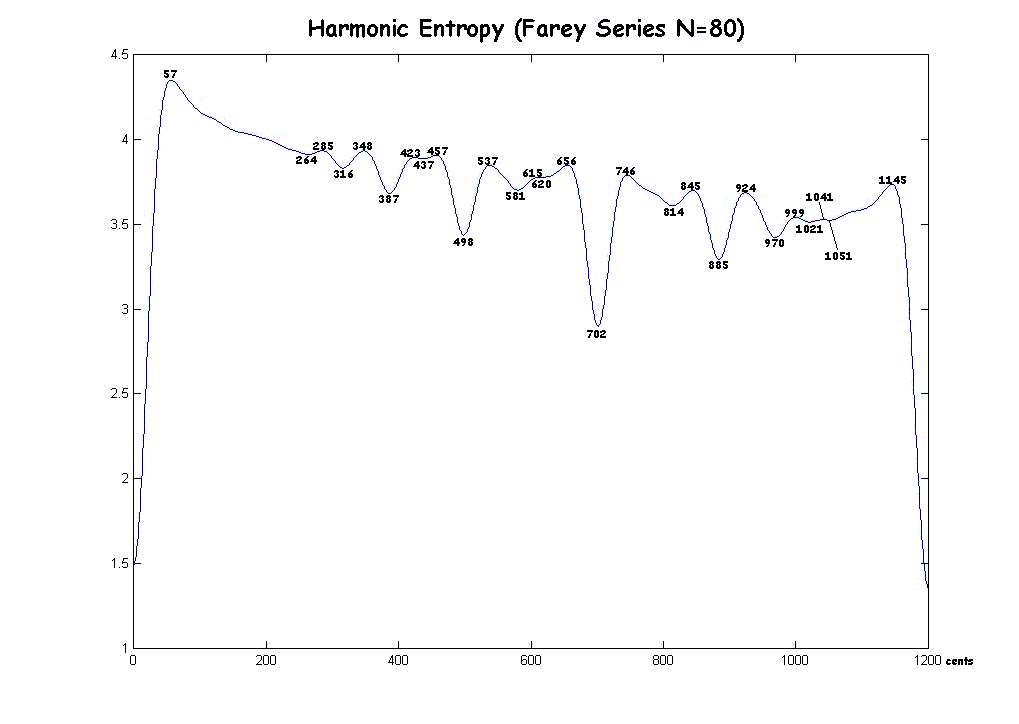
Here is a graph for the Farey Series N=80:
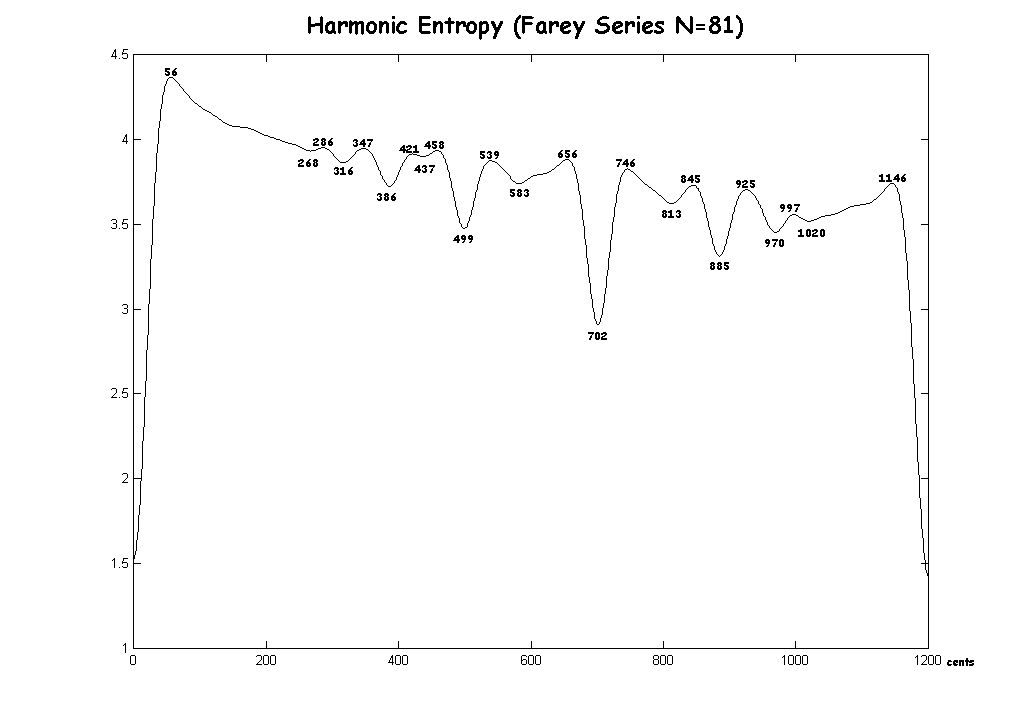
Here is a graph for the Farey Series N=81:
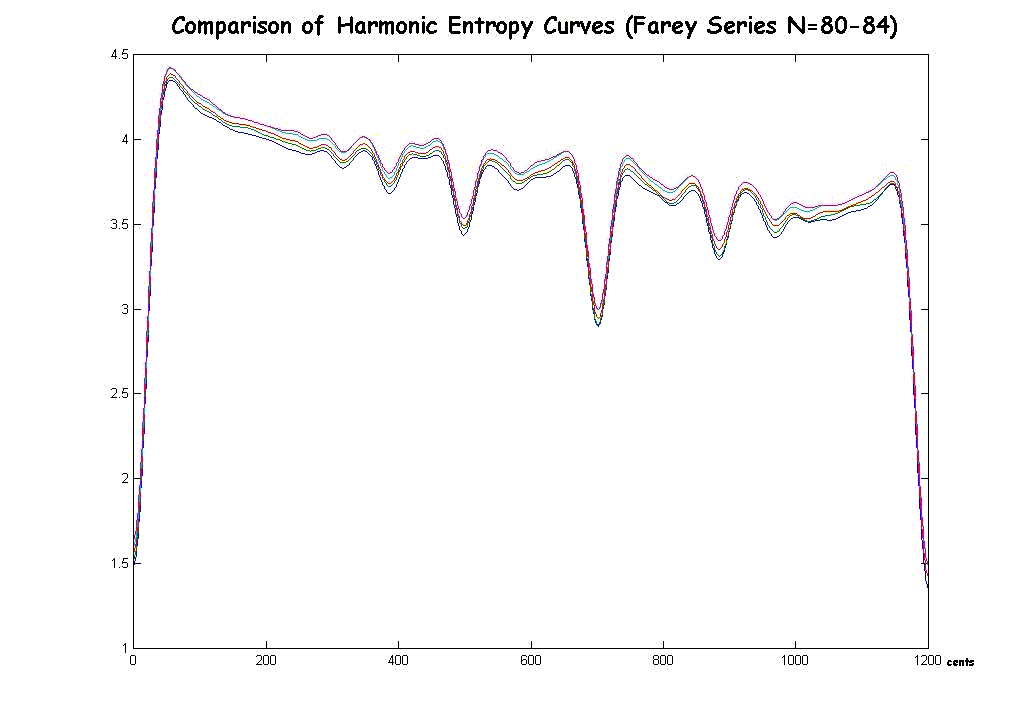
Here is a graph for the six consecutive Farey Series N=79 to 84:
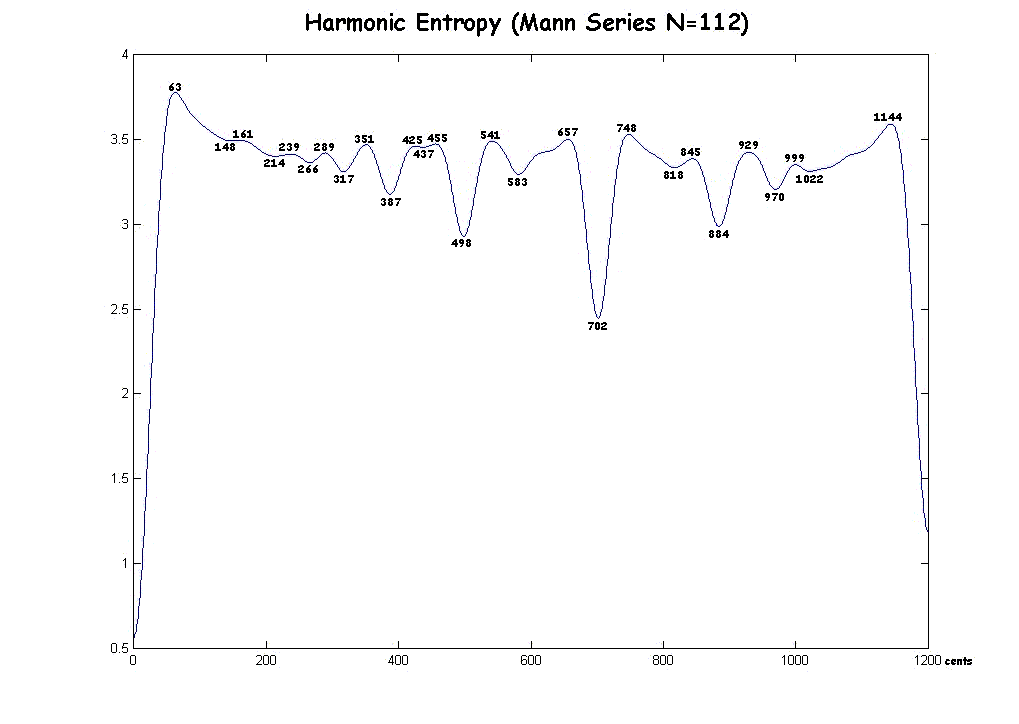
Here is a graph for the Mann Series N=112, with the extrema labelled:
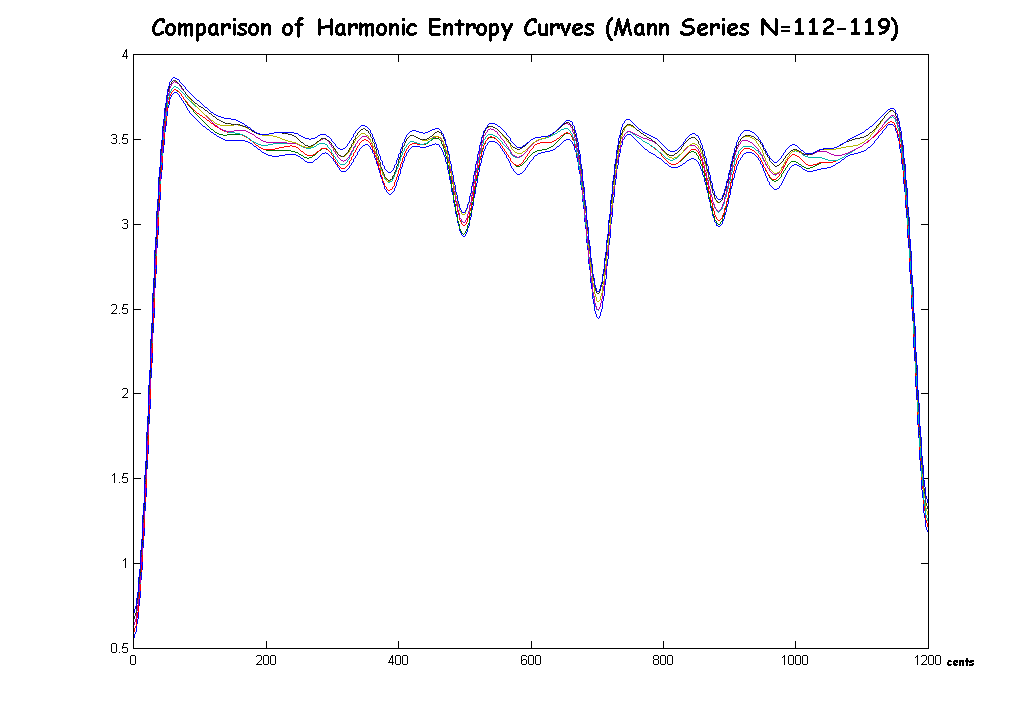
Comparison of Mann Series entropy curves as N increases:
The most important thing I left out was that local maxima and minima have limited relevance unless your music uses continuous sweeps of the interval spectrum. I have always held this as a (very mild) criticism of some of Sethares's arguments. It only takes a tiny change in the harmonic entropy function (say, a change of 1 in N) to convert a local maximum into a local minimum or vice versa. The value of the function need change only very little at any given interval, but the just ratios will tend to be near these local extrema. The values of the function are more important, however these are dependent on whether the allowed fractions in the analysis are defined to have numerator less than N, denominator less than N, num. + den. < 2N, etc. The choice of one of these rules is a difficult one, but the local extrema, I think, should be independent of this choice, which is why I only reported those.
|
or try some definitions. |
I welcome
feedback about this webpage:
|