a visual representation of the mathematical relationships of musical ratios in 2-, 3-, or multi-dimensional space, consisting of points which represent the ratios as positions calculated according to the Fundamental Theorem of Arithmetic.
Lattices may be based upon two types of factoring: either odd or prime - similar to the two types of limit. In either case, a vector is drawn or imagined to represent each factor, with exponents represented as a series of points at regular equal distances along that vector.
Angles between and lengths of the vectors are not standardized; simple triangular or rectilinear lattices are popular for ASCII text use in emails and internet discussion groups. I use a more complex formula of the rectilinear type which provides a unique angle and vector-segment-length for each prime axis.
Here is a simple 2-dimensional example of a 5-limit lattice:
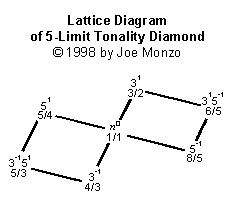
And here is a more complex 4-dimensional diagram:
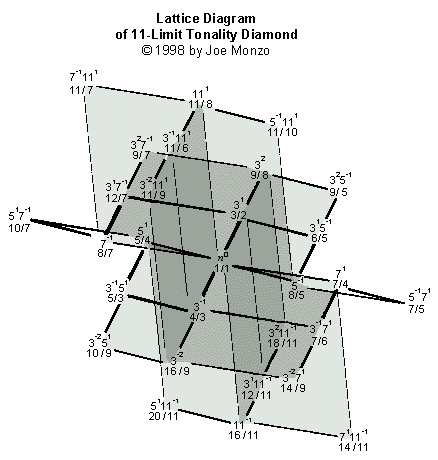
In my theoretical usage, lattices are a graphical expression of my own theory of sonance.
The concept of the lattice arrangement stems from the work of Euler. The precursors to musical lattice diagrams are the Lambdoma, Ellis's Duodenarium and Riemann's Tonnetz matrix charts, which were first used to demonstrate microtonal pitch-relationships by Shohé Tanaka [hmmm ... i'm getting an error from this link now -Monzo]. Harry Partch's Tonality Diamond is related but slightly different.
Adrian Fokker apparently designed the first 3-dimensional lattices with factors of 3, 5, and 7 represented.
John Chalmers has made very complex diagrams of triangles representing tetrachords, following similar principles (see his book Divisions of the Tetrachord and this webpage.)
Probably the most complex diagrams have been designed by Erv Wilson, many of whose hand-drawn lattices form beautiful mandala-like designs (see articles in several issues of Xenharmonikon, reproduced at The Wilson Archives).
Other theorists known for their lattice diagrams are Ben Johnston, David Canright, Graham Breed, Paul Erlich, Dave Keenan, Kees van Prooijen, Paul Hahn, and myself.
[from Joe Monzo, JustMusic: A New Harmony]
I think we should call the various lattice diagrams "tonal lattices", to distinguish them from the partially ordered sets, subject to certain requirements of greatest lower and least upper bounds on pairs of elements, that other mathematicians call lattices.
[from John Chalmers, personal communication]
from a response i made on the
Yahoo
tuning group, which i think helps explain the mathematics
of tuning lattices a little better:
> From: Mark Gould
> To: tuning@yahoogroups.com
> Sent: Tuesday, February 19, 2002 12:23 AM
> Subject: [tuning] Lattices
>
>
> I read the posts about lattices. I usually don't write
> lattices with 3:2 lying along one axis, instead I choose
> to write
>
> etc etc etc
> 36/25-9/5 - 9/8 etc
> | | |
> 6/5 - 3/2 - 15/8 etc
> | | |
> 1/1 - 5/4 - 25/16 etc
> | | |
> 5/3 -25/24-125/96 etc
that's essentially the same as the "triangular" lattices we
draw here ... you're just not drawing lines to connect the
3/2s, but the 3/2s on your lattice d o form a linear axis.
i use either rectangular or triangular lattices. my lattice
formula, which creates the graphics on my webpages, creates a
form of rectangular lattice. but usually when i post something
here i adopt the triangular format which is kind of a standard
for email.
prime-factoring your lattice, the exponents of [3 5] gives you:
[ 2 -2]--[ 2 -1]--[ 2 0]
[ 1 -1]--[ 1 0]--[ 1 1]
[ 0 0]--[ 0 1]--[ 0 2]
[-1 1]--[-1 2]--[-1 3]
the simplest email version of my rectangular lattice,
as well as the format i use in my Excel spreadsheets, as at
http://www.ixpres.com/interval/dict/eqtemp.htm,
follows the [3 5] pattern:
[-1 1]--[ 0 1]--[ 1 1]
[-1 0]--[ 0 0]--[ 1 0]
[-1 -1]--[ 0 -1]--[ 1 -1] etc.
or in simplest terms:
[ 0 +1]
[-1 0]--[ 0 0]--[+1 0]
[ 0 -1]
exponents of 3 increase/decrease along the horizontal axis,
and exponents of 5 increase/decrease along the vertical.
so in my rectangular format the notes in your lattice would go:
[-1 3]
[-1 2]--[ 0 2]
[-1 1]--[ 0 1]--[ 1 1]
[ 0 0]--[ 1 0]--[ 2 0]
[ 1 -1]--[ 2 -1]
[ 2 -2]
the ratio lattice of that would be:
125/96
|
25/24 -- 25/16
| |
5/3 -- 5/4 -- 15/8
| |
1/1 -- 3/2 -- 9/8
| |
6/5 -- 9/5
|
36/25
the triangular format simply skews that a bit
so that the basic 5-limit concords, 6/5 and 5/4,
are like mirror-images of each other with reference
to the 1/1; here's the [3 5] pattern:
[-1 1] -- [ 0 1] -- [ 1 1]
/ \ / \ /
[-1 0] -- [ 0 0] -- [ 1 0]
/ \ / \ /
[-1 -1] -- [ 0 -1] -- [ 1 -1] etc.
or in simplest terms:
[ 0 +1]
/
[-1 0] -- [ 0 0] -- [+1 0]
/
[ 0 -1]
so the typical "triangular" version of your lattice is:
[-1 3]
/ \
[-1 2] -- [ 0 2]
/ \ / \
[-1 1] -- [ 0 1] -- [ 1 1]
\ / \ / \
[ 0 0] -- [ 1 0] -- [ 2 0]
\ / \ /
[ 1 -1] -- [ 2 -1]
\ /
[ 2 -2]
and in ratios (we usually use : instead of /
to avoid confusion with the connecting lines)
125:96
/ \
/ \
25:24--25:16
/ \ / \
/ \ / \
5:3---5:4---15:8
\ / \ / \
\ / \ / \
1:1---3:2---9:8
\ / \ /
\ / \ /
6:5---9:5
\ /
\ /
36:25
it should be easy to see that all three of these formats
are transformations of each other.
Updated: 2002.2.19, 2002.1.8