Diesis is a term which has been used so variously at different times in history that it requires 6 separate definitions here.
When the term is unqualified, it generally is meant to refer to the ratio 128:125 = [2 3 5]^[7 0 -3] = ~41.05885841 (~411/17) cents, as described in definition #4 below.
1.
The historically prior usage of this term is by
Philolaus (fl. c. 400 BC), as quoted by Boethius,
to refer to the interval that is normally known as a
limma
or Pythagorean minor semitone, with the ratio
256:243 = ~90.22 cents.
2. A variety of intervals smaller than the
limma were called diesis in ancient Greek theory, including
the so-called 'quarter-tones' of
Aristoxenus.
The term was revived in medieval Europe when the
ancient Greek treatises became known and were translated into
Latin. There was no one specific measurement, but the
values clustered approximately around 50
cents.
3. The infamous "fifth-tones" of
Marchetto
of Padua were named by him "dieses". According
to my analysis, Marchetto's dieses were of five different
sizes: approximately 22, 44, 45, 46, and 47 cents.
The group of the four larger ones are best viewed as variants of one generic size, so that we may say my interpretation of Marchetto's dieses posits two basic sizes, ~22 cents and ~44-47 cents.
This usage has a modern counterpart in the 31-eq [or 31-ET] system, in which the (slightly-smaller-than-)"fifth-tone" was named diesis by Fokker. This interval is 2(1/31) [= 0.39 Semitone = ~38.710 cents]. The formula for calculating the diesis-value (as used in this definition) of any ratio is:
dieses = log10(ratio) * [31 / log10(2)]
4. This term is also used with a qualifying adjective
to designate several specific 5-limit intervals.
Together, Rameau and Ellis named three dieses, but not in
a consistent manner. The two named by Rameau were called
"major" and "minor diesis". Ellis confusingly
called Rameau's "minor diesis" by the name "great diesis",
and chose another interval altogether as his "small diesis".
The two named in Ellis's chart [see p 453 of his translation of Helmholtz, On the Sensations of Tone] are the
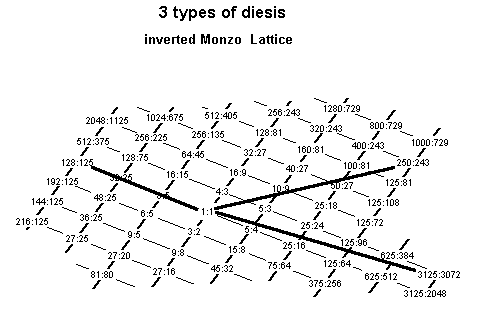
Small Diesis with a ratio of 3072:3125 = 2-103-155 = 0.29 Semitone = ~29.614 cents, and theGreat Diesis with a ratio of 125:128 = 275-3 = 0.41 Semitone = ~41.059 cents.
Rameau:
also named 125:128, calling it the Minor Diesis, and his other diesis was theMajor Diesis with a ratio of 243:250 = 213-553 = 0.49 Semitone = ~49.16613727 cents.
In 5-limit
intervals, 100 cents and under, I suggested calling these,
respectively, the "super-pentapental", "sub-tripental",
and "super-tripental diesis". These names describe precisely
the power of prime-factor 5 for each of these ratios.
Below is a Monzo
lattice illustrating the
prime-factorization of these three types of dieses:
5. I also use the term "diesis" with a qualifier, to
indicate any interval of approximately 40 to 70 cents.
For example, the "undecimal diesis" has the ratio 33:32 and is ~53.27294323 cents, and indicates the intonational difference represented by the accidental ^ in my use of 72-EDO to accompany my JustMusic Prime-Factor Notation (AKA "HEWM notation) in notating the pitches F : F^.
Another example of a commonly-encountered ratio in this range is the "septimal" diesis, ratio 36:35 = ~48.7703814 cents. The intonational difference indicated by this diesis may be notated in HEWM with either the simplified form, which is the same ^ as above, or by the more complicated combination >+ which follows the ratios logically.
6.
The
"s" (= smaller of the two
step-sizes) in the
blackjack scale
is another type of diesis. In the typical
72-EDO tuning of blackjack, this
interval is 2(2/72) = 331/3 cents.
see also anomaly, comma, kleisma, skhisma, 5-limit intervals, 100 cents and under
[from Joe Monzo, JustMusic: A New Harmony]
Updated: 2002.2.16, 2002.1.27