- 1. The historically prior usage of this term is by Philolaus (fl. c. 400 BC), as quoted by Boethius, to refer to an interval that is considerably larger than the schisma we normally mean today.
- 2. In its usual modern sense, a term coined by Alexander Ellis in his translation of Helmholtz's On the Sensations of Tone, and originally spelled skhisma. It designates an extremely small interval, just barely discernible to human pitch-detection.
- 3. As no combination of different prime numbers will ever produce ratios which have exactly the same interval size, if cycles of a particular ratio are calculated far enough, very small intervals like this eventually appear between ratios having different sets of prime factors. When these are under consideration, the term schisma is qualified with a latin word designating the higher prime, with the assumption that the other prime being compared is a more familiar one, almost always 3.
Philolaus described the schisma as an integral 1/2 of the comma (which today we call the Pythagorean comma):
Philolaus's schisma = comma(1/2)
= (2-19 * 312)(1/2)
= 2-(19/2) * 36
= ~11.73 cents.
Unqualified, it is the difference between the
51
just
"major 3rd"
and the 3-8
Pythagorean
"diminished 4th", and has an interval size of approximately
1/50
Semitone [= ~ 2 cents]:
prime-factor vector ratio Semitones ~cents
2 3 5
[ -2 0 1] 5/4 3.86 386.3137139 just "major 3rd"
- [ 13 -8 0] 8192/6561 3.84 384.3599931 Pythagorean "diminished 4th"
-------------
[-15 8 1] 32805/32768 0.02 1.953720788 skhisma
The skhisma may also be found as the difference between the
Pythagorean comma
and the
syntonic comma:
prime-factor vector ratio Semitones ~cents
2 3 5
[-19 12 0] 531441/524288 0.235 23.46001038 Pythagorean comma
- [ -4 4 -1] 81/80 0.215 21.5062896 syntonic comma
-------------
[-15 8 1] 32805/32768 0.02 1.953720788 skhisma
Below is a Monzo lattice illustrating the [3 5] prime-factorization of the skhisma:
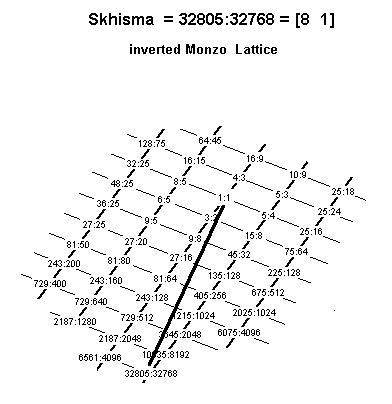
Note that the skhisma is nearly the same size as the
grad,
the difference between them being only ~0.001280077
(= ~1/781) cent:
2^x 3^y 5^z
[ -19/12 1 0 ] grad
- [ -15 8 1 ] skhisma
----------------------
[ 161/12 -7 -1 ] difference between grad and skhisma
Thus, we get the septimal schisma,
which is the difference between the
3-14 Pythagorean
"doubly diminished 8ve" and the
71 harmonic "minor 7th",
and has an interval size of approximately
1/26 Semitone:
prime-factor vector ratio Semitones ~cents
2 3 7
[23 -14 0] 8388608/4782969 9.73 972.6299879 Pythagorean "doubly diminished 8ve"
- [-2 0 1] 7/4 9.69 968.8259065 harmonic "minor 7th"
--------------
[25 -14 -1] 33554432/33480783 0.04 3.804081415 septimal skhisma
Likewise, there is the nondecimal schisma, which is the difference between
the 191 harmonic "augmented 2nd"
and the 'standard' 3-3
Pythagorean
"minor 3rd",
and which has an interval size of approximately
1/30 Semitone:
prime-factor vector ratio Semitones ~cents
2 3 19
[-4 0 1] 19/16 2.98 297.5130161 harmonic "augmented 2nd"
- [ 5 -3 0] 32/27 2.94 294.1349974 Pythagorean "minor 3rd"
---------------
[-9 3 1] 513/512 0.04 3.378018728 nondecimal skhisma
Schismas are a key element in my concept of bridging.
I refer to the three schismas explained here as the 3==5, 3==7, and 3==19 bridges,
respectively.
see also:
anomaly
schismic
skhismic major 3rd
comma
kleisma
5-limit intervals,
100 cents and under
[from Joe Monzo, JustMusic: A New Harmony]
Updates:
2002.09.28 -- added vector notation describing commatic derivation, in #2
2002.09.23 - added descriptive interval names and vector addition, numbered #3 as such