- the Whole Tone (9/8, 204 cents [¢]),
- the Ditone (81/64, 408¢),
- the Limma or diatonic semitone (256/243,90¢),
- the Apotome or chromatic semitone (2187/2048, 114¢),
- the Pythagorean Minor Third (32/27, 294¢) and
- the Pythagorean or Ditonic Comma (24¢).
an adjective describing the construction of a scale or musical system by successions of 3/2's (just "perfect fifths")
[from Partch 1974, Genesis
of a Music, 2nd ed., Da Capo Press, New York, p. 75]
When the ratios of pitches in a Pythagorean tuning are
considered as
vectors
of exponents
prime-factor
3, they may be plotted as a 1-dimensional
or linear system, as in the example on this
lattice diagram:
In
JustMusic
terminology, such a system
would be described as a cycle of powers of 3. Pythagoras was
given credit in ancient Greece for discovering the properties
of musical ratio numbers, with an emphasis on what we would
today call powers of 3.
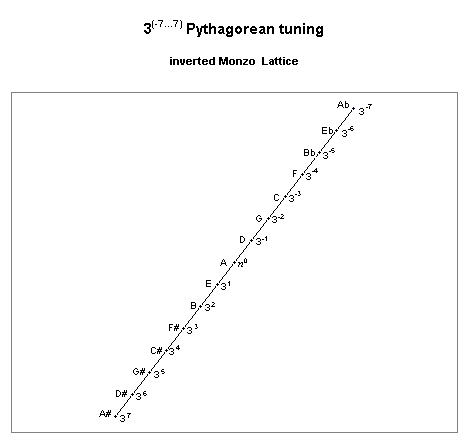
It is easy to see from the lattice that Pythagorean tuning is of the type that may be characterized as a chain.
"A" was deliberately chosen as the central reference pitch here, instead of the "C" which is used nearly universally as the reference today. This is primarily for historical reasons, as the notation of musical pitches with letters and accidentals is based on Pythagorean tuning centered on "A", as can be seen in this lattice.
(As the lattice shows, the true point of symmetry is "D". For this reason, "D" was chosen as the reference n0 by some theorists, such as Fokker. Because the overriding principle in Sumerian art is symmetry, this is also the reason why "D" is the letter-name I use to represent the reference pitch in my speculations on Sumerian tuning.)
The core of the tuning is the 7-tone diatonic scale, indicated on this lattice as the set of pitches from F 3-4 to B 32.
The interval represented as 37 is the chromatic semitone in this tuning, i.e., a distance of 7 steps on the lattice indicates a change from a plain letter-name to one with a sharp or a flat.
Below is an
interval-matrix
of the Pythagorean
diatonic scale, in
cents:

312, or a distance of 12 steps
on the lattice, indicates the
Pythagorean comma,
the basic interval of
enharmonicity
in this tuning. This is the distance on the lattice
between two pitches which are equivalent in the usual
12-EDO scale,
as for example Eb 3-6 and D# 36.
These are two slightly different pitches in Pythagorean
tuning, about 23 & 1/2
cents apart.
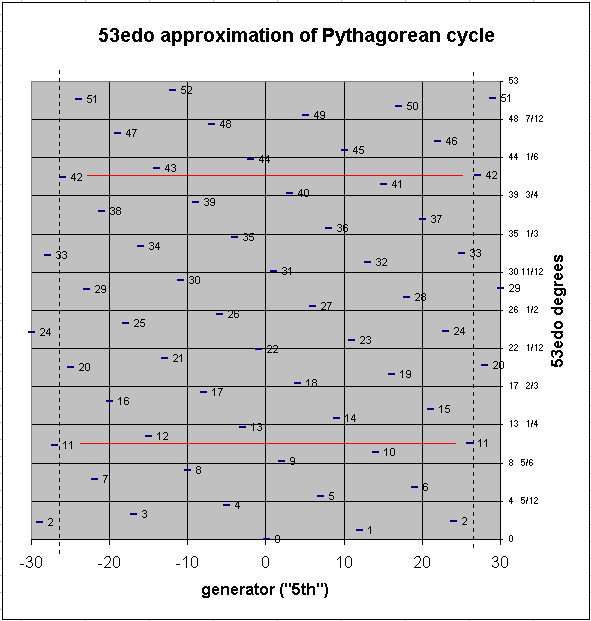
A smaller interval which results from carrying the chain out to 53 degrees is Mercator's comma, 353, which is ~3.615045866 cents, the difference between 4 Pythagorean commas (348) = ~93.84004154 cents and a limma (3-5). Since 4 commas is nearly the same as the limma, and the apotome (37) is one comma larger, this is the origin of the old idea that a "whole-tone" (= limma + apotome) is divided into 4 + 5 = 9 commas. In terms of logarithmic L and s, the "8ve" is composed of 5L + 2s, which equals (5*9)+(2*4) = 45+8 = 53 commas. Thus, the early realization that a 53-tone Pythagorean chain is a nearly-closed system, which would lead to the further realization that 53edo is an excellent approximation of Pythagorean tuning.
The graph below shows the 53edo approximation of a Pythagorean chain with the arbitrary boundaries of 3(-30...+30), showing that Mercator's comma vanishes. The y-axis shows fractional divisions of 53edo degrees because it is divided into 12 equal parts, for comparison to 12edo. The black vertical dashed lines show the arbitrary 3(-26...+26) boundaries of a 53edo cycle centered on n0 (if A=n0, this is Bbbbb...Gxx), and the red horizontal lines show the vanishing of Mercator's comma at either end of the cycle if it is continued beyond those boundaries. Assuming Mercator's comma to be below the "margin of error" in interval perception (usually given as ~5 cents), 53edo thus provides an approximation which is audibly indistinguishable from a 53-tone "pure" Pythagorean chain.
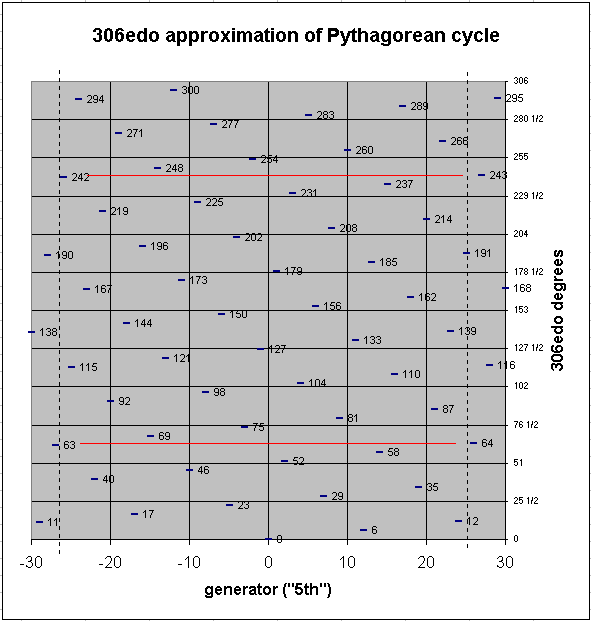
An excellent logarithmic approximation to Pythagorean tuning which does articulate Mercator's comma (probably more useful for analysis than as an actual intonation) is 306edo, where Mercator's comma is 1 degree. Below is the same graph, this time in 306edo, and this time showing Mercator's comma by the red horizontal lines:
The next point at which the Pythagorean chain nearly closes is 3665, an interval dubbed the satanic comma. It is only ~1/13-cent and thus is completely indistinguishable by any ear.
It can also be seen from these graphs that there is another interval the size of a "comma" at 3-41 = ~19.84496452 cents. In 53edo it is 1 degree, identical to the Pythagorean comma; in 306edo it is 5 degrees, one less than the 6 degrees which compose the Pythagorean comma.
Pythagorean tuning can be considered a particular instance of
the schismic family
of temperaments.
[from Joe Monzo,
JustMusic: A New Harmony.
I consider the definitive work on Pythagorean tuning to be
Margo Schulter's
Pythagorean
Tuning and Medieval Polyphony webpages.]
Pertaining to the philosopher Pythagoras.
In tuning theory, Pythagorean refers to a system of tuning by Perfect Fourths, Fifths and Octaves.
Important Pythagorean intervals are:
[from John Chalmers, Divisions of the Tetrachord]
Updated:
2003.02.09 -- added interval matrix
2002.10.29 -- added paragraph about 9 commas per semitone, 53edo graph, revised 306edo graph
2002.10.19 -- added data on 53edo and 306edo
2002.1.12