See Diatonon
[from John Chalmers, Divisions of the Tetrachord]
(The latter is also referred to as a '7oo12' or '7-out-of-12' scale.)
The diatonic semitone is the interval between two notes of a diatonic scale which have different letter-names, whether or not one of them is qualified by an accidental, as in B:C or A:Bb. The implication is that both tones are bonafide diatonic scale-degrees. This interval is called the "minor 2nd" and may be found abbreviated as min2, m2, b2, or -2 . See also chromatic.
In the Pythagorean [3-Limit] system, the diatonic semitone is also called the leimma or limma.
Note that in positive systems (typical example: Pythagorean tuning), the chromatic semitone is larger than the diatonic, while in negative systems (typical example: any meantone tuning) it is exactly the opposite and the diatonic is the larger.
Marchetto specified three types of semitone and called the third, naturally enough, the enharmonic; however, his names were matched with the intervals differently than in traditional theory.
General comments about diatonic scales / semitones
The 5-limit
JI diatonic scale is a
periodicity-block whose
unison-vectors
are the
syntonic comma
and the
chromatic
semitone 25:24.
Here is a Monzo lattice of the most typical version of the
scale in the
major mode:
Unison-vectors:
81:80 = [ 4 -1] syntonic comma
25:24 = [-1 2] Ellis's "small semitone", Rameau's "minor semitone"
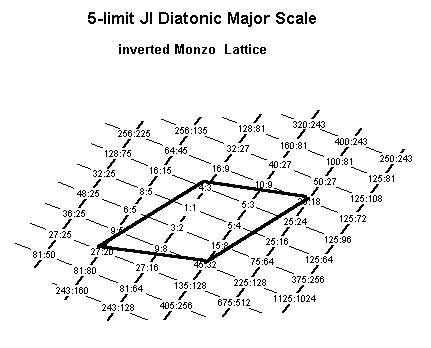
The diatonic semitone in this scale is the ratio 16:15 = 243-15-1 = ~111.7312853 cents. It occurs in this scale between the pairs of ratios ( 5/4 : 4/3 ) and ( 15/8 : 1/1 ) ; if we call the 1/1 "C", this is between E:F and B:C.
By moving the boundaries of the periodicity-block as a group, it may be transposed to other keys or also to the minor mode in various keys, and retain all of its essential properties.
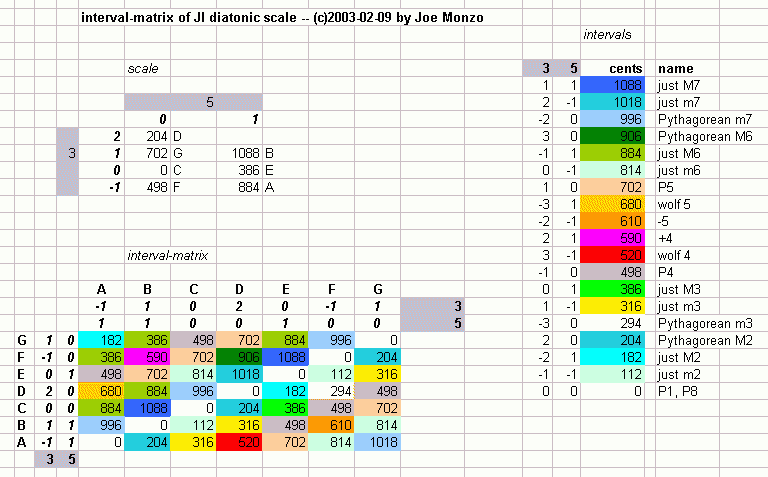
Below is an
interval-matrix
of the
just-intonation
diatonic scale given in the above lattice, in
cents:
If the lattice shown above were to be cut along the top and bottom
(diesis
unison-vector)
boundaries of the
periodicity-block,
extended infinitely,
and then wrapped into a cylinder so that those two edges
meet (i.e, so that 9:8 and 10:9 would occupy the same point,
etc.), and then snipped along the left and right edges
(which are theoretically
infinitely distant)
according to how many pitches are contained in the given system,
this would describe perfectly the harmonic tonal
relationships avialable in the various
meantone tunings,
whose diatonic scales are the basis of the standard
repertoire of "common-practice" (c. 1600-1900) Eurocentric
music and music-theory.
In a meantone tuning, the diatonic semitone is technically
-5 generators.
Here are the sizes of the diatonic semitone in various
historical meantone tunings:
meantone equivalent EDO
~cents ~cents
1/3-comma 126.0688117 2(2/19) 126.3157895
2/7-comma 120.9482665 2(5/50) 120.0
7/26-comma 119.1757701 " "
1/4-comma 117.1078577 2(3/31) 116.1290323
2/9-comma 114.120873 2(7/74) 113.5135135
1/5-comma 111.7312853 2(4/43) 111.627907
1/6-comma 108.1469037 2(5/55) 109.0909091
1/11-comma 100.0005819 ~= 2(7/12) 100.0
Note also that the MIRACLE generator, the secor (~116.7 cents), is also in the typical size range of a diatonic semitone, altho it may not function as one.
See also:
[From Joe Monzo, JustMusic: A New Harmony]
An adjective referring to octave scales consisting of 7 tones and composed at most of three semitones.
Comments:
Classical examples with three different semitones:
- JI major and minor scales
- Helmholtz (= gypsy) major and minor scales
- Redfield major and minor scales
Classical examples with two different semitones:
- Greek modes (in the frame of Pythagorean Tuning)
- scales of the fifth circle in the frame of the 1/4-comma meantone tuning
Classical example with only one semitone:
- heptatonic (e.g. Messien's) modes in the frame of 12-TET
[From Jan Haluska, personal communication]