a system of tuning based on notes whose frequencies have small-integer rational relationships, or relationships which are so close to this that they are audibly indistinguishable from it. Abbreviated as JI.
The scales produced are almost always unequally-spaced, and usually exhibit various types of symmetry. Because of the Fundamental Theorem of Arithmetic, a cycle of 3/2s ["5ths"], or of any other just ratio, will never return exactly to an "octave" of the origin frequency. This is because the "octaves" are powers of prime-factor 2, while all other just ratios have other prime-factors.
There is great debate and a huge variety of opinions among tuning theorists over the exact meaning of the term "just intonation". When unqualified, most writers use "just intonation" to refer to a 5-limit tuning, as described in my paper.
Rational tuning systems with a prime or odd-limit higher than 5 are frequently called extended just intonation (example: Ben Johnston), but many composers who work in higher limits refer to their work also as simply "just intonation" (examples: La Monte Young, Harry Partch, Lou Harrison, Kraig Grady, Kyle Gann, David Doty, Pat Pagano ["shree swifty"], David Beardsley). Many people also refer to ancient Greek tuning systems, which had primes up to 31, as "just intonation".
3-limit rational systems, while also technically "just intonation", are generally called Pythagorean.
References to different authors's varying usage of the term "just intonation" are given at the bottom of this page.
Below is a lattice diagram of an extensive "8ve"-equivalent 5-limit system. It shows the ratios which correspond to exponents of only the prime-factors 3 and 5, thus it is a 2-dimensional or planar system. The lattice theoretically continues infinitely in all four directions, the 3-axis radiating outward from the central 1:1 to the south-west in the positive direction and to the north-east in the negative, and the 5-axis radiating outward from 1:1 to the south-east in the positive direction and to the north-west in the negative.
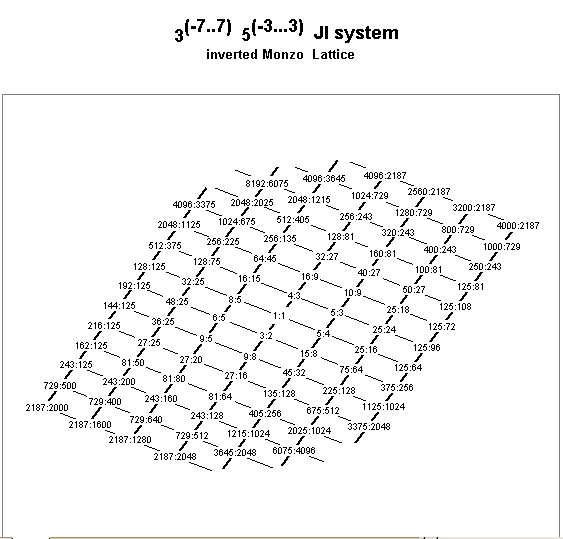
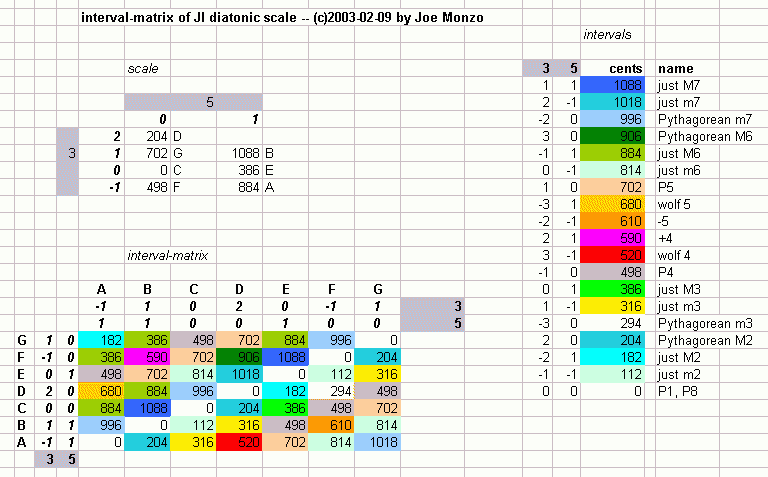
Below is an
interval-matrix
of the most typical example of the JI
diatonic scale, in
cents:
Here is a selection of postings to the Tuning List
which explore the origins of the actual term
"just intonation" (by me unless otherwise noted):
16441
16460
16476
16502 (Margo Schulter)
16524
[from Joe Monzo, JustMusic: A New Harmony]
Any tuning system which exclusively employs intervals defined by ratios of integers may be called Just Intonation, though some authors restrict it to systems whose intervals are derived from the first six overtones, 1, 2, 3, 4, 5, and 6. Such systems are often termed "Five Limit" or "Senary" systems after Zarlino's "senario" (Partch, 1949, 1974, 1979). The most common example of such a system is the tuning of the Major Mode as 1/1 9/8 5/4 4/3 3/2 5/3 15/8 and 2/1.
Just Intonation is contrasted to Equal Temperament and Unequal Temperaments such as Meantone which combine rational with irrational intervals.
[from John Chalmers, Divisions of the Tetrachord]
References citing the term "just intonation"
No prime or odd limit specified
The Shorter Oxford English Dictionary on Historical Principles.
Just
Mus. in just interval, etc. : Harmonically pure; sounding perfectly in
tune. 1811.
[This was quoted in a post by Dave Keenan to the tuning list, message 15836 (Thu Nov 23, 2000 11:39pm), which began a big discussion over the definition of "just intonation".]
Randel, Don Michael, editor.
The New Harvard Dictionary of Music
"just intonation" entry, p 422:
[Fr. intonation juste; Ger. reine Stimmung; It. accordatura giusta; Sp. entonación justa].(1) The beatless tuning of an interval, one that brings it into agreement with some analogous interval in the harmonic series. Such intervals are considered to be acoustically pure. They are expressed by ratios containing the smallest possible integers corresponding to the lowest analogous partials of the harmonic series. When an interval can be expressed by adjacent partials in the series it has the form (x+1):x [i.e., is superparticular or epimoric -Monzo].
(2) Any tuning that incorporates five or more acoustically pure types of interval within the octave; in the case of diatonic or chromatic scales, those based on acoustically pure major thirds and acoustically pure fifths. It is not possible to construct a diatonic scale in which both fifths and thirds are pure. ...
The earliest known theorists to assert the superiority of the just third are Theinred of Dover (12th century) and Walter Odington (fl. 1298-1316), both from England, where early polyphony gives considerable prominence to imperfect consonances such as the third. The earliest theorist to publish a complete just tuning is the Spaniard Bartolomeo Ramos de Pareja (ca. 1440-1491?). Apparent ancient antecedents such as Didymus's diatonic and Ptolemy's diatonic syntonic scales have often been cited since the 17th century but are somewhat illusory. The focus of interest in such ancient Greek tunings was on the dimensions of scale steps within tetrachords. Ratios for thirds and sixths are demonstrably incidental. [See my Tutorial on ancient Greek tetrachord-theory - Monzo] In late medieval accounts of just tunings, on the other hand, the focus is precisely on these two intervals. ...
Bibl.: Adriaan Fokker, Just Intonation (The Hague: Nijhoff, 1949). ... Harry Partch, Genesis of a Music, 2nd ed. enl. (New York: Da Capo Press, 1974).
Schulter, Margo. tuning list message 33254 (Sun Jan 27, 2002 11:20 pm)
(1) Just intonation could be taken as synonymous with rational intonation (RI), the use of integer ratios (simple or complex) to build a complete tuning system;(2) Just intonation could additionally be taken to imply that some intervals, especially those which may be regarded as "fully consonant" or "stable," have _simple_ interval ratios (e.g. 3:2 and 4:3);
(3) Just intonation could be yet further taken to suggest a system featuring or tending toward superparticular or epimore ratios for melodic steps and other types of intervals, as with many Greek tetrachord schemes;
(4) Just intonation could be taken to imply that ratios based on two or more simple primes larger than two are combined in a single system, giving rise to the intricacy and frequent "asymmetry" associated with a "JI" system (other than 3-limit or Pythagorean); and
(5) Most narrowly, but very commonly in a certain perspective centered on composed European music of c. 1480-1900, "JI" could be taken to imply specifically "5-limit JI," where the intervals deemed to be stable concords in the styles of this region and period are pure.
Doty, David, Just Intonation Network webpage What is JUST INTONATION?:
JUST INTONATION is any system of tuning in which all of the intervals can be represented by ratios of whole numbers, with a strongly-implied preference for the smallest numbers compatible with a given musical purpose. Unfortunately this definition, while accurate, doesn't convey much to those who aren't already familiar with the art and science of tuning. The aesthetic experience of just intervals and chords, however, is unmistakable.
The simple-ratio intervals upon which Just Intonation is based are the fundamental constituents of melody and harmony. They are what the human auditory system recognizes as consonance, if it ever has the opportunity to hear them in a musical context. The significance of whole-number ratios has been recognized by musicians around the world for at least 5000 years.
Just Intonation is not a particular scale, nor is it tied to any particular musical style. It is, rather, a set of principles which can be used to create a virtually infinite variety of intervals, scales, and chords which are applicable to any style of tonal music (or even, if you wish, to atonal styles). Just Intonation is not, however, simply a tool for improving the consonance of existing musics; ultimately, it is a method for understanding and navigating through the boundless reaches of the pitch continuum—a method that transcends the musical practices of any particular culture.
Just Intonation has depth and breadth. Its fundamental principles are relatively simple but its ramifications are vast. At present, Just Intonation remains largely unexplored. A few pioneering composers and theorists have sketched in some of its most striking features, but the map still contains many blank spaces where the adventuresome composer many venture in hopes of discovering new musical treasures.
Valentine, Bob, Yahoo tuning group message 33284:
"Historically, it has generally been used in Western music to refer to... ...however, Western Classical music, despite the claims of some theorists, is unplayable in a fixed Just Intonation and therefor is either adapted or tempered".
You could go on and say, "some have adopted a standard whereby ratios of larger integers and/or primes (higher odd limits) are described as rational intonation and those of smaller odd limit are Just Intonation, with the line being drawn at some point whereby a practioner cannot tune the interval by ear."
"Clearly there are points where all these distinctions break down due to the inability of humans pitch and harmonic discrimination. The Hammond organ for instance, is an RI system with an odd limit less than 100, however to most listeners and players, it represents the irrational 12tet system. Similarly (EDO of choice) is an irrational system which can approximate a (limit of choice) JI system with sufficient accuracy as to be virtually indistinguishable."
JI = 5-limit
Helmholtz, Hermann.
On the Sensations of Tone...,
appendix XVII: Plan for Justly-Tuned Instruments with a single manual;
appendix XVIII: Just Intonation in singing.
[Without any comment on the prime-limit, Helmholtz uses the term "just intonation" to refer only to 5-limit systems here.]
Lindley, Mark.
in New Grove's Dictionary of Music and Musicians,
"just intonation" entry
[Note the extensive bibliography at the end of this.]
Just [pure] intonation.
When pitch can be intoned with a modicum of flexibility, the term 'just intonation' refers to the consistent use of harmonic intervals tuned so pure that they do not beat, and of melodic intervals derived from such an arrangement, including more than one size of whole tone. On normal keyboard instruments, however, the term refers to a system of tuning in which some 5ths (often including D--A or else G--D) are left distastefully smaller than pure in order that the other 5ths and most of the 3rds will not beat (it being impossible for all the concords on a normal keyboard instrument to be tuned pure; see Temperaments, 1). The defect of such an arrangement can be mitigated by the use of an elaborate keyboard.
1. General theory.
In theory, each justly intoned interval is represented by a numerical ratio. The larger number in the ratio represents the greater string length on the traditional Monochord and hence the lower pitch; in terms of wave frequencies it represents the higher pitch. The ratio for the octave is 2:1; for the 5th 3:2; for the 4th 4:3. Pythagorean intonation shares these pure intervals with just intonation, but excludes from its ratios any multiples of 5 or any higher prime number, whereas just-intonation theory admits multiples of 5 in order to provide for pure 3rds and 6ths. [Monzo: note that Lindley doesn't say JI excludes anything higher, though the casual reader would presume him to imply it.]
To find the ratio for the sum of two intervals their ratios are multiplied; the ratio for the difference between two intervals is found by dividing their ratios. In Pythagorean intonation the whole tone normally has the ratio 9:8 (obtained by dividing the ratio of the 5th by that of the 4th), and so the major 3rd has the ratio 81:64 (obtained by squaring 9:8). But a pure major 3rd has the ratio 5:4, which is the same as 80:64 and thus smaller than 81:64. (The discrepancy between the two (81:80) is called the syntonic comma and amounts to about one ninth of a whole tone.) Since 5:4 divided by 9:8 equals 40:36, or rather 10:9 (a comma less than 9:8), just intonation has two different sizes of whole tone a feature that tends to go against the grain of musical common sense and gives rise to various practical as well as theoretical complications. Some 18th-century advocates of just intonation and others since have admitted ratios with multiples of 7 (such as 7:5 for the diminished 5th in a dominant 7th chord; see Septimal system). [Monzo: note that the septimal ratios are described as additions to what Lindley leads us to understand as "regular" "just intonation".]
Two medieval British theorists, Theinred of Dover and Walter Odington, suggested that the proper ratio for a major 3rd might be 5:4 rather than 81:64, and some 15th-century manuscript treatises on clavichord making include quintal and, in one instance, septimal ratios (see Lindley, 1980). Quintal ratios were introduced into the mainstream of Renaissance musical thought by Ramis de Pareia, whose famous theoretical monochord (1482) provided just intonation for the notes of traditional plainchant, but with GD, BG and DB implicitly left a comma impure (fig.1a). Thence Ramis derived the 12-note scale by adding two 5ths on the flat side (A and E) and two on the sharp (F and C); in this scheme (fig.1b), CA would make a good 5th, hardly 2 cents smaller than pure. Ramis did not intend or expect this tuning to be used in any musical performances, however, for in his last chapter (giving advice to cantors and describing what he called instrumenta perfecta) he said that GD was a good 5th but CA must be avoided (see Temperaments, 2).
Gioseffo Zarlino (1558) argued that although voices accompanied by artificial instruments would match their tempered intonation, good singers when unaccompanied would adhere to the pure intervals of the diatonic syntonic tetrachord which he had selected (following the example of Ramis's disciple, Giovanni Spataro) from Ptolemy's various models of the tetrachord (fig.2a). Zarlino eventually became aware that this would entail a sour 5th in any diatonic scale consisting of seven rigidly fixed pitch classes (see fig.2b, where DA is labelled dissonant); but he held that the singers' capacity to intone in a flexible manner would enable them to avoid such problems without recourse to a tempered scale and that they must do so because otherwise the natural intervals (those with simple ratios) would never be put into action, and sonorous number would be altogether vain and superfluous in Nature. This metaphysically inspired nonsense was to prove a stimulating irritant in the early development of experimental physics, and during the next three centuries a number of distinguished scientists paid a remarkable amount of attention to the conundrum of just intonation (as well as to various attempts to explain the nature of consonance by something more real than sonorous numbers).
In the 1650s Giovanni Battista Benedetti, a mathematician and physicist, pointed out in two letters to the distinguished composer Cipriano de Rore (who had been Zarlino's predecessor as maestro di cappella at S Marco, Venice) that if progressions such as that shown in ex.1 were sung repeatedly in just intonation, the pitch level would change quite appreciably, going up or down a comma each time. In 1581 Vincenzo Galilei, a former pupil of Zarlino, denied that just intonation was used in vocal music, and asserted that the singers' major 3rd is contained in an irrational proportion rather close to 5:4 and that their whole tones made two equal parts of the said 3rd. In the ensuing quarrels, Vincenzo Galilei's search for evidence against Zarlino's mystical doctrine of the senario (the doctrine that the numbers 1 to 6 are the essence of music) led him to discover by experiment that for any interval the ratio of thicknesses between two strings of equal length is the square root of the ratio of lengths between two strings of equal thickness. This undermined the theoretical status of the traditional ratios of just intonation as far as the eminent Dutch scientist Simon Stevin was concerned; it might have had further consequences had not Galilei retracted in 1589 his 1581 account of vocal intonation, and had not his son Galileo's generation devised the pulse theory of consonance, according to which the eardrum is struck simultaneously by the wave pulses of the notes in any consonant interval or chord (thus mistakenly assuming that the waves are always in phase with one another). Such a theory tended rather to undermine the concept of tempered consonances, where the wave frequencies are theoretically incommensurate.
Descartes found Stevin's dismissal of simple ratios so absurd that I hardly know any more how to reply, but Marin Mersenne advanced the real argument that the superiority of justly intoned intervals is shown by the fact that they do not beat (1636-7). (He probably gained this argument from Isaac Beeckman, who seems to have invented the pulse theory of consonance.) 50 years later, however, Wolfgang Caspar Printz wrote that a 5th tempered by 1/4-comma remains concordant because Nature transforms the confusion into a pleasant beating [which] should be taken not as a defect but rather as a perfection and gracing of the 5th. Andreas Werckmeister agreed (Musicalische Temperatur, 2/1691/R).
About this time Christiaan Huygens developed Benedetti's point (although he did not associate it with Benedetti) in his assertion that if one sings the notes shown in ex.2 slowly, the pitch will fall (just as in ex.1); but if one sings quickly, I find that the memory of the first C keeps the voice on pitch, and thus makes it state the consonant intervals a little falsely. Rameau stated (Generation harmonique, 1737) that an accompanied singer is guided by the temperament of the instruments only for the fundamental sounds (the roots of the triads), and automatically modifies, in the course of singing the less fundamental notes, everything contrary to the just rapport of the fundamental sounds. While this represents a musicianly departure from the common error that there is something natural about the scheme shown in fig.2b, it does rather overlook the fact that the tuning of the fundamental sounds was normally tempered on keyboard instruments and lutes.
The most eminent scientist among 18th-century music theorists, Leonhard Euler, developed an elaborate and remarkably broad mathematical theory of tonal structure (scales, modulations, chord progressions and gradations of consonance and dissonance) based exclusively upon just-intonation ratios. He failed to observe that a 5th tuned a comma smaller than pure sounds sour, and so allowed himself to be misled by an inept passage in Johann Mattheson's Grosse General-Bass-Schule (1731) into supposing that keyboard instruments of his day were actually tuned in just intonation. Euler at first rejected septimal intervals, saying in 1739 that they sound too harsh and disturb the harmony, but declared in 1760 that if they were introduced, music would be carried to a higher degree (an idea previously voiced by Mersenne and Christiaan Huygens). He published two articles in 1764 to demonstrate that music has now learnt to count to seven (Leibnitz had said that music could only count to five).
Another extreme of theoretical elaboration was reached in the early 19th century by John Farey, a geologist, who reckoned intervals by a combination of three mutually incommensurate units of measurement derived from just-intonation ratios. Farey's largest unit was the schisma, which was the difference between the syntonic and Pythagorean commas. (The Pythagorean comma is the amount by which six Pythagorean whole tones exceed an octave; the schisma is some 1.95 cents and has the ratio 32805:32768.) His smallest unit was the amount by which the syntonic comma theoretically exceeds 11 schismas (or by which 11 octaves theoretically exceed the sum of 42 Pythagorean whole tones and 12 pure major 3rds; this is some 1/65-cent, and its ratio would require 49 digits to write out). His intermediate unit (some 0.03 cent) was the amount by which each of the three most common types of just-intonation semitone (16:15, 25:24 and 135:128) theoretically exceeds some combination of the other two units (fig.3) or the amount by which 21 octaves theoretically exceed the difference between 37 5ths and two major 3rds.
2. Instruments.
Rameau reported (1737) that some masters of the violin and basse de viol tempered their open-string intervals an idea also found in the writings of Werckmeister (1691) and Quantz (Versuch einer Anweisung die Flte traversiere zu spielen, 1752). But Boyden has shown (1951) that evidence from the writings of 18th-century violinists, particularly Geminiani and Tartini, points to a kind of just intonation flexibly applied to successive intervals with adjustments when necessary both melodically and harmonically on each of the four strings, tuned in pure 5ths, as points of reference. In the 1760s Michele Stratico, a former pupil of Tartini, worked out a fairly efficient system of notation for this kind of just intonation, including septimal intervals (ex.3).
To model a fretted instrument upon just intonation entails the use of zig-zag frets. Dirck Rembrandtsoon van Nierop, a mathematician who favoured just intonation for all sorts of instruments as well as voices, worked out (1659) an exact fretting scheme for a cittern (fig.4a), according to which, if the open-string intervals were tuned as in fig.4b, then each position on the highest course could be supplied with one or more justly intoned chords as shown in ex.4. Some other devotees of just intonation who designed fretted instruments were Giovanni Battista Doni, Thomas Salmon and Thomas Perronet Thompson (fig.5).
The simplest way to provide all possible pure concords among the naturals of a keyboard instrument with fixed intonation is to have two Ds, one pure with F and A and the other, a comma higher, pure with G and B (fig.6a). (The concept of a diatonic scale in just intonation with two Ds a comma apart goes back to Lodovico Fogliano's Musica theorica, 1529.) If this group of eight notes is then provided with a complement of ten chromatic notes as indicated in fig.6b, each natural will have available all six of its possible triadic concords. This scheme was described by Mersenne and employed by Joan Albert Ban for a harpsichord built in Haarlem in 1639 (for illustration see Ban, joan albert). Mersenne stated that on a keyboard instrument of this type the perfection of the harmony would abundantly repay the difficulty of playing, which organists will be able to surmount in the space of one week.
The justly intoned harmonium of Helmholtz (in mathematical terms not exactly embodying just intonation, but deviating from it insignificantly from a practical and acoustical point of view) combined two normal keyboards for the scheme shown in fig.7 [sorry -- diagram not reproduced; Helmholtz's harmonium was in skhismic temperament. Also see remarks about Helmholtz's tuning on my webpage about Groven's tuning. -Monzo]. The 12 pitch classes shown to the left are on the upper manual, the 12 to the right on the lower manual. No justly intoned triadic note is present beyond the lines along the top and bottom of the diagram, but the three notes at the right end (A, C or D, and E) make justly intoned triads with the three at the left (E, G or A, and C). Thus the major and minor triads on F, A, and D or C require the use of both manuals at once. The 12 pitch classes shown in the upper half of the diagram are each a comma lower in intonation than their equivalents in the lower half of the diagram. Every 5th except CG or DA is available at two different pitch levels a comma apart, and the same is true of six triads: the major ones on E, B and F, and the minor ones on G, D or E, and B. In the case of triads on C, D, F, G and A, however, the major triad is always intoned a comma higher than its parallel minor triad.
Various other elaborate keyboard instruments capable of playing in just or virtually just intonation have been built by Galeazzo Sabbatini, Doni, H.W. Poole, H. Liston, R.H.M. Bosanquet, S. Tanaka, Eitz, Partch, the Motorola Scalatron Corporation and others (see Microtonal instruments). Playing such an instrument involves choosing which form of each note to use at which moment. If the proper choice is consistently made, impure vertical intervals will be avoided and the occurrence of impure melodic ones minimized. The criteria for choosing, which differ in detail with each kind of elaborate keyboard pattern, are intricate but capable of being incorporated in a pattern of electric circuits amounting to a simple computer programme. In 1936 Eivind Groven, a Norwegian composer and musicologist, built a harmonium with 36 pitches per octave tuned to form an extension of Helmholtz's quasi-just-intonation scheme, but with a normal keyboard, the choice of pitch inflections being made automatically while the performer plays as on a conventional instrument. He later (1954) devised a single-stop pipe organ of the same type, now at the Fagerborg Kirke in Oslo, a complete electronic organ with 43 pitches per octave (1965), now at the Valerencen Kirke in Oslo, and a complete pipe organ incorporating his invention (c1970, built by Walcker & Cie.). Groven's work has made just intonation practicable on keyboard instruments that are no more difficult to play than ordinary ones.
While the distinctive quality of justly intoned intervals is unmistakable, their aesthetic value is bound to depend upon the stylistic context. In 1955 Kok reported, on the basis of experiments with an electronic organ capable of performing in various tuning systems, that musicians, unlike other listeners, heard the difference between equal and mean-tone temperaments, giving preference to the latter, and a fortiori the just intonation, but only in broad terminating chords and for choral-like music. However, they do not like the pitch fluctuations caused by instantaneously corrected thirds. According to McClure (Studies in Keyboard Temperaments, GSJ, i, 1948, pp.2840), George Bernard Shaw recalled that in the 1870s the progressions of pure concords on Bosanquet's harmonium (with 53 pitches in each octave) had sounded to him unpleasantly slimy. E.H. Pierce (1924), describing the 1906 model of the Telharmonium, which was capable of being played in just intonation with 36 pitches in each octave, reported:
The younger players whom I taught at first followed out my instructions, but as time went on they began to realize (as in fact I did myself) that there is a spirit in modern music which not only does not demand just intonation, but actually would suffer from its use, consequently they relapsed more and more into the modern tempered scale. The composer and theorist J.D. Heinichen remarked (Der General-Bass in der Composition, 1728, p.85) that because keys with two or three sharps or flats in their signature were so beautiful and expressive in well-tempered tunings, especially in the theatrical style, he would not favour the invention of the long-sought pure-diatonic keyboard even if it were to become practicable. These remarks suggest that the recently achieved technological feasibility of just intonation on keyboard instruments is but a step towards its musical emancipation and that further steps are likely to depend on the resourcefulness of composers who may be inclined in the future to discover and exploit its virtues.
BIBLIOGRAPHY
to 1800
B. Ramis de Pareia: Musica practica (Bologna, 1482, 2/1482/R; Eng. trans., 1993)
G. Spataro: Errori de Franchino Gafurio da Lodi (Bologna, 1521)
G. Zarlino: Le istitutioni harmoniche (Venice, 1558/R, 3/1573/R; Eng. trans. of pt iii, 1968/R, as The Art of Counterpoint; Eng. trans. of pt iv, 1983, as On the Modes)
G. Zarlino: Dimostrationi harmoniche (Venice, 1571/R) F. de Salinas: De musica libri septem (Salamanca, 1577, 2/1592; Sp. trans., 1983)
V. Galilei: Dialogo della musica antica et della moderna (Florence, 1581/R; partial Eng. trans. in StrunkSR1)
G.B. Benedetti: Diversarum speculationum mathematicarum & physicarum liber (Turin, 1585), 282
G. Zarlino: Sopplimenti musicali (Venice, 1588/R)
V. Galilei: Discorso intorno all'opere di Messer Gioseffo Zarlino da Chioggia (Florence, 1589/R)
S. Stevin: Vande spiegheling der singconst, c1600, ed. D. Bierens de Haan (Amsterdam, 1884); ed. A. Fokker in The Principal Works of Simon Stevin, v (Amsterdam, 1966), 41364 [incl. Eng. trans.]
G.M. Artusi: Considerationi musicali, appx to Seconda parte dell'Artusi (Venice, 1603/R)
Mersenne, Marin: Traité de l'harmonie universelle, contenant la théorie et la pratique de la musique. (Paris, 1627); English translation Harmonie Universelle: The Books on Instruments by Roger Edington Chapman, (The Hague, 1957).
G.B. Doni: Compendio del trattato de' generi e de' modi della musica (Rome, 1635)
M. Mersenne: Harmonicorum libri, in quibus agitur de sonorum natura (Paris, 1635-36)
G.B. Doni: Annotazioni sopra il Compendio de' generi e de' modi della musica (Rome, 1640)
D.R. van Nierop: Wis-konstige musyka (Amsterdam, 1659)
I. Newton: unpubd MSS on music, 1665 (GB-Cu Add.4000)
C. Huygens: writings on music, ed. in Oeuvres compltes, xx (The Hague, 1940)
W.C. Printz: Exercitationes musicae theoretico-practicae curiosae, iiiv (Dresden, 16878)
T. Salmon: A Proposal to Perform Musick in Perfect and Mathematical Proportions (London, 1688)
T. Salmon: The Theory of Musick Reduced to Arithmetical and Geometrical Proportion, Philosophical Transactions of the Royal Society, xxiv (1705), 207277
J. Mattheson: Grosse General-Bass-Schule, oder, Der exemplarischen Organisten-Probe zweite, verbesserte und vermehrte Auflage (Hamburg, 1731/R)
P. Prelleur: The Modern Musick-Master, or The Universal Musician, v: The Art of Playing on the Violin (London, 1731/R)
L. Euler: Tentamen novae theoriae musicae (St Petersburg, 1739) repr. in Opera omnia, III/i (Leipzig, 1926), 197427; Eng. trans. in C.S. Smith: Leonhard Euler's Tentamen novae theoriae musicae (diss., Indiana U., 1960)
F. Geminiani: The Art of Playing the Violin (London, 1751/R1952 with introduction by D.D. Boyden)
G. Tartini: Trattato di musica secondo la vera scienza dell'armonia (Padua, 1754/R; Eng. trans. in F.B. Johnson: Tartini's Trattato di musica secondo la vera scienza dell'armonia (diss., Indiana U., 1985)
G.B. Doni: Lyra Barberina amphicordos, ed A.F. Gori and G.B. Passeri (Florence, 1763/R)
L. Euler: Conjecture sur la raison de quelques dissonances gnralement reues dans la musique; Du vritable caractre de la musique moderne, Mmoires de l'Academie royale des sciences et des belles lettres de Berlin, xx (1764), 165, 17499; repr. in Opera omnia, iii/1, 50815, 51639
L. Euler: Lettres une princesse d'Allemagne (Berne, 1775, many later edns; Eng. trans., 1975)
M. Stratico: MS treatises on music (I-Vsm it. iv 3413)
since 1800
H. Liston: An Essay on Perfect Intonation (Edinburgh, 1812)
J. Farey: On Different Modes of Expressing the Magnitudes and Relations of Musical Intervals, American Journal of Science, ii (1820), 74
T.P. Thompson: Instructions to my Daughter for Playing on the Enharmonic Guitar (London, 1829)
H.W. Poole: An Essay on Perfect Intonation in the Organ, American Journal of Science and the Arts, 2nd ser., ix (1850), 6883, 199216
M. Hauptmann: Die Natur der Harmonik und der Metrik (Leipzig, 1853, 2/1873; Eng trans., 1888/R)
C.E.L. Delezenne: Table de logarithmes acoustiques (Lille, 1857)
T.P. Thompson: On the Principles and Practice of Just Intonation with a View to the Abolition of Temperament (London, 1860)
H. von Helmholtz: Die Lehre von den Tonempfindungnen als physiologische Grundlage fr die Theorie der Musik (Brunswick, 1863, 6/1913/R; Eng. trans., 1875, as On the Sensations of Tone, 2/1885/R)
G. Engel: Das mathematische Harmonium (Berlin, 1881)
S. Tanaka: Studier im Gebiete der reinen Stimmung, VMw, vi (1890), 190
C.A. Eitz: Das mathematisch-reine Tonsystem (Leipzig, 1891)
M. Planck: Die naturliche Stimmung in der modernen Vokalmusik, VMw, ix (1893) 41840
E.P.L. Atkins: Ear-Training and the Standardization of Equal Temperament, PMA, xli (191415), 91111
E.H. Pierce: A Colossal Experiment in Just Intonation, MQ, x (1924), 32632
N.L. Norton: A New Theory of Untempered Music, MQ, xxii (1936), 21733
J.M. Barbour: Just Intonation Confuted, ML, xix (1938), 4860
E. Groven: Temperering og renstemning [Temperament and tuning] (Oslo, 1948; Eng. trans., 1970)
J.M. Barbour: Tuning and Temperament: a Historical Survey (East Lansing, MI, 1951/R, 2/1953)
D. Boyden: Prelleur, Geminiani, and Just Intonation, JAMS, iv (1951), 20219
E. Groven: My Untempered Organ, Organ Institute Quarterly, v/3 (1955), 34
W. Kok: Harmonische orgels (The Hague, 1955) [with Eng. summary]
H. Stephani: Zur Psychologie des musikalischen Hrens: Hren wir naturrein, quintengestimmt, temperiert? (Regensburg, 1956)
C.V. Palisca, ed.: Girolamo Mei (15191594): Letters on Ancient and Modern Music to Vincenzo Galilei and Giovanni Bardi, MSD, iii (1960, 2/1977)
C.V. Palisca: Scientific Empiricism in Musical Thought, Seventeenth Century Science and the Arts, ed. H. Rhys (Princeton, 1961), 91137; repr. in C. Palisca: Studies in the History of Italian Music and Music Theory (New York, 1994), 20035
Ll.S. Lloyd: Intervals, Scales and Temperaments, ed. H. Boyle (London, 1963, 2/1978)
C. Dahlhaus: Die Reine Stimmung als musikalisches Problem, Festskrift til Olav Gurvin, ed. F. Benestad and P. Krmer (Drammen and Oslo, 1968), 4955 R. Dammann: Die Musica mathematica von Bartolus, AMw, xxvi (1969), 14062 E. Groven: Equal Temperament and Pure Tuning (Oslo, 1969)
D.P. Walker: Studies in Musical Science in the Late Renaissance (London, 1978)
M. Lindley: Pythgorean Intonation and the Rise of the Triad, RMARC, no.16 (1980) 461
M. Lindley: Der Tartini-Schuler Michele Stratico, GfMKB: Bayreuth 1981, 36670
M. Lindley: Leonhard Euler als Musiktheoretiker, GfMKB: Bayreuth 1981, 54753
R. Rasch: Ban's Intonation, TVNM, xxxiii (1983), 7599
M. Lindley: Lutes, Viols and Temperaments (Cambridge, 1984)
M. Lindley: Stimmung und Temperatur, Hren, Messen und Rechnen in der frhen Neuzeit, ed. F. Zaminer (Darmstadt, 1987), 109331
For further bibliography see Temperaments.
See also the huge online Tuning and Temperaments Bibliography.
Updated:
2003.02.09 -- added interval-matrix
2002.3.15
2002.1.26