Definitions of tuning terms
© 1998 by Joseph L. Monzo
All definitions by Joe Monzo unless otherwise cited
meantone
a system of tuning in which the two JI
"whole tones"
(with ratios of 9:8 and 10:9)
are conflated into one "mean tone" which lies between
the two, the objective being to produce or approximate
JI "major 3rd"s
(with a ratio of 5:4) but to eliminate
the syntonic comma and its associated
problem of commatic drift by
having only one size of whole-tone.
The "5th"
is flatter (by a fraction of a syntonic
comma) than the just 3:2, and this is normally how the tuning is
described. Thus the names
"Quarter-comma meantone",
"2/9-comma meantone", etc.
The elimination of the syntonic comma means that the
essential feature of meantone and meantone-like systems
is the equation of the
"major 3rd"
with four "5ths".
[Note that while ETs
create a closed system, most meantones do not.]
While the whole point of meantones, as explained above,
is to collapse the 2-dimensional
"8ve"-equivalent
5-limit
lattice into a
1-dimensional linear temperament
which emulates (in notation, but not in tuning) the linear
Pythagorean system,
it so happens that certain meantones can provide very good
approximations to higher odd/prime limits.
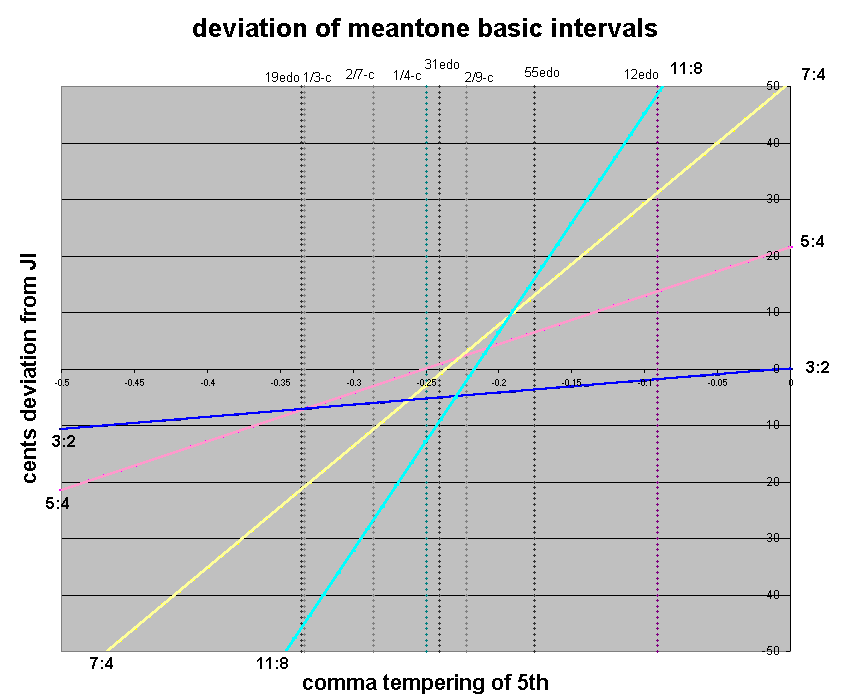
Below is a graph showing the deviation of the basic intervals
in meantone from their JI equivalents
in the 11-limit. The horizontal axis
represents the fraction-of-a-comma
amount by which the meantone generator
(i.e., the "5th") is
tempered (narrowed)
from the Pythagorean
"pure 5th" of ratio 3:2.
The vertical axis shows the deviation in
cents
from the JI intervals, of 1 generator from 3:2 (blue line),
4 generators ("8ve"-equivalent)
from 5:4 (pink), 10 generators from 7:4 (yellow),
and 18 generators from 11:8 (cyan). Some common meantones are
drawn vertically as illustrations. (In this graph an alternative
mapping of 11:8, to -13 generators, is not shown. All of these
graphs choose one particular mapping of 11-limit ratios, as shown
at the bottom of the "meantone error" applet which can be viewed
by clicking on the small graph below.)
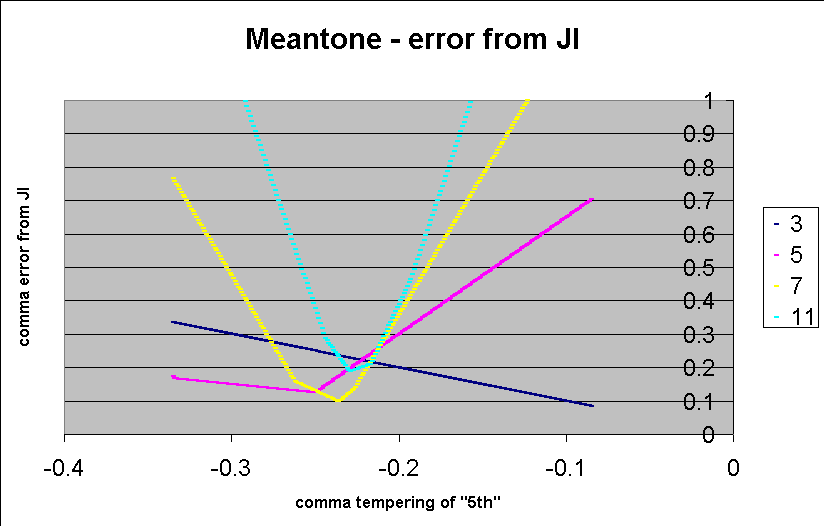
Below is a graph showing the average absolute deviation
for each set of ratios of prime-factors.
Below is a closeup of the central section from the
above graph.
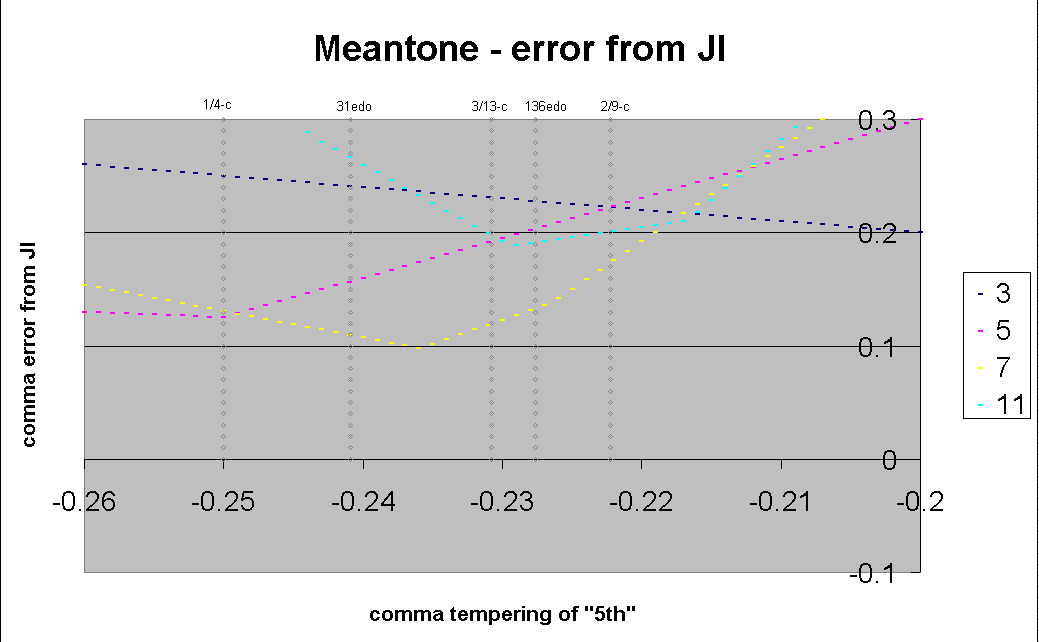
If one follows Partch's observation that the sensitivity of
a ratio to mistuning is directly proportional to its
prime- (or odd-) limit, it can be seen from the above graph
that the area between 0.229- and 0.217-comma meantone is pretty close
to ideal for a meantone representing 11-limit harmony using
the mapping I chose.
|
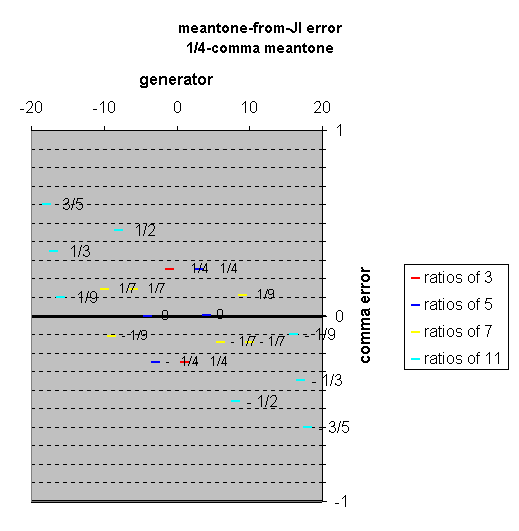
|
Click on the graphic at left to open a new window with a
mouse-over applet which shows the error of various specific
meantones from JI.
|
[from Joe Monzo, JustMusic: A New Harmony]
(see also my paper explaining the derivation of
W. S. B. Woolhouse's optimal meantone, and Graham Breed's excellent
Meantone Temperaments webpage.)
...............................
[from John Chalmers:]
...the definition of
meantone could be tightened up a bit as it implies that all
meantone-like tunings have 5/4 major thirds. I would describe meantone
[that is, meantone proper] as the temperament whose fifth is equal to the fourth root of 5 and is
thus 1/4 of a syntonic comma flatter than 3/2.
Meantone-like temperaments are those cyclic systems which have fifths
flatter than 3/2 by some fraction (rational or
irrational) of the
syntonic comma and which form their major thirds by four ascending
fifths reduced by two octaves. Such tunings divide the ditone (which is
here equivalent to the major third) into two equal "mean tones"
Well-known examples include the 1/3-comma (just 6/5 and 5/3), the
1/5-comma (just 15/8, 16/15), and John Harrison's tuning whose major
third equals 2(1/pi) and which has been revived and promoted in an
extended form by Charles Lucy.
Certain meantone-like temperaments are audibly equivalent to equal
temperaments of the octave. For example, the 1/4-comma system
corresponds to 31-tet and the 1/3 comma to 19-tet. Arbitrarily close
equivalences may be found by using continued fractions or Brun's
Algorithm.
The upper limit of meantone-like fifths is the fifth of 12-tone ET (700
cents) and the upper limit of meantone-like major thirds is the major
third of 12-tet
(400 cents).
(While Pythagorean tuning could be considered
as a meantone-like system
in which the tempering fraction is zero, temperaments whose fifths are
larger than 700 cents are best thought of as positive systems, which
make their major thirds by a chain of 8 descending fifths (or ascending
fourths). These major thirds are formally diminished fourths (e.g.,
C-Fb). Other relations occur as the fifth become still sharper (9 fifths
up, augmented second, C-D#).)
[from John Chalmers, personal communication]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[from Paul Erlich:]
From: Paul H. Erlich
Sent: Monday, December 20, 1999 7:24 PM
To: 'tuning@onelist.com'
Subject: Summary of optimal meantone tunings
Here is a summary of the meantone tunings (giving the size of fifth in
cents, the fraction of the syntonic comma by which the fifth is reduced,
and the first known advocate or reference to a TD posting by me from Brett
Barbaro's e-mail) that are optimal under various error criteria for the
three "classical" consonant interval classes: the one 3-limit interval,
the p4/p5; and the two 5-limit intervals, the m3/M6 and the M3/m6.
| Max. error |Sum-squared error|Sum-absolute error|
---------+------------+-----------------+------------------+
Inverse | 697.3465 | 696.5354 | 696.5784 |
Limit | 3/14-comma | 63/250-comma | 1/4-comma |
Weighted | Riccati |TD 162.10 5/5/99 | Aron |
---------+------------+-----------------+------------------+
Equal | 696.5784 | 696.1648 | 696.5784 |
Weighted | 1/4-comma | 7/26-comma | 1/4-comma |
| Aron | Woolhouse | Aron |
---------+------------+-----------------+------------------+
Limit | 695.9810 | 696.0187 | 696.5784 |
Weighted | 5/18-comma | 175/634-comma | 1/4-comma |
| ~Smith | Erlich (TTTTTT) | Aron |
---------+------------+-----------------+------------------+
m3/M6 & | 695.8103 | 695.9332 | 696.5784 |
M3/m6 | 2/7-comma | 7/25-comma | 1/4-comma |
only | Zarlino | This may be new | Aron |
---------+------------+-----------------+------------------+
================================================================
From: "Paul H. Erlich"
To: "'monz@juno.com'"
Cc: "'tuning@onelist.com'"
Date: Fri, 11 Feb 2000 21:14:05 -0500
Subject: Summary of historical meantone tunings
[subsequently expanded by Erlich & Op de Coul]
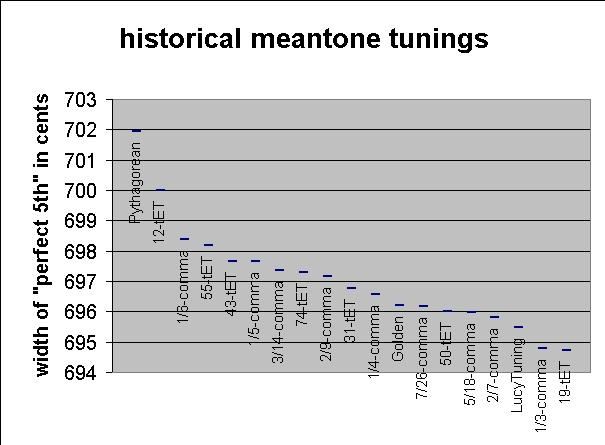
Summary of historical meantone tunings
[ranked by size of '5th']
Variety Theorist Date Minor Third Major Third Fifth
Pythagorean Ling Lun c.2000BC 294.13¢ 407.82¢ 701.96¢
12-tET Tsai-yü 1596 300.00 400.00 700.00
1/6-comma Silbermann <1748 304.89 393.48 698.37
55-tET Beer <1722 305.45 392.73 698.18
43-tET Sauveur 1701 306.98 390.70 697.67
1/5-comma Verheyen c.1600 307.04 390.62 697.65
Sauveur 1701
3/14-comma Riccati 1762 307.96 389.39 697.35
74-tET Riccati 1762 308.11 389.19 697.30
2/9-comma Rossi 1666 308.47 388.70 697.18
Drobisch 1855
31-tET *Vicentino 1555 309.68 387.10 696.77
1/4-comma *Aron 1523 310.26 386.31 696.58
Golden Kornerup 1930 311.36 384.86 696.21
7/26-comma Woolhouse 1835 311.51 384.66 696.16
50-tET Henfling 1710 312.00 384.00 696.00
5/18-comma Smith 1749 312.06 383.92 695.98
2/7-comma Zarlino 1558 312.57 383.24 695.81
LucyTuning Harrison 1775 313.52 381.97 695.49
1/3-comma Salinas 1577 315.64 379.15 694.79
19-tET Costeley 1558 315.79 378.95 694.74
1/2-comma Fogliano 1529 326.39 364.81 691.20
* For some cautionary annotations by Margo Schulter
concerning Aron and Vicentino in this table, see her
Tuning List posting of Sun Feb 13, 2000 11:24pm,
which appeared in Onelist Tuning Digest # 532, message 12.
Note also that while Aron was the first theorist to give
a thorough description of 1/4-comma meantone, Arnold Schlick
was the first to desribe to describe it at all,
in 1511 [Schlick, Arnold. Spiegel der Orgelmacher und Organisten. Speyer, 1511. Monatshefte für Musikgeschichte, Heidelberg, 1869. Reprint 1959. English translation by E.B. Barber, Frits Knuf, Buren, 1980.]. See
this German webpage.
|

|
Click on the image at left
to open a window with animated graphs comparing various meantone
chains.
|
Meantone cycles which are based on
tempering
by a fraction of a syntonic comma, which is a
5-limit
interval,
can have some of their pitches graphed on a
lattice diagram.
(I explained the mathematics of one example of this
-- 1/6-comma meantone equating to a cycle of 64:45's --
in Yahoo Tuning List
message #30125,
Date: Tue Nov 13, 2001 6:55 am,
Subject: Re: New Telemann page - audio files).
Below is a 5-limit lattice illustrating partial
cycles of the most common meantone tunings; the cell
containing the reference pitch "C" is colored black
because all the cycles contain it, and thus all the
axes which represent the different cycles pass
thru and are centered on that point on the lattice.
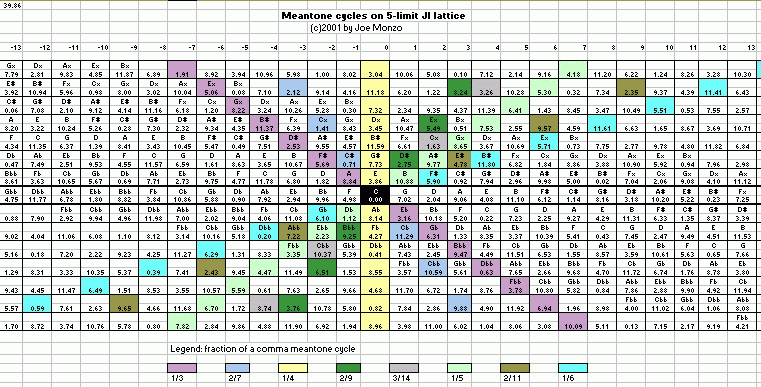
Applet: representation of meantone tunings as JI-interval cycles
©2001 by Joe Monzo
(inspired by this
lattice
applet by Ming Sun Ho)
Below is an applet illustrating several examples of the
cycles on the above diagram.
MouseOver the names of the various fraction-of-a-comma
meantone cycles
to see a graph of the notes on a
5-limit
lattice diagram.
Each blue square on the graph represents a "cell" or
ratio-point
on the lattice, with powers of 3 along the horizontal axis
and powers of 5 along the vertical axis. The plots of these
cells gives each meantone cycle a unique angle and density.
The ratios of generator g in n/d-comma meantone
are plotted as 3x * 5y,
where x = (d-(4*n))*g and y = n*g.
These meantone cycles can be approximated arbitrarily closely
by various
EDO cycles,
for example, 1/3-comma equates to 19-EDO (generators -9 to +9),
1/4-comma to 31-EDO (generators -15 to +15),
1/5-comma to 43-EDO (generators -21 to +21),
1/6-comma to 55-EDO (generators -27 to +27),
1/11-comma to 12-EDO (generators -6 to +5 or -5 to +6),
etc. I have not taken this into account on these graphs, and
simply arbitrarily extend each cycle from -22 to +22 generators.
Meantones as JI-interval chains
©2001 by Joe Monzo
1/2
1/3
2/7
5/18
7/26
1/4
2/9
3/14
1/5
2/11
3/17
1/6
1/11
I expanded on the above idea to create a set of diagrams
which I think are really useful:
Lattice
diagrams comparing rational implications
of various meantone chains.
Below are some crude ASCII lattice diagrams which
accurately portray the nature of meantone intervallic
relationships. These are flat projections of what
are intended to be cylindrical diagrams.
The dotted line represents a circle whereby
pitches wrap around the cylinder to occupy the same point.
Here is the meantone diatonic C-major scale:
,,-F
,,-C-'' / \
,,-G-'' / \ / \
..D-''../.\.../...\./..,,-D..
\ / \ / ,,-A-''
\ / ,,-E-''
B-''
Here is a typical 12-tone meantone system:
,,-Eb
,,-Bb'' / \
..F-''.../.\.../...\....,,-F..
\ / \ / ,,-C-'' / \
\ / ,,-G-'' / \ / \
..D-''../.\.../...\./..,,-D..
\ / \ / ,,-A-'' / \
\ / ,,-E-'' / \ / \
..B-''../.\.../...\./...,,-B..
\ / \ / ,,-F#-''
\ / ,,-C#-''
..G#-''
And meantones were also used with pitch-sets
larger than 12 notes, thus:
,,-Fb
..Cb''.../.\...........,,-Cb..
\ / \ ,,-Gb'' / \
\ / ,,-Db'' / \ / \
..Ab''.../.\.../...\./..,,-Ab..
\ / \ / ,,-Eb'' / \
\ / ,,-Bb'' / \ / \
..F-''.../.\.../...\./..,,-F..
\ / \ / ,,-C-'' / \
\ / ,,-G-'' / \ / \
..D-''../.\.../...\./..,,-D..
\ / \ / ,,-A-'' / \
\ / ,,-E-'' / \ / \
..B-''../.\.../...\./...,,-B..
\ / \ / ,,-F#-'' / \
\ / ,,-C#-'' / \ / \
..G#-''./.\.../...\./..,,-G#..
\ / \ / ,,-D#'' / \
\ / ,,-A#-'' / \ / \
..E#''../.\.../...\./..,,-E#..
\ / \ / ,,-B#'' / \
\ / ,,-Fx'' / \ / \
..Cx''../.\.../...\./..,,-Cx..
\ / \ / ,,-Gx''
\ / ,,-Dx''
..Ax''
The proper way to lattice a meantone, or any
linear temperament,
is as a cylinder which runs perpendicular to the
vector of the interval being tempered out.
Here is a Monzo lattice of 1/4-comma meantone,
with a typcial 12-tone Eb...G# scale showing along
the meantone chain on the face of the cylinder.
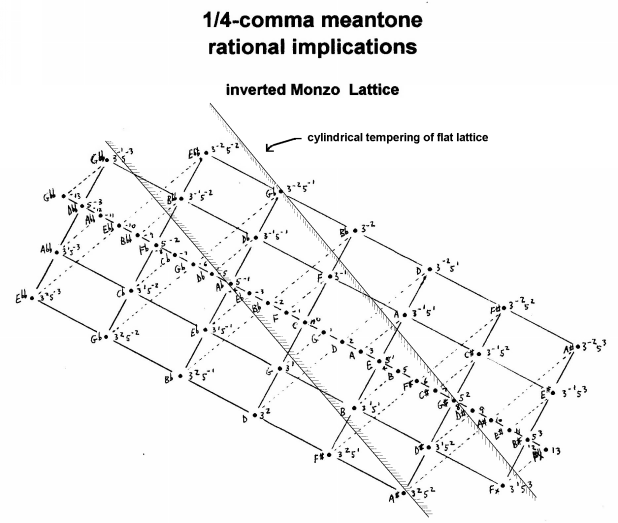
The cylinder for all meantones will always have the
same angle to the lines on my JI lattice, because they
all temper out the same interval, the
syntonic comma. On my lattices,
each meantone chain itself will spiral around the cylinder
differently depending on the fraction of a comma by which
the "5th" is tempered.
Comparison of 19edo and 31edo
Two of the earliest, commonest, and most convenient forms
of meantone tuning are 19edo
and 31edo. Below is a table
and graph comparing their "cycle of 5ths".
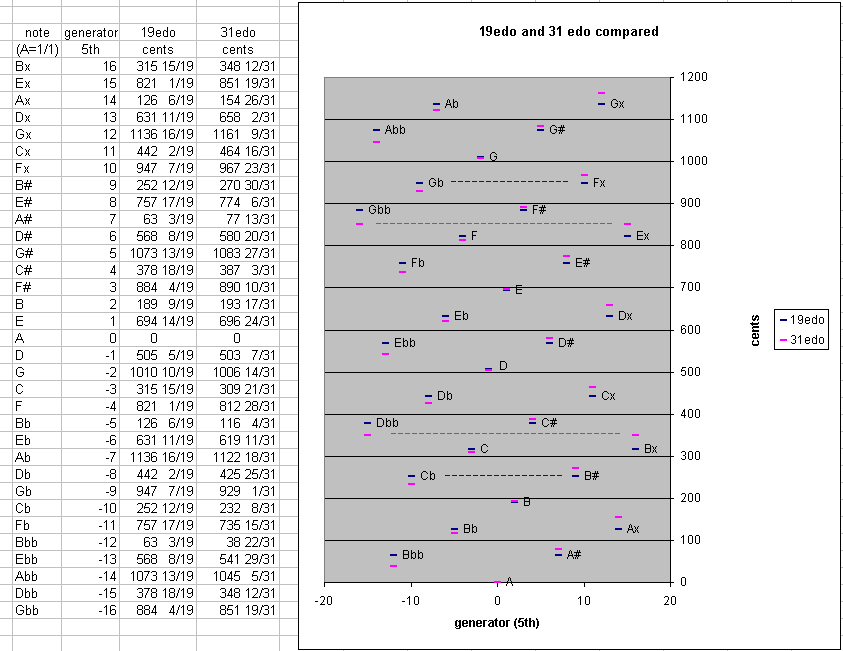
Updated:
2003.08.01 -- added final section comparing 19edo and 31edo chains
2003.03.13 -- added graphs and text showing absolute average error from JI
2003.03.03 -- added "meantone deviation" graph
2003.02.28 -- corrected date of 2/7-comma description to 1558
2003.02.26 -- added the "chronology of meantone advocacy" graph
2002.09.22 -- added the bit about how 4 "5ths" = "major 3rd"
2002.01.27
2001.12.9
2001.11.13
|
(to download a zip file of the entire Dictionary,
click here)
|
For many more diagrams and explanations of historical tunings, see
my book.
If you don't understand my theory or the terms I've used,
start here
|









