It is known that Leopold Mozart taught his son Wolfgang to use a meantone tuning where "flats" would be higher in pitch than "sharps". There is no documentation as to exactly what this tuning was, but there are a few clues.
Paul Erlich quoted in Yahoo Tuning List message 24125 (Thu May 31, 2001 9:03 pm) from Chesnut 1977 as follows:
Leopold Mozart refers to Tosi in general terms as an authoritative source in a letter to Wolfgang from Salzburg dated June 11, 1778. Tosi, in 1723, considered the correct tuning system to be what we would today call a form of regular meantone temperament ... according to Tosi, the large diatonic half step is theoretically equal to five ninths of a whole step, and the small chromatic half step is theoretically four-ninths of a whole step. Tosi thereby divides the octave into fifty-five equal parts. This is equivalent to tempering the perfect fifth by approximately one-sixth of a 'comma,' ...Leopold Mozart, in his violin method of 1756 -- which happens to be the year of Wolfgang's birth -- also describes what we have called 'extended regular meantone temperament' as the correct intonation for the violin; he tells us that keyboard instruments of his time were played with some form of tempered [i.e., well-tempered] tuning, but that in the "right ratio" [i.e., meantone] tuning that he recommends for the violin, flats are higher by a comma than enharmonically equivalent sharps. It can be shown that for whichever of the standard commas we choose, the perfect fifths in Leopold Mozart's system were theoretically flattened by about one-sixth of that comma . . . Leopold Mozart wrote down a couple of scales specifically intended for practice in intonation, one leading through the flats, the other through the sharps. In practicing these scales, the student is supposed to learn to distinguish between the large diatonic half steps and the small chromatic half steps. It is important to emphasize that these scales are not abstractions but exercises to be mastered . . .
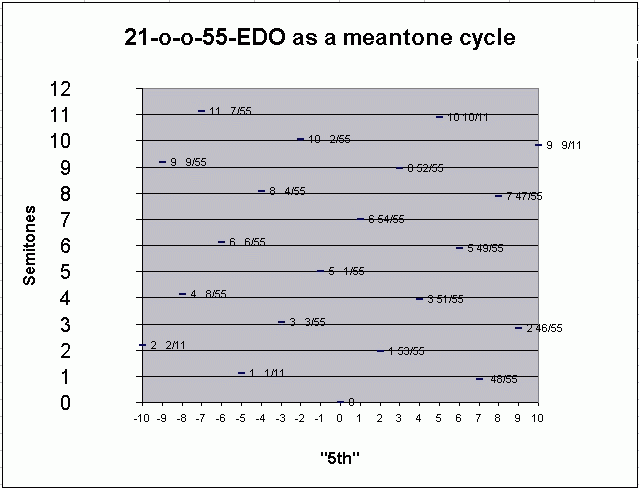
Thus it is apparent that for instruments other than keyboards (which both Mozart and his predecessors tuned in various well-temperaments, typically resembling 1/6-comma meantone for the "natural" notes, and Pythagorean for the "chromatic" keys), Mozart's tuning would be based on 55-EDO, or something very closely approximating it. It would have the following sizes for the basic intervals:
ratio Semitones cents
1 55-EDO degree 2(1/55) 12/55 21 9/11
smaller (chromatic) semitone 2(4/55) 48/55 87 3/11
larger (diatonic) semitone 2(5/55) 1 1/11 109 1/11
whole tone 2(9/55) 1 53/55 196 4/11
55-EDO renders two different-sized semitones but only one size whole-tone; thus, it is a meantone. (Compare with the 50-EDO tuning recommended as a very close approximation to an "optimal meantone" by Woolhouse in 1835; and contrast with 53-EDO, which is so close to both Pythagorean and 5-limit JI that it gives two different-sized whole-tones.)
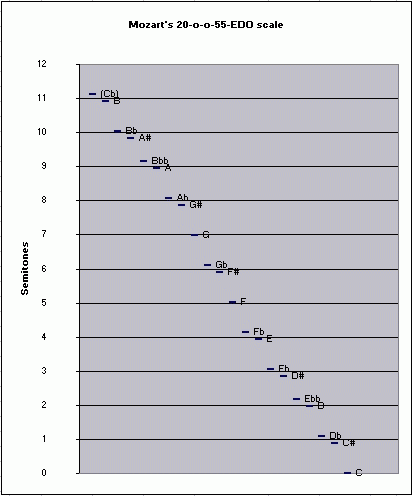
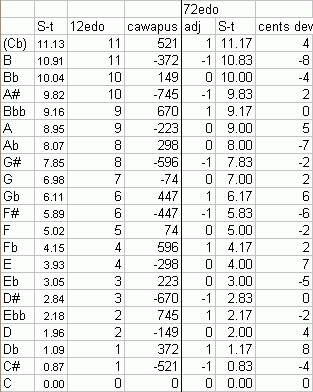
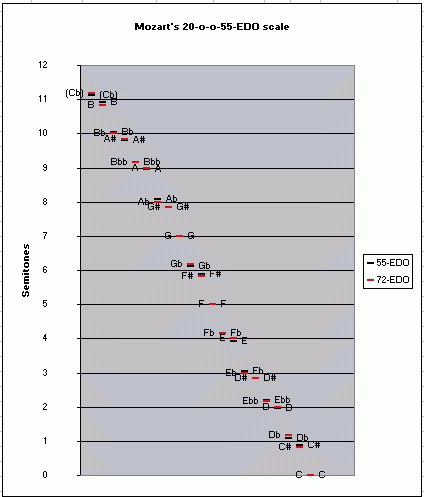
On this webpage I will first explore a 12-tone subset of 55-EDO, as I had mistakenly thought that it was the most likely intended tuning for Mozart's music. I have since learned that Mozart actually intended an interesting 20-tone subset of 55-EDO, and I give an update below on that. I decided to keep the info about the 12-tone subset because many people with ordinary Halberstadt keyboards may wish to explore that subset of 55-EDO, as it still gives a nice meantone system.
Note that for non-keyboard instruments, Mozart's actual conception of this tuning extended in a meantone cycle from Ebb to A#, with Cb omitted, for a total of 20 notes, thus giving two different pitches for the pairs of "sharp and "flat" notes (which are each one "black key" on the Halberstadt keyboard), and alternates for several of the "natural" notes too. So there is no evidence that Mozart ever actually used or advocated a 12-tone subset of this tuning (which is what I present here).
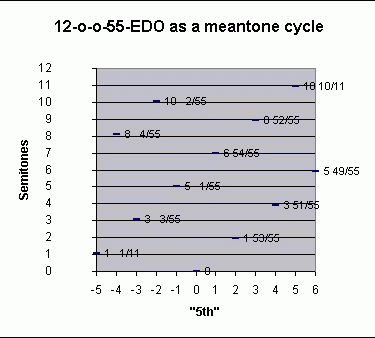
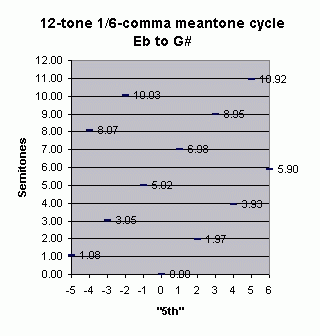
The mapping uses "D" as the symmetrical pitch center, and renders the 12-tone subset as a meantone "cycle of 5ths" from Eb to G#, with the "wolf" appearing between those two pitches.
Note that 55-EDO is audibly identical to 1/6-comma meantone. The "5th" in 55-EDO,
2(32/55) = ~698.181818... cents,is equivalent to that of ~0.175445544-comma meantone. To describe that in terms of low-integer fraction-of-a-comma meantones, that's
- a little less than 1/5 (just slightly more than 3/16, extremely close to 7/37, and almost exactly 10/53) of a cent narrower than the 1/6-comma meantone "5th" = ~698.3706193 cents,
- even closer (less than 1/7 of a cent wider) to the 2/11-comma meantone "5th" = ~698.0447664 cents,
- much closer (~1/46-cent wider) to the 3/17-comma meantone "5th" = ~698.1597733 cents,
- closer still (less than 1/100-cent narrower) to the 7/40-comma meantone "5th" = ~698.1914002 cents,
- and almost bang on (~1/6692-cent wider) the 10/57-comma meantone "5th" = ~698.1819676 cents.
The amount of tempering in 1/6-comma meantone is:
(81/80)(1/6) = (2-4 * 34 * 5-1)(1/6) = 2(-2/3) * 3(2/3) * 5(-1/6)
= ~3.584381599 cents = ~3 & 3/5 cents.
So the 1/6-comma meantone "5th" is (3/2) / ((81/80)(1/6)). Using vector addition, that's:
2^ 3^ 5^
| -1 1 0 | = 3/2
- | -2/3 2/3 -1/6 | = (81/80)(1/6)
-----------------------
| -1/3 1/3 1/6 | = 1/6-comma meantone "5th"
= ~698.3706193 cents.
Using vector addition again to compare the 1/6-comma meantone "5th" with the 55-EDO "5th", we get:
2^ 3^ 5^
| -1/3 1/3 1/6 | = 1/6-comma meantone "5th"
- | 32/55 0 0 | = 55-EDO "5th"
-------------------------
| -151/165 1/3 1/6 | = 1/6-comma "5th" "-" 55-EDO "5th"
= ~0.188801084 cent = ~1/5 or ~10/53 cent, as stated above.
Below I present a side-by-side comparison of 55-EDO and 1/6-comma meantone.
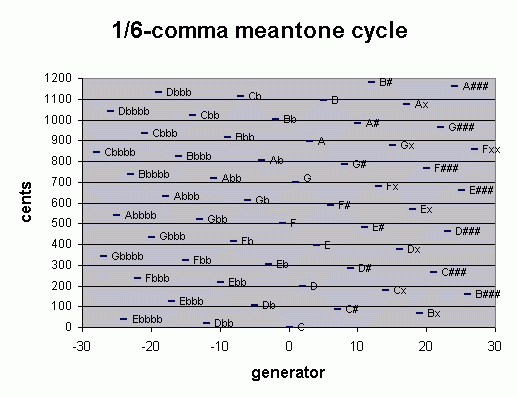
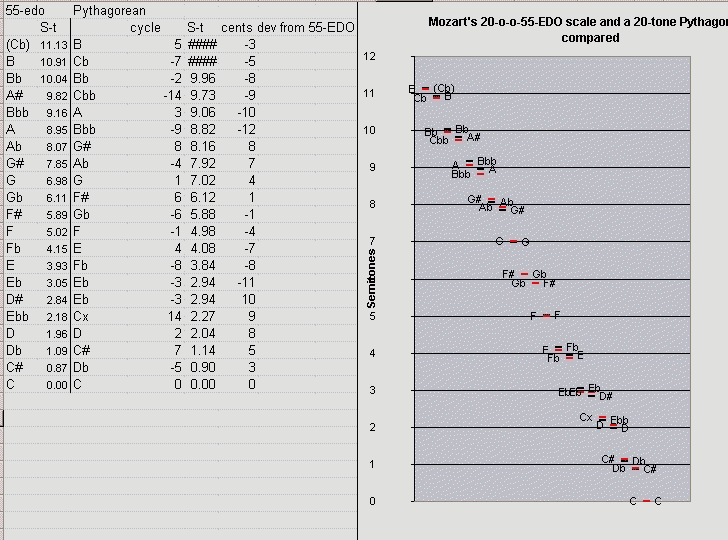
First, the 12-out-of-55-EDO subset and the 12-tone 1/6-comma meantone presented as cycles of "5ths" from Eb to G#:
|
|
|
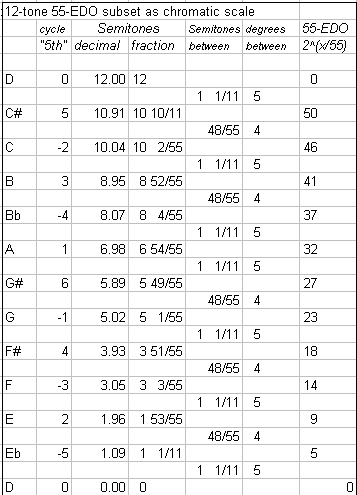
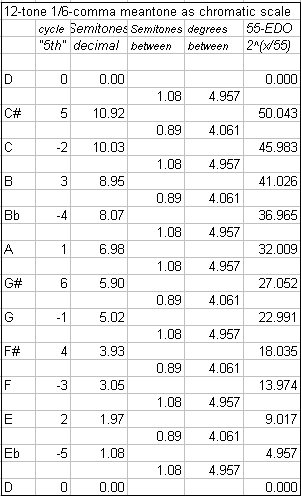
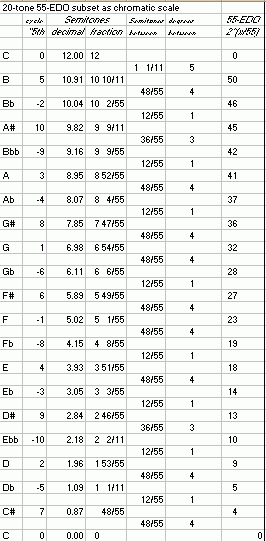
Next, both of the scales presented as 12-tone chromatic scales, with their cycle-of-"5ths" and Semitone values, the Semitones and 55-EDO degrees between notes in the scale, and the 55-EDO degree representing the scale notes:
|
|
|
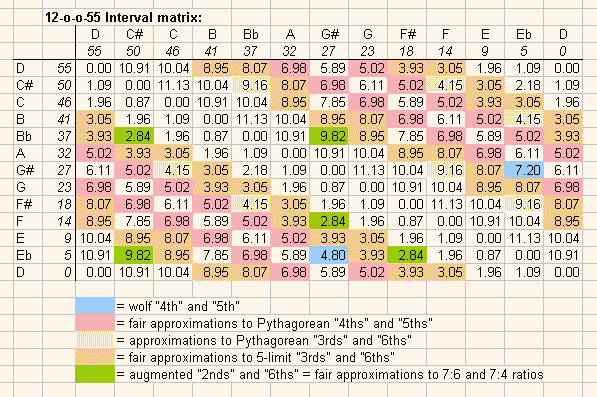
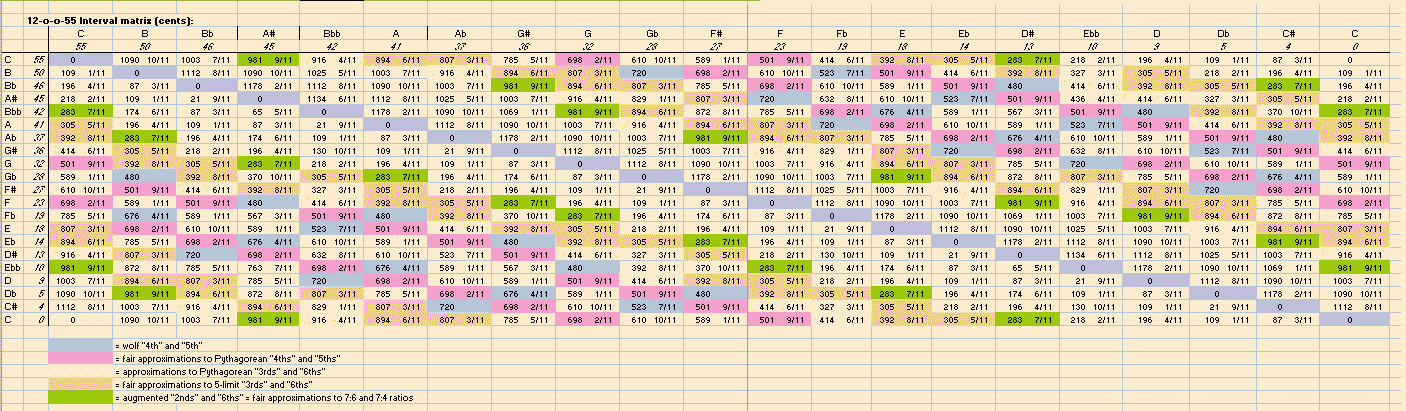
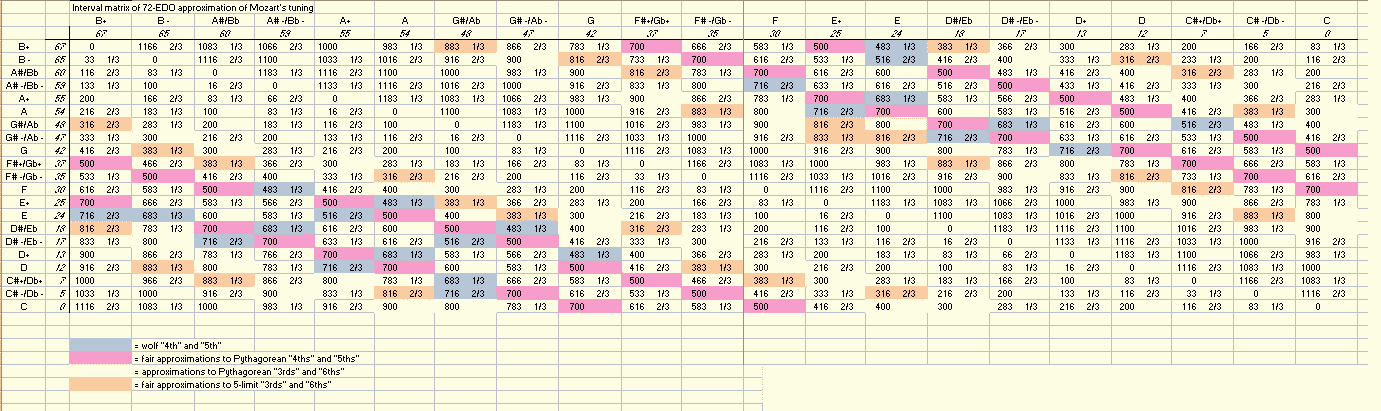
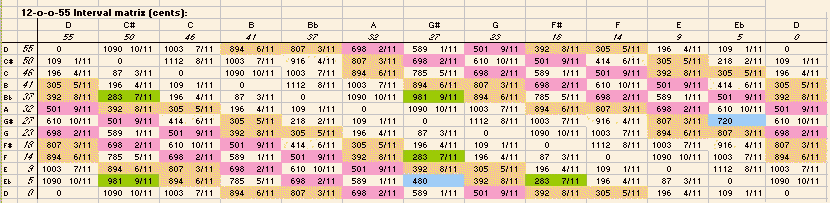
And last, the interval matrices for both tunings, showing the 55-EDO degrees for the 12-o-o-55 subset and the "cycle-of-5ths" value for the 1/6-comma meantone, with the Semitone values of all possible intervals given in the body of the table. Some important intervals are color-coded for easy recognition:
|
|
|
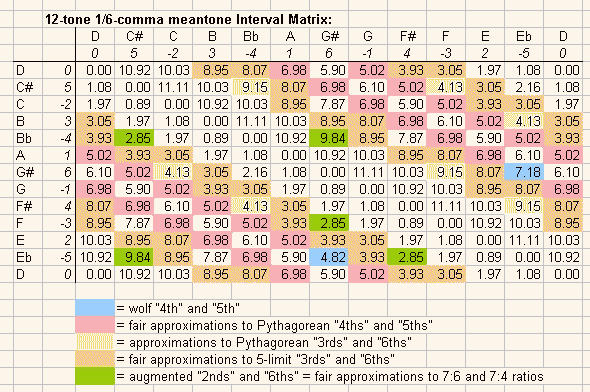
Here is the above table reproduced with fractional cents values instead of decimal Semitones:
Note also the following comment by Paul Erlich (from a Yahoo Tuning List post), echoing what Hind wrote at the end of his article:
There is no real evidence that Mozart intended 1/6- comma meantone rather than 1/5-comma or some other meantone system. It wouldn't make much sense for one to be that specific in regard to Mozart anyway, since he clearly assumes enharmonic equivalence even in a few passages for strings unaccompanied by keyboard, which violates his known violin teaching altogether.
REFERENCE
Chesnut, John Hind. 1977.
"Mozart's teaching of intonation",
Journal of the American Musicological Society
vol. 30 no. 2 [summer], pp. 254-271.