- the
ratio of two quantities
such that the smaller is to the greater, as the greater is to the
sum of the greater and the smaller:
where a < b : b / a = (a+b) / b ;
- one larger than its own reciprocal; thus by definition: ( 1 / F ) = ( F - 1 ) .
- the mean of quotients of adjacent elements in a series.
- Tom Dourado's
Golden Meantone Tuning
webpage for more information, including an exhaustive
table of interval data for a 31-tone golden meantone.
- Ron Knott's Phi page and his many other pages about Fibonacci and related numbers.
A tuning developed by Thorvald Kornerup and advocated by Jacques Dudon, this tuning is based on Phi, the golden mean (written with the Greek capital letter F "Phi") = (1 + 51/2) / 2 = ~1.61803398875
Phi is a unique constant. It is:
(Kornerup's calculations were actually based on ( F - 1 ), which mathmaticians call f "phi" in lower-case, and which Kornerup wrote as w, the lower-case of the Greek letter omega. Also, closely related to this topic is that of Fibonacci numbers, which form the integer terms of fractions which approximate F and f.)
This is a type of meantone composed of two different step sizes (designated L and s) such that 5L + 2s = one octave, as in many familiar diatonic scales. The "golden ratio" F comes into play in this tuning because it describes the ratio between log(s) and log(L) -- that is, the ratio between the perceived pitch-heights of s and L (and also of many other pairs of intervals in this tuning).
First we will set down the relationships for the most basic intervals, using only the data we already know here, and our knowledge of the usual number of meantone generators for the tone and semitone (L and s), then we will use algebra to derive the ratio for the generator, which is the tempered meantone version of the "perfect 5th", entirely in terms of the golden mean F, then we will use that value in calculating other intervals, including s and L.
Thus:
F = golden ratio = (1 + 5(1/2) ) / 2 s = diatonic semitone = t(1/F) = t(F-1) = 23/v5 t [= L] = tone = sF = v2/2 v = "5th" = t3 * s
So, t = sF is one suitable place to start.
t = sF
v2 ( 23 )F
= --- = (--- )
2 ( v5 )
v2 23F
= --- = ----
2 v5F
Multiply both sides by v5F :
v(5F+2)
------ = 23F
2
Multiply both sides by 2 :
v(5F+2) = 2(3F+1)
To solve for v, the exponent of 2 becomes the numerator of
a fraction, and the exponent of v becomes its denominator:
v = 2[(3F+1)/(5F+2)]
And that exponent of 2 can be simplified still further. Gene Ward Smith wrote (Yahoo tuning-math group message 2507 (Mon Jan 7, 2002 7:31 pm):
Ratios of the sort (a+br)/(c+dr) define an algebraic number field, which can always be put into the form of a sum of rational numbers times powers of a single algebraic number r. In this case, that results in(a+br)/(c+dr) = (ac+ad-bd + (bc-ad)r)/(c2+cd-d2)This form of the algebraic numbers in the field Q(r) is unique, since {1, r} are a basis for a vector space over the rationals Q; hence we can determine if two elements of Q(r) are the same by putting them both into this form.
If we rearrange the exponent of 2 (in the ratio for v) so that it reads (1+3F)/(2+5F), and plug the values a=1, b=3, c=2, d=5, and F=r, into Gene's equation, the resulting answer is (-8+F)/-11, which can be simplified to (8-F)/11.
Thus, the golden meantone generator or "5th" "v", has the ratio of
2[ (8 - F) / 11 ] = ~1.49503444952678 = ~696.214474 cents,and is composed of three Large (3L) plus one small note (s), i.e. (3L+s) = (~192.429*3) + (~118.928) = ~696.215 cents.
The golden meantone "5th" or generator is thus near the middle of the meantone spectrum, with an interval size only a tiny bit larger than the Woolhouse/Erlich "optimal" 7/26-comma meantone and a little smaller than 1/4-comma. (see the graph near the bottom of the meantone entry).
Expressed as a fraction-of-a-comma meantone, the golden meantone generator is nearly indistinguishable from that of 4/15-comma quasi-meantone:
--- prime-factor vector --- ~ratio ~cents
2 3 5
[ 1/15 -1/15 4/15 ] 1.495039213 696.2199903 4/15-comma quasi-meantone "5th"
- [ (8-F)/11 0 0] 1.49503445 696.214474 golden meantone "5th"
---------------------------------
[(15F-109)/165 -1/15 4/15 ] 1.000003186 0.005516352 = ~1/181 cent = < 1 midipu
Golden meantone is also audibly indistinguishable from
Woolhouse's 7/26-comma "optimal meantone":
--- prime-factor vector --- ~ratio ~cents
2 3 5
[ (8-F)/11 0 0 ] 1.49503445 696.214474 golden meantone "5th"
- [ 1/13 -1/13 7/26] 1.494991593 696.164846 7/26-comma meantone "5th"
-----------------------------
[(93-13F)/143 1/13 -7/26] 1.000028667 0.049627981 = ~1/20 cent = ~2 cawapus
Because F is such a special ratio, there
are many pairs of intervals in golden meantone which have this
relationship between their perceived sizes. Therefore, there
are many ways to solve the equations to find out what "v" is
in terms of F. Here are several others:
2[ (8F+1) / (13F+3) ], derived from v = t3 * s, a usual diatonic equation;which all reduce to 2[(8-F)/11].= 2[ (4F+3) / (7F+5) ], derived from m2 = #1F
(diatonic semitone = chromatic semitoneF ), which is (23/ v5) = (v7/ 24)F;= 2[ (2F-1) / (3F-1) ], derived from p4 = m3F which is (2 / v) = (22 / v3)F;
= 2[ (3-F) / (4-F) ], derived from m6 = p4F, which is (23/ v4) = (2 / v)F ,
Any meantone interval can be designated in the form 2a * vb , where v is the generator (2[(8-F)/11] in this case), b is the number of generators needed to produce the "8ve"-invariant form of that interval, and a is the amount of "8ves" that must be added or subtracted to fit it into the reference "8ve".
The ratio of any golden meantone interval can be calculated from this notation very simply, with the formula 2[([ b * (8-F) ] / 11 ) + a ], which simplifies to 2[ (8b + 11a - bF) / 11 ]
Below is a table of the 14 intervals resulting from -6 to +7 generators, with their simplified golden meantone ratios. A fuller description of the most important ones follows.
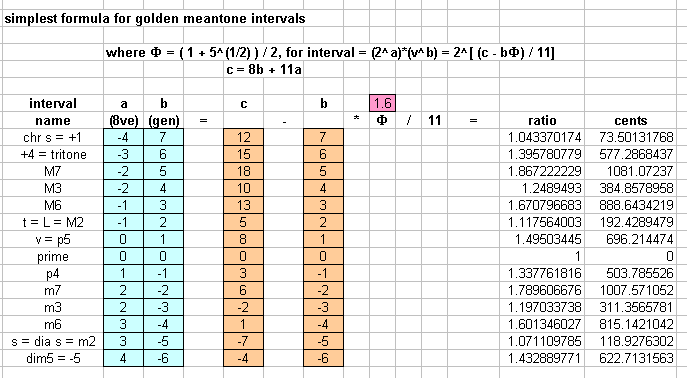
As with all meantones, the golden meantone
"major third" is
+4 generators minus 2 "8ves", or v4 / 22.
This has the ratio
2[([4*(8-F)]/11)-2]
= 2[(10-4F)/11]
= ~1.2489493 = ~384.8578958 cents.
The Large interval (L) is the "whole-tone"
(IInd), +2 generators minus one
"8ve" = v2 / 2 , with the
ratio
2[(5-2F)/11]
= ~1.117564003 = ~192.4289479 cents.
The small interval (s) is half the difference between 5 Large intervals
and one
"8ve", i.e. (8ve - 5L) / 2 ,
and is the
"minor 2nd" or "flat second"
(bIInd),
-5 generators plus 3 "8ves" = 23 / v5,
with the ratio
2[(5F-7)/11]
= ~1.071109785.
That is s = ~118.9276302 cents. This interval functions as the
diatonic semitone
in this tuning.
The
chromatic semitone
or "augmented prime" (aug1, #1, +1) is represented in meantone
as +7 generators minus 4 "8ves", or v7 / 24 .
In golden meantone its ratio is
2[(12-7F)/11]
= ~1.043370174 = ~73.50131768 cents.
EDOs which approximate
golden meantone to increasing degrees of accuracy are:
EDO degrees cents ~cents error from
of "5th" golden meantone
12 7 700 +3.785526045
19 11 ~694.7368421 -1.477631849
31 18 ~696.7741935 +0.559719594
50 29 696 -0.214473955
81 47 ~696.2962963 +0.081822342
131 76 ~696.1832061 -0.031267848
212 123 ~696.2264151 +0.01194114
555 322 ~696.2162162 +0.001742262
898 521 ~696.2138085 -0.000665491
(12edo lacks many of the features of golden meantone,
and is shown only for the sake of comparison.)
See also:
[from Joe Monzo, JustMusic: A New Harmony, with thanks to Tom Dourado and Gene Ward Smith.]
Updated:
2002.10.20 -- added comparison to EDOs and to 7/26-comma meantone
2002.1.13
2002.1.5-8 -- page created