12-eq is the abbreviation i formerly used for the usual and familiar 12-tone equal-tempered scale, the standard scale tuning used on keyboard, fretted string, and woodwind and brass instruments.
That abbreviation has been superceded in my work by the adoption of "12-EDO" or "12edo" generally, in cases where 12 equal divisions of the "octave" are considered to be a fundamental aspect of the tuning's musical usage, or by "12-tET" in the special circumstances where a temperament representing just-intonation is explicity intended.
The tuning is calculated by taking the twelfth root of each successive power
of 2, from 0 to 11; higher or lower
"octaves" of these 12 notes are
assumed to be, and are tuned as, equivalents. The 12th root of 2 can
also be written as
2(1/12), the next degree, the
12th root of 22, as 2(2/12), etc.,
the latter of each pair are
the way I normally write it on this website.
Any number to the 0th power equals 1, so the starting note of the scale, or 2(0/12), has the ratio 1:1.
Exponents which have numerators which are multiples of 12 form "octaves", as in the following:
| 2(12/12) | = | 21 | = | the ratio 2:1 | = | the "octave", |
| 2(24/12) | = | 22 | = | the ratio 4:1 | = | 2 "octaves", |
| 2(36/12) | = | 23 | = | the ratio 8:1 | = | 3 "octaves", |
These proportions, the origin and its octaves, are obviously all powers of 2. All other divisions in this scale are proportions known as irrational numbers.
As a result of the mathematical complexity, this scale was never tuned with absolute precision, with the exception of the "octaves" of the starting-note, until just a few decades ago, with the introduction of electronic and digital instruments and tuners. However, i speculate that as long ago as 3000 BC the Sumerians might have been able to calculate monochord string-lengths which approximated 12edo to such a high degree of accuracy that the two tunings would be audibly indistinguishable.
12edo arose historically by tempering out the
Pythagorean comma.
In a regular Pythagorean
chain of "pure" 5ths (with
the frequency
ratio 3:2), the
12th note in the cycle is nearly the same as the seventh
"octave" above or
below the starting note, differing by being wider by the
Pythagorean comma of ~24 cents. Distributing
this error among all 12 pitches, by
tempering the "5ths"
to make each one ~2 cents narrower than 3:2, eliminates the comma and
closes the cycle, so that the 12th note is now exactly the
same as the seventh "octave" of the starting note.
The tempering of the 12edo "5th" is calculated thus:
prime-factor vector
2 3 ratio cents
[-12/12 12/12] = 2-131 1.5 ~701.9550009 3:2 "pure 5th"
- [-19/12 12/12] = (2-19312)(1/12) ~1.001129891 ~1.955000865 1/12 Pythagorean comma
-----------------
[ 7/12 0 ] ~1.498307077 700 12edo "5th"
(1/12 of Pythagorean comma is also called a grad.)
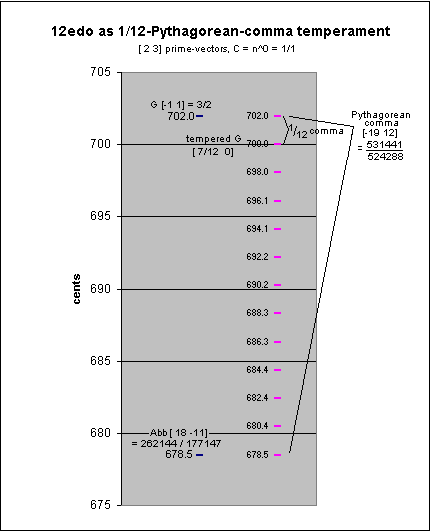
So the 12-EDO "5th", 2(7/12) = 7.00 Semitones = 700 cents, is ~1.955000865 cents narrower than the Pythagorean or just "5th" with the ratio 3:2 Expressed in fractions with increasing accuracy, this is 121/22, 164/67, or 185/89 cents narrow.
12-EDO may also be considered as both a
meantone and a
schismic tuning.
As with all meantones, 12-EDO maps the
"major 3rd"
to +4 generators,
and is indistinguishable from
1/11-comma meantone.
The 1/11-comma meantone "5th",
or generator, is
(3/2) / ((81/80)(1/11)) = ~ 699.9998836 cents:
prime-factor vector
2 3 5 ratio cents
[-11/11 11/11 0/11] = 2-131 1.5 ~701.9550009 3:2 "pure 5th"
- [ -4/11 4/11 -1/11] = (2-4345-1)(1/11) ~1.001129958 ~1.955117236 1/11 syntonic comma
------------------------
[ -7/11 7/11 1/11] ~1.498306976 ~699.9998836 1/11-comma meantone "5th"
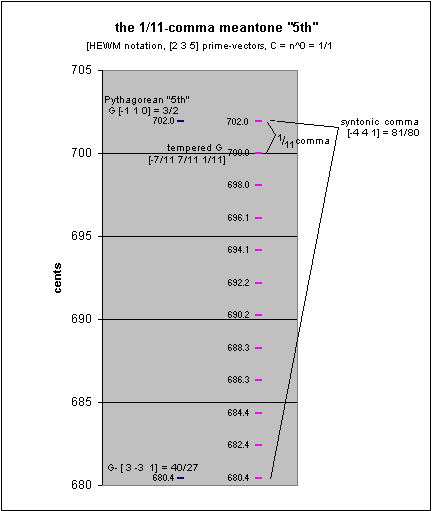
Interestingly, in 1/11-comma meantone, any two pitches
which are separated by 12 generators
are nearly identical, with only ~0.001396448
(~1/716) cent
between them; here is a typical example:
for C = n0 = 1/1 :
prime-factor vector
2 3 5 ratio cents
[ 43/11 -21/11 -3/11] ~1.189207355 ~300.0003491 1/11-comma meantone -3 generator: Eb
- [-118/11 63/11 9/11] ~1.189206396 ~299.9989527 1/11-comma meantone +9 generator: D#
-------------------------
[ 161/11 -84/11 -12/11] ~1.000000807 ~0.001396448
Thus, it becomes in effect a closed 12-tone meantone, and is in every respect identical to 12-EDO.
The difference between the two "5ths" is only ~1/8593 cent,
really a negligible difference:
prime-factor vector
2 3 5 ratio cents
[ 77/132 0/11 0/11] = [ 7/12 0 0 ] ~1.498307077 700 12edo 5th"
- [-84/132 7/11 1/11] = [-7/11 7/11 1/11] ~1.498306976 ~699.9998836 1/11-comma meantone "5th"
-----------------------
[161/132 -7/11 -1/11] ~1.000000067 ~0.000116371 difference between the two
12edo also functions as a
schismic tuning,
mapping the
"major 3rd"
to -8 generators.
The grad --
the amount the 12edo "5th" is
tempered narrow from the "pure"
Pythagorean "5th" --
happens to be nearly equal to the skhisma:
2 3 ~cents
[ -19/12 1] 1.955000865 tempering of 12edo "5th" = grad
- [-180/12 8] = [-15 8] 1.953720788 skhisma
---------------
[ 161/12 -7] 0.001280077 ~1/781-cent difference
(See Ellis's footnote * on p 316 of Helmholtz, On The Sensations Of Tone.)
Coincidentally, the amount of tempering of -8 generators (i.e., 8 "4ths" upward or 8 "5ths" downward) also happens to give the closest approximation to the "major 3rd" in 12edo, thus tempering out the skhisma.
Erv Wilson, in On the development of intonational systems by extended linear mapping (Xenharmonikôn 3, 1975), has noted that our familiarity with 12edo and its dual ability to map the "major 3rd", to both +4 and -8 generator "5ths", is advantageous in providing a path towards intonational expansion.:
The much maligned Cycle of 12 (and unjustly so) presents
that unique coincidence of events whereby may be effected a
remapping of the 5-function from the +4 linear position to
the -8 linear position. And we may be in the process of doing
that. It could not have happened in meantone. But the shift-
ing from meantone, which allows only the +4 mapping of the
5-function, to the cycle of 12, which also allows the -8
mapping; this, combined with practice, in one major school,
of avoiding 'diatonic patterns', that is, patterns where the
+4 mapping has any effective meaning, suggests that remapping
the 5-function to linear -8 is imminent. Likely it has already
occured, and both orders of mapping are competing for dominance.
This tuning is frequently abbreviated as 12-ET or 12tET by others.
[from Joe Monzo,
JustMusic:
A New Harmony]
updated
2002.09.22 -- added mathematical details and diagrams on Pythagorean tempering, meantone and schismic tuning
2002.02.07 -- added details on 1/11-comma meantone