Margo Schulter has a well-known fondness for medieval music and Pythagorean tunings, as well as for some exotic ETs (such as 17-tET), which she uses primarily to compose what she calls 'xeno-Gothic' music.

Recently, however, in Tuning List message 12989, she proposed what she calls a multi-prime neo-Gothic JI scale, consisting of 12 notes so that it can be easily mapped to a regular keyboard.

In another post, message 13027, she corrected an error in her keyboard mapping diagram, giving the scale as follows (I have modified her diagram somewhat, and simplified it by changing her cents-values into Semitones):

    392/363    147/121     4/3             196/121    56/33 
      1.33       3.37     4.98               8.35      9.16  
      f#         g#        bb                c#'       d+1'       
    /    \     /    \     /   \             /   \      /  \
  1.33  0.71 1.33  0.81 0.81 1.23        1.33  0.71 0.10  2.04
  /        \ /        \ /       \         /       \  /      \
 f          g          a          b      c'         d'        e'    f'
1/1        9/8       14/11      63/44   3/2       27/16     21/11  2/1
 0        2.04        4.18       6.21   7.02       9.06     11.19 12.00
     \/          \/         \/       \/       \/        \/       \/
     9:8       112:99      9:8     22:21      9:8      112:99   22:21
     2.04       2.14      2.04     0.81      2.04        2.14    0.81

(Margo pointed out that her earlier error gave the wrong cents-value for 21/11, and proceeded to give the correct value of 1119.463 cents in her text, but inadvertently made a typo in her diagram again and gave it as 1119.643 cents.

Also, Margo says this scale has 'two versions of D, one mapped to the usual "D" key of a 12-note keyboard and the other to the "Eb" key. These two keys provide pure fifths for G and A respectively...'. But this is not correct: the note d+1' (56/33) is a 4:3 'perfect 4th' above "a" (14/11), not a '5th'. The note e' (21/11) is a 'perfect 5th' above "a" (14/11).)

Here is a pitch-height graph showing the Semitone values of the notes in the scale:

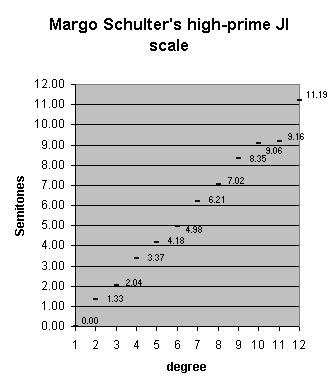
Margo noted some important features of the structure of this tuning as follows:

The basic idea of the tuning is to combine pure 3:2 fifths and 14:11 major thirds or ditones, the latter used as unstable but "relatively blending" intervals in neo-Gothic styles, much like the usual Pythagorean 81:64 of Gothic polyphony.

. . .

Here a crude lattice diagram, with an enthusiastic and appreciative invitation for more refined and sophisticated versions to the various exponents of this craft on the Tuning List, may be helpful.

Notes connected in horizontal rows form chains of pure 3:2 fifths, while diagonally connected major thirds (e.g. F0-A+1, E+1-G#+2) form pure 14:11 ratios, also expressible as the classic mediant between 5:4 and 9:7, or (5+9):(4+7).

     F#+2 -  C#+2  -  G#+2  
    /        /        /
   /        /        /
  D+1  -   A+1  -   E+1  -  B+1
 /        /        /        /
/        /        /        /
Bb0  -  F0   -   C0   -   G0   -  D0

She asked me both on the List and again in a private email if I would make a lattice diagram of this scale, according to my lattice formula. Here it is:

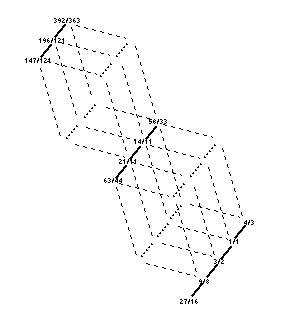
The lattice diagram clearly displays the features discussed by Margo, on which I elaborate further:

The prime-factors are 2 (not shown on this '8ve'-equivalent diagram), 3, 7, and 11. The prime-factor 5, which was especially important during a long period after that of Margo's main interest, is conspicuously absent. This feature also makes her scale a relative to many of those conceived by La Monte Young, who uses 3 and 7 a lot, and often many higher primes, but never 5.

The scale is clearly divided into 3 basic parts, all of which are chains of 3/2s ('perfect 5ths'). This is something which betrays Margo's primary interest in Pythagorean tunings. On the lattice, the pitches in each chain are connected by solid lines.

There are no direct connections between the chains of 3/2s along the 7 or 11 axes, both of these factors always being used together (i.e., the ratio 7/11 or 14/11) to connect pitches in two different chains. I have therefore used dashed lines to connect the chains of 3/2s, leaving blank spaces for the missing direct connections to 7¹ and 11^-1.

An interesting feature of Margo's scale , which she discusses in her Tuning List post, is that it uses 14/11 as exactly the kind of 'cross-exponent lattice connection' that I explored in detail in my Tuning List post message 2179 Sat Apr 3, 1999 00:14am. (Also see the small correction message 2190 Mon Apr 5, 1999 3:43am.) This is reflected very well in her own 'crude lattice diagram' above.

Here is a version of the lattice resembling my lattice formula but slightly different due to ASCII limitations. The lattice-points can be clicked to play a MIDI-file of that pitch:

      392:363 --------
       F#+2           /\
       /   \         /  \
   196:121 --------      \
    C#+2     \     /\     \
    /   \     \   /  \     \
147:121 --------      \     \
  G#+2    \     \\     \     \
     \     \      \-----\-- 56:33 ---------
      \     \   /  \     \   D+1           /\
       \     \ /    \     \ /   \         /  \
        \      --------- 14:11 ---------      \
         \   /        \   A+1     \     /\     \
          \ /          \ /   \     \   /  \     \
            --------- 21:11 ---------      \     \  
                       E+1     \     /\     \     \
                      /   \     \   / \\ ----\--- 4:3
                   63:44 --------     / \     \   Bb0
                    B+2     \     \\ /   \     \ /
                       \     \      \-----\--- 1:1
                        \     \    / \     \   /F0
                         \     \  /   \     \ /
                          \      ---------- 3:2
                           \    /       \   /C0
                            \  /         \ /
                              ---------- 9:8
                                         /G0
                                        /
                                     27:16
                                       D0
    
  

Margo sent the following commentary to me for inclusion here. I had noticed the point she makes here before she brought it to my attention, and meant to amend the webpage but forgot. I suppose it worked out better that way...

When Joe Monzo offered to make one of his famed lattice diagrams for my "multi-prime JI tuning" for neo-Gothic music, I was delighted; and indeed he has made the project his own, offering a fine presentation setting the tuning in a new perspective, as well as correcting a mistake on the size in cents of a major seventh which I managed to let slip in a "corrected" diagram of the tuning intended to "debug" exactly this point. Really, Monz has provided an introduction to this tuning that presents the main points maybe more effectively than I could.

However, while I was reading his Web page on this tuning, I did find one comment which made me remark to myself: "Isn't this an unlikely interpretation of what I was saying?" As it turns out, that "unlikely interpretation" is an opportunity for me not only to write what might be deemed a quibble upon a quibble, but to raise some points about fifths and fourths, pitch notations, octave affinity, and other matters often unexamined or taken for granted.

Here is the comment which provoked my acute interest, in the midst of my general delight with and admiration for the Web page:

Also, Margo says this scale has 'two versions of D, one mapped to the usual "D" key of a 12-note keyboard and the other to the "Eb" key. These two keys provide pure fifths for G and A respectively...'.

But this is not correct: the note d+1' (56/33) is a 4:3 [9] 'perfect 4th' above "a" (14/11), not a '5th'. The note e' (21/11) is a 'perfect 5th' above "a" (14/11).)

Here my initial and rather unreflective reaction might be to suggest that "obviously" I was referring not just to the one octave of the scale shown in the diagram but to any "pure fifths" D-A or G-D which might be formed in any applicable octaves of the gamut.

There is also a fine nuance of my pitch notation which might not be so obvious to an uninitiated bystander, or attentive lattice designer like the Monz for that matter.

When I wrote that "this scale has two versions of D" mapped to the "D" and "Eb" keys of a 12-note keyboard, in order to "provide pure fifths for G and A respectively," I used capital letters for the note names without any indications of specific octaves. To me, this implies that these generic letters represent what the 20th century sometimes calls "pitch classes," representing any occurrence of the given note in any octave. Thus one flavor of "D" forms "pure fifths" with a "G" immediately below it, the other with an "A" immediately above it.

In contrast, to specify octaves, I would use notations such as A3-D4 (ideal for most uses, but subject to possible confusion with comma notations in higher-prime JI settings) or a-d', either definitely showing a fourth up rather than a fifth down. If I had written "Here the version of d' mapped to the Eb key forms a pure fifth a-d' in the diagrammed octave," I would have indeed been clearly incorrect by my own standards.

Putting my somewhat defensive reaction at first blush aside, Monz invites some very interesting questions: Why do we seem more often to speak of pure fifths, or of a "chain of fifths," than of pure fourths or a chain of fourths?

In fact, in any regular "chain of fifths" tuning, or lineotuning as I call it, we often remark that all fifths have the same size. They are at a pure 3:2 in Pythagorean or 3-limit JI; somewhat smaller than 3:2 in meantones; and somewhat larger in neo-Gothic tunings such as 29-tet, 17-tet, or a lineotuning with pure 14:11 major thirds (very close to 46-tet).

However, we quickly find that the tuning chain for a given octave has not only fifths but fourths, and that these two kindred intervals must constantly alternate (e.g. fifths up or fourths down) if we wish to stay within the range of the octave.

Thus I might take Monz, quite apart from any interpretation of my ambiguous (and unexplained) pitch notation, as advocating equal opportunity for fourths. Let's consider the medieval context.

In the 13th century, the fifth (3:2) and fourth (4:3) are typically ranked together as "intermediate concords," being less purely blending than the simpler unison (1:1) and octave (2:1), but yet fully concordant, representing the ideal of rich and saturated stability.

In partnership, the more complex fifth and fourth together with the octave form the complete unit of three-voice sonority, the 3-limit trine (e.g. D3-A3-D4 or d-a-d'). The term trine comes from the Latin of Johannes de Grocheio (c. 1300), who wrote that this ideal three-voice sonority manifests trina harmoniae perfectio, a "threefold perfection of harmony."

While the fifth and fourth are ranked together in 13th-century theory, both in theory and practice the fifth is the more primary concord, the fourth ranking with-but-after the fifth. Jacobus of Liege (c. 1325), in his monumental Speculum musicae or "Mirror of Music," reflects this perspective when he asserts that the fourth is a concord in its own right, and in any position (below the fifth or above it), but that the fifth is the better concord, and ideally should be placed below the fourth rather than above (e.g. D3-A3-D4 in contrast to D3-G3-D4).

Thus my focus on "pure fifths" rather than fourths may reflect a certain 13th-century preference (or bias?) further exaggerated by many 14th-century and later theorists who argue that the fourth in itself should be treated as a kind of "dissonance," although between two upper voices it can serve as the concord which its simple 4:3 ratio might suggest. Interestingly, this was the view of certain "moderns" which Jacobus sought to refute in the early 14th century just when it was coming into vogue.

If we go back to the earliest recorded medieval Western European polyphony, however, we find that the fourth is often on parity with the fifth or even preferred as the primary consonance, the latter state of affairs holding in the Micrologus of Guido d'Arezzo (c. 1030), for example. About 300 years later, Jacobus defends the independently concordant status of the fourth in part by citing Guido's preferred style of diaphony for three voices, with the lower two voices moving in parallel fourths and a third voice placed at the octave above, thus arranging the fourth below and fifth above (e.g. C3-F3-C4, D3-G3-D4, etc.).

Incidentally, this dialogue also brings into play the question of octaves and octave affinity (a term I prefer to "equivalence," and a more qualified concept).

While fifths and fourths are kindred octave complements (two intervals together forming an octave), Monz's clear distinction between them reminds us that kindred intervals can yet have distinct qualities. In the 11th century, Guido prefers the simple fourth to the simple fifth, and places the fourth below the fifth; in the 13th century, converse preferences obtain.

Interestingly, in very recent as well as medieval theory, distinctions of this kind do definitely count. For example, just as 13th-century theorists find the ditone or major third (81:64) an "imperfect concord" (the mildest kind of unstable interval) but the semitone-plus-fifth (semitonium cum diapente) or minor sixth (128:81) as a quite strong discord often ranged with the minor second or major seventh. so 20th-century theorists may make a similar distinction between such octave complements as 11:7 and 14:11.

At least one theorist has concluded on the basis of experience that while 11:7 may be a "attractant" interval tuneable by ear, 14:11 is not recognizable as a distinct matching of partials. Paul Erlich's studies of "harmonic entropy" likewise emphasize that "octave equivalence" does not obtain in measuring what might termed the "sensory consonance" of various intervals and multi-voice sonorities.

The term "octave affinity" may be better: it notes the obvious similarity and relatedness of octaves and octave complements like the fifth and fourth, but leaves room for musically signficant distinctions as well. Guido compared the seven repeating note names of the diatonic scale to the repeating names of the days of the week (an "octave" also being a liturgical term for week, or "day a week after," as in "the Octave of Whitsunday"), but this musical "calendar" may have interesting asymmetries as well as symmetries.

At any rate, Monz's response to my inexact pitch notation can be taken as a very valuable bit of advocacy for those noble but oft-neglected fourths. Accordingly, I might revise my statement as follows:

This scale has 'two versions of D, one mapped to the usual "D" key of a 12-note keyboard and the other to the "Eb" key. These two keys provide pure fifths and fourths for G and A respectively in the various octaves of the gamut.

As always, Monz has brought his high craft and special viewpoint to the task of interpreting a tuning in a valuable and unique way, and at the same time promoted further inquiry and dialogue on often unexamined points.

Most appreciatively,

Margo Schulter