- Ivor Darreg
- Easley Blackwood
- Brian McLaren
- Marc Jones
- Dan Stearns
a system of tuning based on a scale whose "steps" or degrees have logarithmically equal intervals between them, in contrast to the differently-spaced degrees of just intonation, meantone, well-temperament, or other tunings. Generally abbreviated as ET.
Usually, but not always, equal temperaments assume octave-equivalence, of which the usual 12-EQ is the most obvious example. My preferred abbreviation for these types of temperaments is EDO, for which some other theorists substitute ED2; both of these specify that it is the 2:1 ratio which is to be equally divided.
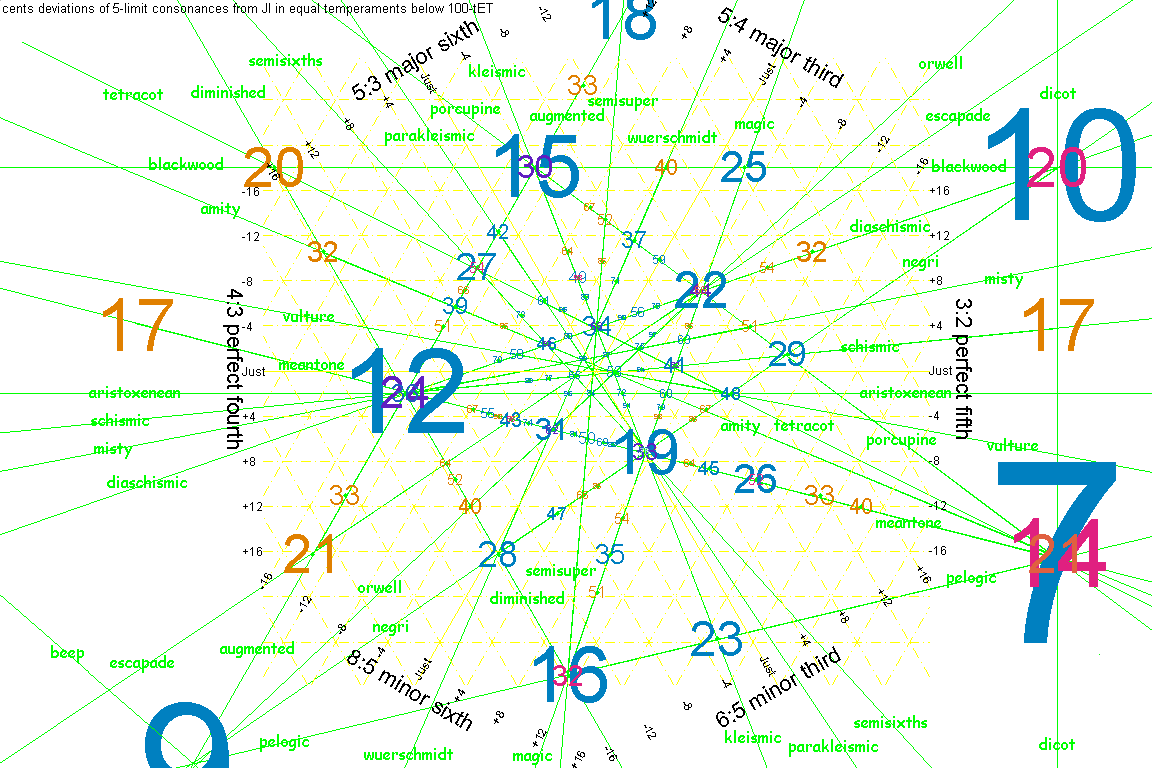
Below is a modification I made of a graphic by Paul Erlich, which shows the amount of error for various EDOs for the basic concordant intervals in the 5-limit.
The farther a point is from a given axis, the larger the errors in the tuning corresponding to the point, of the intervals corresponding to the axis.
The basic concept is the same as that of Dalitz plots in physics, and the Chalmers tetrachord plots (see diagrams #3 and #4 on that page).
LEGEND:
-
The blue lines represent
the just "perfect 5th"
and its "8ve"-complement the
"perfect 4th" (ratios 3:2 and 4:3),
and the just
"major 3rd / minor 6th" and
"minor 3rd / major 6th".
The red lines connect EDOs which are collinear on this graph. When this happens, it indicates that a certain important small interval acting as a unison-vector is being tempered out, which is also known as "vanishing".
Most of these red lines are labeled with the vanishing unison-vectors; some of them are labeled with names which may be consulted in this Dictionary for more information (meantone, syntonic comma, schismic, kleisma, MIRACLE, diaschisma, diesis).
A few of the ratios with the smallest terms are given, otherwise every unison-vector is designated by the matrix [x y z] of exponents of the prime-factors thus: 2x * 3y * 5z.
Below is a table listing each of the vanishing commas depicted in
the diagram above, and their associated temperaments. (Thanks
to Carl Lumma for the original version of this table.) Where the
name has "--" the temperament family has not yet been assigned a name,
and where it has "x" I also did not draw the red line on the diagram
because of lack of space.
comma name(s) {2 3 5}-vector num.:denom. cents temperament name(s) ETs heuristic complexity heuristic error
large limma [ 0 3 -2] 27:25 133.2375749 beep 4, 5, 9 3.295836866 38.90955906
classic chromatic semitone [ -3 -1 2] 25:24 70.67242686 dicot 3, 4, 7, 10 3.218875825 21.51352389
major limma, limma ascendant [ -7 3 1] 135:128 92.17871646 pelogic 7, 9, 16, 23 4.905274778 18.30023709
limma [ 8 -5 0] 256:243 90.22499567 blackwood 10, 15, 25 5.493061443 16.86080893
major diesis [ 3 4 -4] 648:625 62.565148 diminished, 'octatonic' 4, 12, 16, 28 6.43775165 9.89622099
maximal diesis [ 1 -5 3] 250:243 49.16613727 porcupine 7, 15, 22, 29, 37, 59 5.493061443 9.078897114
great diesis [ 7 0 -3] 128:125 41.05885841 augmented, diesic 3, 9, 12, 15, 18, 27, 39, 42 4.828313737 8.605409557
-- [ -14 3 4] 16875:16384 51.11985806 negri 9, 10, 19, 28, 29 9.733588516 5.175121053
syntonic comma [ -4 4 -1] 81:80 21.5062896 meantone 5, 7, 12, 19, 26, 31, 43, 45, 50, 55, 69, 74, 81, 88 4.394449155 4.863694883
small diesis [ -10 -1 5] 3125:3072 29.61356846 magic 3, 16, 19, 22, 25, 35, 41, 60, 63, 79 8.047189562 3.648693652
minimal diesis [ 5 -9 4] 20000:19683 27.65984767 tetracot 7, 27, 34 41, 48, 61, 75 9.887510598 2.819920032
diaschisma [ 11 -4 -2] 2048:2025 19.55256881 diaschismic, 5-limit pajara 12, 22, 34, 46, 56, 58, 70, 78, 80, 90 7.61332498 2.582761031
pythagorean comma [ -19 12 0] 531441:524288 23.46001038 aristoxenean 12, 48, 60, 72, 84, 96 13.18334746 1.767515597
-- [ 2 9 -7] 78732:78125 13.39901073 semisixths 19, 27, 46, 65, 73, 84 11.26606539 1.193939109
-- [ 26 -12 -3] 67108864:66430125 17.59884802 misty 12, 63, 75, 87, 99 18.0116612 0.982063908
wuerschmidt's comma [ 17 1 -8] 393216:390625 11.44528995 wuerschmidt 28, 31, 34, 37, 65, 71, 96, 99 12.8755033 0.891864646
kleisma [ -6 -5 6] 15625:15552 8.107278862 kleismic, hanson 15, 19, 23, 34, 53, 72, 83, 87, 91 9.656627475 0.837593197
semicomma [ -21 3 7] 2109375:2097152 10.06099965 orwell 9, 22, 31, 53, 75, 84, 97 14.56190225 0.688908734
-- [ 9 -13 5] 1600000:1594323 6.153558074 amity 39, 46, 53, 60, 99, 152 14.28195975 0.431628947
-- [ 32 -7 -9] 4294967296:4271484375 9.491569159 escapade 22, 43, 65, 87, 152 22.17522723 0.429201273
-- [ 8 14 -13] 1224440064:1220703125 5.291731873 parakleismic 19, 42, 61, 80, 99, 118, 217 20.92269286 0.25330523
schisma [ -15 8 1] 32805:32768 1.953720788 schismic, helmholtz/groven 29, 41, 53, 65, 77, 89, 118, 171 10.39833622 0.187781849
-- [ 24 -21 4] 10485760000:10460353203 4.199837286 vulture 48, 53, 58, 217, 323 23.07085806 0.18226178
-- [ 23 6 -14] 6115295232:6103515625 3.338011085 semisuper 16, 18, 34, 50, 84, 152, 270, 388 22.53213077 0.148287404
'19-tone' comma [ -14 -19 19] 1.90735E+13:1.90425E+13 2.81554699 enneadecal 19, 152, 171, 323, 494, 665 30.57932034 0.091998733
-- [ 39 -29 3] 6.87195E+13:6.86304E+13 2.246116498 tricot 53, 388, 441, 494, 547 31.85975637 0.070545869
-- [ -68 18 17] 2.96E+20:2.95E+20 2.523151279 vavoom 118, 547, 665 47.13546571 0.053490795
-- [ 38 -2 -15] 2.74878E+11:2.74658E+11 1.384290297 semithirds 118, 323, 441, 559 26.33879326 0.052578107
ennealimmal comma [ 1 -27 18] 7.62939E+12:7.6256E+12 0.861826202 ennealimmal 171, 441, 612 29.66253179 0.029061604
-- [ -16 35 -17] 5.00315E+16:5.0E+16 1.091894586 minortone 171, 388, 559, 730, 901 38.4514301 0.028387769
-- [ -53 10 16] 9.01016E+15:9.0072E+15 0.569430491 kwazy 118, 494, 612, 1342 36.73712949 0.015497587
-- [ 91 -12 -31] 2.47588E+27:2.47472E+27 0.814859805 astro 118, 1171, 2224 63.07639343 0.012915578
-- [ 37 25 -33] 1.1645E+23:1.16415E+23 0.522464095 whoosh 441, 730, 1171 53.1117529 0.009835587
monzisma [ 54 -37 2] 4.5036E+17:4.50284E+17 0.29239571 monzismic 53, 559, 612, 665, 1171, 1783 40.64882358 0.007192607
-- [ -36 -52 51] 4.44089E+35:4.44002E+35 0.339362106 egads 1342, 1783, 3125 82.08133353 0.004134056
-- [-107 47 14] 1.62285E+32:1.62259E+32 0.277034781 fortune 612, 1901, 2513, 3125 74.16690834 0.003734989
-- [ -17 62 -35] 3.8152E+29:3.8147E+29 0.230068385 senior 1171, 1342, 2513, 3684 68.1139619 0.003377473
-- [ 144 -22 -47] 2.23007E+43:2.22976E+43 0.245429314 gross 118, 1783, 1901, 3684 99.813194 0.002458712
-- [ -90 -15 49] 1.77636E+34:1.77631E+34 0.046966396 pirate 1783, 2513, 4296 78.86245771 0.00059554
-- [ 71 -99 37] 1.71799E+47:1.71793E+47 0.062327326 raider 1171, 4296 108.7626526 0.000573048
-- [ 161 -84 -12] 2.923E+48:2.92298E+48 0.015360929 atomic 3684, 4296 111.5966961 0.000137646
Below is a lattice diagram of these "vanishing commas". I have included all the ones listed in the table above except the two that plot the furthest away from the central 1/1 reference pitch: [10 -40 23] and [-11 26 -13]. I have labeled the ones that have names in current use among tuning theorists, and drawn vectors for a few of the others. (Compare this diagram with those on my webpage 5-limit intervals, 100 cents and under: they are essentially identical, except for the reversed orientation of prime-factors 3 and 5. Also see the lattice diagrams on the individual pages linked in the table.)
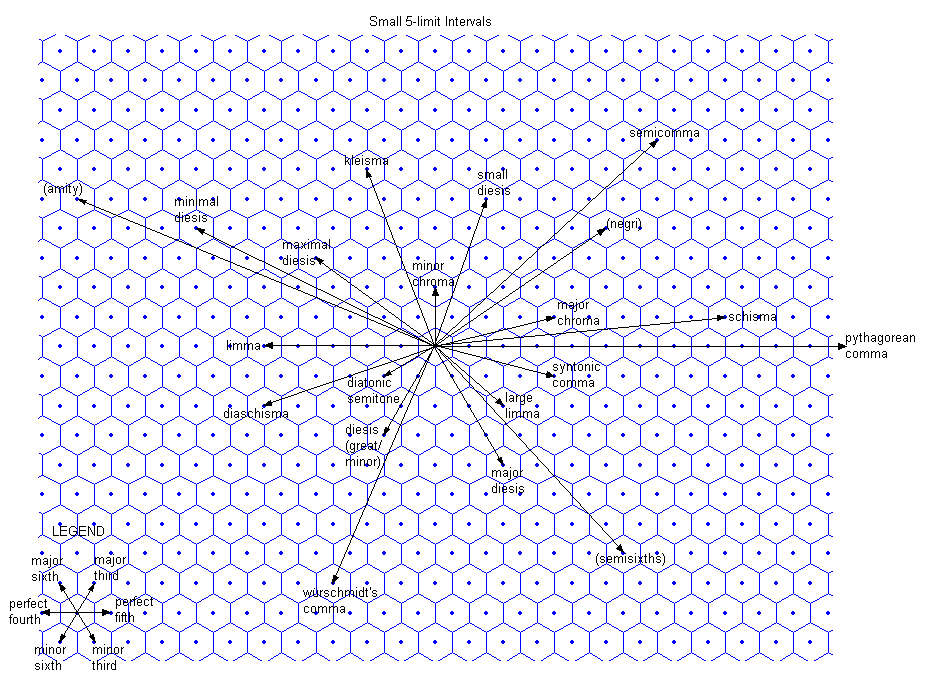
It's my belief that the vectors of these intervals play a role in the patterns of shading and coloring in the gallery of lattices below. Those lattices have the 3 and 5 axes oriented exactly as here.
Examples of non-octave equal temperaments are Gary Morrison's 88CET (88 cents between degrees), the Bohlen-Pierce scale, and Wendy Carlos's alpha, beta, and gamma scales [listen to them here].
In a post to the Early Music list, Aleksander Frosztega wrote:
P.S. [quoting] >The phrase "equal temperament" has existed in print since 1781<
French used the term "temperament egal" long before 1781.
The Germans used the phrase "gleichschwebende Temperatur" to denote equal-beating temperament since the beginning of the 18th century. This is not to be confused with equal-temperament, and instead actually denotes certain meantones, well-temperament, and other tunings where the varying temperings of different intervals results in them having equal numbers of beats per second.
Below is a table showing advocates of various "octave"-based ETs, with approximate dates. It does not claim to be complete, and keeps growing. (click on the highlighted numbers to show more detail about those ETs)
NOTE:
-
The following composers have written in so many different
equal-temperaments that they will (eventually) each have their own page:
| ET | Date and Theorist/composer |
| 5 | some theorists describe Indonesian slendro scale as this
2001 Herman Miller |
| 6 | the "whole-tone scale"
1894 Claude Debussy 1902 Arnold Schönberg |
| 7 | traditional Thai music
1991 Clem Fortuna 1997 Randy Winchester 2001 Robert Walker |
| 8 | 1980 Gordon Mumma (Octal Waltz for harpsichord)
1981 Daniel Wolf 1997 Randy Winchester |
| 9 | early 1900s Charles Ives (in Monzo analysis of Ives "stretched" scales
1930s-60s R. M. A. Kusumadinata (Sunda: mapping of 3 pathet onto 7-out-of-9-equal) 19?? James Tenney (piano part, The Road to Ubud) |
| 10 | 1930s-60s R. M. A. Kusumadinata (Sunda)
1990s Elaine Walker 1978 Gary Morrison 1997 Randy Winchester 1998 William Sethares |
| 11 | 1996 Daniel Wolf |
| 12 | before 3000 BC a possible Sumerian tuning (according to speculations by Monzo)
1584 Prince Chu Tsai-yü 1585 Simon Stevin 1636 Marin Mersenne 1802 Georg Joseph Vogler 1817 Gottfried Weber 1900-1999 the predominant tuning of the 'developed' world 1911 Arnold Schönberg (along with his personal rejection of microtonality) |
| 13 | 1962 Ernst Krenek (opera Ausgerechnet und Verspielt, op. 179)
1991 Paul Rapoport 1998 Herman Miller 1999 Dan Stearns 2001 X. J. Scott |
| 14 | 19?? Ralph Jarzombek
2000 Herman Miller |
| 15 | 1930s-60s R. M. A. Kusumadinata (Sunda)
1951 Augusto Novaro 1983 Joe Zawinul, with the group Weather Report 1991 Easley Blackwood 1991 Clem Fortuna 1996 Herman Miller 1997 Randy Winchester 1998 Paul Erlich, with the group MAD DUXX 2001 Francesco Caratozzolo |
| 16 | 1930s-60s R. M. A. Kusumadinata (Sunda)
1971 David Goldsmith 1993 Steve Vai 1997 Randy Winchester 1998 Herman Miller |
| 17 | 1653 Brouncker
1809 Villoteau (describing Arabic tuning) 1929 Malherbe 1935 Karapetyan 1960s Ivor Darreg 1997 Herman Miller 1999 Margo Schulter (as a pseudo-Pythagorean tuning) |
| 18 | 1907 Ferrucio Busoni (in his theory, but not used in his compositions)
1960s Ivor Darreg |
| 19 | 1558 Guillaume Costeley
1577 Salinas (19 notes of '1/3-comma meantone', almost identical to 19-ET) before 1633 Jean Titelouze ('third-tones' may describe 19-ET) 1835 Wesley Woolhouse (the most practical approximation of his 'optimal meantone') 1852 Friedrich Opelt 1911 Melchiorre Sachs 1921 José Würschmidt 1922 Thorwald Kornerup 1925 Ariel 1926 Jacques Handschin 1932 Joseph Yasser 1940s Tillman Schafer 1961 M. Joel Mandelbaum 1960s Ivor Darreg 1979 Yunik & Swift 1979 Jon Catler 19?? Matthew Puzan 198? Erik Griswold 1987 Herman Miller 1996 Neil Haverstick 1990s Elaine Walker 1990s Jonathan Glasier 1990s Bill Wesley 1998 Joe Monzo |
| 20 | 1980 Gerald Balzano
1996 Paul Zweifel 1999 Herman Miller |
| 21 | 2001 Herman Miller |
| 22 | (some older theories describe the Indian sruti system as this)
1877 Bosanquet 1921 José Würschmidt (for the future, after 19 runs its course) (1960s Erv Wilson -- used modulus-22, not necessarily ET) 1960s Ivor Darreg 1980 Morris Moshe Cotel 1993 Paul Erlich 1997 Steve Rezsutek -- customized guitars and a keyboard for Paul Erlich's 22edo scales 1997 Randy Winchester 1999 Herman Miller 2000 Alison Monteith |
| 23 | some theorists describe Indonesian pelog scale as subset of this
1920s Hornbostel (describing Burmese music) |
| 24 | 21 (= 2) units per Semitone = 12 * 21 units per "octave".
1906 Richard H. Stein (first published 24-tET scores) 1908 Arnold Schönberg (sketches, no longer extant) 1908 Anton Webern (sketches) 1916 Charles Ives 1917 Willi von Möllendorff 1918 Jörg Mager 1920 Alois Hába (and subsequently many of his students) 1924 Julián Carrillo 1932 adopted as standard tuning in Egypt and elsewhere in Arabic world 1933 Ivan Wyschnegradsky (Treatise on Quartertone Harmony) 1941 Mildred Couper 1948 Pierre Boulez (original version of Le Soleil des Eaux) 1950s Giacinto Scelsi (very loosely-conceived intonation) 1967 Tui St. George Tucker 1969 Györgi Ligeti (Ramifications) 1960s-2000s John Eaton 1980s Brian Ferneyhough (very loosely-conceived intonation) 1983 Leo de Vries 1994 Joe Monzo |
| 25 | 1994 Paul Rapoport |
| 26 | 1998 Paul Erlich
1998 Herman Miller |
| 27 | 2001 Gene Ward Smith
2001 Herman Miller |
| 28 | 1997 Paul Erlich (for music based on the diminished scale) |
| 29 | 18?? Émile Chevé (by mistake) |
| 31 | 1555 Nicola Vicentino (31 notes of extended meantone nearly identical to 31-ET)
1606 Gonzaga (31 notes of extended meantone nearly identical to 31-ET) before 1618 Scipione Stella (31 notes of extended meantone nearly identical to 31-ET) 1618 Fabio Colonna (31 notes of extended meantone nearly identical to 31-ET) 1623 Daniel Hizler (used only 13 out of 31-ET in practice) 1666 Lemme Rossi 1691 Christiaan Huygens 1722 Friedrich Suppig 1725 Ambrose Warren 1739 Quirinus van Blankenburg (as a system of measurement) 1754 J. E. Gallimard 1818 Pierre Galin 1860s Josef Petzval 1917-19 P. S. Wedell (quoted by Kornerup) 1930 Thorvald Kornerup 1932 Joseph Yasser (for the future, after 19 runs its course) 1941 Adriaan Fokker 1947 Mart. J. Lürsen 1950s Henk Badings (and many other Dutch composers) (1960s Erv Wilson used modulus-31, not necessarily ET) 1962 Joel Mandelbaum 1967 Alois Hába 1970s Dr. Abram M. Plum 1973 Leigh Gerdine 1974 Sebastian von Hörner 1975 George Secor 1979 Jon Catler 1980s Brian Ferneyhough (very loosely-conceived intonation) 1989 John Bischoff and Tim Perkis 1999 Paul Erlich |
| 34 | 1979 Dirk de Klerk
before 1998 Larry Hanson 1997 Neil Haverstick |
| 36 | 3 units per Semitone = 12 * 3 units per "octave".
1907 Ferrucio Busoni (in his theory, but not used in compositions) 1923-1960s Alois Hába |
| 41 | 1901 Paul von Jankó
(1960s Erv Wilson claims that Partch was intuitively feeling out 41-ET) 1975 George Secor 1989 Helen Fowler 1998 Patrick Ozzard-Low |
| 43 | 1701 Joseph Sauveur meride (nearly identical to 1/5-comma meantone) |
| 46 | 1989 R. Fuller
1998 Graham Breed 2000 Dave Keenan and Paul Erlich |
| 48 | 22 (= 4) units per Semitone = 12 * 22 units per "octave".
early 1900s Charles Ives (in Monzo analysis of Ives "stretched" scales 1915 N. Kulbin 1924 Julián Carrillo 19?? Patrizio Barbieri 19?? Claus-Steffen Mahnkopf 19?? Volker Staub 1998 Joseph Pehrson |
| 50 | (nearly identical to 2/7-comma meantone, the first meantone to be
described with mathematical exactitude, in 1558 by Zarlino)
1710 Konrad Henfling 1759 Robert Smith (as an approximation to his ideal 5/18-comma meantone system) 1835 Wesley Woolhouse (almost identical to his 7/26-comma 'optimal meantone') 1940s Tillman Schafer |
| 53 | (nearly identical to both Pythagorean and 5-limit JI tuning)
400s BC Implied by Philolaus (disciple of Pythagoras) 200s BC King Fang 1608 Nicolaus Mercator (only as a system of measurement, not intended to be used on an instrument) 1650 Athanasius Kircher (1713 53-tone Pythagorean tuning became official scale in China) 1874-75 R. H. M. Bosanquet 1875 Alexander J. Ellis (appendix to Helmholtz, On the Sensations of Tone) 1890 Shohé Tanaka c.1900 Standard Turkish music-theory 1911 Robert Neumann (quoted by Schönberg in Harmonielehre) |
| 55 | (nearly identical to 1/6-comma meantone)
1711 Joseph Sauveur, "the system which ordinary musicians use" before 1722 Johann Beer 1723 Pier Francesco Tosi before 1748 Georg Philip Telemann 1748 Georg Andreas Sorge 1752 Johann Joachim Quantz 1755 Estève 1780s W. A. Mozart, subsets of up to 20 tones, for non-keyboard instruments (according to Monzo) |
| 58 | 1770 Dom François Bedos de Celles
2002 Gene Ward Smith |
| 60 | 5 units per Semitone = 12 * 5 units per "octave".
1980s? Richard Boulanger |
| 68 | 1847 Meshaqah (describing modern Greek tuning)
1989? John Chalmers (describing Byzantine tuning) |
| 72 | 6 units per Semitone = 12 * 6 units per "octave".
1800s standard quantization for Byzantine Chant 1927 Alois Hába (in his book Neue Harmonielehre) 1938-58 Evgeny Alexandrovich Murzin created a 72-tET synthesizer. Among composers to write for it: Andrei Volkonsky, Nikolai Nikolsky, Eduard Artemiev, Alexander Nemtin, Andrei Eshpai, Gennady Gladkov, Pyotr Meshchianinov, Stanislav Kreichi (see Anton Rovner's article in TMA). 1951 Augusto Novaro 1953 Ivan Wyschnegradsky 1963 Iannis Xenakis (cf. his book Musiques formelles) 1970 Ezra Sims 1970 Franz Richter Herf 1970 Rolf Maedel 1970s? Joe Maneri (and subsequently many of his students) 1980s? James Tenney 1990s Ted Mook 1999 Paul Erlich 1999 Joe Monzo (as basis of simplified HEWM notation) 1999 Rick Tagawa 2001 Dave Keenan, Graham Breed, Joseph Pehrson, Paul Erlich, Joe Monzo (as superset and for notation of MIRACLE subset scales) 2001 Julia Werntz |
| 74 | 1762 Riccati (approximation to 3/14-comma meantone)
1855 Drobisch (approximation to 2/9-comma meantone) 1991 John Cage, in "Ten" for chamber ensemble |
| 76 | 1998 Paul Erlich (as a unified tuning for various tonal systems) |
| 84 | 7 units per Semitone = 12 * 7 units per "octave".
1985 Harald Waage (for 5-limit JI) |
| 96 | 23 (= 8) units per Semitone = 12 * 23 units per "octave".
1924 Julián Carrillo 1980 Pascale Criton 2001 Vincent-Olivier Gagnon |
| 100 | 1980s Barry Vercoe - built into CSound software |
| 118 | 1874-5 Bosanquet |
| 144 | 12 units per Semitone = 12 * 12 units per "octave".
1946 Joseph Schillinger 1999 Dan Stearns and Joe Monzo (chiefly for its value as a unified notation for mixed EDOs and/or complex JI tunings) |
| 152 | 1999(?) Paul Erlich, "Universal Tuning" |
| 171 | 1926 Perrett
1975 Martin Vogel |
| 200 | 16 2/3 degrees per Semitone
2002 Joe Monzo (in analyzing Werckmeister III) |
| 205 | 2001 Aaron Hunt: 205 = 41 x 5 = [(7 x 6) - 1] x 5 = (12 x 17) + 1 |
| 217 | 7 * 31 degrees per octave = 18 1/12 degrees per Semitone
2002 Joe Monzo (for adaptive-JI tuning of Mahler's compositions) 2002 Bob Wendell (for quantification of JI to facilitate composing in a polyphonic blues style) 2002 George Secor & Dave Keenan (as a basis for notation for JI and multi-EDOs) |
| 270 | 1970s? Erv Wilson and John Chalmers
1997 Paul Hahn |
| 288 | early 1900s Charles Ives (in Monzo analysis of Ives "stretched" scales |
| 300 | 25 units per Semitone = 12 * 25 units per "octave".
1800s system of savarts |
| 301 | 1701 Joseph Sauveur heptameride (for ease of calculation with logs: log(2)~=0.301; and because 301 is divisible by 43)
before 1835 Captain J. W. F. Herschel (cited by Woolhouse) |
| 318 | 1999 Joe Monzo (in analyzing Aristoxenus; 318 = 53*6) |
| 512 | 29 units per "octave".
1980s tuning resolution of some electronic instruments, notably Ensoniq VFX and VFX-SD. |
| 612 | 51 (= 3 * 17) units per semitone = 22 * 32 * 17 units per "octave"
before 1875 Captain J. W. F. Herschel (cited by Bosanquet) c.1970 Gene Ward Smith (for interval measurment, his analogue of cents) 2002 Joe Monzo (in analyzing Werckmeister III) |
| 730 | 1835 Wesley Woolhouse (his unit of measurement and an analogue of cents; 60 5/6 degrees per Semitone.) |
| 768 | 1990s Tuning resolution of many electronic instruments, including several by Yamaha, Emu, and Ensoniq, which provide 26 (= 64) pitch-bend units per semitone: 768 = 12 * 26. |
| 1000 | millioctave, an interval measurement, an analogue of cents: 1000 = 23 * 53 = 83 1/3 units per Semitone.
1993 Mark Lindley (in his book Mathematical Models of Musical Scales) |
| 1024 | 210
(= 1024) units per "octave" = 85 1/3 units per Semitone; an analogue of cents.
1980s Tuning resolution for many synthesizers with tuning tables, including the popular Yamaha DX, SY and TG series 1990-95 Joe Monzo (tuning resolution of my Yamaha TG-77) |
| 1060 | date-? standard Turkish music-theory (1060 = 53 * 20, their analogue of cents) |
| 1200 | 1875 Alexander Ellis (his unit of measurement, called cents, 100 per 12-tET semitone) |
| 1536 | 27 = 128 units per Semitone; 12 * 27
= 1536 units per "octave"; pitch-bend resolution of some sequencer software, including Texture.
1980s Joe Monzo (using Texture) |
| 1728 | 19??- Paul Beaver (rendered as 123) |
| 3072 | 1990s Apple's QuickTime Musical Instruments spec, 28 (= 256) units per Semitone = 12 * 28 units per "octave". |
| 49152 | 1980s cawapu, MIDI pitch-bend unit used in CakewalkTM and other popular sequencer programs, 212 (= 4096) units per 12-tET Semitone = 12 * 212 units per "octave". |
| 196608 | 1980s midipu, finest resolution suggested in the MIDI tuning Spec, 214 (= 16384) units per 12-tET Semitone = 12 * 214 units per "octave". |
Note that Easley Blackwood's Microtonal Etudes contain one etude for each ET from 13 thru 24, and that Ivor Darreg (in the 1970s and 80s) and Brian McLaren (in the 1990s) composed pieces for every ET between 5 and 53, and Dan Stearns and Marc Jones (in the 1990s and 2000s) have composed in numerous different ETs, often mixing several of them in the same piece. |
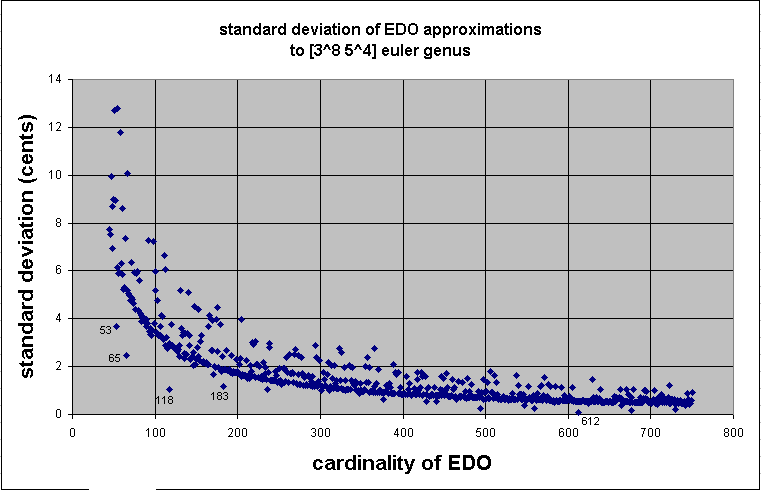
Below is a graph showing the standard deviation (in
cents)
from the ratios in the
euler genus lattice
with the arbitrarily chosen boundaries
3(0...+8) * 5(0...+4),
for all EDOs from 45 to 750.
The best EDO representations of this
5-limit
lattice are labeled:
53-, 65-, 118-, 183-, and 612-edo.
Below are lattice diagrams
showing the amount of error of
various EDOs from
5- (and in some cases 7- and 11-)limit
JI,
in which I've used greyscale to show the amount of
error from the just ratio.
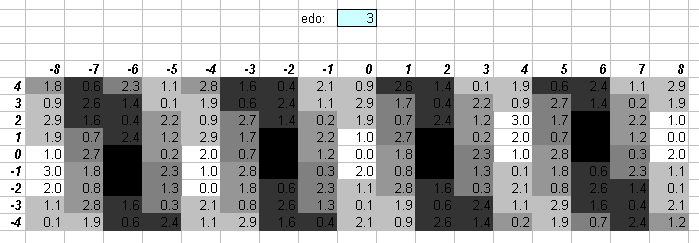
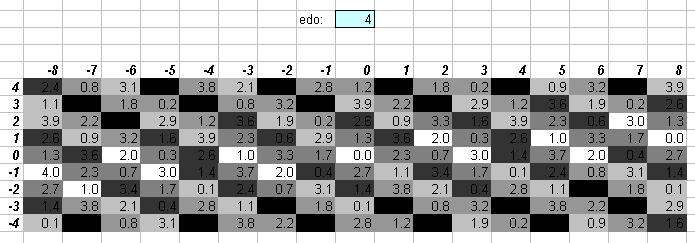
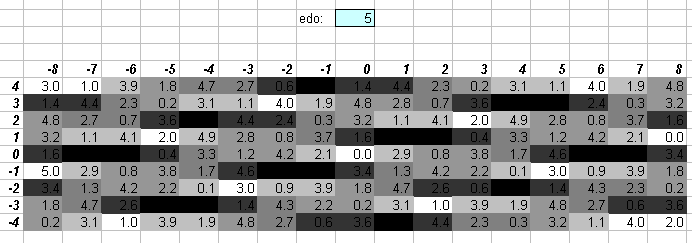
Prime-factor 3 is along the horizontal axis, and prime-factor 5 is along the vertical. In those cases where I illustrate lattices for prime-factors higher than 5, the format resembles the old method I used to use (as in several lattices in my book) wherein prime-factors 3 and 5 form a grid, which is then replicated for various exponents of the other primes, somewhat like a ladder.
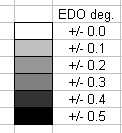
The numbers in the central cells show the degree of the EDO which most closely approximates the ratio, and is given to one decimal place. The actual EDO degree is the integer part of that value, and the amount of error is given here to one decimal point as 1/10 of a degree in that EDO.
I deliberately give the error in terms of EDO degrees rather than in a typical reference measurement such as cents, so as to use a perspective which emphasizes the qualities of the particular EDO, in an attempt to quantify Ivor Darreg's postulate that each EDO has its own mood (see Darreg 1986, New Moods).
If the decimal part is zero, the cell is white. If the decimal part is .1 or .9, the cell is the lightest shade of grey. If the decimal part is .2 or .8, the cell is the next darker shade of grey; .3 or .7, the next darker shade of grey; .4 or .6, the darkest shade of grey, and if it is .5, the cell is black since that ratio can be equally well approximated by the EDO degree on either side of that value. Here is the legend, with error given as a fraction of an EDO degree:
The patterns of shade shown on these lattices show interesting correspondences with other lattices I've made. See, for instance, my webpage Lattice diagrams comparing rational implications of various meantone chains, and compare the 19edo lattice here with the 1/3-comma meantone lattice on that page; compare 43edo here with 1/5-comma there, and 12edo here with 1/11-comma there.
For some EDOs I also give a color lattice to show whether the tempering of a particular interval is positive or negative. This may show that certain pairs of temperaments which look very similar on the greyscale lattice are actually "opposites" in a sense, because one is a positive system and the other a negative. (Example 1: the diagram of 22edo resembles that of 43edo, but they are in fact very different tunings, because 22 is positive and 43 is negative; example 2: 19 and 34 look similar, but 19 is negative and 34 is positive.) I used shades of blue to represent pitches which the EDO gives as too flat (negative tempering), and shades of orange to represent EDO pitches which are too sharp (positive tempering), and dark grey for those JI pitches which fall right between two of the EDO degrees. Here is the legend, with error given as a fraction of an EDO degree:
[Note: Herman Miller's Warped Canon page has MIDI versions of Pachelbel's Canon in most of the tunings listed here, and several others as well.]
3edo
3edo is the subset of 12edo which forms the "augmented triad".
4edo
4edo is the subset of 12edo which forms the "diminished 7th tetrad".
5edo
5edo is the lowest cardinality EDO which provides something recognizable as a scale. In this case, it is a form of the pentatonic scale, but without anything resembling "3rds". One degree of 5edo (exactly 240 cents) is fairly close to 144:125 = [2 3 5]^[4 2 -3] (= ~244.9689 cents).
6edo
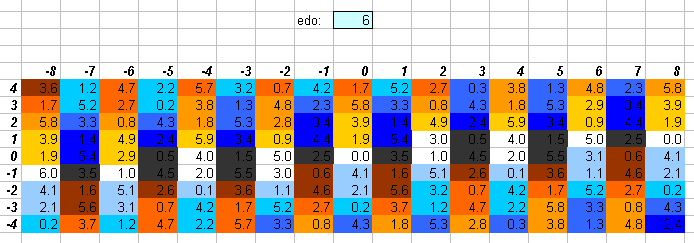
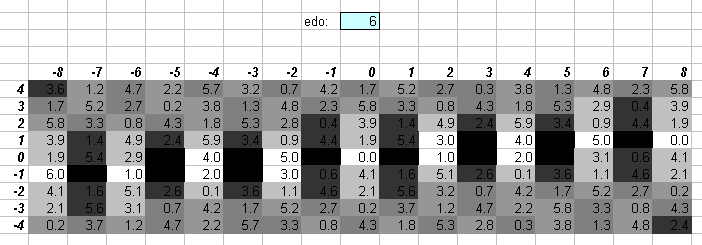
The "whole-tone" scale, used prominently around 1900 by Debussy and Schoenberg as a subset of 12edo. One degree of 6edo (exactly 200 cents) is quite close to the Pythagorean "whole-tone" 9:8 = [2 3 5]^[-3 2 0] (= ~203.91 cents).
7edo
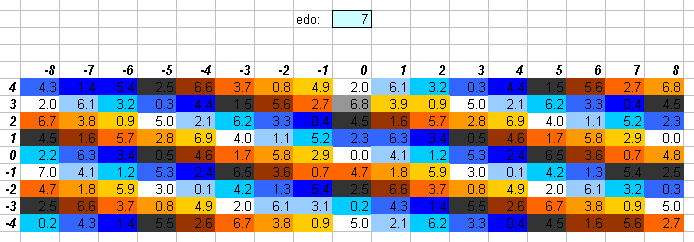
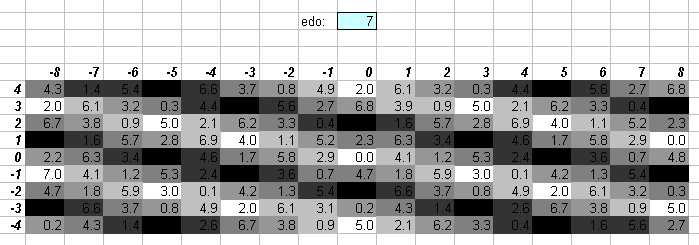
The closest 7edo approximation to the "perfect 5th" 3:2 is 4 degrees of 7edo. The fact that this is slightly narrower than the 3:2 ratio makes it a negative system, causing it to resemble a meantone generator, and makes 7edo the lowest cardinality EDO which may represent the meantone family of temperaments, except for the fact that the scale produced by 7edo contains "3rds" which are "neutral" (i.e., neither "major" nor "minor").
8edo
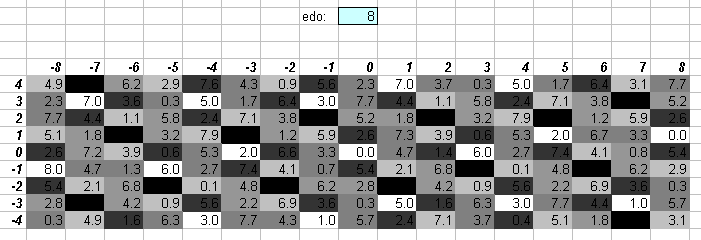
Note that 8edo is available as a subset of 72edo.
9edo
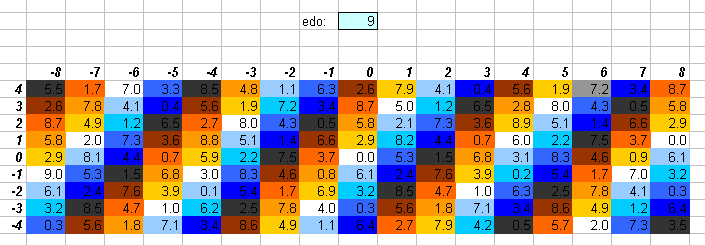
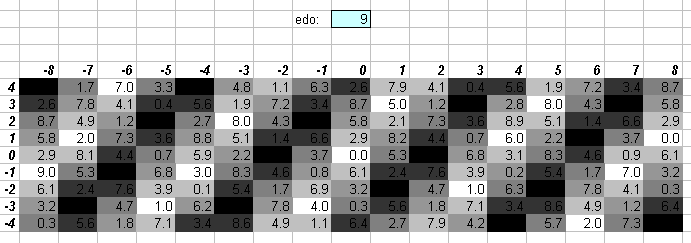
Note that 9edo is also available as a subset of 72edo. One degree of 9edo (133&1/3 cents) is nearly the same as 27:25 = [2 3 5]^[0 3 -2] (= ~133.2375749 cents).
10edo
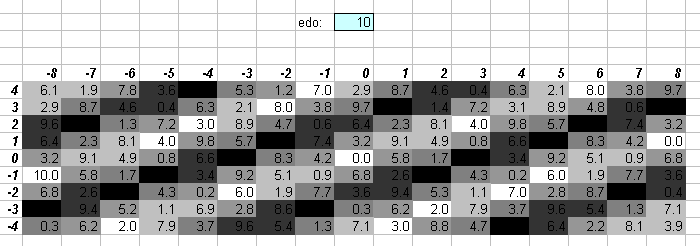
11edo
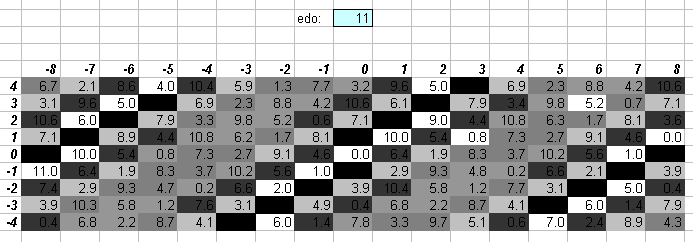
11edo and 13edo sound about as far away from 5-limit JI as any low-cardinality EDO can get. One degree of 11edo (~109.0909 cents) is fairly close to 16:15 = [2 3 5]^[4 -1 -1] (= ~111.7313 cents).
12edo
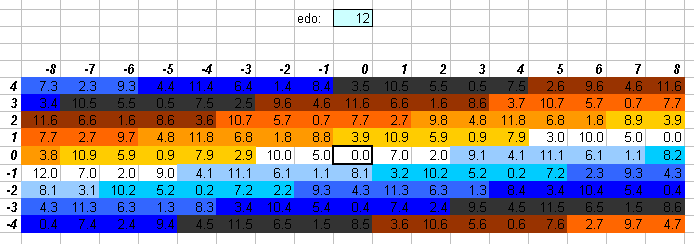
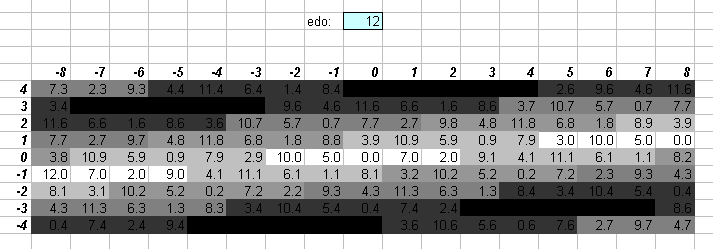
7 degrees of 12edo (exactly 700 cents) is very close to the Pythagorean "perfect 5th" with ratio 3:2 (= ~701.955 cents), and it can be seen immediately on the greyscale lattice that 12edo approximates Pythagorean (3-limit) quite well, and it is not too bad at approximating 5-limit either. 12edo is the smallest cardinality EDO which can represent the central section of the 5-limit lattice tolerably accurately, as well as the smallest EDO which can produce a recognizably diatonic scale (i.e., having two different-sized steps).
Because of this fair accuracy in the 5-limit,
12edo provides the simplest means of logarithmic interval measurement
where one wants to use only integers.
Some of the basic JI intervals are listed here
-- note that in many cases, several JI ratios are represented by
the same 12edo interval.
12edo prime interval
degrees vector ratio name
0 [ 8 1] 32805:32768 skhisma
0 [-4 -2] 2048:2025 diaschisma
0 [ 4 -1] 81:80 syntonic comma
0 [ 0 -3] 125:128 diesis
1 [-1 2] 25:24 JI chromatic semitone
1 [ 3 1] 135:128 Ellis larger limma, Rameau mean semitone
1 [-5 0] 256:243 limma
1 [-1 -1] 16:15 JI diatonic semitone
1 [ 3 -2] 27:25
2 [-2 1] 10:9 minor tone
2 [ 2 0] 9:8 major tone
2 [-2 -2] 256:225
3 [ 1 -1] 6:5 minor 3rd
4 [ 0 1] 5:4 major 3rd
5 [-1 0] 4:3 4th
7 [ 1 0] 3:2 5th
12edo can act simultaneously as 1/11-comma meantone, aristoxenean, schismic, diaschismic, and diesic, and diminished (octatonic), belonging to all of these families of temperaments -- and still others as well (as displayed on the diagram at the top of this page). This helps to explain its broad utility and appeal as a standard tuning.
Paul Erlich comments:
"12edo is [also] diminished/octatonic. this fact is even more important -- it's very important in the music of Mussorgsky, Rimsky-Korsakov, Stravinsky, Bartok, Lizst, Bloch, etc. . . -- and in a sense, romantic-era harmony can be best thought of as the intersection of meantone and diminished approaches -- hence unambiguously implying 12edo."
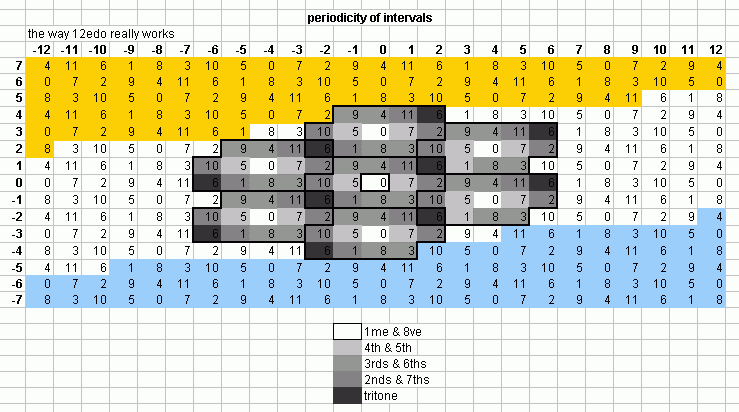
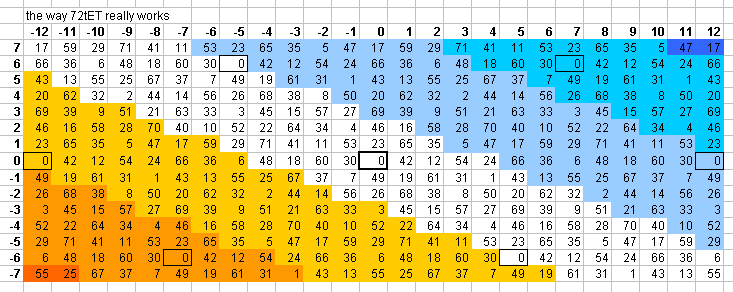
These 5-limit "vanishing commas" in 12edo can be seen on this "bingo-card" lattice:
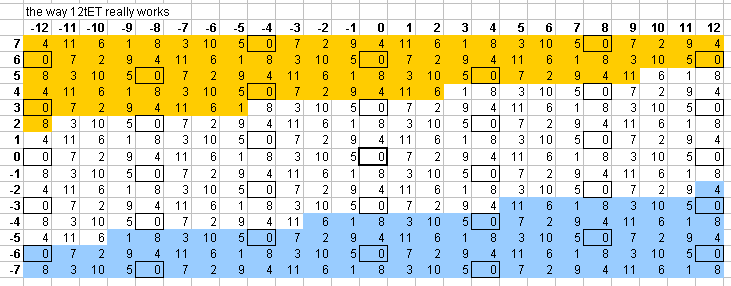
Here, the point where a 12edo degree is different from the nearest 12edo approximation of the corresponding ratio in the just lattice, is colored yellow where the 12edo note is 1 degree too high, and blue where it is 1 degree too low. The cells shaded in grey or outlined by a black line are all the instances of 2(0/12), which shows immediately which of the commas vanish, as per the graph given above.
Below is the same lattice, this time showing the periodicity
of intervals in 12edo by using grey shading according to the
legend at the bottom: unison and octave are white, the
perfect 4th and perfect 5th are the lightest grey, the major
and minor 3rds and 6ths are the next darker shade, the
major and minor 2nds and 7ths are the next darker, and
the tritone is the darkest.
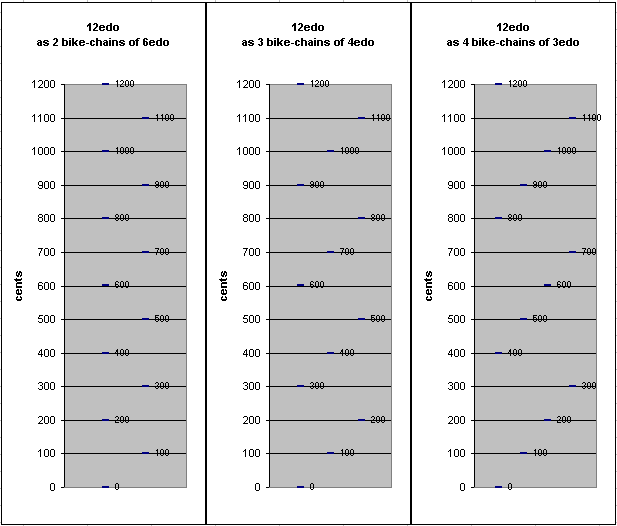
Because of its easy divisibility, 12edo can also be thought of as 2 bike-chains of 6edo (i.e., 2 distinct "whole-tone" scales) separated by a semitone; as 3 bike-chains of 4edo (i.e., 3 distinct "diminished-7th" tetrads) each separated by a semitone; and as 4 bike-chains of 3edo (i.e., 4 distinct "augmented" triads) each separated by a semitone.
Now, regarding 12edo's representation of higher primes ...
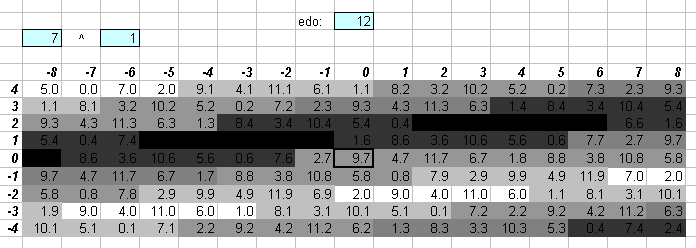
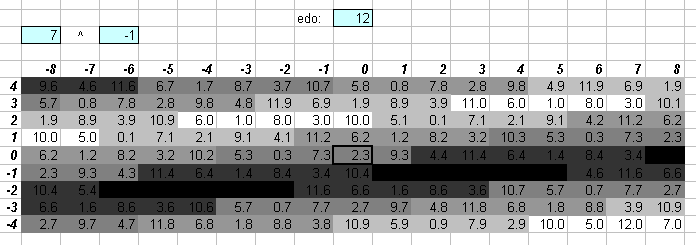
The two greyscale lattices above show that while 12edo is not very good at approximating prime-factor 7, the approximations are still close enough that in a particular musical context it is possible to imply 7 to some extent.
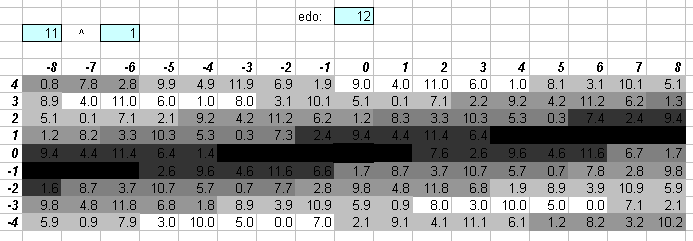

The two greyscale lattices above show that 12edo cannot approximate prime-factor 11 well enough to imply it. The basic 11-limit ratios, 11:8 and 16:11, are both shown as black squares here (at the [3 5]^[0 0] coordinates), indicating that those ratios fall right between two different 12edo degrees.
13edo
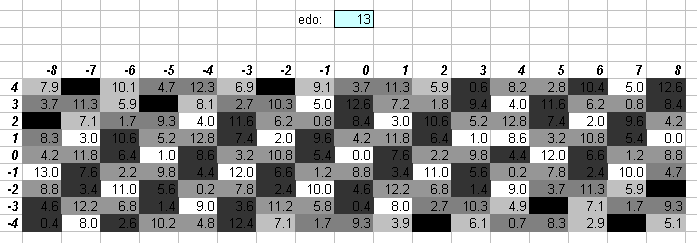
13edo and 11edo sound about as far away from 5-limit JI as any low-cardinality EDO can get. One degree of 13edo (~92.30769 cents) is quite close to 256:243 =[2 3 5]^[8 -5 0], the Pythagorean diatonic semitone or limma (= ~90.225 cents).
15edo
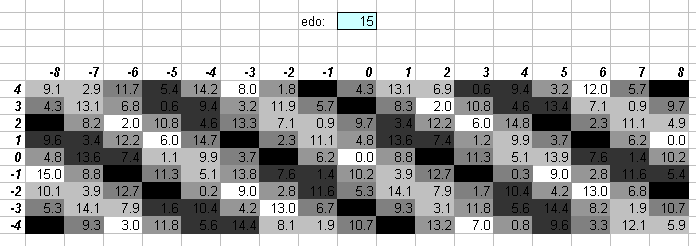
16edo
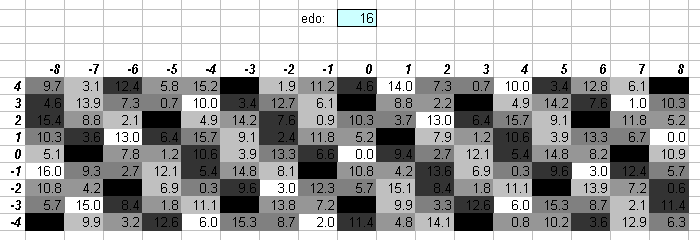
17edo
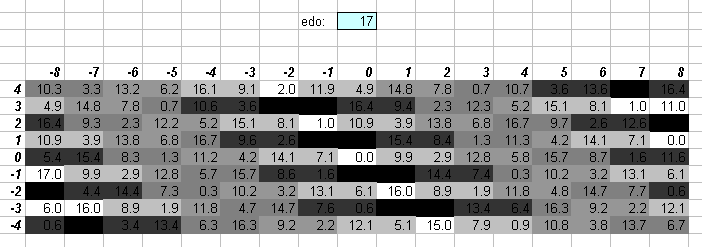
17edo is a quasi-Pythagorean tuning. The lattice clearly shows the horizontal orientation typical of a 3-limit system. One degree of 17edo (~70.58824 cents) is nearly identical to 25:24 = [2 3 5]^[-3 -1 2] (= ~70.67243 cents).
19edo

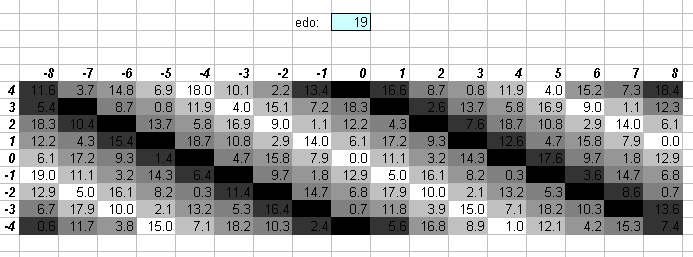
One degree of 19edo (~63.15789 cents) is quite close to 648:625 = [2 3 5]^[3 4 -4] (= ~62.56515 cents). The 19edo error from 5-limit JI follows the same kind of trend on my lattices as 1/3-comma meantone, with which it is audibly nearly identical (compare with this graph). The just "minor 3rds" and "major 6ths" are given nearly exactly. See also 152edo.
The 5-limit "vanishing commas" in 19edo can be seen on this "bingo-card" lattice:
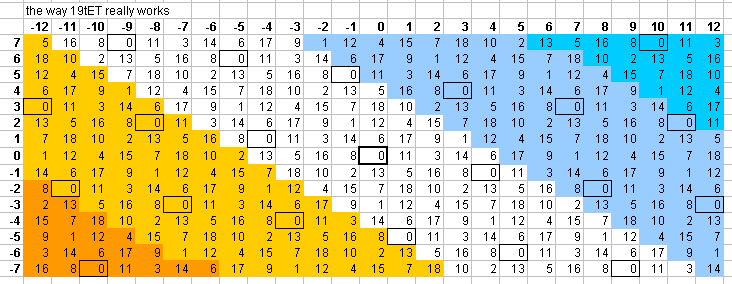
The pattern of accuracy in the 5-limit for
19edo provides a convenient means of logarithmic interval measurement
where one wants to use only integers
but wants more accuracy than 12edo.
Some of the basic JI intervals are listed here:
19edo prime interval
degrees vector ratio name
-1 [ 8 1] 32805:32768 skhisma
1 [-4 -2] 2048:2025 diaschisma
0 [ 4 -1] 81:80 syntonic comma
1 [ 0 -3] 125:128 diesis
1 [-1 2] 25:24 JI chromatic semitone
2 [-1 -1] 16:15 JI diatonic semitone
2 [ 3 -2] 27:25
3 [-2 1] 10:9 minor tone
3 [ 2 0] 9:8 major tone
5 [ 1 -1] 6:5 minor 3rd
6 [ 0 1] 5:4 major 3rd
8 [-1 0] 4:3 4th
11 [ 1 0] 3:2 5th
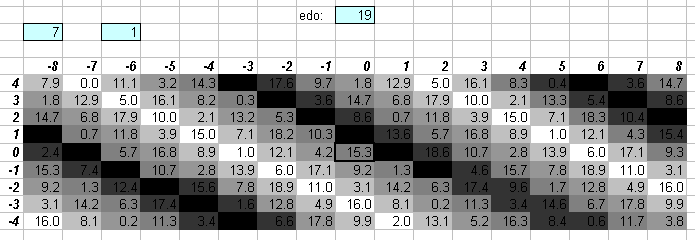
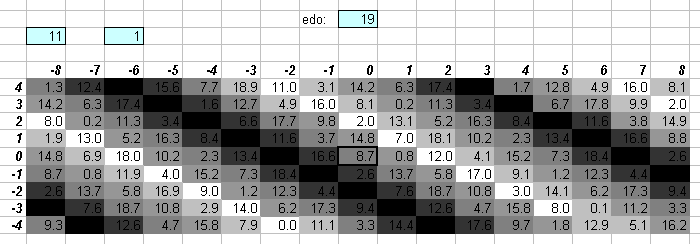
The two lattices above show that 19edo is about as good as 12edo at approximating prime-factor 7, and a good deal better at approximating 11. The "septimal 3rd" with ratio 7/6 is represented by 4 degrees of 19edo, the "harmonic 7th" with ratio of 7/4 by 15 degrees, and the ratio 11/8 by 9 degrees.
20edo
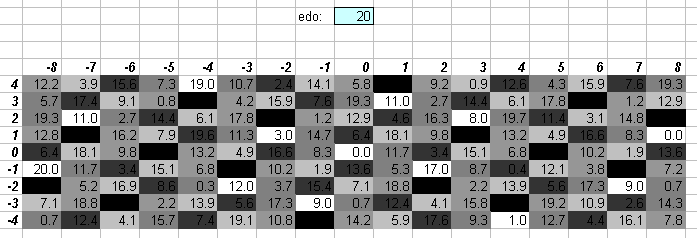
One degree of 20edo (exactly 60 cents) is also fairly close to 648:625 = [2 3 5]^[3 4 -4] (= ~62.56515 cents).
22edo
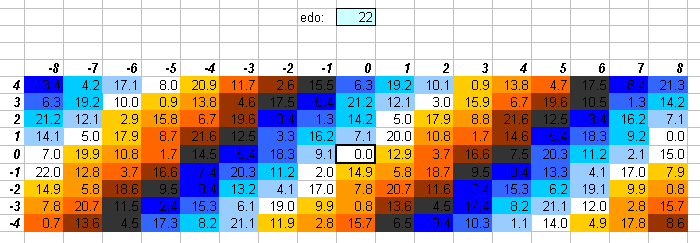
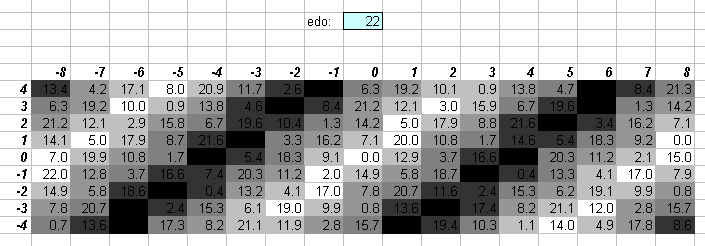
The 5-limit "vanishing commas" in 22edo can be seen on this "bingo-card" lattice:
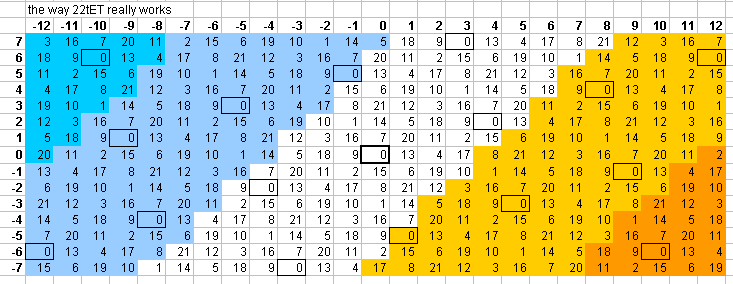
Paul Erlich has recommended 22edo as a new tuning because it gives reasonably good approximations of the higher prime-factors 7 and 11.
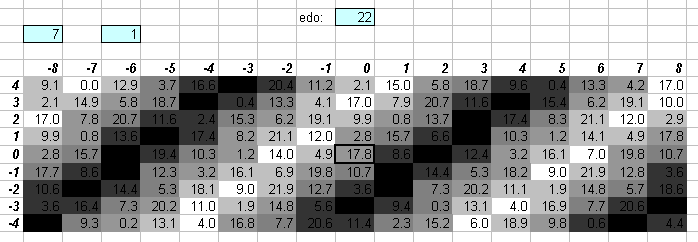
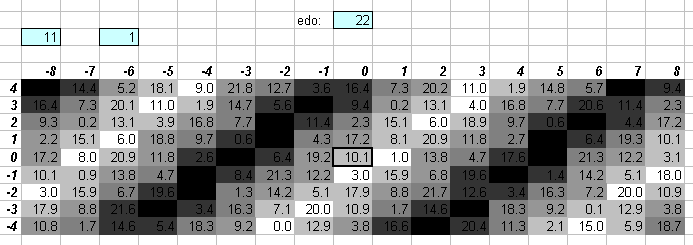
The two lattices above show that, compared to 12edo, 22edo gives a slightly better approximation of 7, and a much better approximation of 11.
23edo
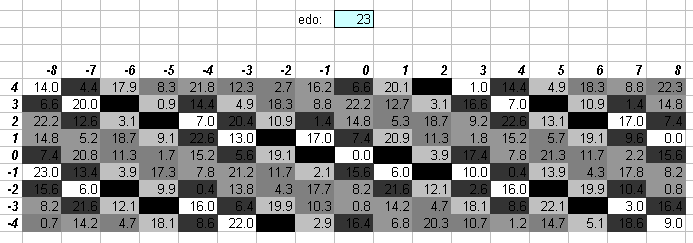
23edo probably has the least to do with 5-limit tuning than any other EDO near its cardinality size. One degree of 23edo is quite close to 16875:16384 = [2 3 5]^[-14 3 5] (= ~51.11986 cents).
24edo
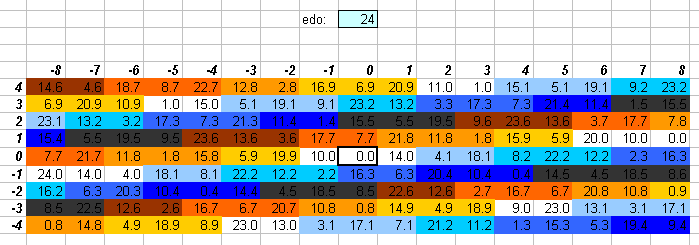
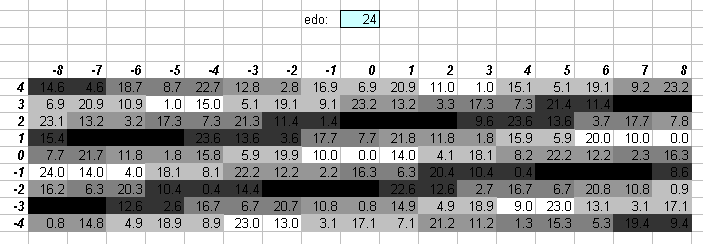
24edo is the system of 1/4-tones. It may be thought of as 2 separate bike-chains of 12edo, each separated by a 1/4-tone.
One degree of 24edo is quite close to 250:243 = [2 3 5]^[1 -5 3] (= ~49.16614 cents).

While 24edo gives an approximation of 7 which is better than that of 12edo, it is inconsistent with the approximation given by the sum of 24edo representations of 7-limit intervals: the best 24edo representation of the JI "major 3rd" (ratio 5:4) is 8 degrees of 24edo (= 400 cents), and the best representation of the 7:5 version of the tritone is 12 degrees of 24edo (= 600 cents). In JI, these two intervals add up to a 7:4 ratio, but the best 24edo approximation to the ("8ve"-reduced) 7th harmonic is 19 degrees, and the sum of the two best 24edo approximations to 5:4 and 7:5 is 8 + 12 = 20 degrees.

The lattice above shows that 24edo gives excellent approximations of prime-factor 11. Thus, if 7 is excluded, 24edo may be used to represent a [3 5 11] 11-limit JI tuning.
29edo
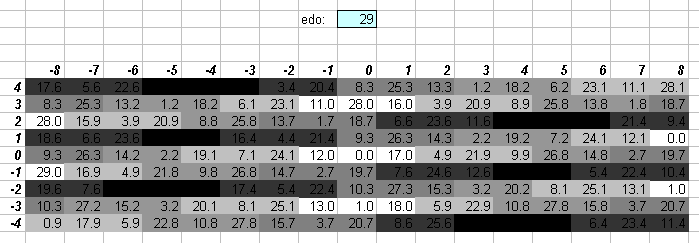
29edo is a variety of Pythagorean tuning and may also function as a schismic temperament.
31edo
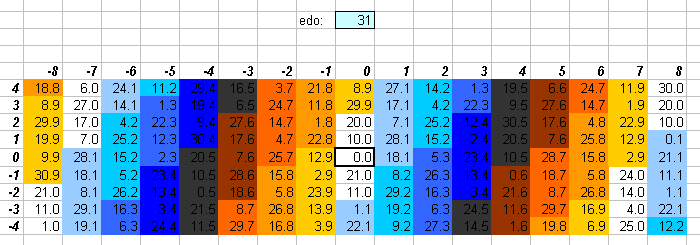
31edo is quite close to 1/4-comma meantone, and nearly exactly 7/29-comma and 13/54-comma meantone. It is easy to see that this lattice is much more vertically-oriented than any of the others so far (except for 3edo and 6edo, which are not large enough to create recognizable diatonicity), which shows that 31edo is very good at approximating prime-factor 5 (compare with this graph). When the term "1/5-tone" is used in tuning literature, it generally refers to one degree not of 30edo but of 31edo.
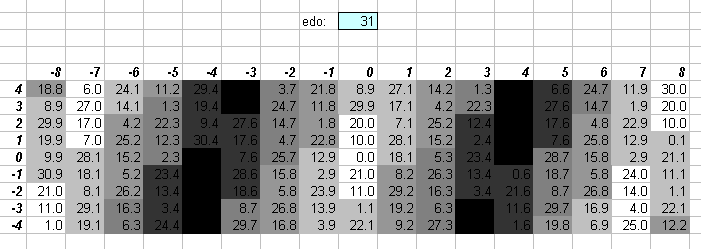
The lattice above shows that 31edo gives a superb rendering of 7-limit harmony. Assuming 1/4-comma meantone or its equivalent 31edo as the tuning, music of the Renaissance, Baroque, and Classical and Romantic periods often suggests 7-limit intervals, with 7:4 generally notated as the "augmented 6th" interval, the 4:5:7 triad as the "Italian 6th" chord, and the 4:5:6:7 tetrad as the "German 6th" chord.
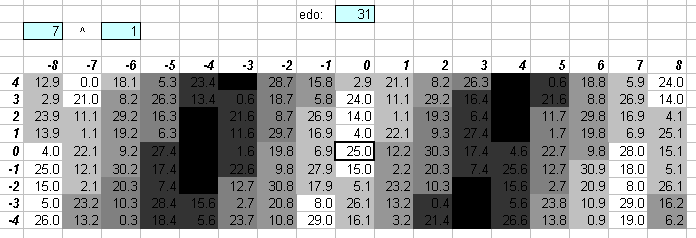
The lattice above shows that 31edo also gives a fairly decent approximation of prime-factor 11.
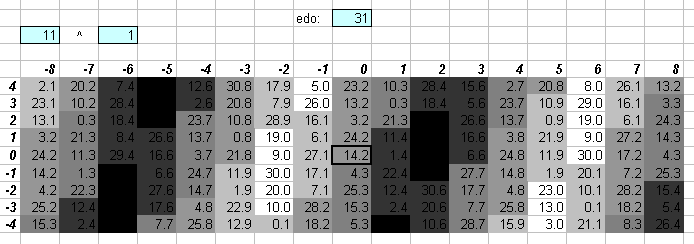
The 5-limit "vanishing commas" in 31edo can be seen on this "bingo-card" lattice:
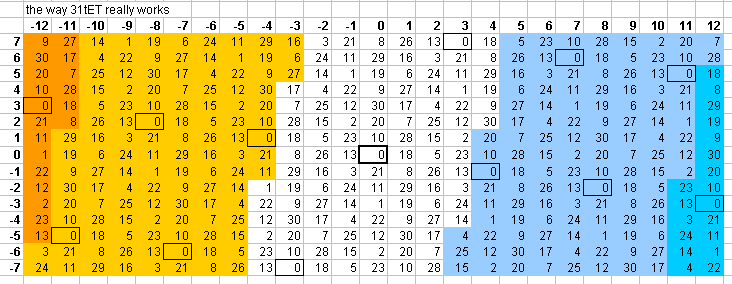
Some of the basic JI intervals are listed here
with their 31edo representations:
31edo prime interval
degrees vector ratio name
3 5
-1 [ 8 1] 32805:32768 skhisma
1 [-4 -2] 2048:2025 diaschisma
0 [ 4 -1] 81:80 syntonic comma
1 [ 0 -3] 128:125 diesis
2 [-1 2] 25:24 JI chromatic semitone
2 [ 3 1] 135:128 Ellis larger limma, Rameau mean semitone
3 [-5 0] 256:243 limma
3 [-1 -1] 16:15 JI diatonic semitone
3 [ 3 -2] 27:25
5 [-2 1] 10:9 minor tone
5 [ 2 0] 9:8 major tone
6 [-2 -2] 256:225
8 [ 1 -1] 6:5 minor 3rd
10 [ 0 1] 5:4 major 3rd
13 [-1 0] 4:3 4th
18 [ 1 0] 3:2 5th
The "septimal 3rd" with ratio 7/6 is represented by 7 degrees of 31edo, the "harmonic 7th" with ratio of 7/4 by 25 degrees, and the ratio 11/8 by 14 degrees.
33edo

33edo is at the bottom limit of meantone-like systems, because its "whole-tone" (5 degrees of 33edo = ~181.8182 cents) is very close to the 10:9 ratio (= ~182.4037 cents), which means that it is tempered a full syntonic comma lower than the Pythagorean "whole-tone" 9:8, thus leaving no more room for a "mean" tone between the two different just versions. 33edo is equivalent to 1/2-comma meantone.
34edo
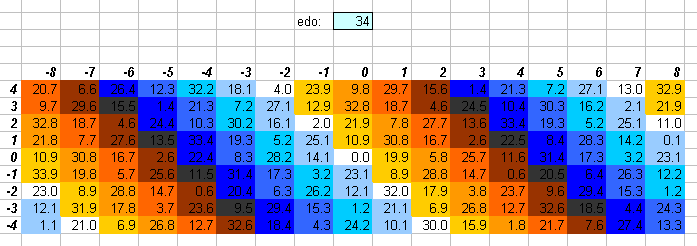
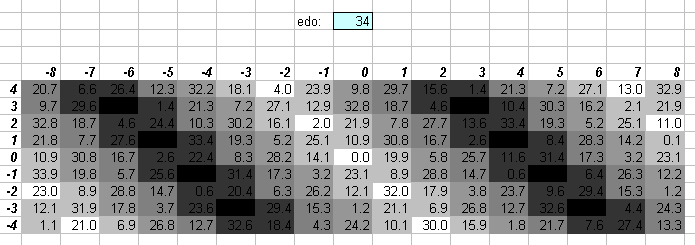
34edo is a positive system which gives good 5-limit approximations.
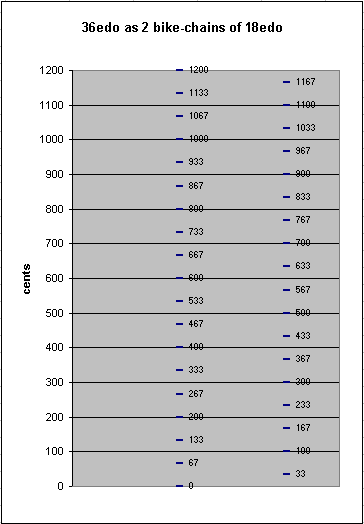
36edo
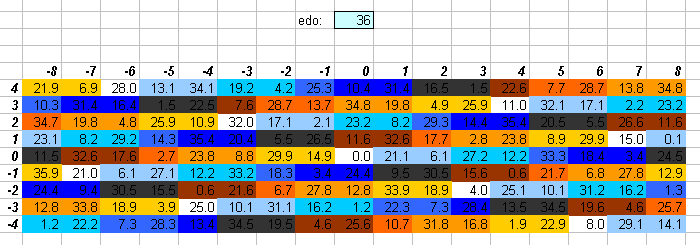
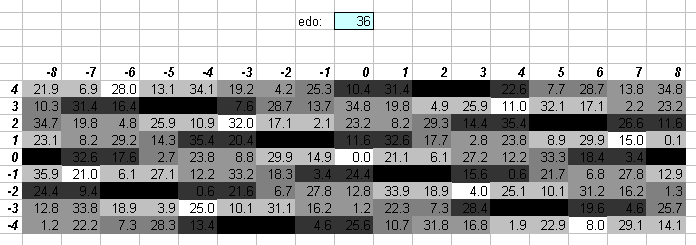
36edo is the system of 1/6-tones. It may be thought of as 3 separate bike-chains of 12edo, each separated by a 1/6-tone.

36edo was advocated by Busoni in 1906 in his Sketch of a New Aesthetic of Music, not with the intention of obtaining better approximations of 5-limit tuning (which the lattice shows it does not do well), but rather with the express intention of expanding the composer's palette of pitch resources. Busoni's conception of 36edo was as 2 bike-chains of 18edo, each separated by a semitone. This made his idea for notating it a bit unweildy -- it would have been better to think of the chains as being separated by a 1/6-tone.
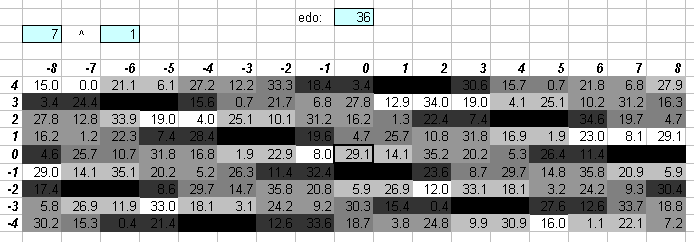
36edo gives a good approximation of prime-factor 7,and is also consistent in the 7-limit.

The lattice above shows that 36edo does not really offer an improvement in approximating prime-factor 11, since the 11:8 ratio (represented by the black square at the [3 5]^[0 0] coordinate above) falls directly between two different 36edo degrees.
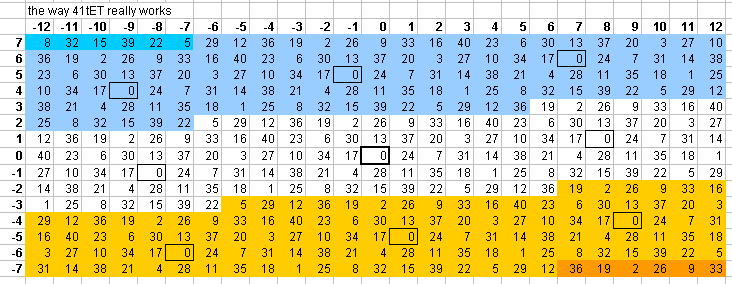
41edo
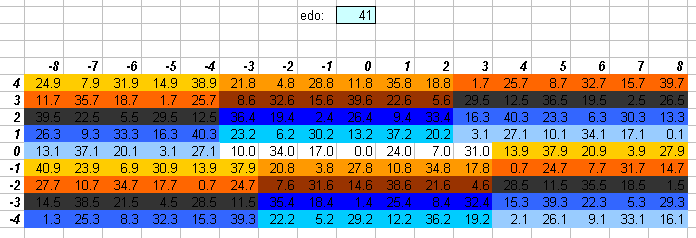

41edo provides an excellent approximation to Pythagorean tuning: 24 degrees of 41edo (~702.439 cents) is quite close to the Pythagorean "perfect 5th" 3:2 = [2 3 5]^[-1 1 0] (~701.955 cents). The lattice shows that the error is no more than 1/10 of a 41edo degree for the entire Pythagorean axis 3(-8...8) on this diagram. 41edo is also good enough at approximating the most basic 5-limit ratios that it has some utility in representing 5-limit tuning as well, and it may also function as a schismic temperament.
The 5-limit "vanishing commas" in 41edo can be seen on this "bingo-card" lattice:
41edo is also quite good in both the 7-limit and (just a bit less so) 11-limit:
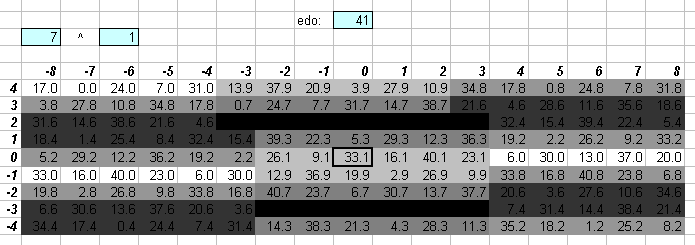
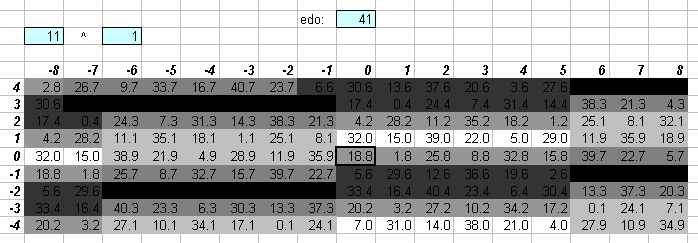
43edo
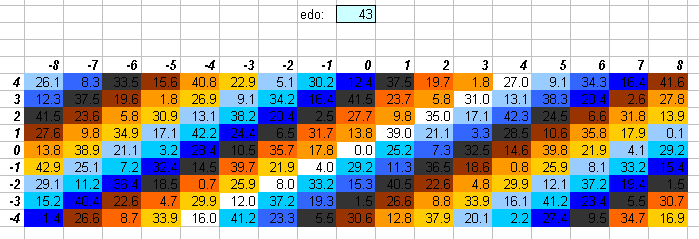
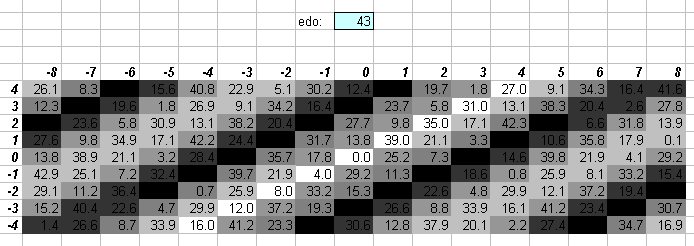
43edo is nearly identical to 1/5-comma meantone (compare with this graph). One degree of 43edo is the unit of interval measurement called a meride, used by Joseph Saveur. 43edo is related to 301edo.
46edo
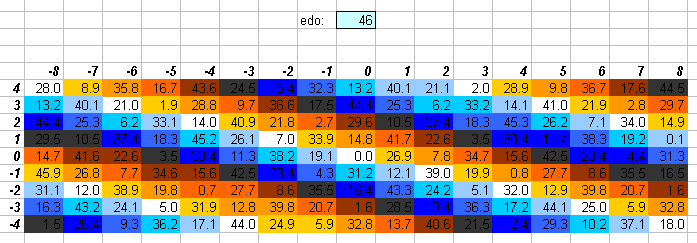
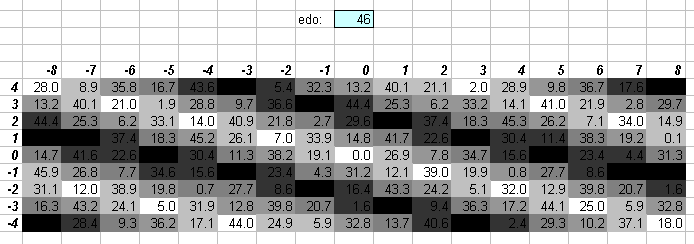
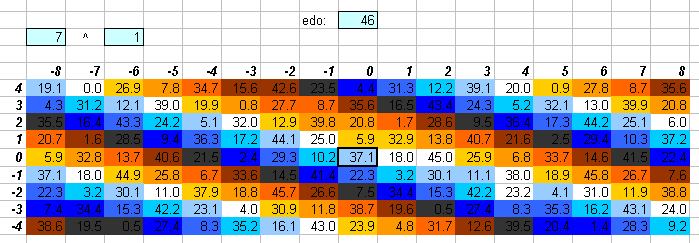

These lattices show that 46edo gives an excellent approximation to all the basic intervals ("5th", "major-3rd", "minor-3rd", "harmonic-7th", "harmonic-11th") in the 11-limit.
48edo

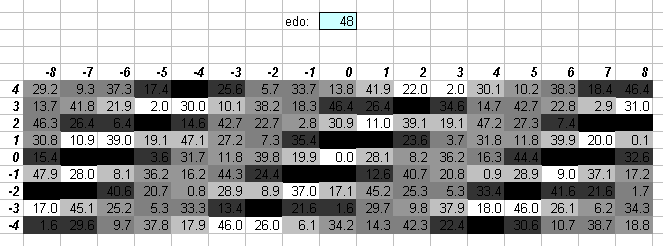
48edo is the system of 1/8-tones. It may be thought of as 4 separate bike-chains of 12edo, each separated by a 1/8-tone.
50edo
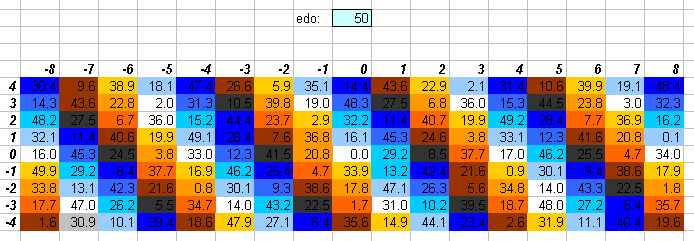
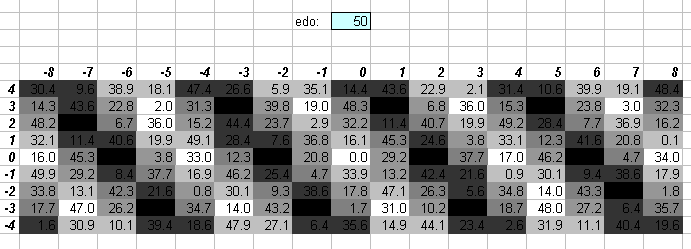
50edo is also a negative system, and it approximates both Zarlino's 2/7-comma and Woolhouse's 7/26-comma meantone well (compare with this graph).
53edo
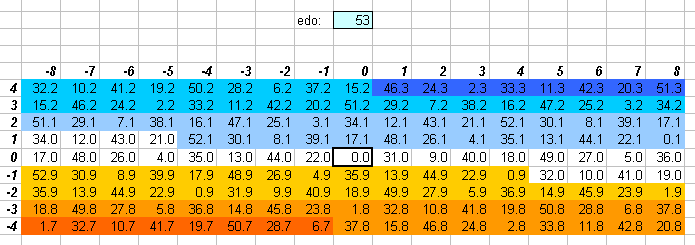
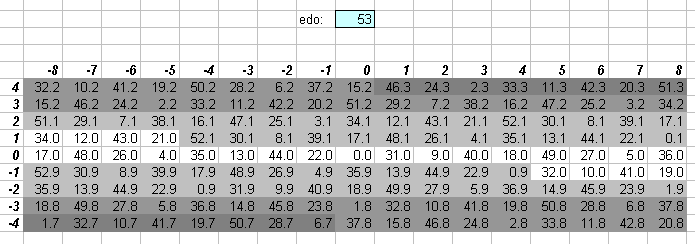
It can be seen that the error of 53edo on this lattice is nowhere very great, thus, 53edo is a superb approximation to the entire central section of the 5-limit lattice. In addition, note that the error along the entire Pythagorean axis 3(-8...8) is zero, thus 53edo is also the lowest cardinality EDO which is essentially identical to a long enough section of the Pythagorean lattice (chain) to include the Pythagorean comma (~23.46001 cents, which is in fact almost the same as one degree of 53edo = ~22.64151 cents), and is the next closer approximation to Pythagorean after 41edo. In addition to being nearly identical to both Pythagorean and just-intonation tunings, 55edo may also function as a schismic or kleismic temperament.
Because of this accuracy in the 5-limit,
53edo provides a convenient means of logarithmic interval measurement
where one wants to use only integers.
Some of the basic JI intervals are listed here:
53edo prime interval
degrees vector ratio name
3 5
0 [ 8 1] 32805:32768 skhisma
1 [-4 -2] 2048:2025 diaschisma
1 [ 4 -1] 81:80 syntonic comma
2 [ 0 -3] 128:125 diesis
3 [-1 2] 25:24 JI chromatic semitone
4 [ 3 1] 135:128 Ellis larger limma, Rameau mean semitone
4 [-5 0] 256:243 limma
5 [-1 -1] 16:15 JI diatonic semitone
6 [ 3 -2] 27:25
8 [-2 1] 10:9 minor tone
9 [ 2 0] 9:8 major tone
10 [-2 -2] 256:225
14 [ 1 -1] 6:5 minor 3rd
17 [ 0 1] 5:4 major 3rd
22 [-1 0] 4:3 4th
31 [ 1 0] 3:2 5th
Larger EDOs which offer increasing accuracy in the 5-limit, and thus make better interval measurements, are 65edo, 118edo, 612edo, 730edo, and 4296edo.
55edo
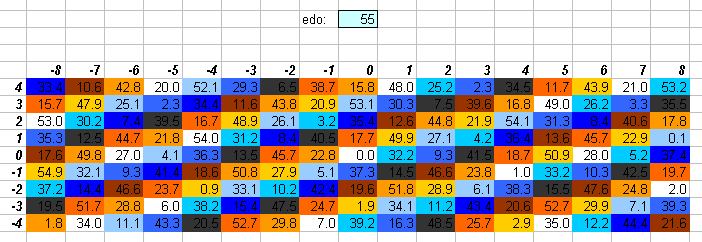
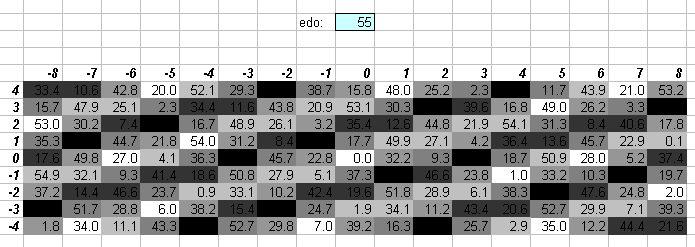
55edo is close to 1/6-comma meantone, and nearly identical to 3/17-comma meantone (compare with this graph). Note that one degree of 55edo (= ~219/11 cents), is nearly the same as the syntonic comma (= ~211/2 cents).
See my webpage on 55edo.
58edo
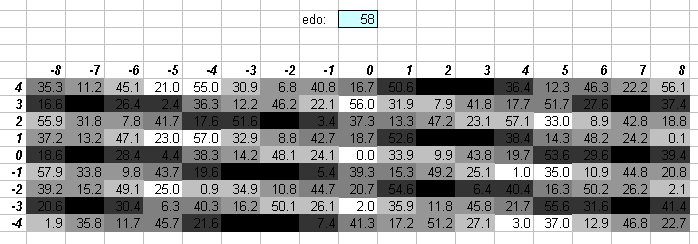
58edo can be thought of as 2 bike-chains of 29edo.
65edo
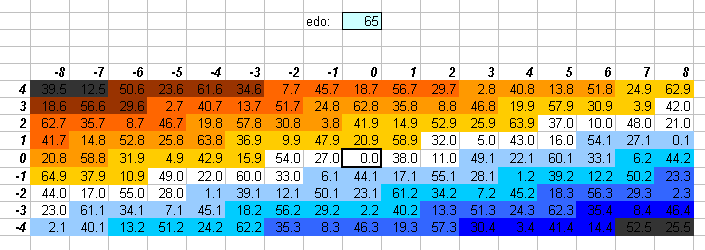
65edo provides an excellent approximation to the 5-limit lattice.
Because of this accuracy in the 5-limit,
65edo provides a excellent means of logarithmic interval measurement
where one wants to use only integers.
Some of the basic JI intervals are listed here:
65edo prime interval
degrees vector ratio name
3 5
0 [ 8 1] 32805:32768 skhisma
1 [-4 -2] 2048:2025 diaschisma
1 [ 4 -1] 81:80 syntonic comma
2 [ 0 -3] 128:125 diesis
4 [-1 2] 25:24 JI chromatic semitone
5 [ 3 1] 135:128 Ellis larger limma, Rameau mean semitone
5 [-5 0] 256:243 limma
6 [-1 -1] 16:15 JI diatonic semitone
7 [ 3 -2] 27:25
10 [-2 1] 10:9 minor tone
11 [ 2 0] 9:8 major tone
17 [-2 -2] 256:225
17 [ 1 -1] 6:5 minor 3rd
21 [ 0 1] 5:4 major 3rd
27 [-1 0] 4:3 4th
38 [ 1 0] 3:2 5th
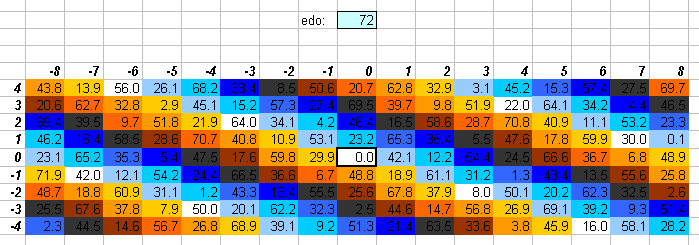
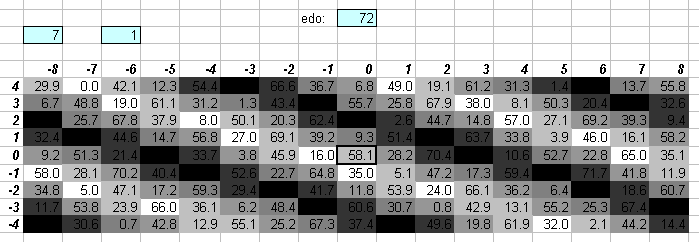
72edo
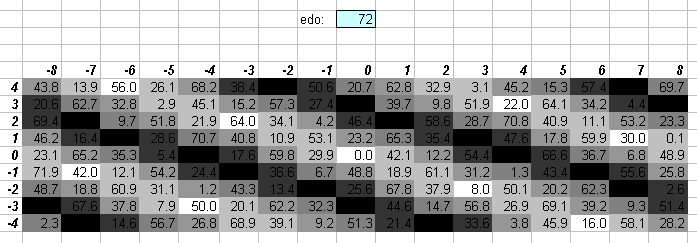
The 5-limit "vanishing commas" in 72edo can be seen on this "bingo-card" lattice:
Because of its acceptance by many microtonalists around 2000 as a
tuning and/or notation standard, 72edo is one of the more
important of the tunings described on this page.
Some of the basic JI intervals are listed here:
72edo prime interval
degrees vector ratio name
3 5
-1 [ 8 1] 32805:32768 skhisma
2 [-4 -2] 2048:2025 diaschisma
1 [ 4 -1] 81:80 syntonic comma
3 [ 0 -3] 128:125 diesis
4 [-1 2] 25:24 JI chromatic semitone
5 [ 3 1] 135:128 Ellis larger limma, Rameau mean semitone
6 [-5 0] 256:243 limma
7 [-1 -1] 16:15 JI diatonic semitone
8 [ 3 -2] 27:25
11 [-2 1] 10:9 minor tone
12 [ 2 0] 9:8 major tone
14 [-2 -2] 256:225
19 [ 1 -1] 6:5 minor 3rd
23 [ 0 1] 5:4 major 3rd
30 [-1 0] 4:3 4th
42 [ 1 0] 3:2 5th
Scales which have cardinalities which are multiples of 12 (24, 36, 48) have often been recommended as a means of expanding the composer's pitch resources. 72edo is the first scale which is a multiple of 12edo, to offer a better approximation of prime-factor 5 than 12edo. 72edo may be thought of as 6 separate bike-chains of 12edo, each separated by a 1/12-tone.
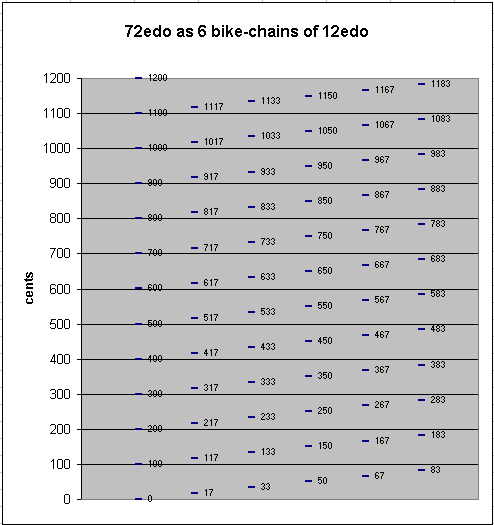
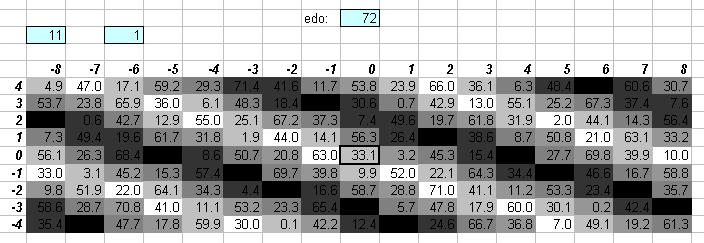
The two lattices above show the good approximations to 7- and 11-limit ratios given by 72edo, and that it is about equally good at approximating all prime-factors within the 11-limit.
84edo
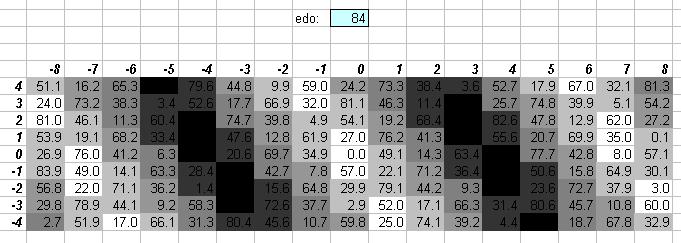
94edo
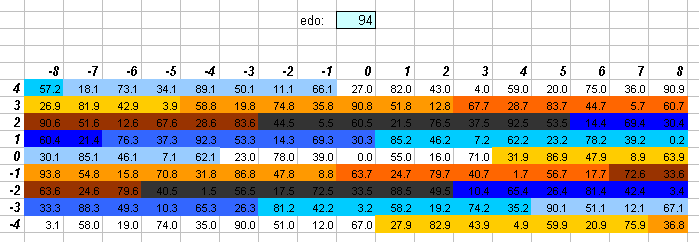
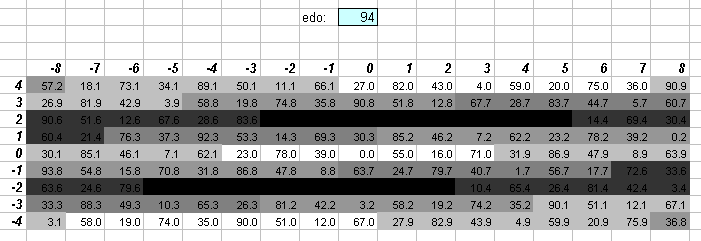
111edo
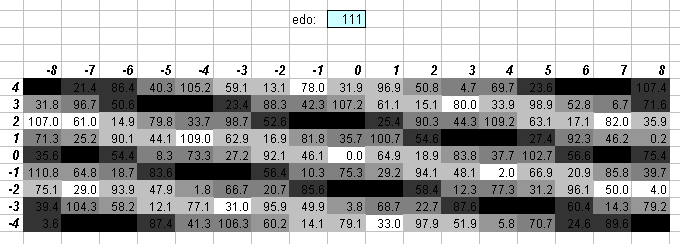
118edo
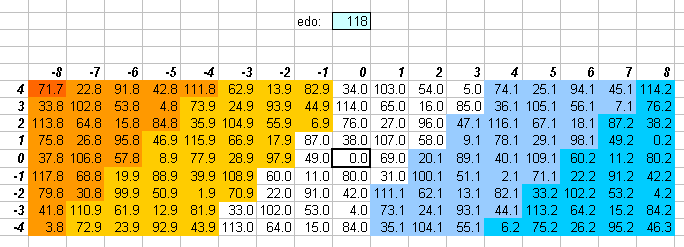
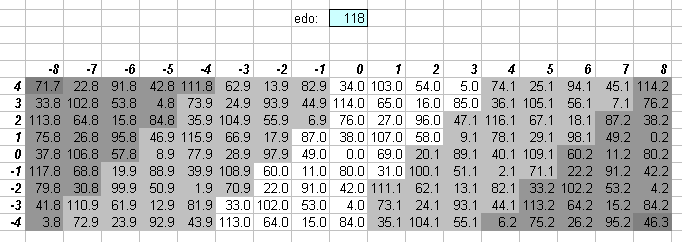
The lattice shows clearly that 118edo gives an outstanding approximation to 5-limit JI. The entire central core is given with practically no error. This makes 118edo quite good as an interger interval measurement for the 5-limit.
Because of this accuracy in the 5-limit,
118edo provides a excellent means of logarithmic interval measurement
where one wants to use only integers.
Some of the basic JI intervals are listed here:
118edo prime interval
degrees vector ratio name
3 5
0 [ 8 1] 32805:32768 skhisma
2 [-4 -2] 2048:2025 diaschisma
2 [ 4 -1] 81:80 syntonic comma
4 [ 0 -3] 128:125 diesis
7 [-1 2] 25:24 JI chromatic semitone
9 [ 3 1] 135:128 Ellis larger limma, Rameau mean semitone
9 [-5 0] 256:243 limma
11 [-1 -1] 16:15 JI diatonic semitone
13 [ 3 -2] 27:25
18 [-2 1] 10:9 minor tone
20 [ 2 0] 9:8 major tone
22 [-2 -2] 256:225
31 [ 1 -1] 6:5 minor 3rd
38 [ 0 1] 5:4 major 3rd
49 [-1 0] 4:3 4th
69 [ 1 0] 3:2 5th
118edo vector
degree cents 3 5 name
0 0 [ 0 0] prime
[-2 -15] ?
[ 8 1] skhisma
[ 6 -14] ?
1 10 10/59 [-5 6] kleisma
[ 3 7] semicomma
[ 1 -8] Wurschmidt's comma
2 20 20/59 [-4 -2] diaschisma
[ 4 -1] syntonic comma
[12 0] Pythagorean comma
3 30 30/59 [-9 4] minimal diesis
[-1 5] small diesis (magic comma)
[ 7 6] ampersand's comma
4 40 40/59 [ 0 -3] diesis
[ 8 -2] superdiesis
5 50 50/59 [ 3 4]
[-5 3] porcupine
6 61 1/59 [-4 -5]
[ 4 -4] major diesis (diminished scale)
7 71 11/59 [-1 2] JI chromatic semitone
8 81 21/59 [ 0 -6]
9 91 31/59 [-5 0] Pythagorean limma
[ 3 1] JI larger limma
10 101 41/59 [-2 7]
11 111 51/59 [-1 -1] JI diatonic semitone
12 122 2/59 [ 2 6]
13 132 12/59 [ 3 -2] great limma
14 142 22/59 [-2 4]
15 152 32/59 [-1 -4]
16 162 42/59 [ 2 3]
17 172 52/59 [ 3 -5]
18 183 3/59 [-2 1] JI minor-tone
19 193 13/59 [-1 -7]
20 203 23/59 [ 2 0] Pythagorean major-tone
21 213 33/59 [-3 6]
22 223 43/59 [-2 -2] JI diminished-3rd
23 233 53/59 [ 1 5]
24 244 4/59 [ 2 -3] acute diminished-3rd
25 254 14/59 [-3 3] grave augmented-2nd
26 264 24/59 [-2 -5]
27 274 34/59 [ 1 2] augmented-2nd
28 284 44/59 [ 2 -6]
29 294 54/59 [-3 0] Pythagorean minor-3rd (trihemitone)
30 305 5/59 [ 0 7]
31 315 15/59 [ 1 -1] JI minor-3rd
32 325 25/59 [-4 5]
33 335 35/59 [-3 -3]
34 345 45/59 [ 0 4]
35 355 55/59 [ 1 -4]
36 366 6/59 [-4 2]
37 376 16/59 [-3 -6]
38 386 26/59 [ 0 1] JI major-3rd
[-8 0] Pythagorean diminished-4th
39 396 36/59 [ 1 -7]
40 406 46/59 [ 4 0] Pythagorean major-3rd (ditone)
41 416 56/59 [-1 6]
42 427 7/59 [ 0 -2] JI diminished-4th
43 437 17/59 [ 3 5]
44 447 27/59 [ 4 -3]
45 457 37/59 [ 1 3] superfluous 3rd
46 467 47/59 [ 0 -5]
47 477 57/59 [ 3 2] grave 4th
48 488 8/59 [ 4 -6]
49 498 18/59 [-1 0] perfect-4th
50 508 28/59 [ 2 7]
51 518 38/59 [ 3 -1] acute 4th
52 528 48/59 [-2 5]
53 538 58/59 [-1 -3]
54 549 9/59 [ 2 4]
55 559 19/59 [ 3 -4]
56 569 29/59 [-2 2] superfluous 4th
57 579 39/59 [-1 -6]
58 589 49/59 [ 2 1] JI augmented-4th (tritone)
59 600 [-3 7]
[ 3 -7]
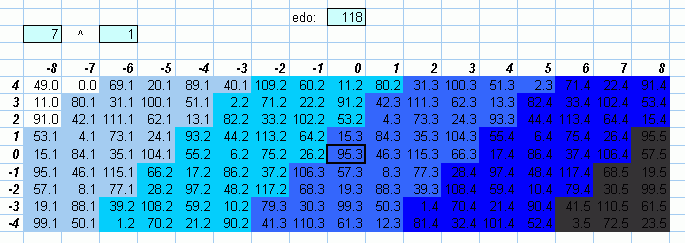
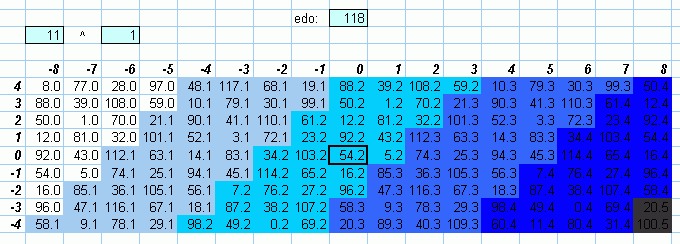
The above lattices show that 118edo, while still not bad, is not quite as good as an integer interval measurement for the 7- and 11-limit as it is for the 5-limit.
144edo
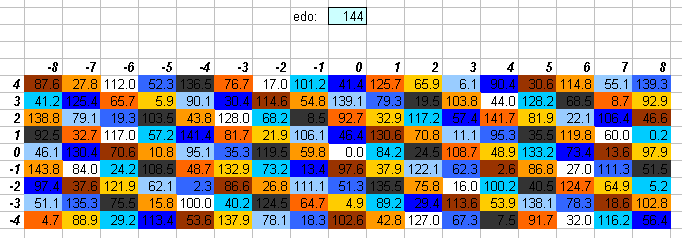
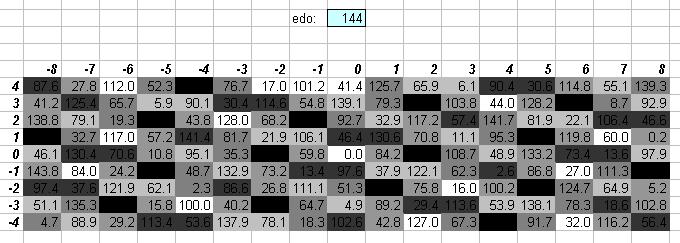
144edo was recommended for use by Joseph Schillinger, and more recently Dan Stearns and I have used it as a notation to represent very complex combinations of various tuning systems being used in the same piece, Stearns for the combinations of different EDOs, and myself for combinations of 12edo and extended JI (as in my piece A Noiseless Patient Spider). I stress here that neither of us use 144edo as a tuning, but merely as a notation; see the 144edo definition.
152edo
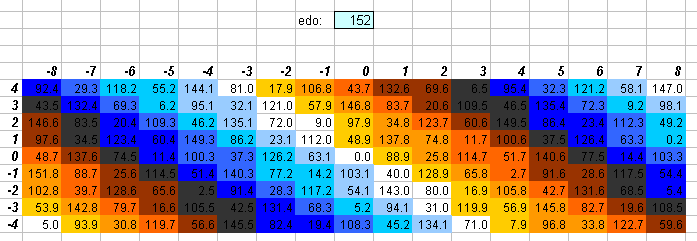
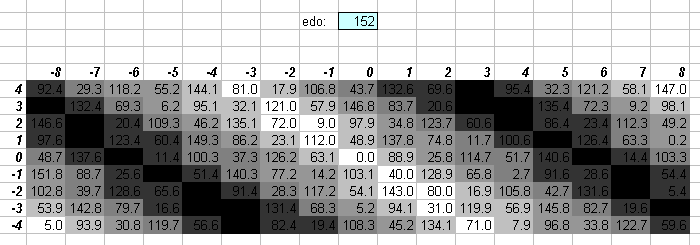
152 = 8 * 19, so 152edo may be thought of as 8 separate bike-chains of 19edo, each separated by a 3/76-tone (~7.894736842 cents).

Actually, the chains can be thought of as being approximately 1/3-comma (= ~7.168763199 cents) apart, so that 152 is a relatively concise fixed tuning that works as an adaptive JI. It also emulates such a wide variety of other tunings that Paul Erlich has proposed it as a "universal tuning":
personally, as i've mentioned before, if i were to choose a large ET for composing, it would be 152-equal (8*19) . . . in addition to supporting a 1/3-comma version of adaptive (5-limit) JI, it's really good through 11-limit strict JI. combine this with the fact that 76- equal (152/2) comes up as 'universally' important in my paper (near the end), and that 152 affords the opportunity to 'adaptively' realize the resources of 76-equal but with far better vertical harmony, and you get an idea of a few of the reasons i like 152.[from Yahoo tuning group message 36560, Mon Apr 22, 2002 5:11 pm]
171edo
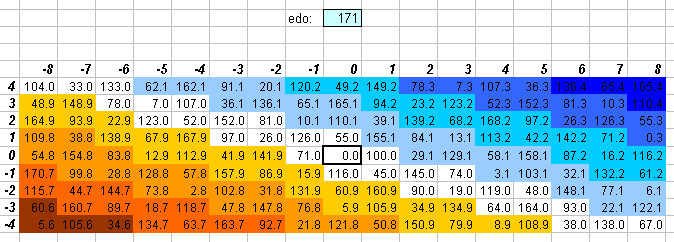
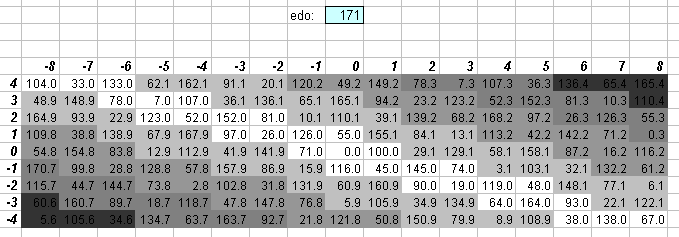
171edo was recommended by prolific German theorist Martin Vogel, who built a keyboard instrument in this tuning. It can be seen that, for such a large cardinality size, 171edo's approximations to 5-limit ratios, while quite good, do not surpass the accuracy of 118edo; but to be fair, Vogel chose 171edo because he intended to have close approximations to 7-limit ratios as well ...
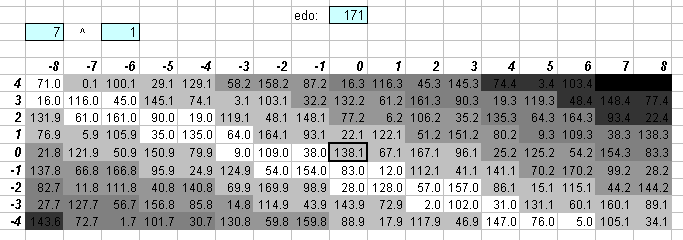
The lattice above shows that 171edo has excellent approximations to prime-factor 7 -- in fact, the pattern given by the amount of error is nearly identical to the 5-limit lattice above.
171edo may be thought of as 9 separate bike-chains of 19edo, each separated by a 2/57-tone.
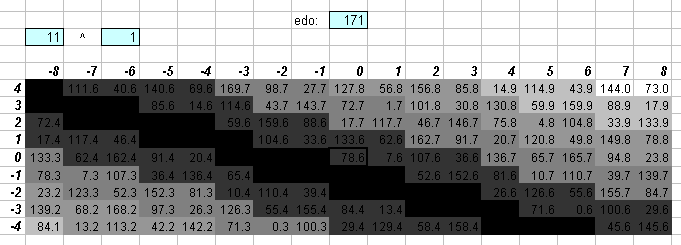
Curiously, however, as good as 171edo is at approximating 5 and 7, it is conversely just as bad at approximating 11.
183edo

183edo gives a very good approximation to the 5-limit lattice.
217edo


217edo received a lot of attention among tuning theorists in 2002, for its ability to represent a myriad of JI, adaptive-JI, and EDO tunings.
217edo may be thought of as 7 separate bike-chains of 31edo, each separated by a 6/217-tone.
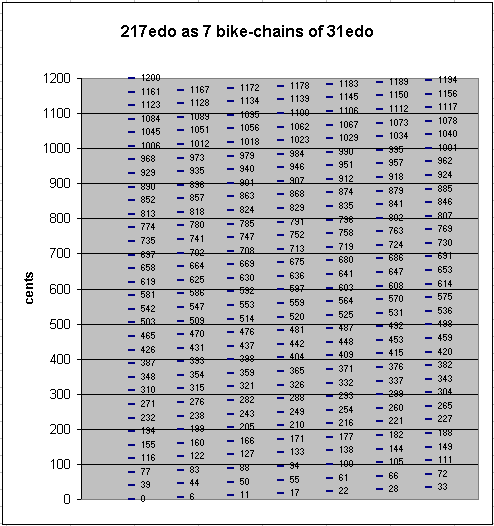
Embedded within it is a very close approximation to Vicentino's "second tuning" of 1555, which combined 1/4-comma meantone with Pythagorean "perfect 5ths".
301edo

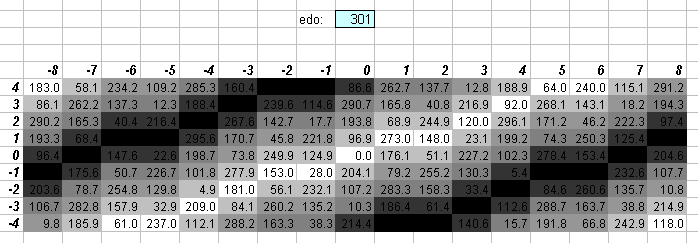
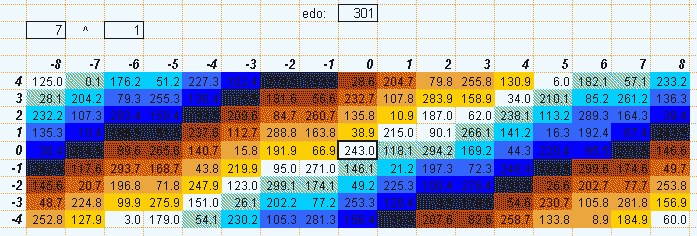
One degree of 301edo was used as a unit of interval measurement by Joseph Saveur and called a heptameride. 301 was chosen because it is a rounded multiple of log10(2) = ~0.301029996, thus obviating the need to calculate logarithms. It is related to Saveur's unit called meride, which is one degree of 43edo.
323edo
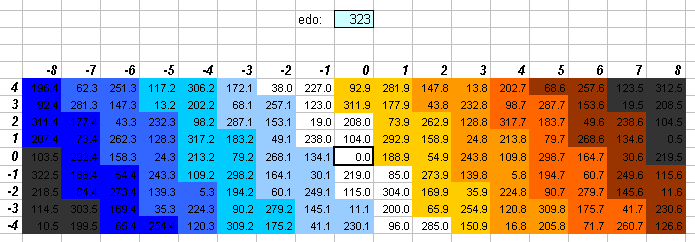
323edo is a tuning that has been used by Marc
Jones. Marc points out that it has four types of "5th" resembling
or identical to those of some other tunings:
17edo "5th" 2^(190/323) = 2^(10/17) = ~705.8823529 cents
near just "5th" 2^(189/323) = ~702.1671827 cents
near-12edo "5th" 2^(188/323) = ~698.4520124 cents
19edo "5th" 2^(187/323) = 2^(11/19) = ~694.7368421 cents
612edo
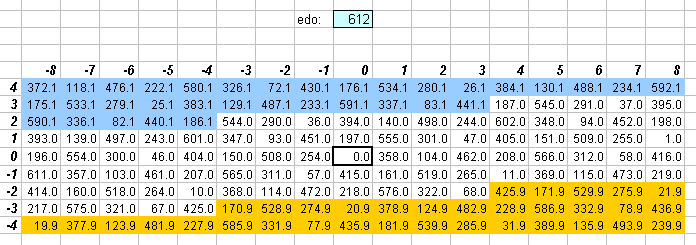
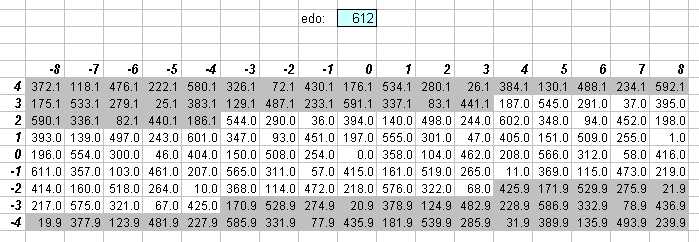
As this lattice shows, 612edo is nearly perfect for use as a 5-limit interval measurement where only integers are used, as there is practically no error for a large central section of the 5-limit lattice. 1 degree of 612edo is nearly identical in size to the skhisma.
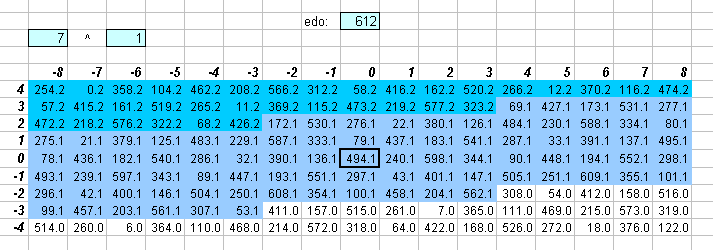
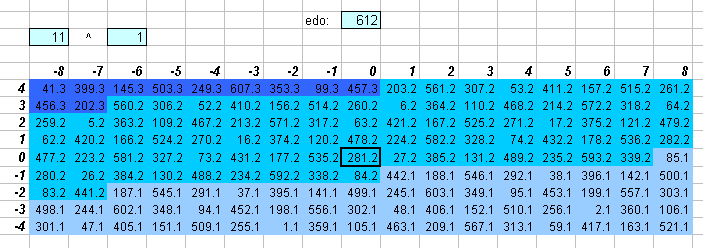
The two lattices above show that 612edo is quite good but not great as an integer interval measurement for 7- and 11-limit harmony.
730edo
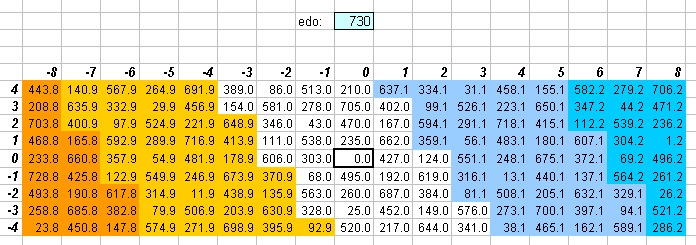
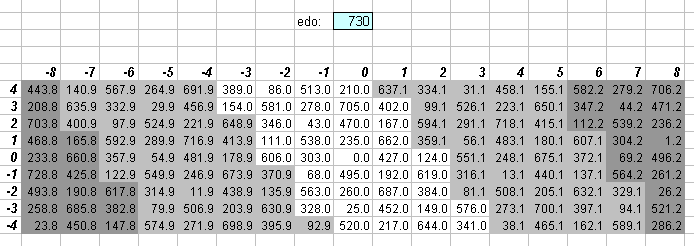
730edo is generated by the interval used as a measurement by Wesley Woolhouse because of its closeness of approximation to the central section of the 5-limit lattice, so that only integers need be employed.
Woolhouse's choice is interesting, because while he stated, in seeking an integer logarithmic interval measurement, that 730edo "differs less than any other from the true series [i.e., the just ratios], unless we ascend to very high numbers; and is the one which is therefore most to be recommended", it can be seen from these diagrams that 612edo actually gives better overall accuracy in the 5-limit. [Paul Erlich comments: "this is not the case. 612 gives better *relative* accuracy, but 730 gives better *absolute* accuracy, which is what woolhouse meant."]
But the pattern of zero error in 730edo resembles the general pattern of 50edo (and to a lesser extent, 19edo) -- which approximates his "optimal" 7/26-comma meantone -- whereas the pattern of 612edo does not. The conclusion this suggests to me is that Woolhouse chose 730edo over 612edo for this reason. The pitches he cared about most, which would follow the diagonal northwest-to-southeast trend of the 50edo lattice, would thus be given logarithmically as integers with excellent accuracy. [More from Paul: "i'm afraid you're stumbling on a mere coincidence -- the choice of 730-equal does not incorporate the major assumption behind his ultimate choice of 50-equal."]
768edo
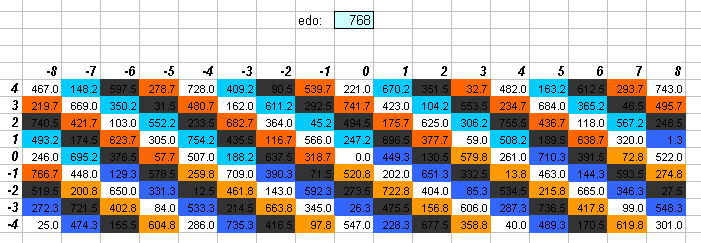
768edo is the tuning resolution on a variety of different electronic instruments, including the popular Yamaha TX-81Z.
1000edo
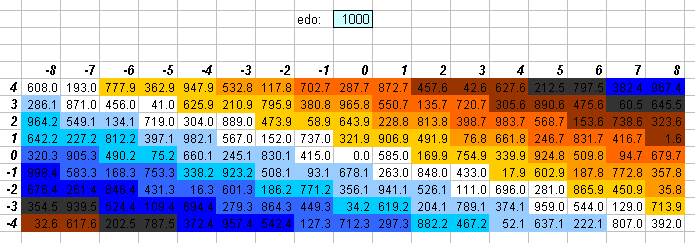
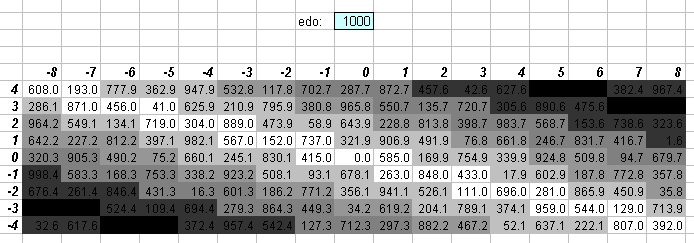
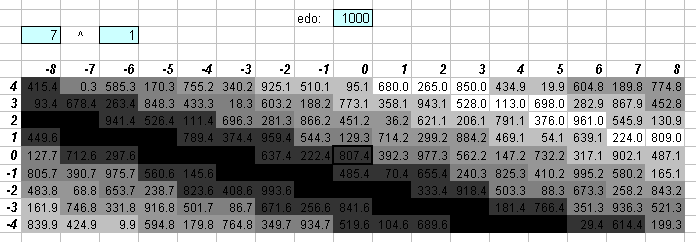
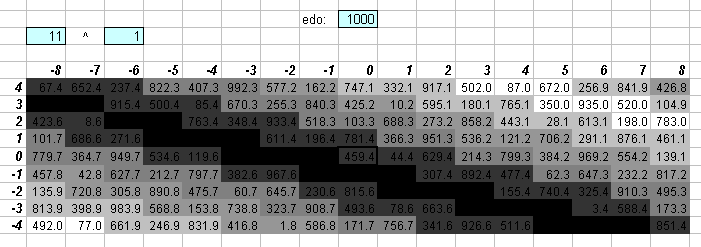
One degree of 1000edo is the unit of interval measurement called the millioctave, used prominently by Mark Lindley in Mathematical Models of Musical Scales (1993).
1024edo

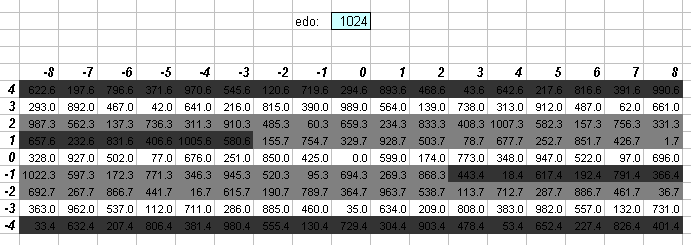
1024 edo is the tuning resolution of many popular electronic instruments, including the Yamaha DX, SY and TG series.
Below is a much larger section of the 5-limit lattice, 3^(18...19) * 5^(-17...18). The numbers are too small to read, but more colors can be seen giving a better idea of the overall pattern.
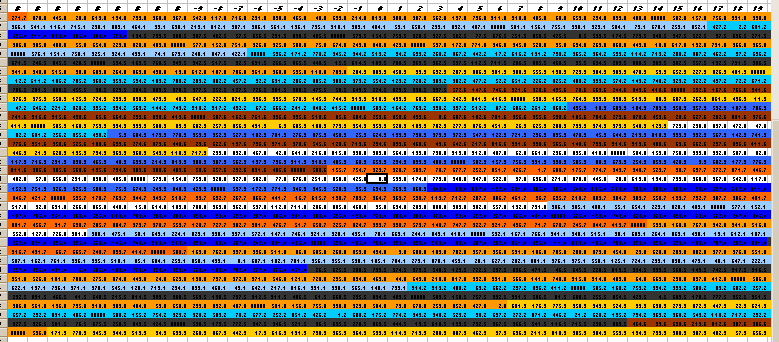
1060edo
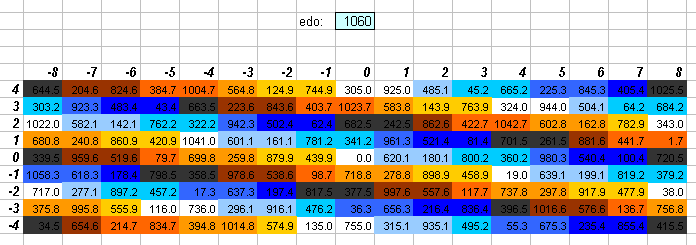
1060edo = 20 * 53edo. It is the Turkish analogue of cents; i.e., the small interval used as a basic reference measurement in Turkish music-theory.
1200edo

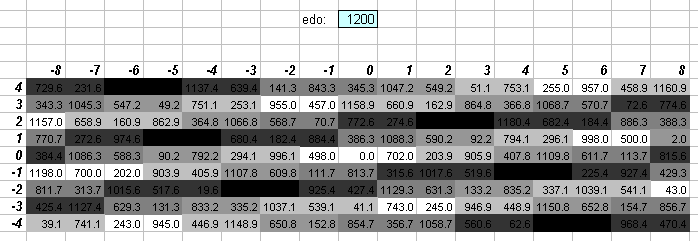
1200edo is the unit of interval measurement called cents, established by Alexander Ellis and nearly universally used today. It can be easily seen here that to use only integers, cents, while quite good for Pythagorean intervals, are not as accurate for measuring 5-limit tuning as either 612 or 730edo, or indeed even 118edo. Its adoption was primarily a matter of convenience, because it divides each degree of the standard 12edo scale into 100 units. 1200edo is also the standard measurement used by Johnny Reinhard with his American Festival of Microtonal Music (AFMM) ensemble, to train his performers to be able to handle any microtonal tuning.
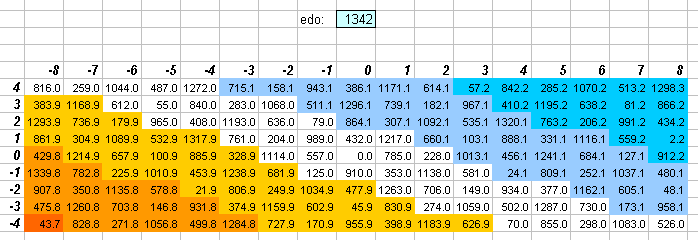
1342edo
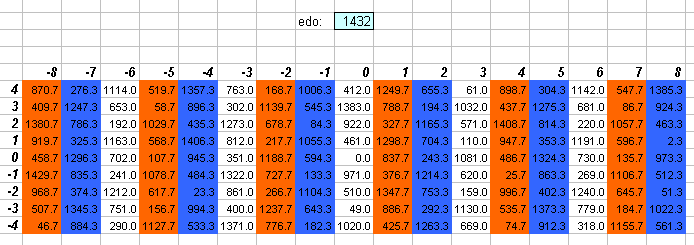
1432edo
4296edo
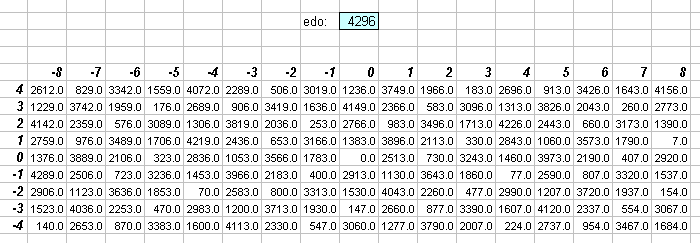
4296edo results in what is visually a very boring lattice, because it's the magic number which, as Marc Jones discovered, gives a huge central section of the 5-limit lattice -- 3(-20...20) * 5(-9...9) is a representative square chunk -- with practically zero error.

The lattice above is a "zoomed out" view of a huge 3(-32...32) * 5(-12...12) 5-limit lattice -- the numbers are far too small to be legible (in fact in zooming out so far the spreadsheet made most of them invisible!), but the pattern of grey shading can be seen in the upper left and lower right corners, showing that the error pattern for 4296edo is somewhat similar to that for 612edo, the previous winner for excellence in 5-limit approximation.
49152edo = 12 * 212
c.gif)
49152edo, which i find much easier to remember as (12 * 212)edo, is the tuning resolution for pitch-bend data for the popular computer-music program CakewalkTM, one degree of which i call a cawapu.
[from Joe Monzo, JustMusic: A New Harmony.
Thanks to John Chalmers, Manuel Op de Coul, Margo Schulter,
and especially Paul Erlich,
for helpful criticism and additional info.]
[Note from Monzo: the base is 2 only in 'octave'-equivalent equal-temperaments.
It is possible to construct an equal temperament using any number as
a base, as noted below. An example would be to divide the 'perfect 12th',
which has the ratio 3:1, into equal 'steps' (as in the
Bohlen-Pierce
scale); this is a geometric
series where each degree is a logarithm to the base
3n.]
Because of the physiology of the human
auditory system, the successive intervals of Equal Temperaments sound
perceptually equal over most of the audible range.
It is also possible
to divide intervals other than the octave as in the recent work of Wendy
Carlos (Carlos,1986), but musical examples are still rather uncommon.
[from John Chalmers, Divisions of the Tetrachord]
Any tuning system which divides the octave (2/1) into
n
aliquot parts is termed an
n-tone Equal Temperament.
Mathematically, an Equal Temperament is a geometric series and each degree is a
logarithm to the base
2n.
Updated:
2002.10.12 -- added standard deviation graph, "periodicity of intervals" 12edo lattice, 65 and 183edo entries
2002.10.09 -- added bingo-card "how x-edo really works" lattices
2002.10.06 - added bike-chain graphs for 12, 24, 36, 72, 152, and 217edo.
2002.09.16 - links to Huygens-Fokker site, corrections from Paul Erlich on first diagram
2002.09.13 - many new names and links added to list
2002.06.20
2002.02.14-18
2002.01.25