bingo-card lattice
A type of lattice diagram used to represent equal-temperaments, in which the basic prime-axis interval in each dimension of the lattice (i.e., 1 "step"of that dimension) is rounded to its nearest EDO-degree representation, then those basic values are added to and subtracted from each other, to fill out all the other EDO-degree numbers on the lattice.
This process results in a periodic tiling of periodicity-blocks across the lattice, each block containing all or some of the degrees of the EDO (depending on how big the EDO is and whether or not it is a multiple of a lower-cardinality EDO), in a pattern which thus is not random, but which at first glance appears to be random, and which in the case of a 2-dimensional lattice (like the 5-limit ones shown on this page) resembles the cards used to play the popular gambling game of bingo. As far as i know, the application of the name "bingo-card" was the idea of Paul Erlich, and the earliest author i know to have used them prominently was James McCartney.
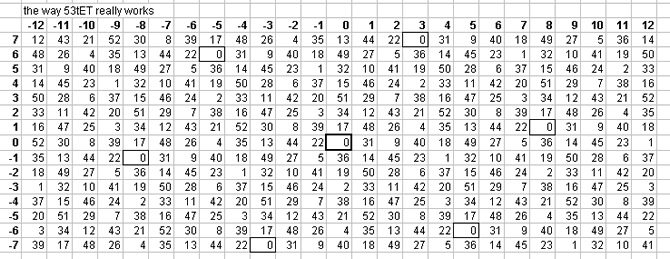
Most often, the resulting degree-numbers in a bingo-card lattice are slightly different from those obtained by merely finding the closest EDO-degree which can approximately represent the just intonation ratios. The amount of error between these two methods depends on the cardinality of the EDO under consideration, and also on the size and shape of the lattice, as different EDOs approximate JI intervals in different ways. The amount of error can be seen occurring on the bingo-card lattice in patterns, and these patterns echo, more broadly, the patterns in my lattices -- of the nearest EDO approximation to just intonation. For an example of an EDO without appreciable error, see 53edo below.
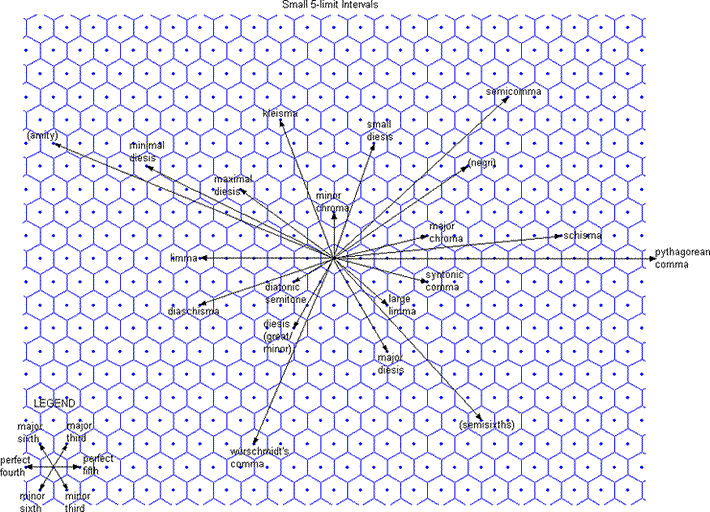
The utility of the bingo-card lattices lies in their ability to show the "vanishing commas", i.e., the small intervals which are tempered out in a particular EDO. Below is a lattice using triangular geometry,
resulting in a hexagonal cell representing each lattice-point, showing many of these intervals, with most of the more important ones labeled with the names in common use among tuning theorists c. 2000.
Small 5-limit intervals, hexagonal
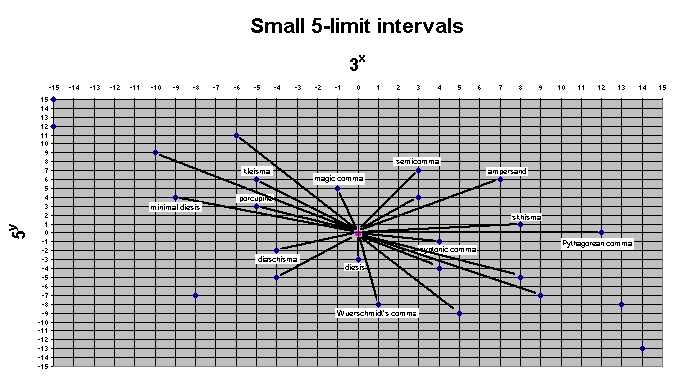
Below is a rectangular lattice showing the same thing -- this is the format used on the other lattices on this page.
Small 5-limit intervals, rectangular
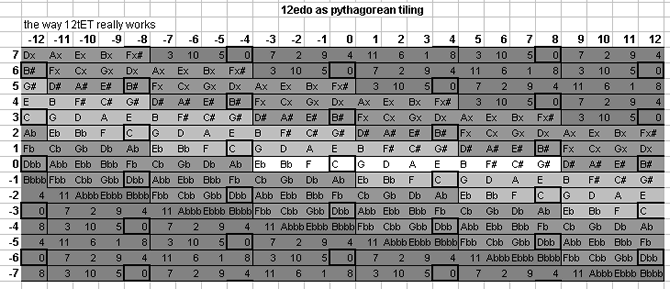
The bingo-card lattice for 12edo will be explained in detail as an example; the technique used in creating that lattice applies for all the others.
12-tone scale, 12edo
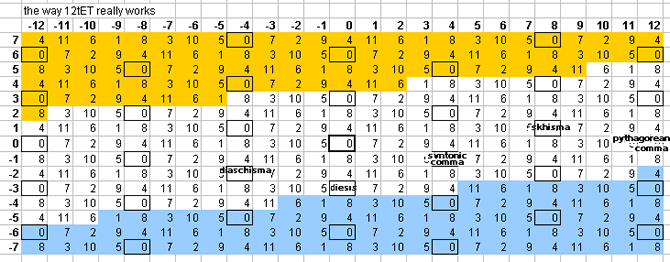
These lattices all represent equal-tempered approximations to an arbitrarily large subset of the theoretically infinite 5-limit just-intonation tuning. They assume 8ve-equivalence and thus do not have any representation of prime-factor 2, and thus represent a 2- rather than 3-dimensional prime-space (or tonespace). (The 3 prime-factors of the 5-limit are 2, 3, and 5, so viewed in its entirety it is 3-dimensional.) The whole system is an Euler-genus which can be described compactly as 3(-12...+12) · 5(-7...+7). The row of numbers across the top of each lattice designates the exponents of prime-factor 3, and the column of numbers along the left edge designate the exponents of prime-factor 5. The periodicity of the 5-limit "vanishing commas" (within the arbitrary limits described above) in 12edo can be seen on this "bingo-card" lattice:
how the 12-tone scale really works
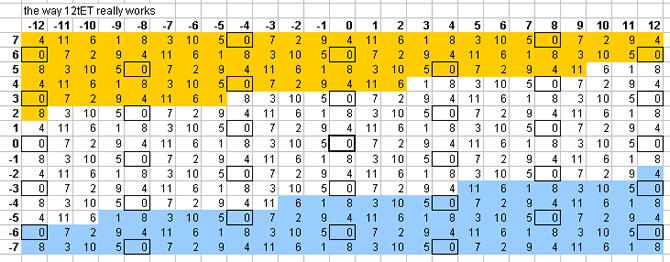
The 1/1 at the center of the lattice is represented by the reference tone, which in 12edo will be labelled as zero degrees, and on the graphic is outlined in heavy black. It can be seen that:
- looking just to the right of the center cell, the 3/2 ratio, designating the musical interval of the "perfect 5th", written in [3 5]-prime-factor vector notation as the [1 0] monzo, is represented by 7 degrees of 12edo;
- the 5/4 ratio, designating the interval of the "major 3rd", in vector format [0 1], is represented by 4 degrees of 12edo, and occupies the cell just above the central one.
- All other degrees are obtained by adding (going to the right on the lattice) or subtracting (going to the left) 7 mod 12 along the horizontal (i.e., 3) axis, and by adding (going up) or subtracting (going down) 4 mod 12 along the vertical (i.e., 5) axis.
prime-factor vectors
2 3 5 ratios
[ 7/12] ≡ [1 0] 3/2 "perfect 5th"
+ [ 7/12] ≡ + [1 0] * 3/2 "perfect 5th"
--------- -------- -----
[14/12] ≡ [2 0] 9/4 "major 9th"
and since the lattice is considered to be 8ve-invariant, and so a "major 9th" is equivalent to a "major 2nd", then just as
- 9/4 ≡ 9/8,
- so 2( (14 mod 12) / 12) = 2(2/12),
- and so 2(14/12) ≡ 2(2/12).
Thus, the 12edo degree "2", designating the interval 2(2/12), is placed in the cell representing 9/8 = [2 0], which is just to the right of the cell representing 3/2 = [1 0].
For another, slightly more complicated example, let's fill in the cell a "minor-3rd" above the reference 1/1 = [0 0]. The "minor 3rd" is ratio 6/5, which is 31 * 5-1, or a "perfect 5th" minus a "major 3rd":
prime-factor vectors
2 3 5 ratios
[ 7/12] ≡ [1 0] 3/2 "perfect 5th"
- [ 4/12] ≡ - [0 1] ÷ 5/4 "major 3rd"
--------- -------- -----
[ 3/12] ≡ [1 -1] 6/5 "minor 3rd"
Thus, the 12edo degree "3" is placed in the cell representing 6/5 = [1 -1]. And so on.
Eventually (because of the incommensurability of prime-multiples), for every EDO, a point will be found where the just ratio is better represented by another EDO-degree different from the one found by this process of vector-addition. As an example, let's examine the 12edo representation of successive "major 3rds", which are the degree-numbers above the bold-outlined zero in the central column. In the yellow cell representing [0 4], which designates 54, the bingo-card lattice above has "4", meaning 4 degrees of 12edo (mathematically 2(4/12)), derived from successive addition:
12edo cents interval ratio cents of ratio error of 12edo
0 0 prime (1me) 1/1 0 0
+ 4 + 400 major-3rd * 5/4 + 386.3137139
--- ------ -------- ---------------
4 400 major-3rd 5/4 386.3137139 + 13.68628614
+ 4 + 400 major-3rd * 5/4 + 386.3137139
--- ------ -------- ---------------
8 800 augmented-5th 25/16 772.6274277 + 27.37257227
+ 4 + 400 major-3rd * 5/4 + 386.3137139
--- ------ -------- ---------------
12 1200 augmented-7th 125/64 1158.941142
mod 12 - 1200 "8ve"-reduce * 1/2 - 1200
------ ------ -------- ---------------
0 0 125/128 -41.05885841 + 41.05885841
+ 4 + 400 major-3rd * 5/4 + 386.3137139
--- ------ -------- ---------------
4 400 doubly-augmented-2nd 625/512 345.2548555 + 54.74514454
compare that result with 3 degrees of 12edo:
3 300 doubly-augmented-2nd 625/512 345.2548555 - 45.25485546
2(4/12) represents 54 with an error of +~54 3/4 cents. But the table shows that 3 degrees (= 2(3/12)) provides a closer approximation, with an error of -~45 1/4 cents. To find the fractional value that shows the nearest 12edo approximation, one may simply divide the cents-value by 100, to obtain ~3.452548555 Semitones, which does indeed show that 3 degrees is a closer approximation than 4.
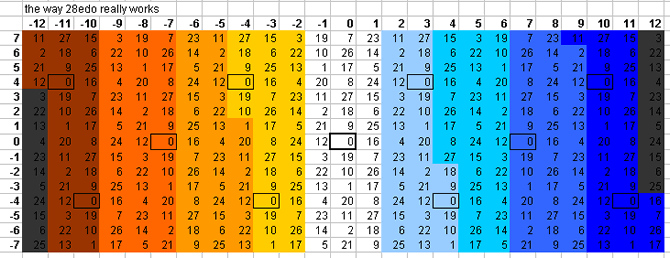
Where a 12edo degree on the bingo-card lattice is different from the nearest 12edo approximation of the corresponding ratio in the just lattice, those lattice-cells are colored: yellow where the 12edo note is 1 degree too high, and blue where it is 1 degree too low. Thus, the cell just examined is yellow because its 12edo approximation to the "doubly-augmented-2nd" is 4 degrees of 12edo instead of the closer approximation of 3 degrees. The legend is as follows:
bingo-card error
The cells outlined in black are all the instances of 2(0/12), which shows immediately which of the commas vanish (as per the graph given above), and thus the periodicity. This lattice shows that 12edo tempers out a large number of small 5-limit intervals, including:
- the syntonic comma, designated in [3 5] prime-factor vector-notation by the monzo [4 -1], (making 12edo function as a meantone, specifically 1/11-comma meantone),
- the diaschisma [-4 -2],
- the diesis [0 -3], and also
- the skhisma [8 1],
- the Pythagorean comma [12 0],
and others which can be found by adding together various combinations of the syntonic comma, diaschisma, and diesis. Here is the same lattice shown above with these 5 unison-vectors labeled:
12edo bingo card with primary unison vectors labeled
12edo does not temper out the kleisma, porcupine comma, magic comma, semicomma, or ampersand's comma. Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 12edo (this is precisely the same as Hindemith's 5-limit JI derivation of 12-ET):
enharmonic tiling of the 12edo tuning
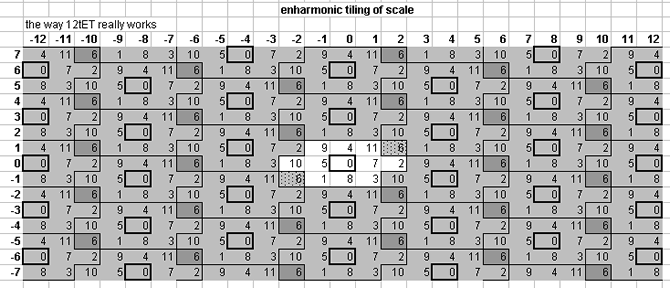
In this and all of the "tiling" lattices below, the objective was to outline the periodicity-blocks which forms the source-cell at the center of the lattice -- i.e., all ratios as close as possible, by the taxicab metric, to the 1/1 at the origin point. In many cases, one or more EDO representations of ratios may be the same distance from 1/1, and so they must belong to multiple tiles simultaneously.
Anyway, this is trivial, because the unison-vectors bounding the periodicity-block may be moved incrementally along either the 3- or 5-axis or both, so that the source periodicity-block encloses entirely and uniquely only the exact number specified by the cardinality of the EDO, without changing the essential nature of that particular periodicity-block other than to eliminate duplicate pitches at the boundaries. Thus, in 12edo, we would obtain either a periodicity-block which includes a representation of the "augmented 4th" ("tritone", ratio 45:32, 3,5-monzo [2, 1> ) but not the "diminished 5th" (this is the Malcolm monochord scale):
periodicity block containing the augmented 4th
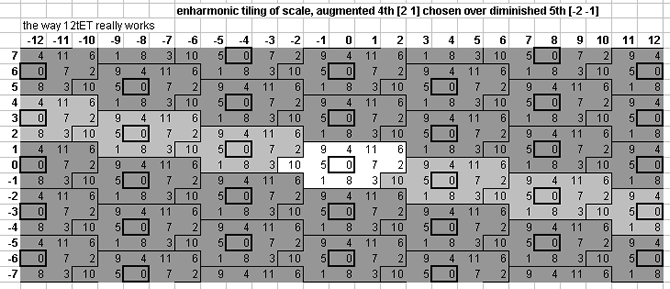
... or alternatively, one which includes the "diminished 5th" (ratio 64:45, 3,5-monzo [-2,-1> ) but not the "augmented 4th":
periodicity block containing the diminished 5th
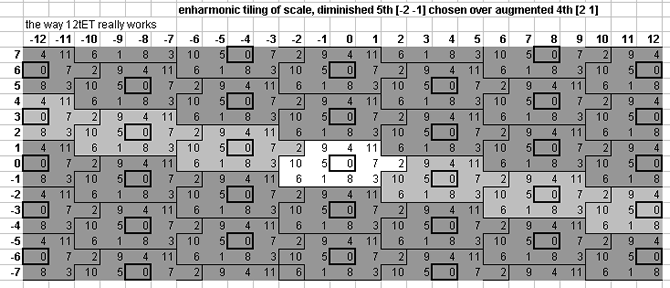
Of course, in actuality 12edo represents both of these ratios simultaneously, because they are a diaschisma apart and this is one of the commas which vanishes in 12edo.
12edo is very often used as a pseudo-Pythagorean aristoxenean temperament, in a cycle with letter-names from Eb to G#. Below is a lattice showing this mapping, but this time substituting letter-names for degree-numbers for all those which would be found in the standard repertoire (degree-numbers for the rest), and showing enharmonic equivalents as darker shades of grey:
12edo as a pseudo pythagorean aristoxanean scale
12edo gives excellent representations of the Pythagorean prime-factor 3 (~ -2 cents error), and of 19 (~ +2.5 cents error) and 17 (~ -5 cents error). 12edo's best representations of 5 and 43 are mediocre, those of 7, 13, 23 and 29 quite poor, and those of 11, 31, and 37 terrible, 11 and 37 lying basically midway between two 12edo degrees (50% EDO-step error is the exact midpoint):
12edo prime error
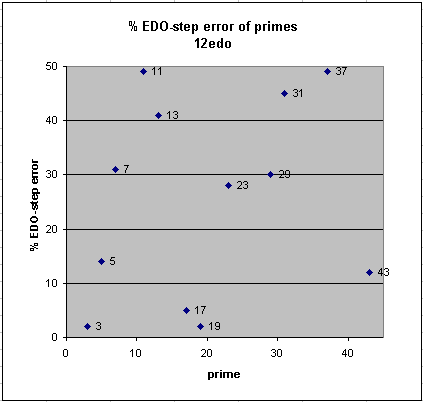
12edo best representation
of prime-factor
prime ~cents error % error
3 -1.955000865 -2
19 +2.486983868 +2
17 -4.9554095 -5
43 -11.51770564 -12
5 +13.68628614 +14
23 -28.27434727 -28
29 -29.57719415 -30
7 +31.17409353 +31
13 -40.52766177 -41
31 -45.03557246 -45
11 +48.68205764 +49
37 +48.65596125 +49
5-Limit Bingo Card Viewer
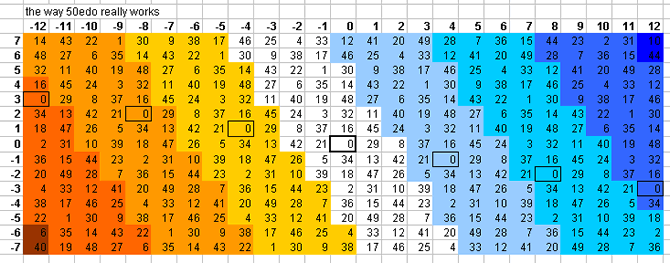
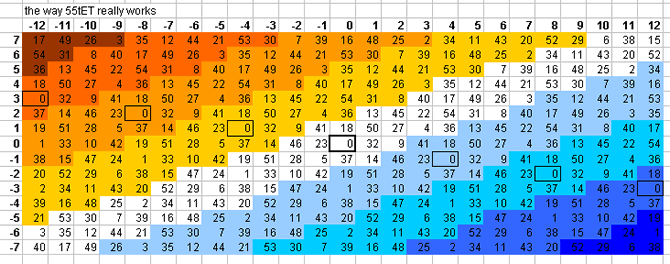
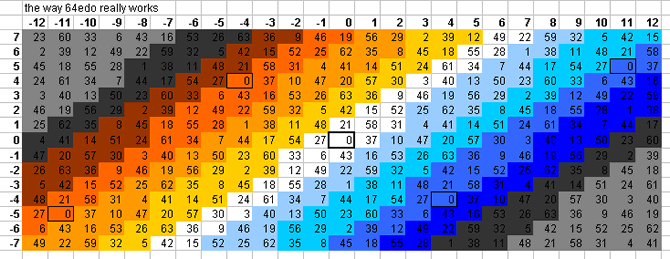
Click on one of the following links to see the 5-limit bingo-card for that EDO/cardinality. Cardinalities in plain text are not available. If there is additional information, it will be displayed under the bingo-card.
10-tone bingo card
11-tone bingo card
12-tone bingo card
13-tone bingo card
14-tone bingo card
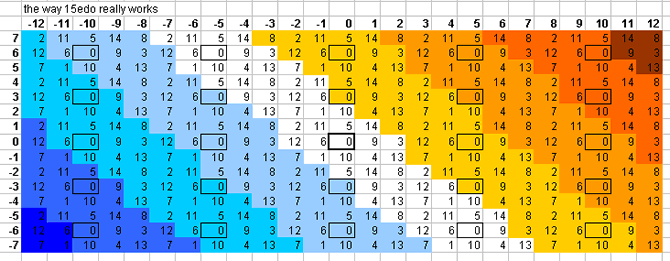
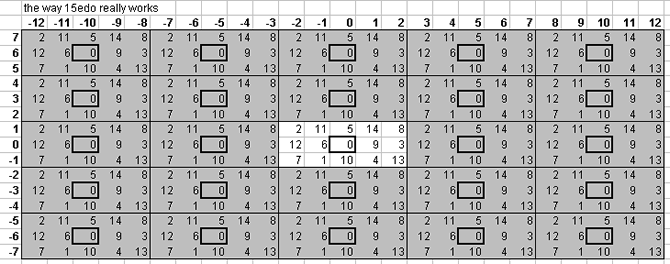
15-tone bingo card
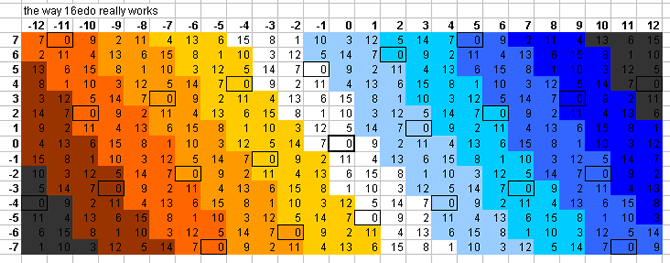
16-tone bingo card
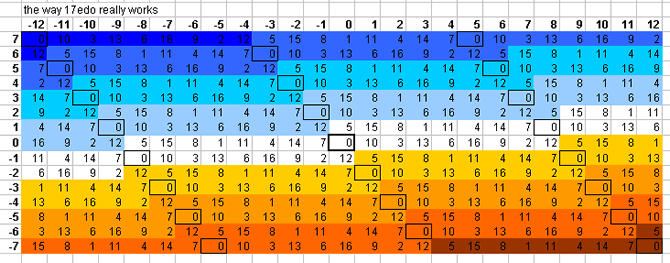
17-tone bingo card
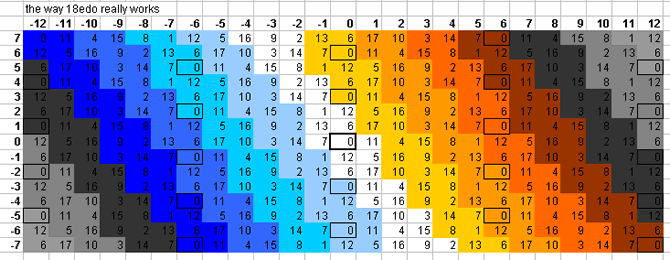
18-tone bingo card
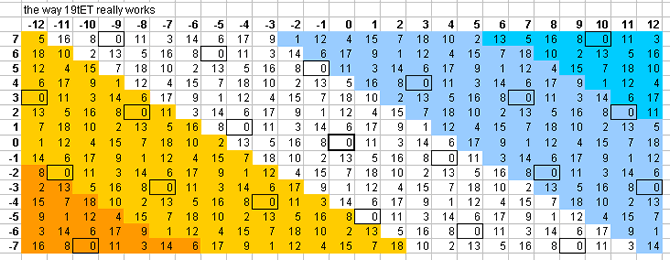
19-tone bingo card
20-tone bingo card
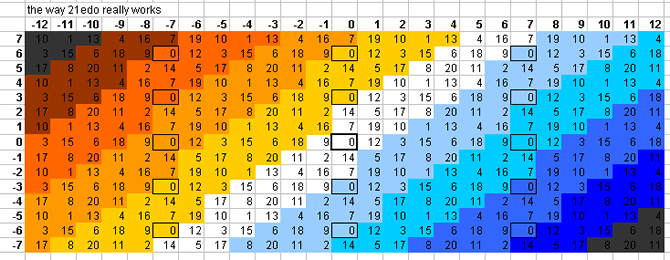
21-tone bingo card
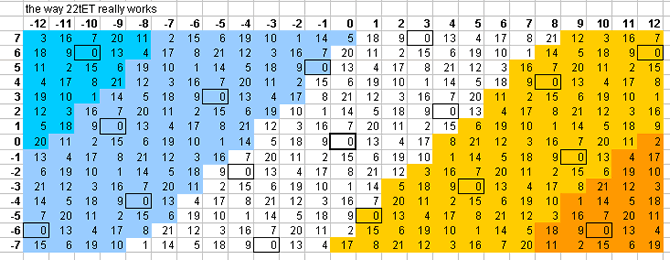
22-tone bingo card
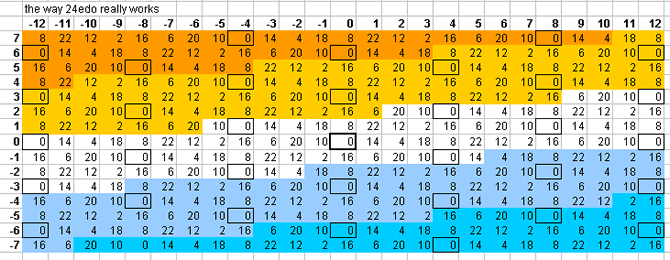
24-tone bingo card
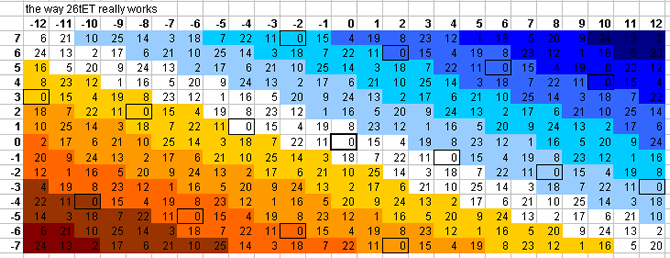
26-tone bingo card
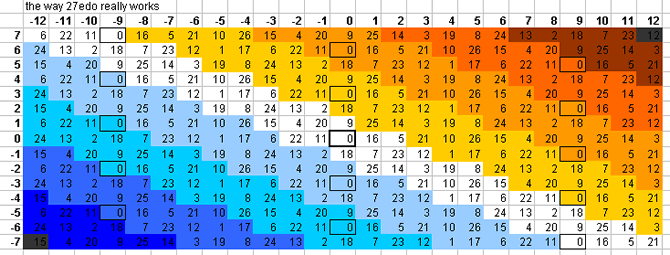
27-tone bingo card
28-tone bingo card
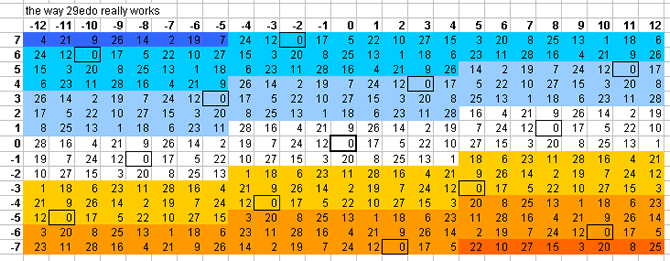
29-tone bingo card
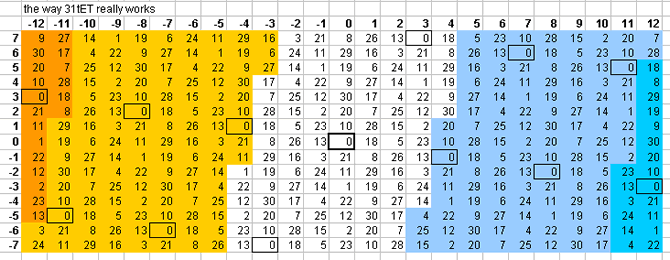
31-tone bingo card
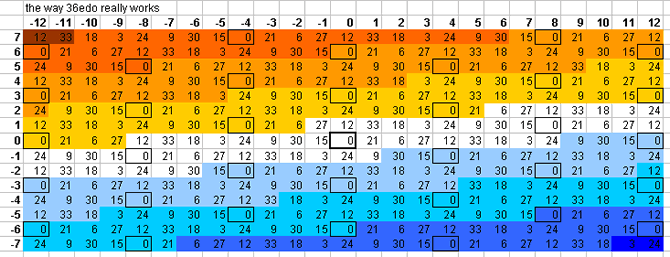
36-tone bingo card
40-tone bingo card
41-tone bingo card
43-tone bingo card
48-tone bingo card
50-tone bingo card
53-tone bingo card
55-tone bingo card
64-tone bingo card
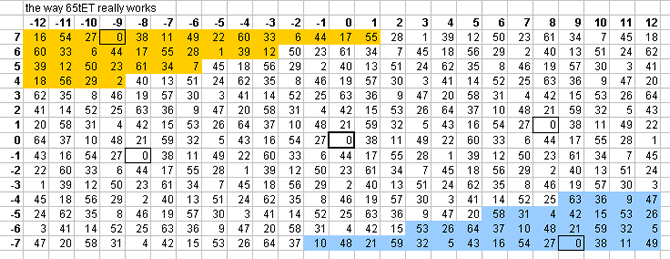
65-tone bingo card
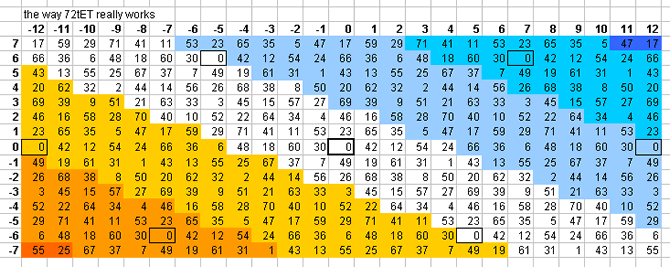
72-tone bingo card
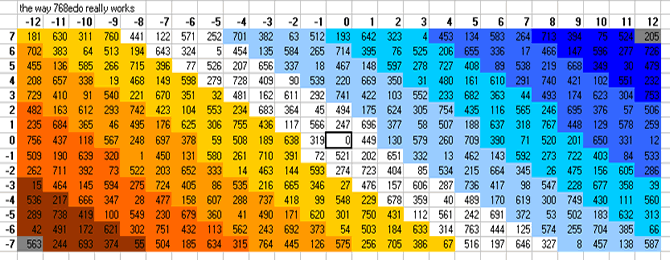
768-tone bingo card






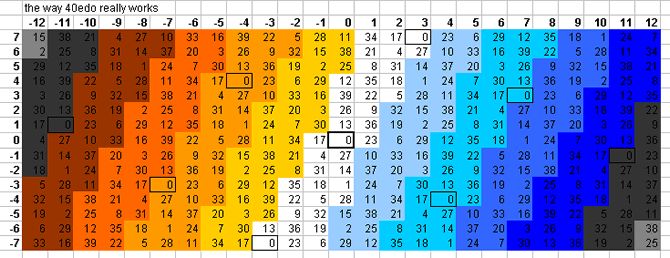
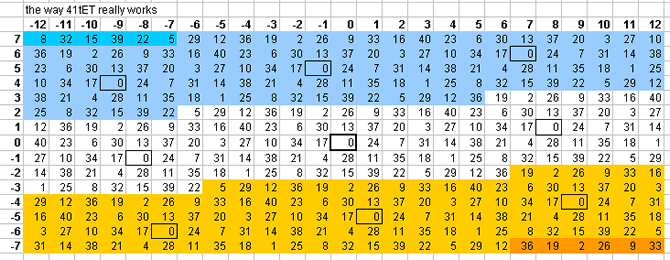
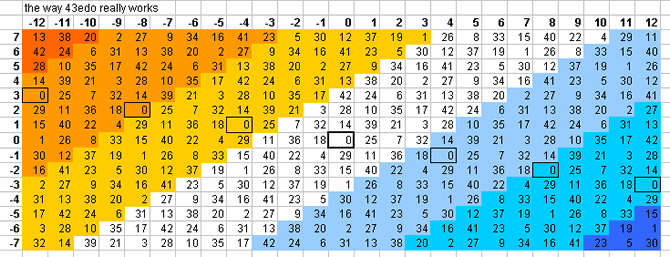
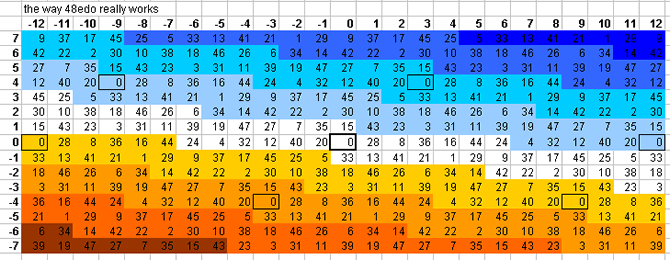
10edo gives a suberb representation of prime-factor 13 (only ~ -0.5 cent error), and fair-to-mediocre representations of 7 (~ -9 cents error), 37, 17, and 3. It does quite poorly with 5, 11, and 19.

10edo best representation of prime-factor prime ~cents error % EDO-step error 13 -0.527661769 0 7 -8.825906469 -7 37 -11.34403875 -9 17 +15.0445905 +13 3 +18.04499913 +15 5 -26.31371386 -22 23 -28.27434727 -24 43 -31.51770564 -26 11 +48.68205764 +41 29 +50.42280585 +42 31 +54.96442754 +46 19 -57.51301613 -48
11edo gives fairly good representations of prime-factors 17 and 11 (~ +4 and -6 cents error, respectively) but does a terrible job with 3 and 5 (~ -47 and +50 cents error).

11edo best representation of prime-factor prime ~cents error % EDO-step error 17 +4.135499591 +4 11 -5.86339691 -5 7 +12.99227535 +12 23 +26.27110728 +24 19 +29.75971114 +27 13 +32.19961096 +30 37 -33.16222057 -30 43 +33.93683981 +31 3 -47.40954632 -43 29 -47.75901233 -44 5 +50.0499225 +46 31 -54.12648156 -50
Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 15edo:
Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 16edo:
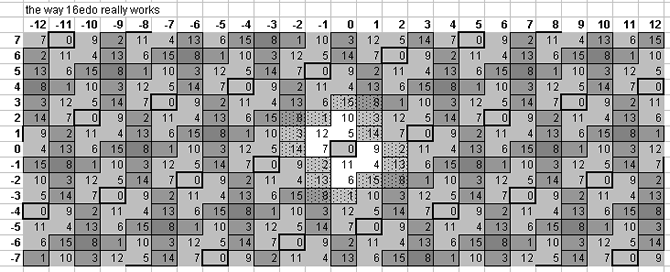
16edo tempers out the magic comma [-1 5] and also the rather large ratio 128/135 [3 1] (= ~92 cents) called "larger limma" by Ellis and "mean semitone" by Rameau, and their derivatives. 16edo tempers out neither the syntonic comma, kleisma, skhisma, diaschisma, diesis, Pythagorean comma, minimal diesis, porcupine comma, semicomma, nor ampersand's comma.
Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 17edo:
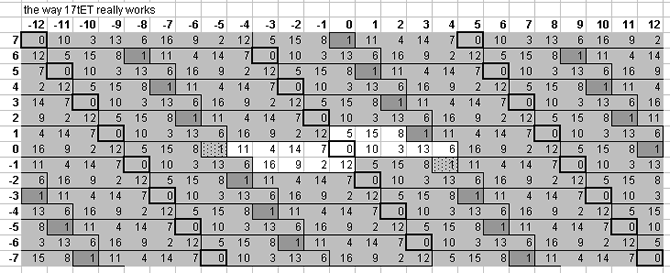
17edo tempers out the skhisma [8 1] and the 5-limit chromatic semitone [-1 2] (called "small semitone" by Ellis). 17edo tempers out neither the syntonic comma, kleisma, diaschisma, diesis, Pythagorean comma, minimal diesis, porcupine comma, semicomma, nor ampersand's comma.
Because of the fact that the 5-limit "3rds" (major and minor) are both represented by 5 degrees of 17edo, which is really a "neutral 3rd", it cannot emulate 5-limit tuning well, but rather functions primarily as a Pythagorean tuning, with 4 and 6 degrees being good representations of [-3 0] (i.e., 3-3) and [4 0] (= 34), respectively. Besides giving an excellent representation of the Pythagorean prime-factor 3 (~3.927352076 cents error), 17edo also gives good representations of 13 (~6.53116176 cents error) and 23 (~7.019770379 cents error).
Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 19edo:

19edo tempers out the syntonic comma [4 -1], causing it to act as 1/3-comma meantone; and also the kleisma [-5 6] and "magic" comma [-1 5], and others derived from those three. 19edo tempers out neither the skhisma, diaschisma, diesis, Pythagorean comma, minimal diesis, porcupine comma, semicomma, nor ampersand's comma. It does a fairly good job of representing prime-factors 3 and 5, and is mediocre with 7 and 11:
prime ~cents error 37 +1.287540193 23 +3.3046001 43 -6.254547748 3 -7.21815876 5 -7.366345444 31 -8.193467201 11 +17.10311027 19 +18.27645755 29 -19.05087836 13 -19.47503019 17 +21.36037997 7 -21.45748542
Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 22edo:
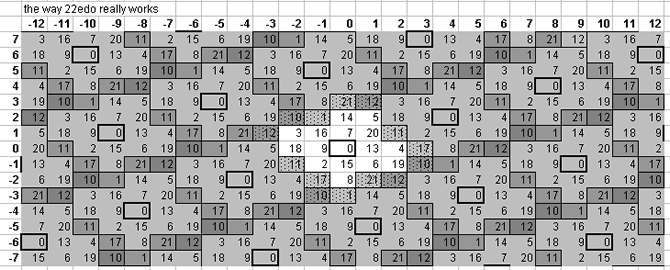
22edo tempers out neither the syntonic comma, skhisma, diesis, Pythagorean comma, or ampersand's comma. 22edo does a fairly good job of representing prime-factors 3, 5, and 11, and is mediocre with 7:
22edo best representation of prime-factor prime ~cents error 31 +0.41897299 5 -4.495532047 17 +4.135499591 11 -5.86339691 29 +6.786442211 3 +7.135908226 7 +12.99227535 13 -22.34584359 19 -24.78574341 23 +26.27110728
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
