Microtonal, just intonation, electronic music software Microtonal, just intonation, electronic music software

Encyclopedia of Microtonal Music Theory

@ 00 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Login   |  Encyclopedia Index

TM-Reduced Lattice Basis

"T" stands for Tenney [James Tenney, composer and music-theorist], "M" for Minkowski [Hermann Minkowski, mathematician]. A method for reducing the basis of a lattice. First we need to define Tenney height. if p / q is a positive rational number in reduced form, then the Tenney height is TH(p / q) = p · q. Now suppose {q1, ..., qn} are n multiplicatively linearly independent positive rational numbers. Linear independence can be equated, for instance, with the condition that rank of the matrix whose rows are the monzos for qi is n. Then {q1, ..., qn} is a basis for a lattice L, consisting of every positive rational number of the form q1e1 ... q1en where the ei are integers and where the log of the Tenney height defines a norm. Let t1 > 1 be the shortest (in terms of Tenney height) rational number in L greater than 1. Define ti > 1 inductively as the shortest number in L independent of {t1, ... ti-1} and such that {t1, ..., ti} can be extended to be a basis for L. In this way we obtain {t1, ..., tn}, the TM reduced basis of L. See this definition of Minkowski reduction and definitions by Gene Ward Smith.

[Gene Ward Smith, Yahoo tuning-math group Message 6955]
. . . . . . . . .

5-Limit Base Examples

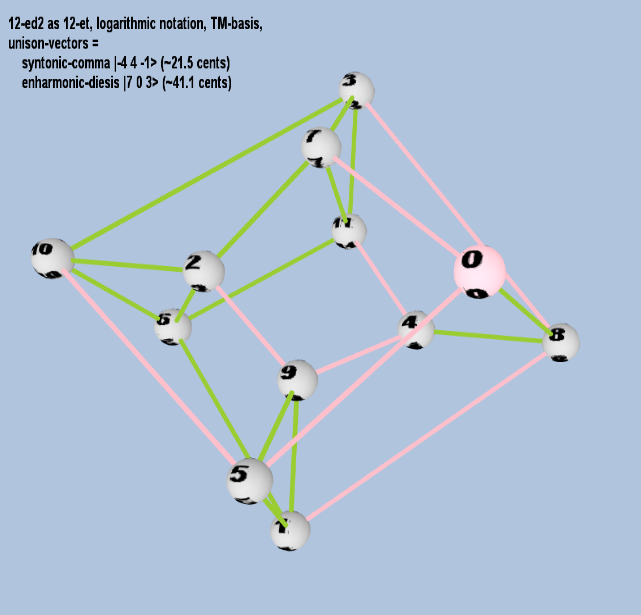
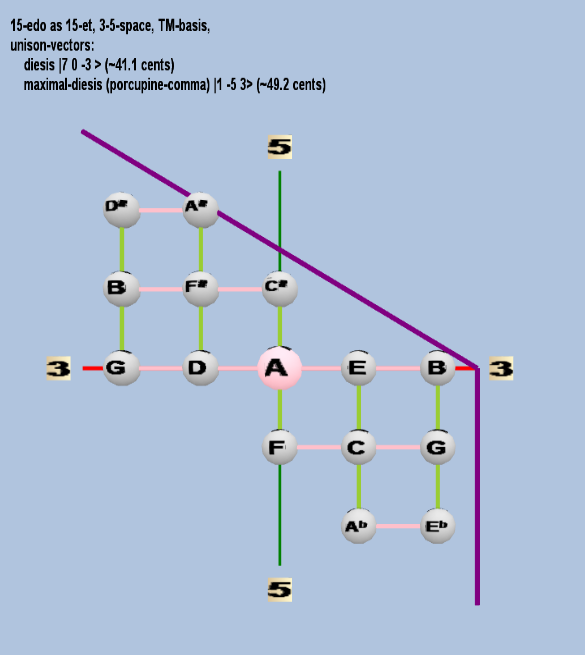
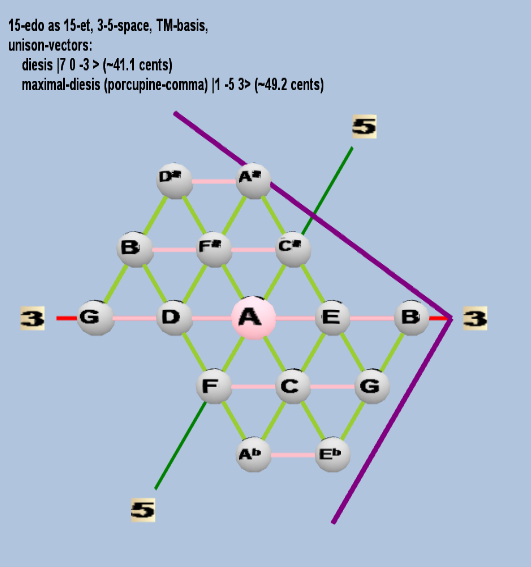
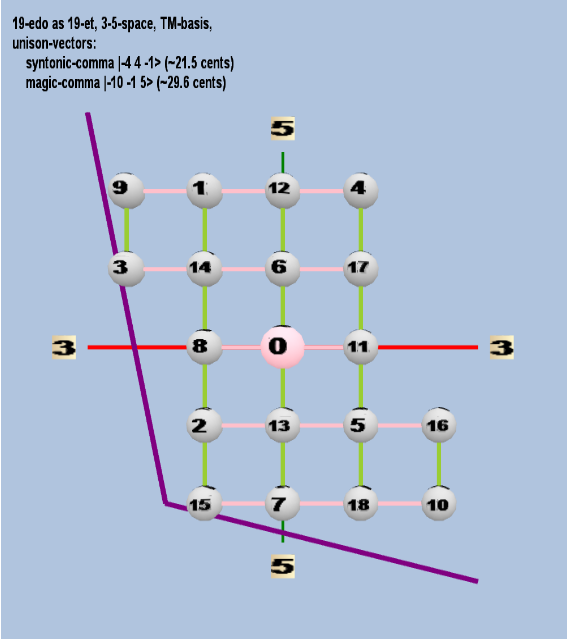
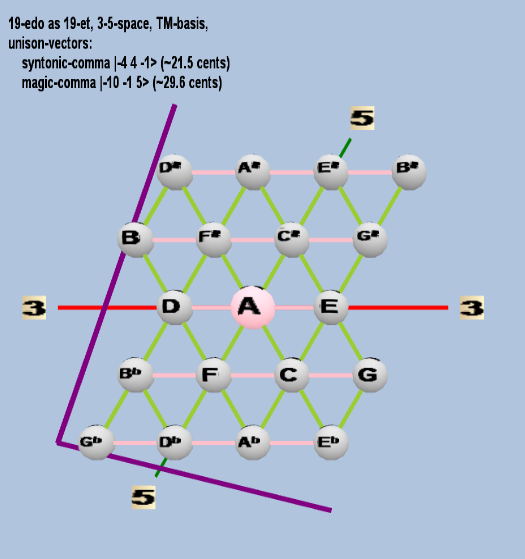
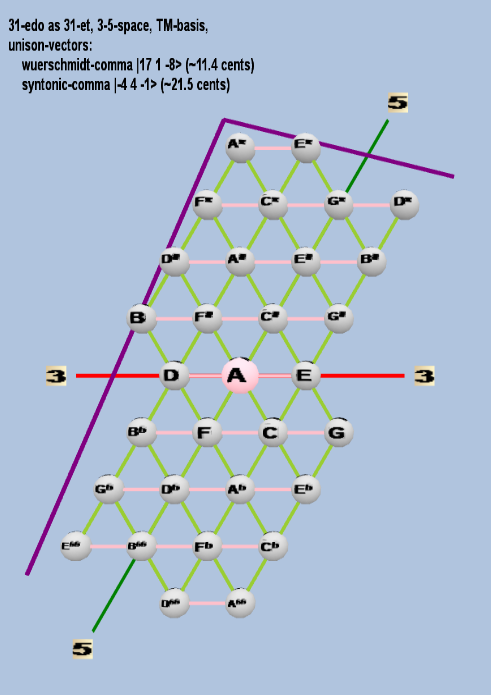
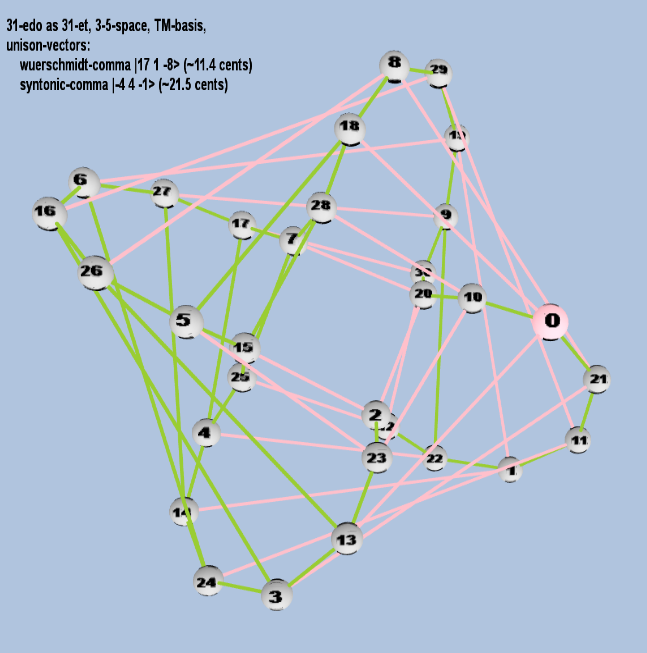
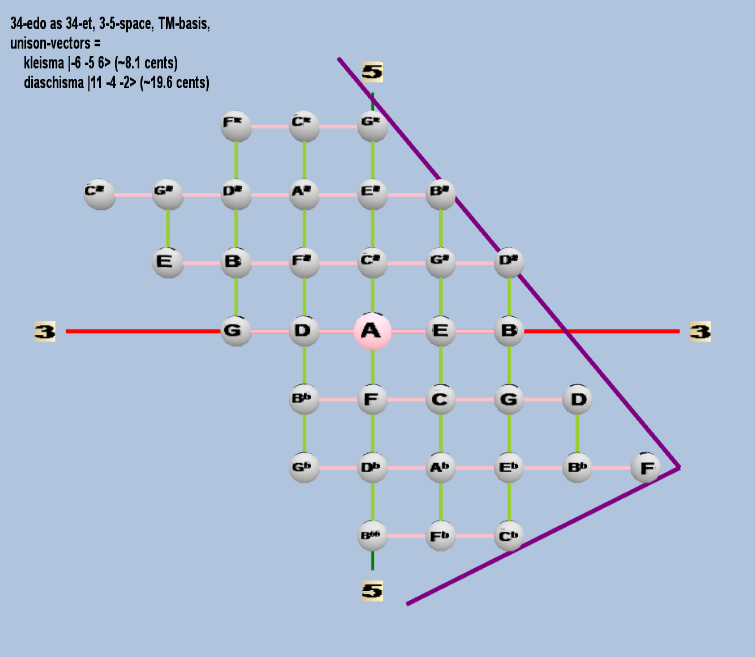
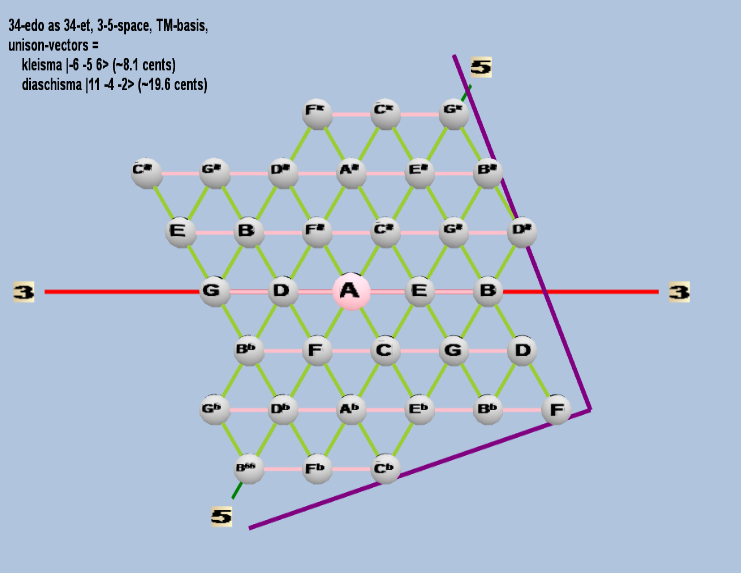
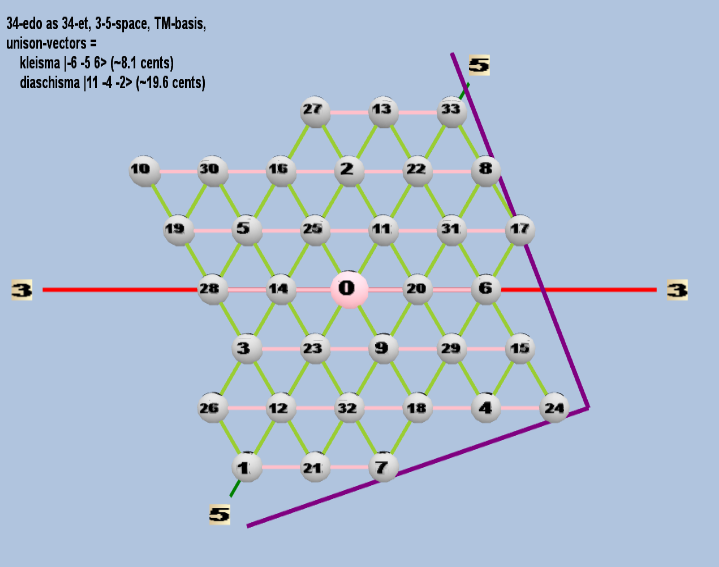
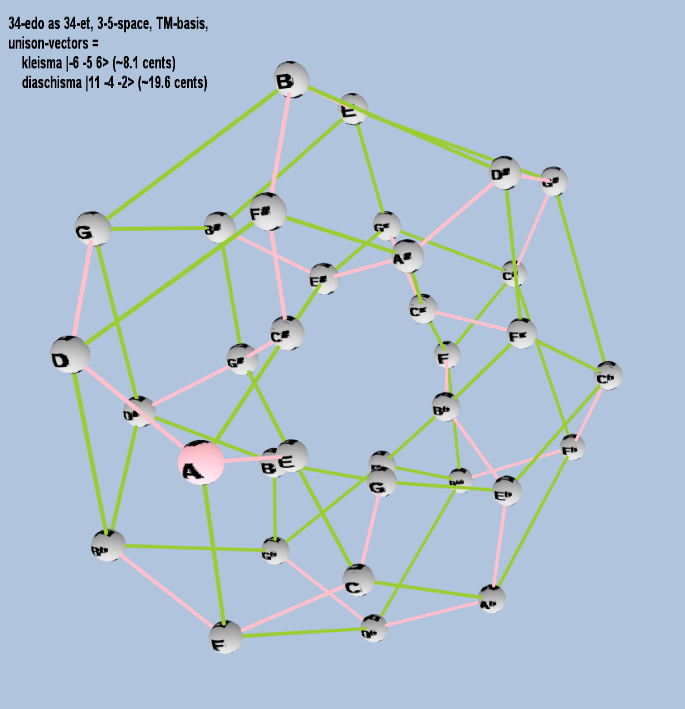
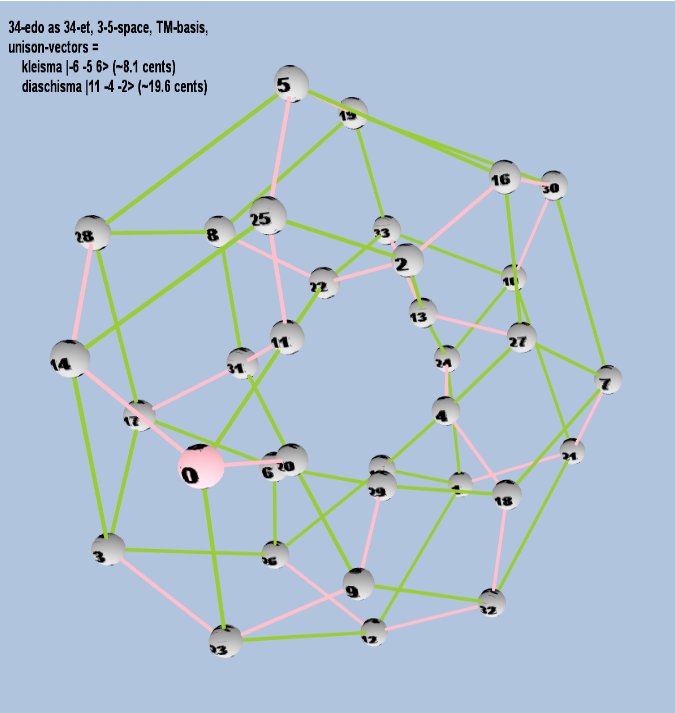
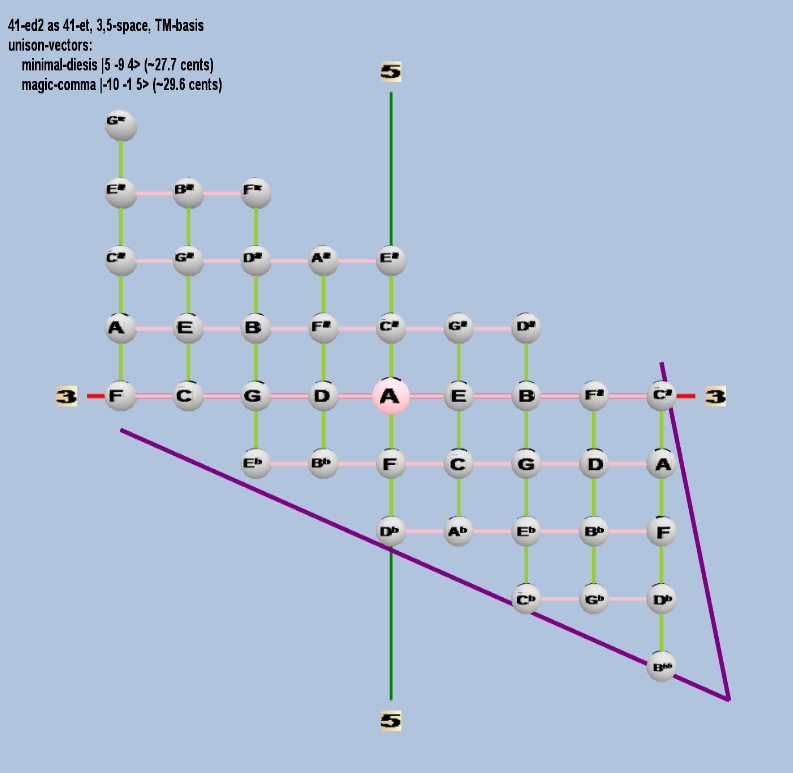
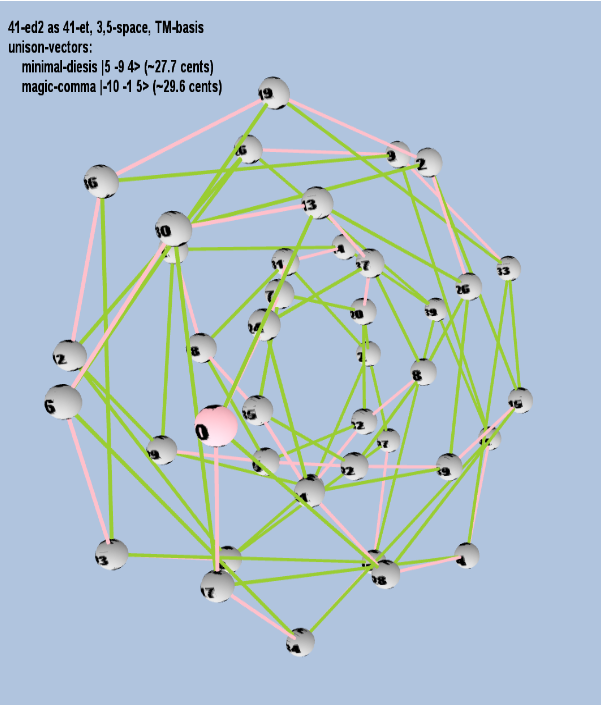
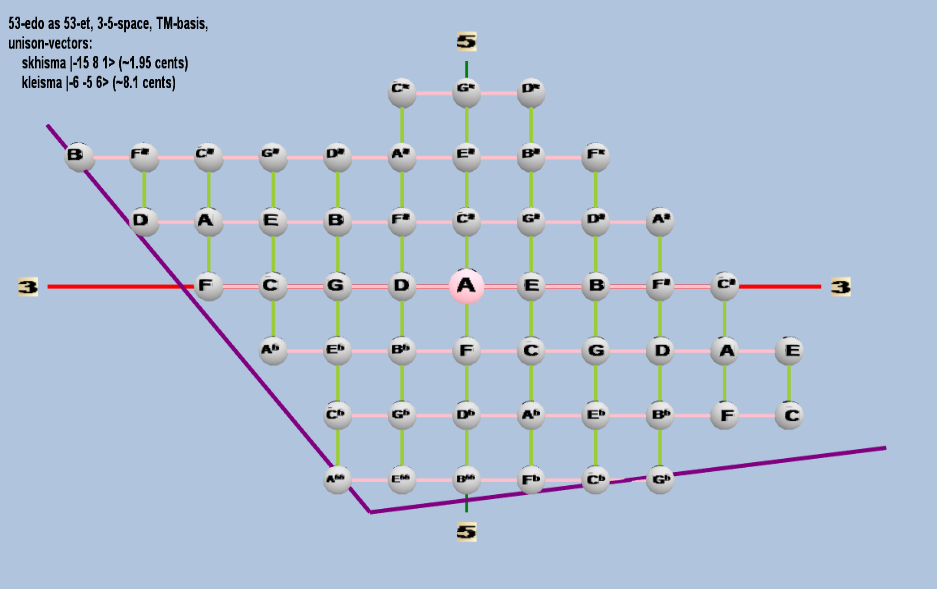
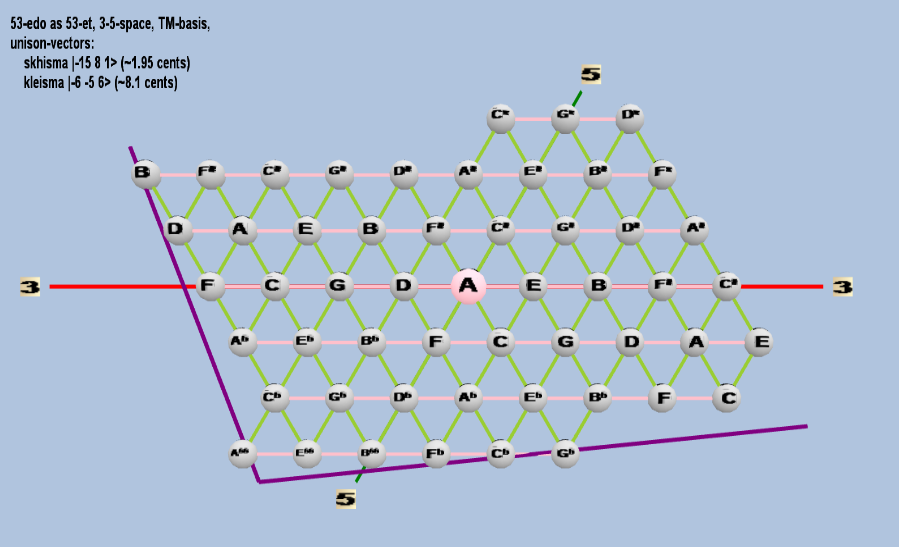
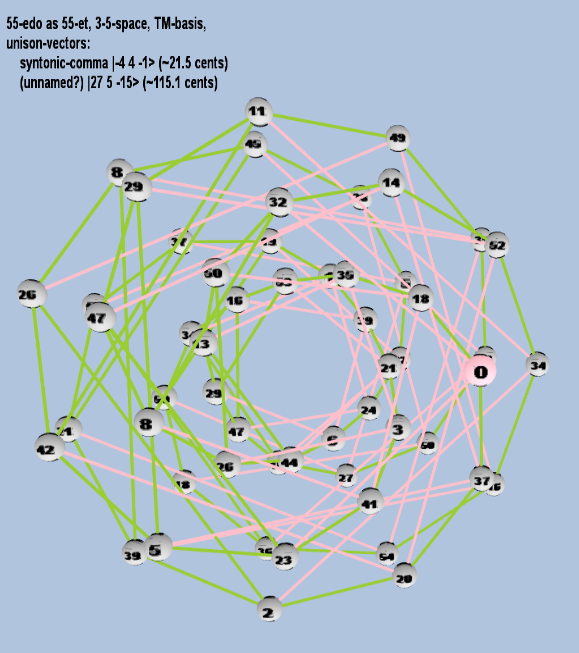
Here are some of the 5-limit TM-reduced lattice bases and the resulting periodicity blocks, rendered in Tonalsoft™ Tonescape™ software. The purple lines are the two unison-vectors which form the lattice basis, the spheres represent the exponents of the prime-factors 3 and 5, which designate the ratios in the just-intonation version of the tuning, the pink lines connect the ratios together along the 3-axes, and the green lines connect the ratios along the 5-axes, showing the periodicity-block structure. Note that in the rectangular lattices the pink connectors represent only the 3 and 5 axes, while in the triangular lattices there is also a third connector which represents an axis containing both 3 and 5: in these images these are also colored green. Note also that the toroidal lattices cannot show the unison-vectors, because in that geometry the unison-vectors are reduced to a point. (Two higher-dimensional examples are also shown at the bottom of this page.)

12 ET/EDO

name factors monzo ratio ~cents
syntonic-comma 2-4 34 5-1 [-4 4, -1> 81 / 80 21.5062896
enharmonic-diesis 27 30 5-3 [ 7 0, -3> 128 / 125 41.05885841

rectangular

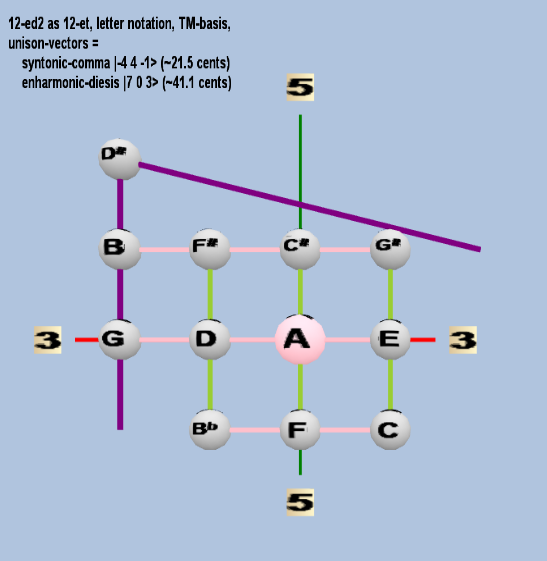
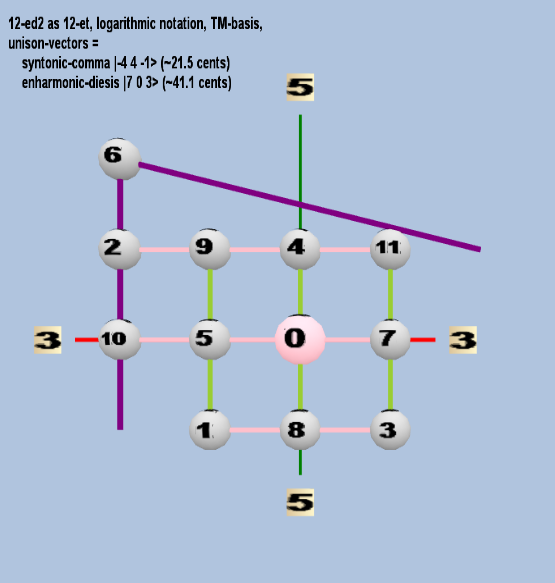
Lattice: 3,5-space, TM-basis, 12-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 12-edo, rectangular geometry, logarithmic 12-edo degree notation

triangular

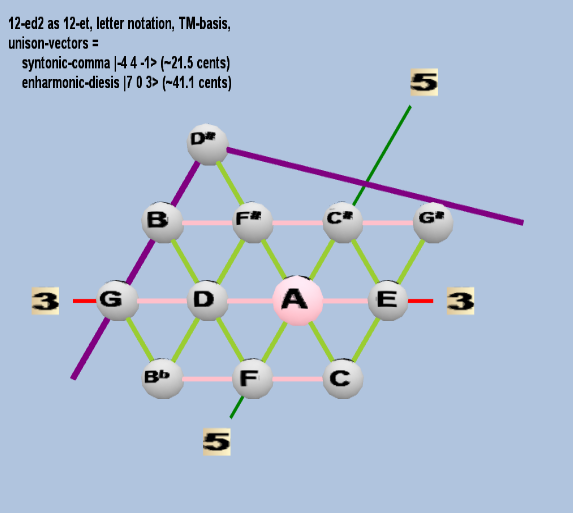
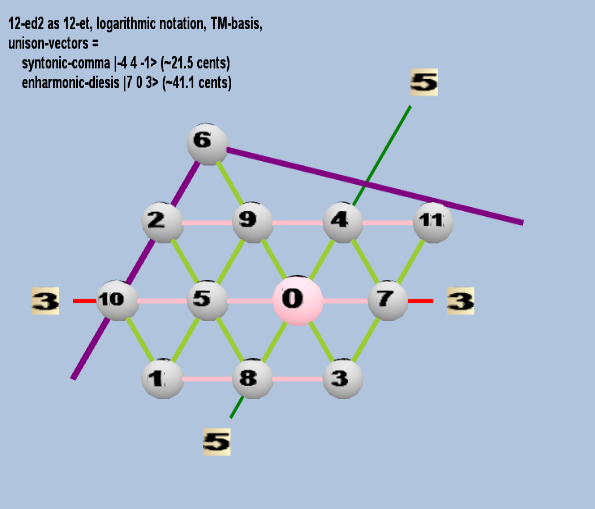
Lattice: 3,5-space, TM-basis, 12-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 12-edo, triangular geometry, logarithmic 12-edo degree notation

toroidal

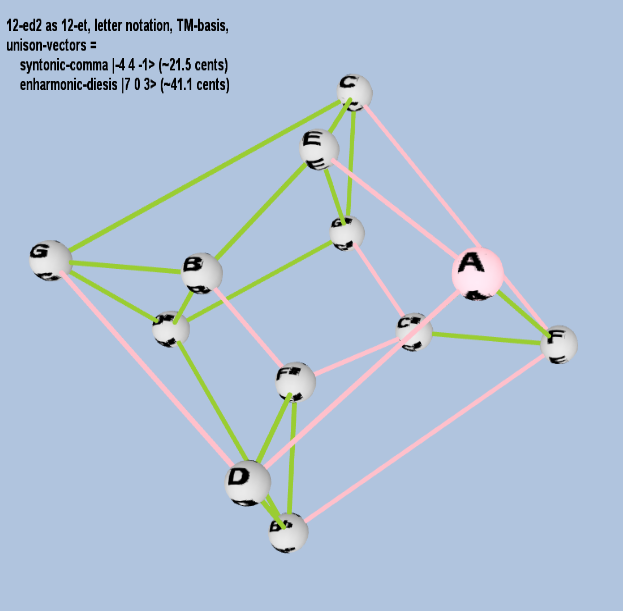
Lattice: 3,5-space, TM-basis, 12-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 12-edo, closed-curved torus geometry, logarithmic 12-edo degree notation

15 ET/EDO

name factors monzo ratio ~cents
enharmonic-diesis 27 30 5-3 [ 7 0, -3> 128 / 125 41.05885841
maximal-diesis (porcupine-comma) 21 3-5 53 [ 1 -5, 3> 250 / 243 49.16613727

rectangular

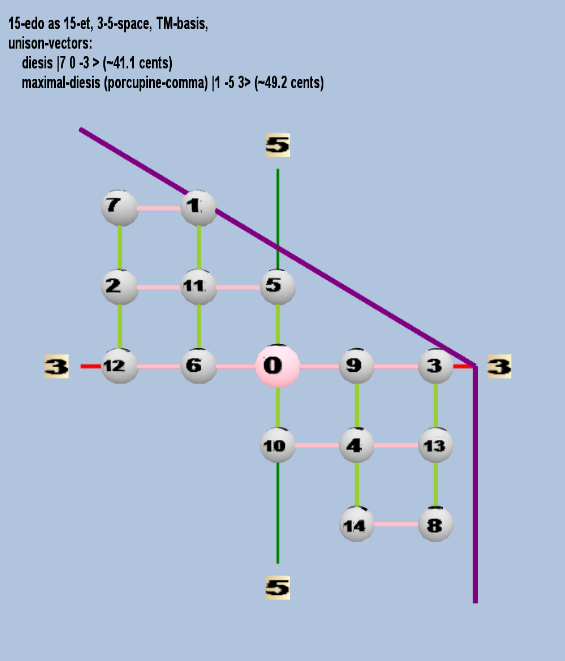
Lattice: 3,5-space, TM-basis, 15-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 15-edo, rectangular geometry, logarithmic 15-edo degree notation

triangular

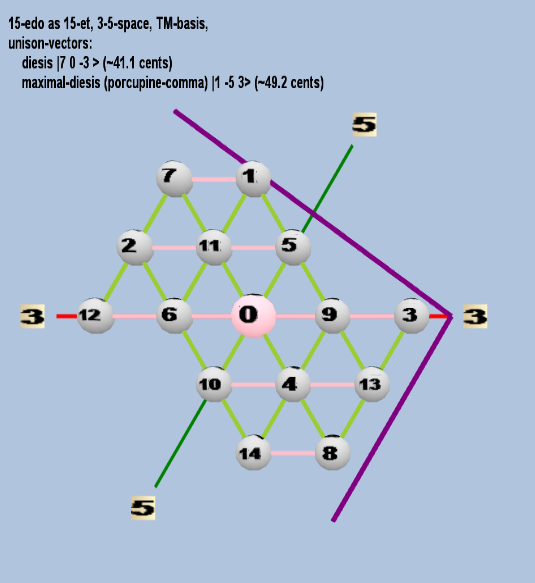
Lattice: 3,5-space, TM-basis, 15-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 15-edo, triangular geometry, logarithmic 15-edo degree notation

toroidal

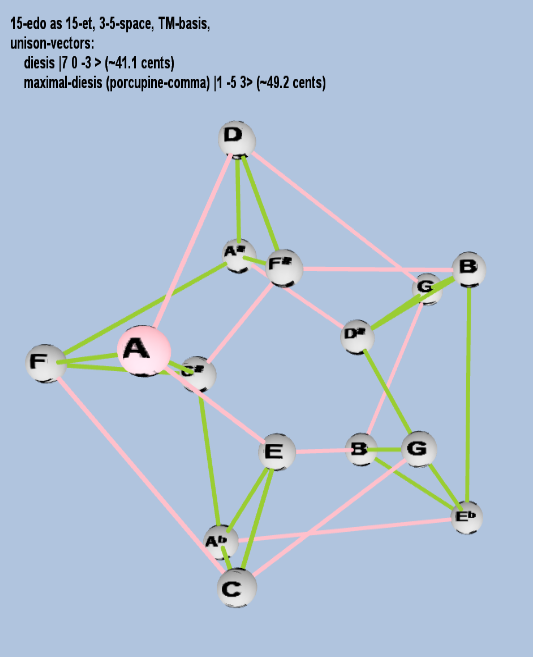
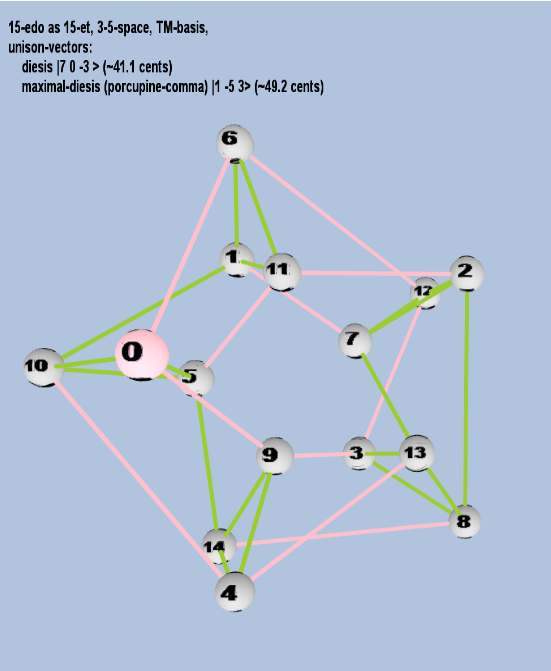
Lattice: 3,5-space, TM-basis, 15-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 15-edo, closed-curved torus geometry, logarithmic 15-edo degree notation

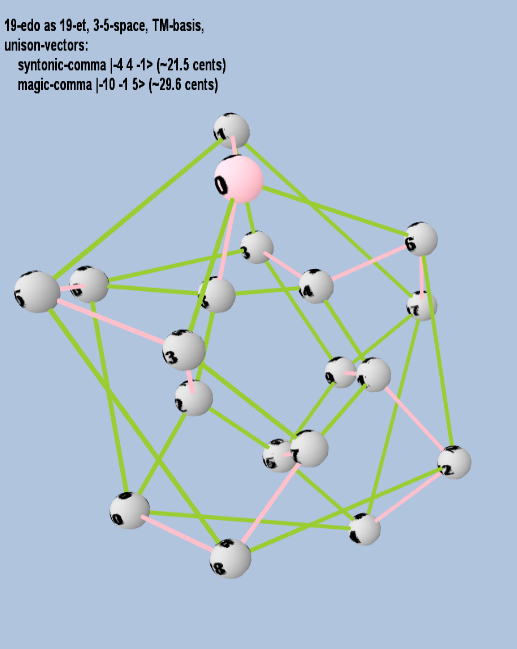
19 ET/EDO

name factors monzo ratio ~cents
syntonic-comma 2-4 34 5-1 [-4 4, -1> 81 / 80 21.5062896
magic-comma 2-10 3-1 55 [-10 -1, 5> 3,125 / 3,072 29.61356846

rectangular

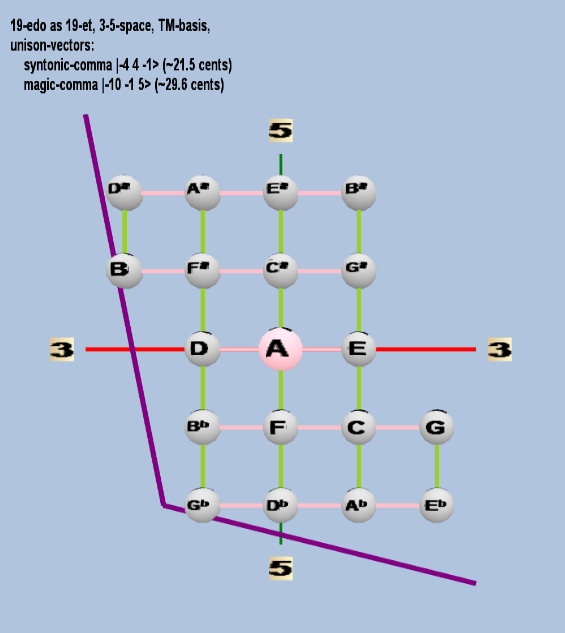
Lattice: 3,5-space, TM-basis, 19-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 19-edo, rectangular geometry, logarithmic 19-edo degree notation

triangular

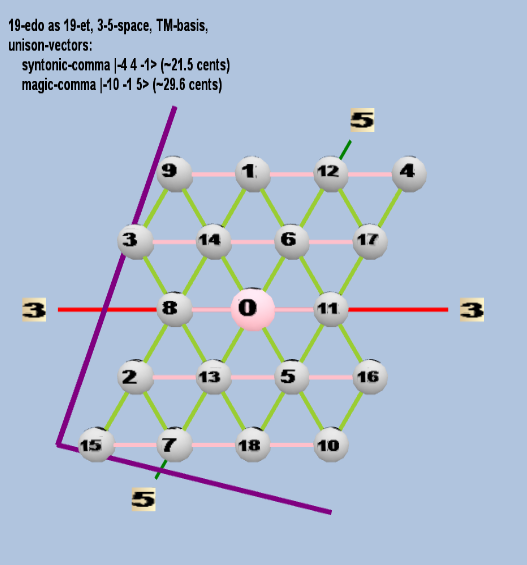
Lattice: 3,5-space, TM-basis, 19-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 19-edo, triangular geometry, logarithmic 19-edo degree notation

toroidal

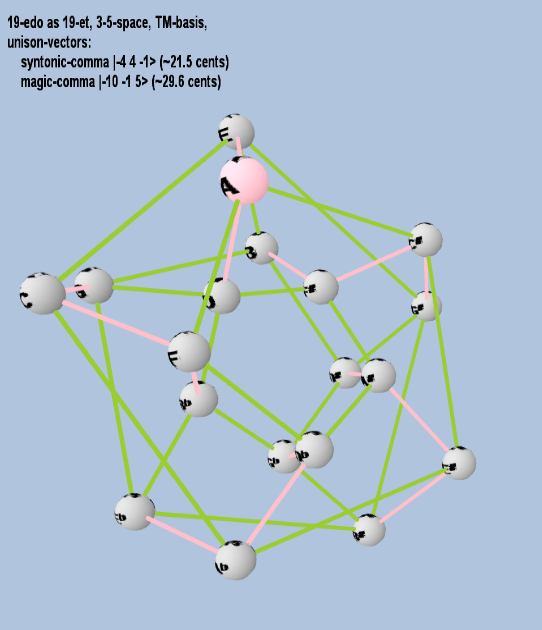
Lattice: 3,5-space, TM-basis, 19-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 19-edo, closed-curved torus geometry, logarithmic 19-edo degree notation

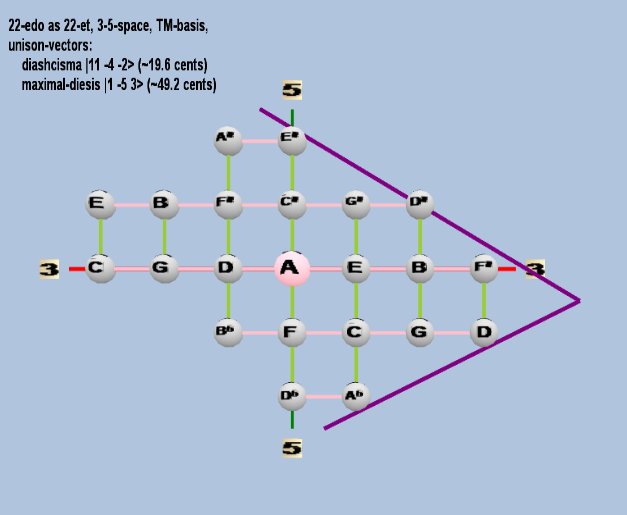
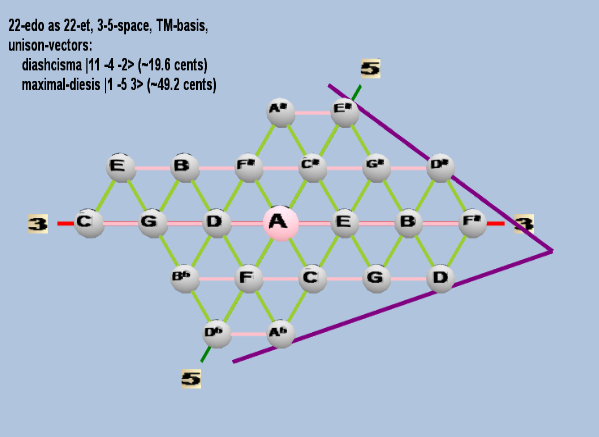
22 ET/EDO

name factors monzo ratio ~cents
diaschisma 211 3-4 5-2 [11 -4, -2> 2,048 / 2,025 19.55256881
maximal-diesis (porcupine-comma) 21 3-5 53 [ 1 -5, 3> 250 / 243 49.16613727

rectangular

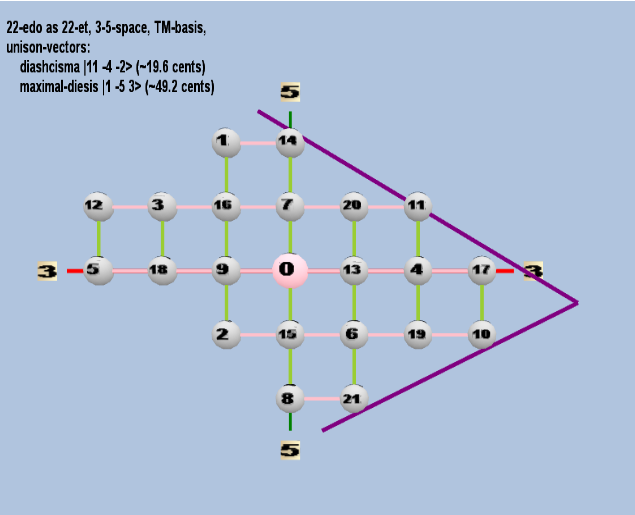
Lattice: 3,5-space, TM-basis, 22-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 22-edo, rectangular geometry, logarithmic 22-edo degree notation

triangular

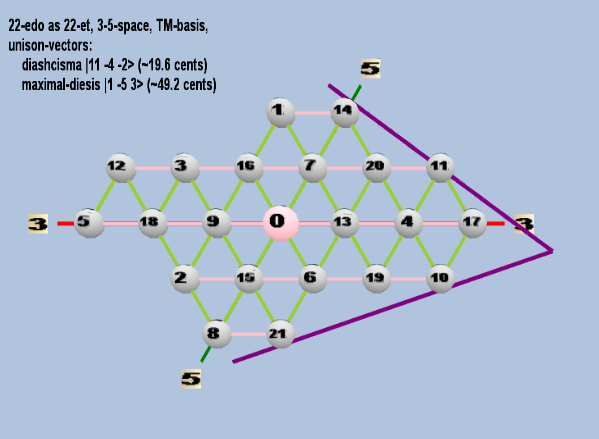
Lattice: 3,5-space, TM-basis, 22-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 22-edo, triangular geometry, logarithmic 22-edo degree notation

toroidal

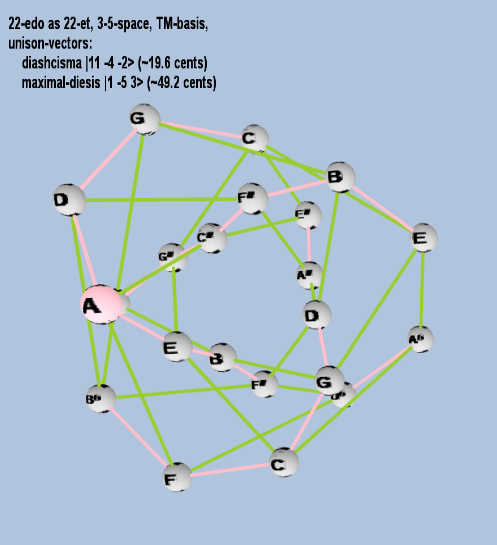
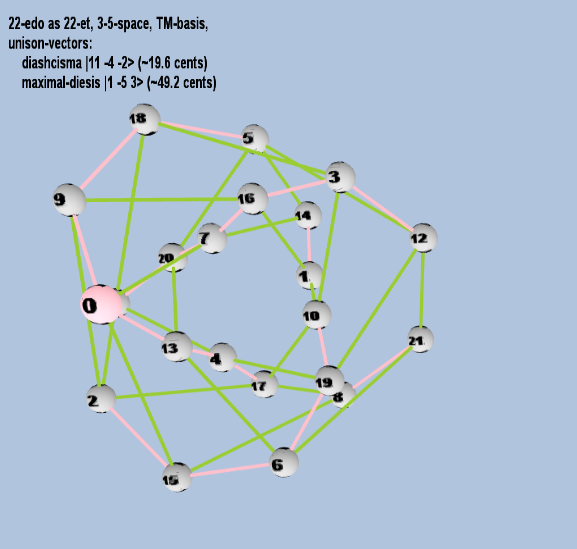
Lattice: 3,5-space, TM-basis, 22-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 22-edo, closed-curved torus geometry, logarithmic 22-edo degree notation

31 ET/EDO

name factors monzo ratio ~cents
würschmidt-comma 217 31 5-8 [17 1, -8> 393,216 / 390,625 11.44528995
syntonic-comma 2-4 34 5-1 [-4 4, -1> 81 / 80 21.5062896

rectangular

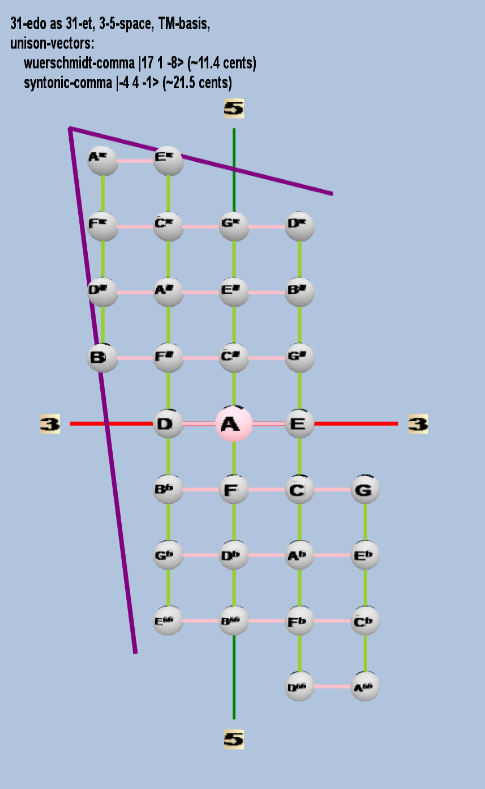
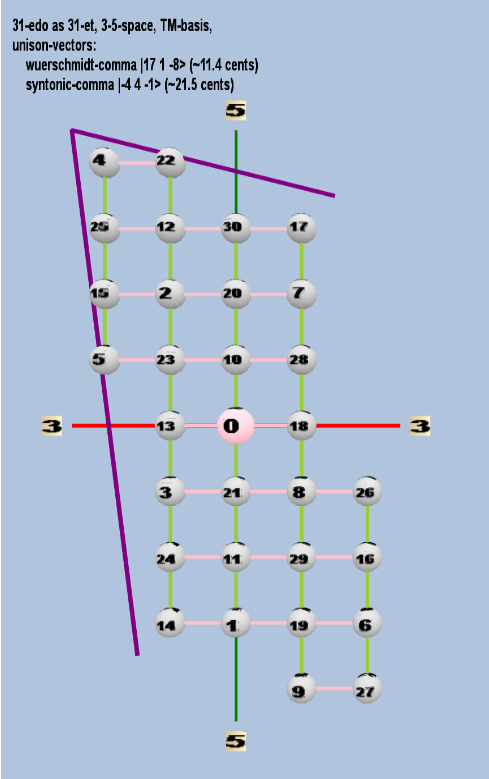
Lattice: 3,5-space, TM-basis, 31-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 31-edo, rectangular geometry, logarithmic 31-edo degree notation

triangular

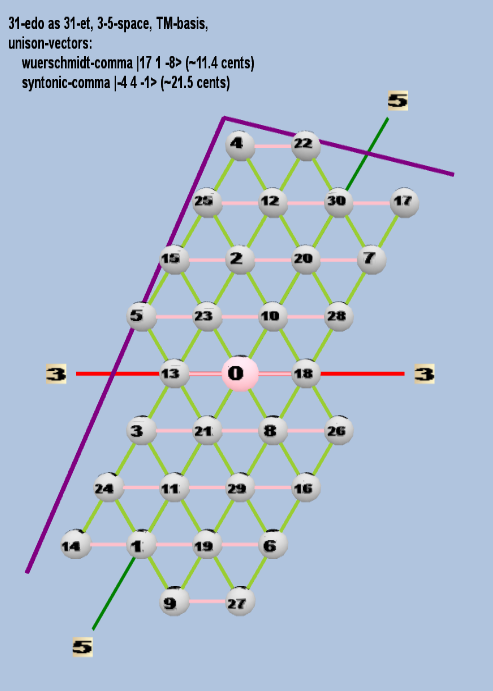
Lattice: 3,5-space, TM-basis, 31-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 31-edo, triangular geometry, logarithmic 31-edo degree notation

toroidal

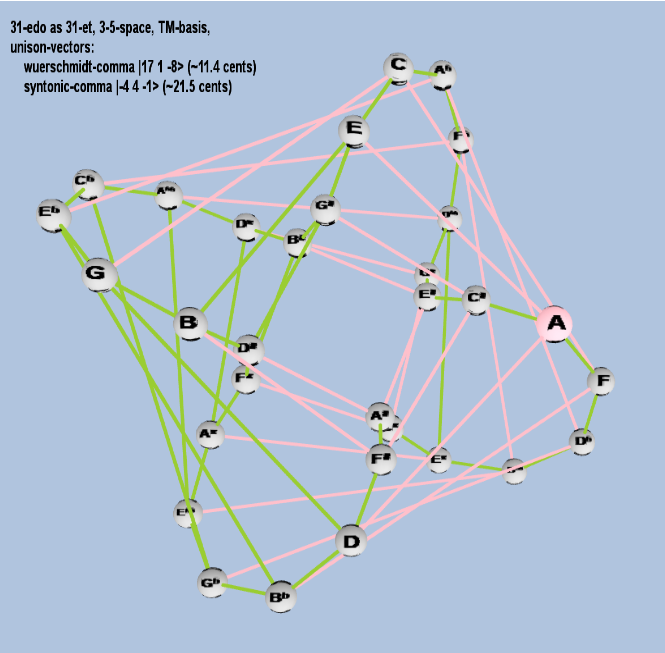
Lattice: 3,5-space, TM-basis, 31-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 31-edo, closed-curved torus geometry, logarithmic 31-edo degree notation

34 ET/EDO

name factors monzo ratio ~cents
kleisma 2-6 3-5 56 [-6 -5, 6> 15,625 / 15,552 8.107278862
diaschisma 211 3-4 5-2 [11 -4, -2> 2,048 / 2,025 19.55256881

rectangular

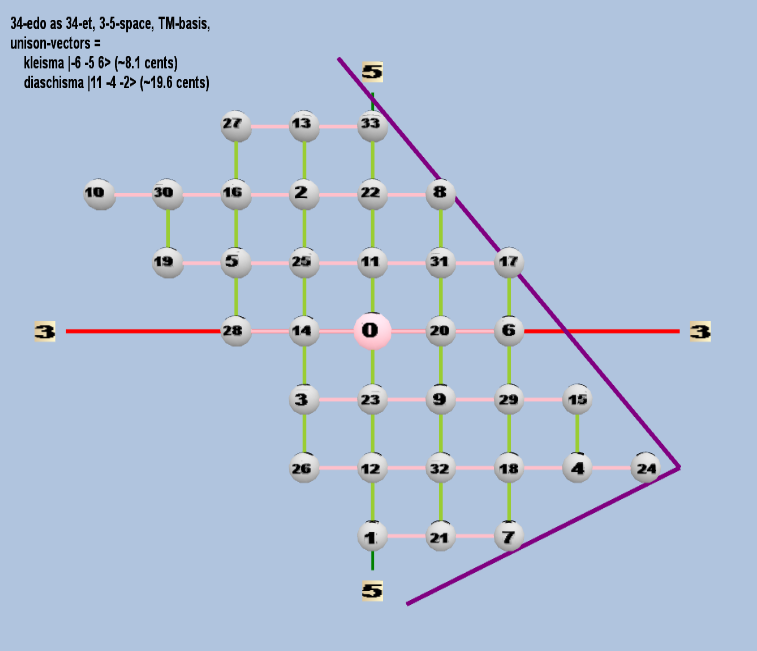
Lattice: 3,5-space, TM-basis, 34-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 34-edo, rectangular geometry, logarithmic 34-edo degree notation

triangular

Lattice: 3,5-space, TM-basis, 34-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 34-edo, triangular geometry, logarithmic 34-edo degree notation

toroidal

Lattice: 3,5-space, TM-basis, 34-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 34-edo, closed-curved torus geometry, logarithmic 34-edo degree notation

34 ET/EDO

name factors monzo ratio ~cents
minimal-diesis 25 3-9 54 [5 -9 4> 20,000 / 19,683 27.65984767085246
magic-comma 2-10 3-1 55 [-10 -1, 5> 3,125 / 3,072 29.61356846

rectangular

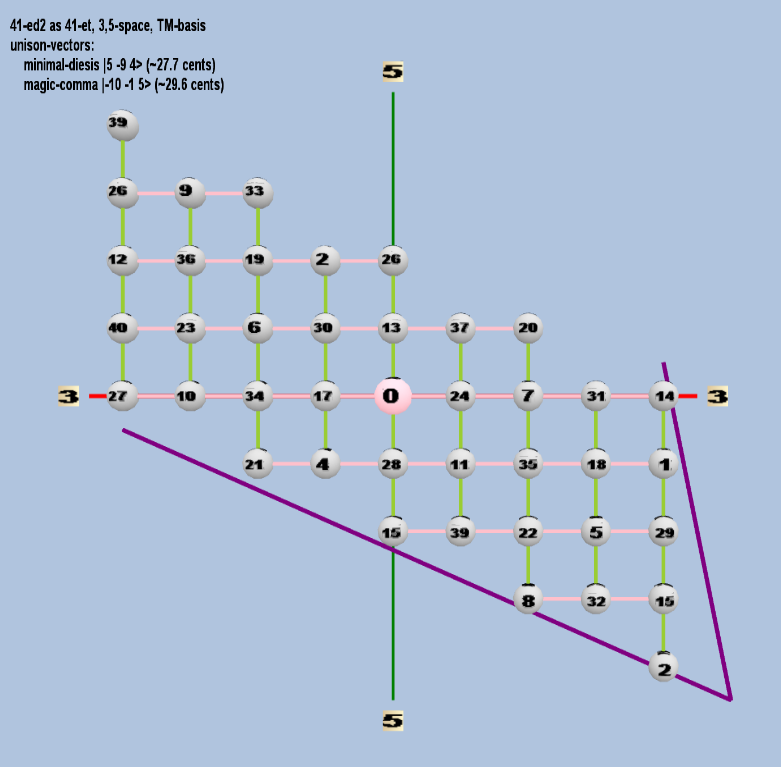
Lattice: 3,5-space, TM-basis, 41-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 41-edo, rectangular geometry, logarithmic 41-edo degree notation

triangular

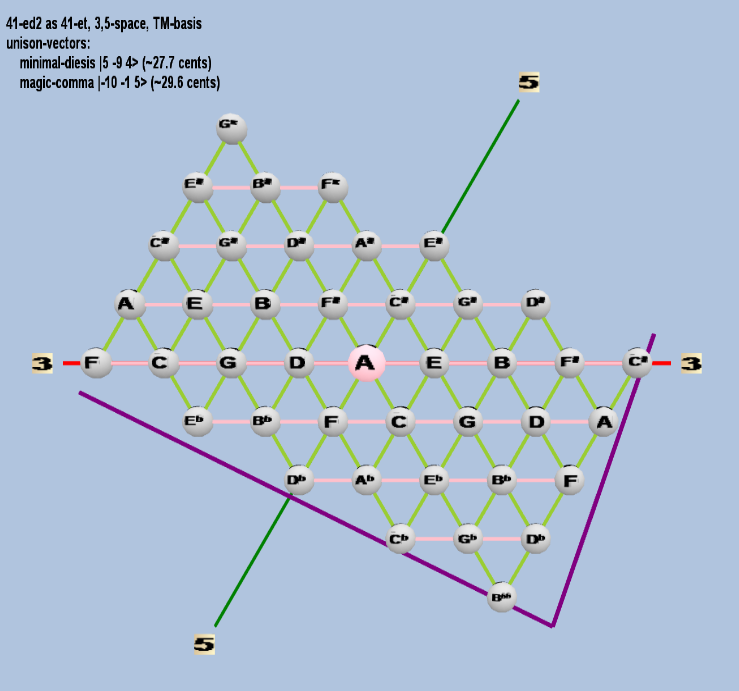
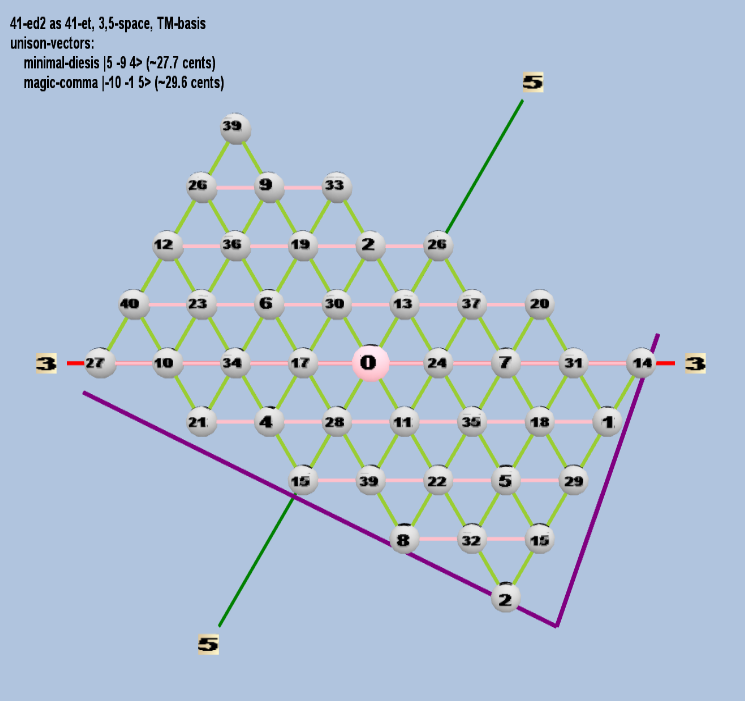
Lattice: 3,5-space, TM-basis, 41-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 41-edo, triangular geometry, logarithmic 41-edo degree notation

toroidal

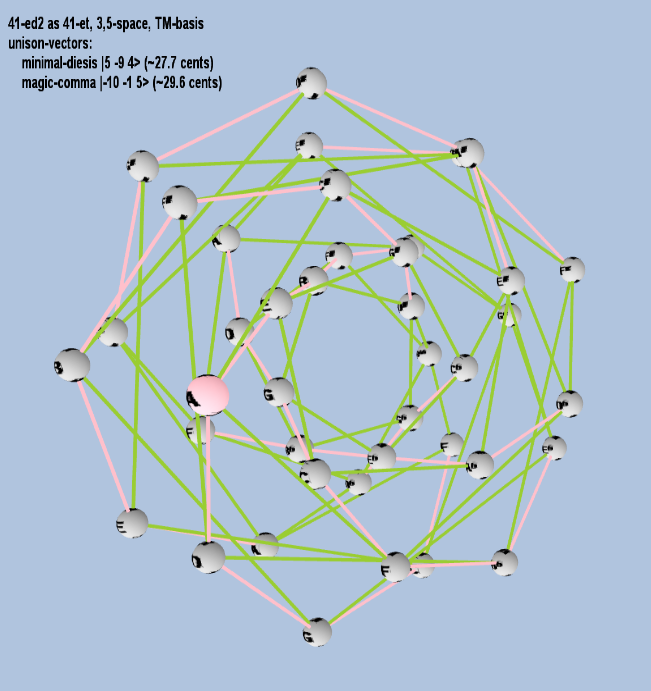
Lattice: 3,5-space, TM-basis, 41-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 41-edo, closed-curved torus geometry, logarithmic 41-edo degree notation

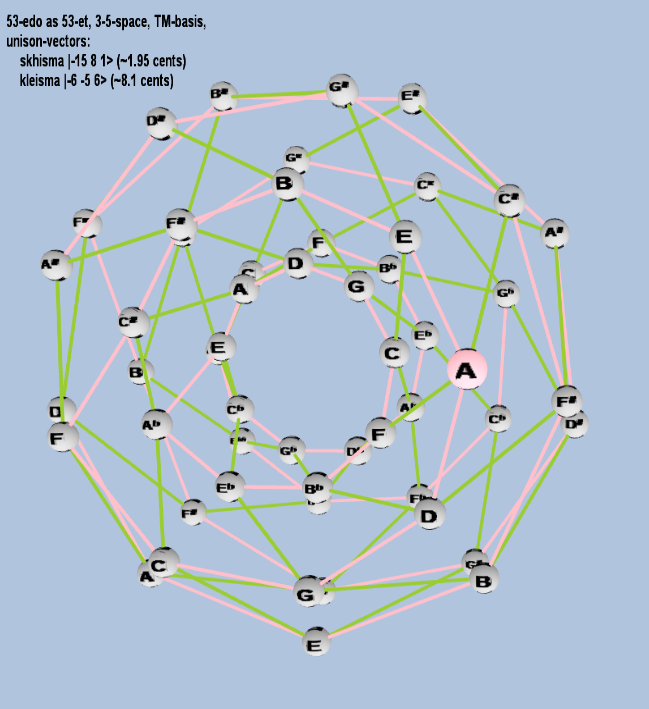
53 ET/EDO

name factors monzo ratio ~cents
skhisma 2-15 38 51 [-15, 8, 1> 32,805 / 32,768 1.953720788
kleisma 2-6 3-5 56 [-6 -5, 6> 15,625 / 15,552 8.107278862

rectangular

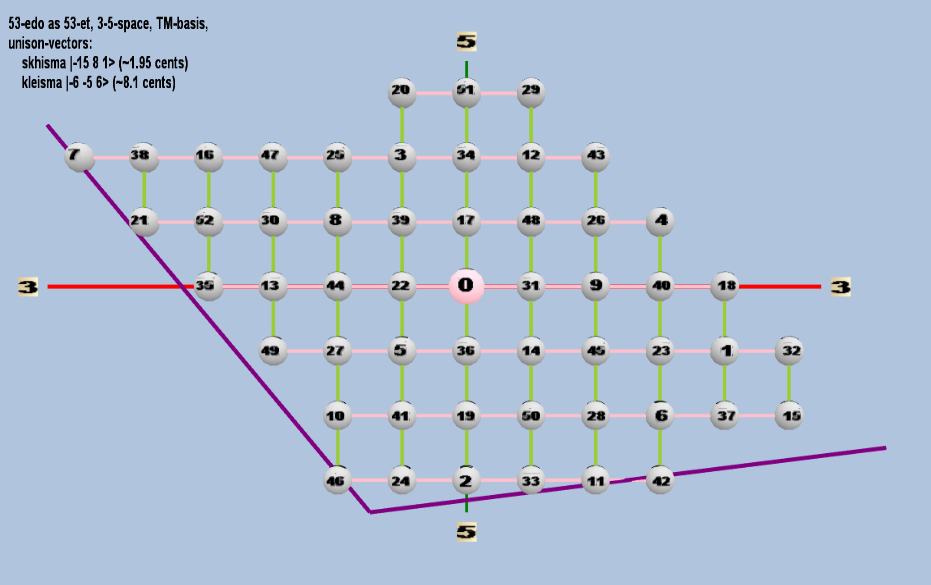
Lattice: 3,5-space, TM-basis, 53-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 53-edo, rectangular geometry, logarithmic 53-edo degree notation

triangular

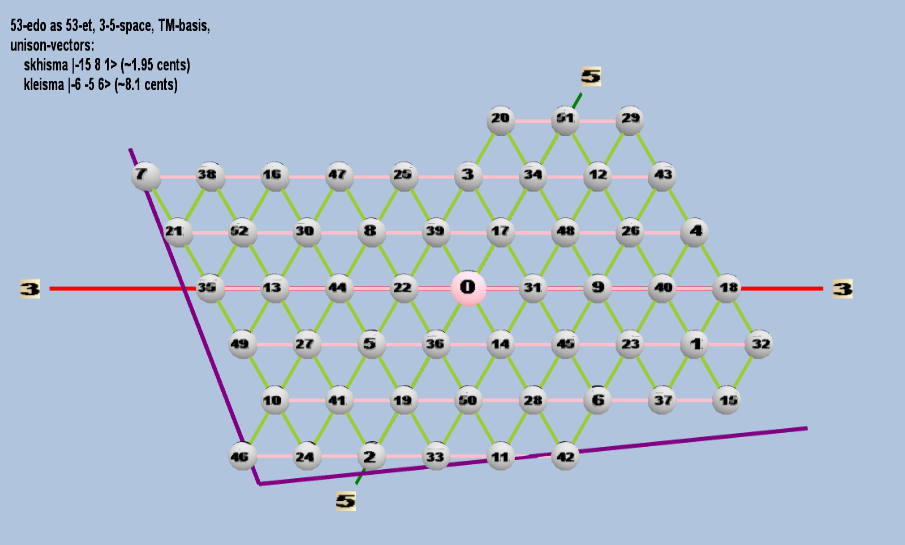
Lattice: 3,5-space, TM-basis, 53-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 53-edo, triangular geometry, logarithmic 53-edo degree notation

toroidal

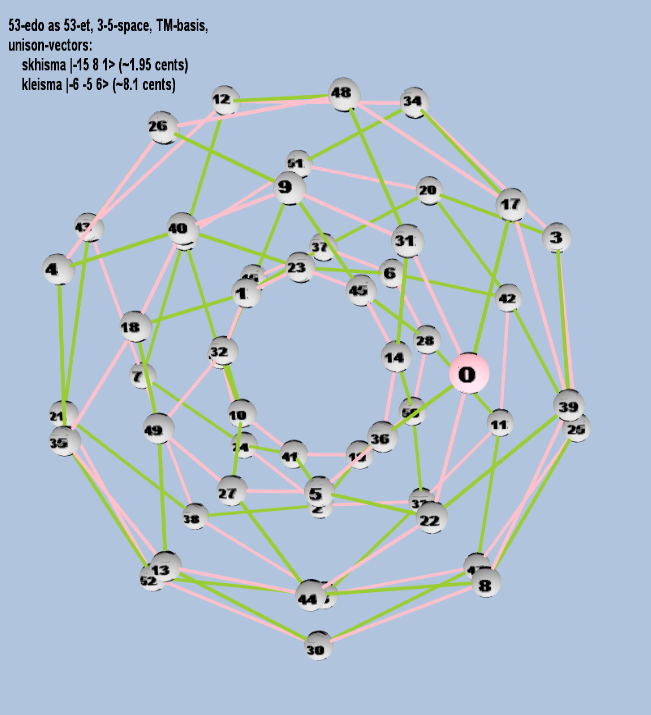
Lattice: 3,5-space, TM-basis, 53-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 53-edo, closed-curved torus geometry, logarithmic 53-edo degree notation

55 ET/EDO

name factors monzo ratio ~cents
syntonic-comma 2-4 34 5-1 [-4 4, -1> 81 / 80 21.5062896
(unnamed?) 227 35 5-15 [ 27, 5, -15> 32,614,907,904 / 30,517,578,125 115.069296354415

rectangular

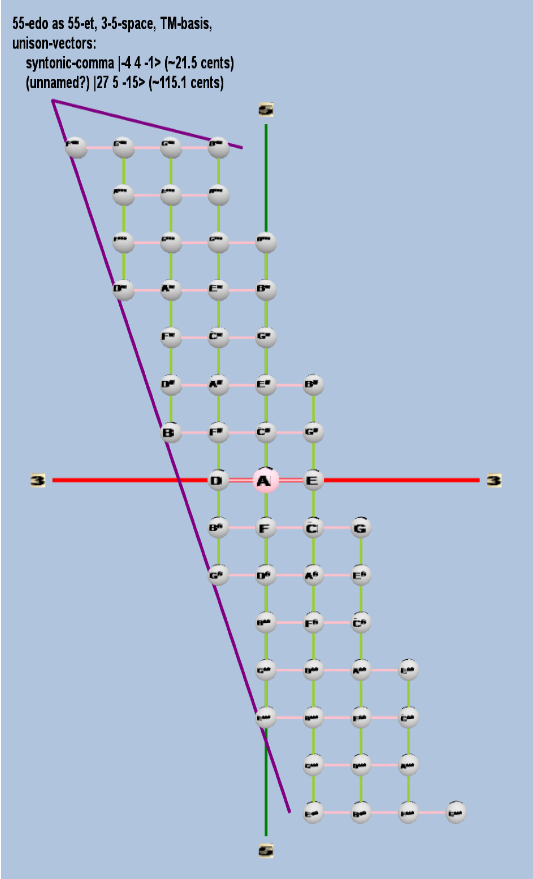
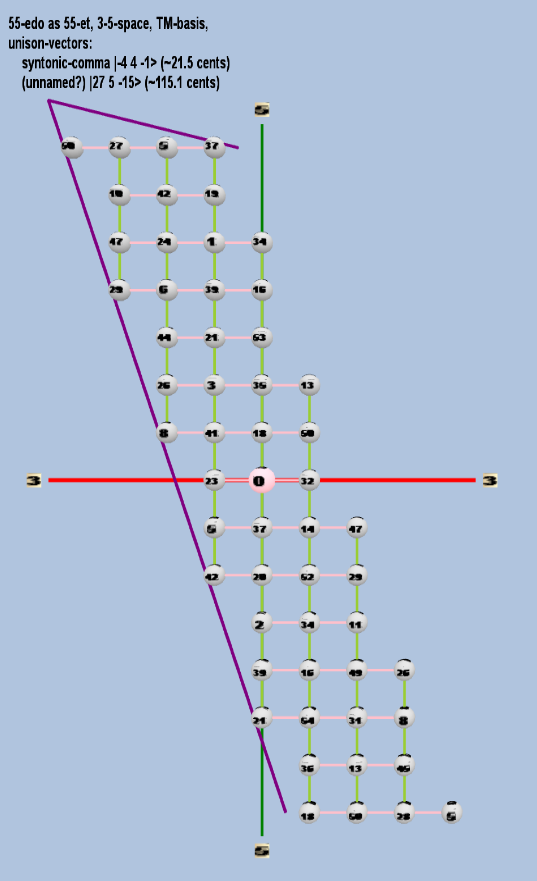
Lattice: 3,5-space, TM-basis, 55-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 55-edo, rectangular geometry, logarithmic 55-edo degree notation

triangular

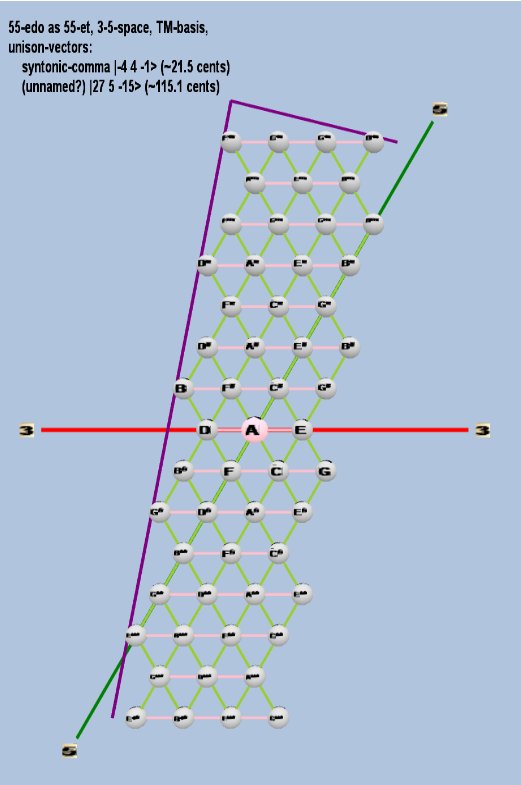
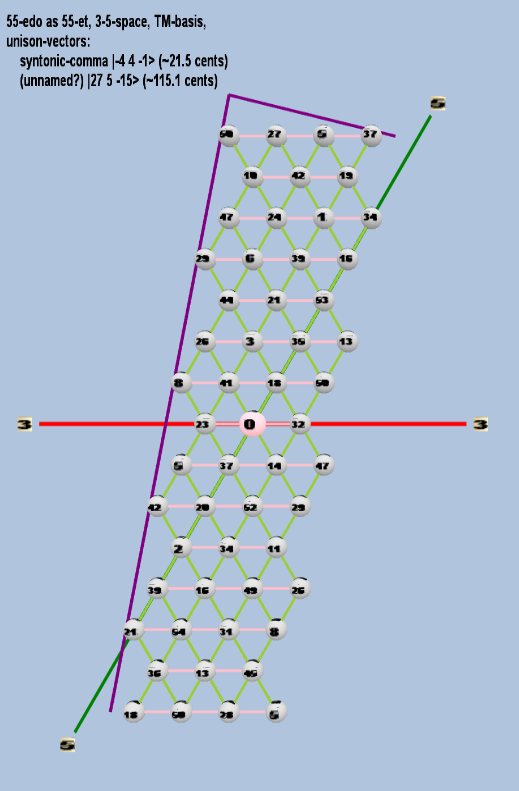
Lattice: 3,5-space, TM-basis, 55-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 55-edo, triangular geometry, logarithmic 55-edo degree notation

toroidal

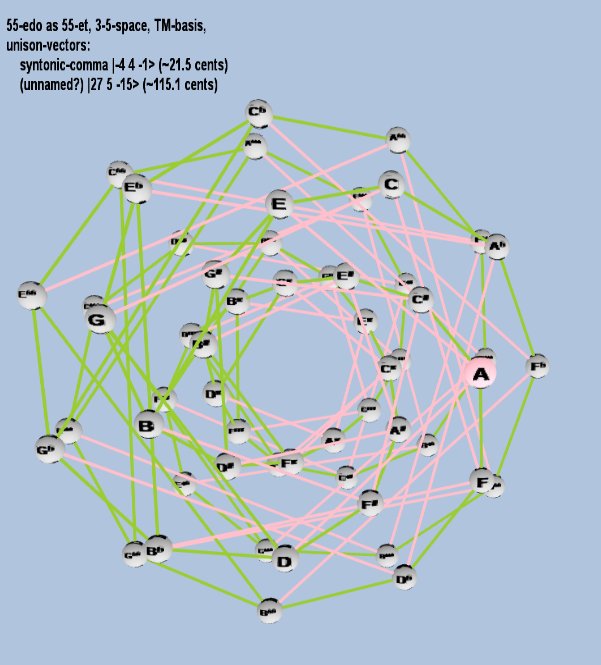
Lattice: 3,5-space, TM-basis, 55-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 55-edo, closed-curved torus geometry, logarithmic 55-edo degree notation

65 ET/EDO

name factors monzo ratio ~cents
skhisma 2-15 38 51 [-15, 8, 1> 32,805 / 32,768 1.953720788
sensipent-comma 22 39 5-7 [ 2, 9, -7> 78,732 / 78,125 13.39901073

rectangular

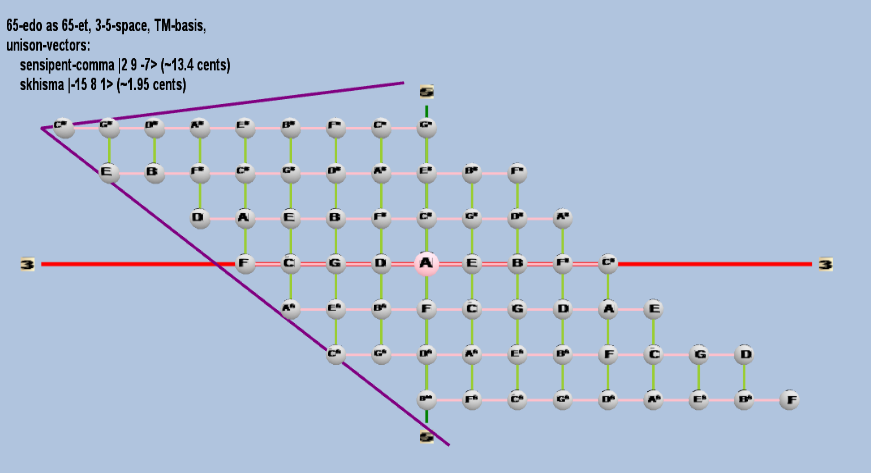
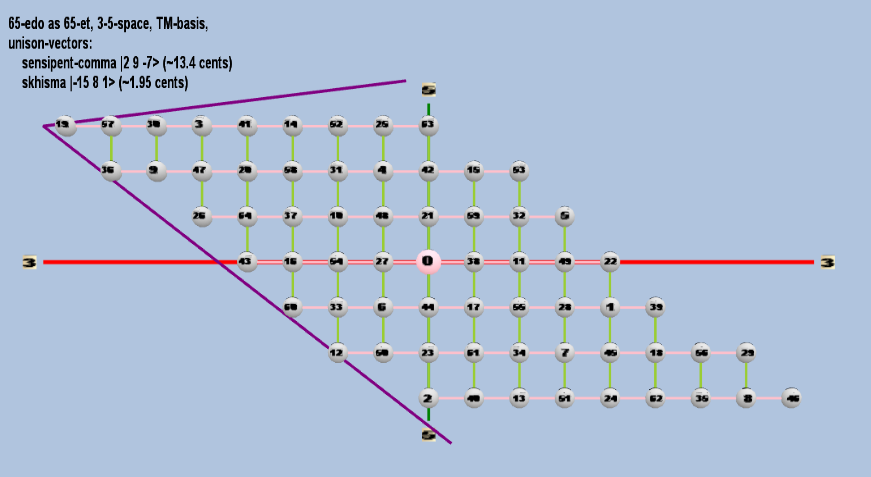
Lattice: 3,5-space, TM-basis, 65-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 65-edo, rectangular geometry, logarithmic 65-edo degree notation

triangular

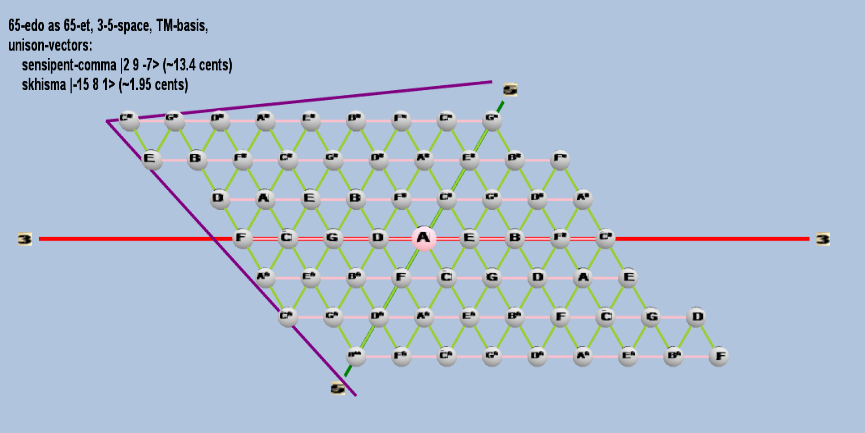
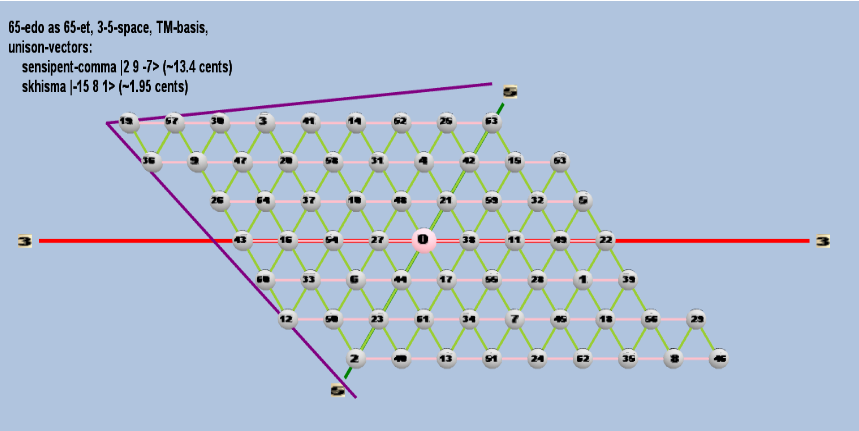
Lattice: 3,5-space, TM-basis, 65-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 65-edo, triangular geometry, logarithmic 65-edo degree notation

toroidal

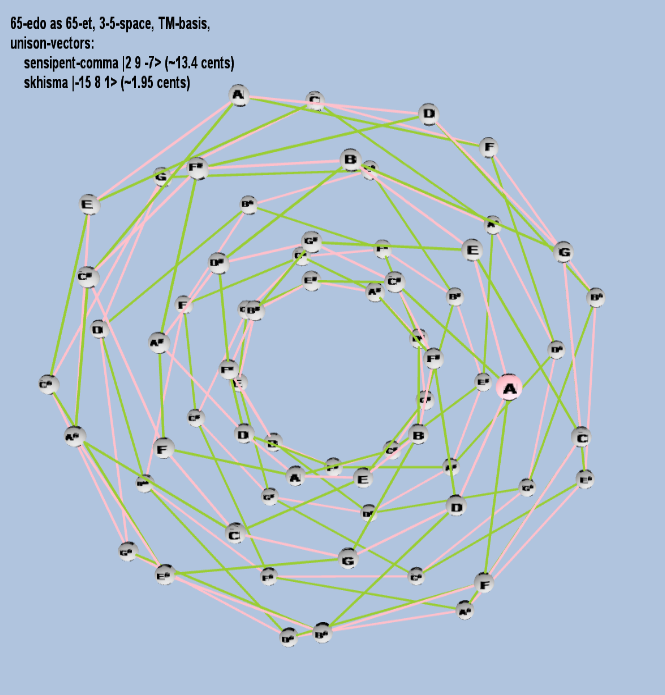
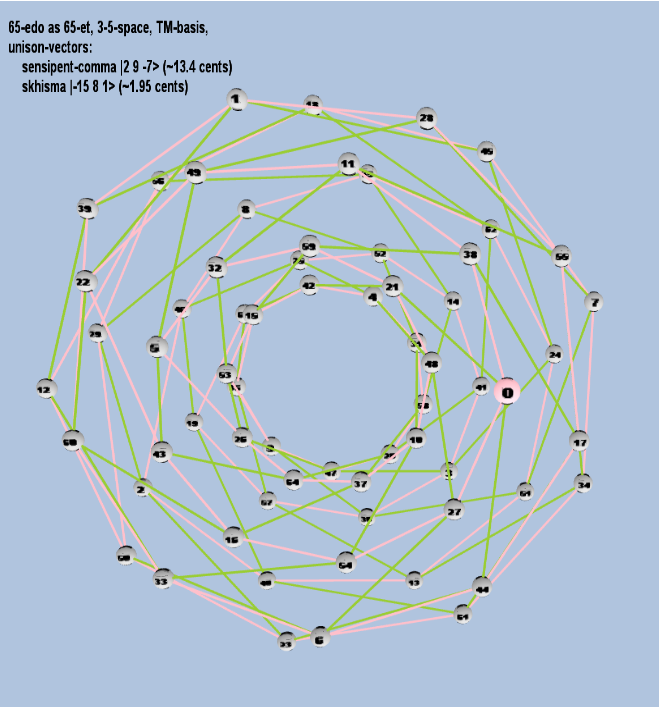
Lattice: 3,5-space, TM-basis, 65-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 65-edo, closed-curved torus geometry, logarithmic 65-edo degree notation

81 ET/EDO

name factors monzo ratio ~cents
majvam 240 37 5-22 [40, 7, -22> 2,404,631,929,946,112 / 2,384,185,791,015,625 14.78330103134586
syntonic-comma 2-4 34 5-1 [-4 4, -1> 81 / 80 21.5062896

rectangular

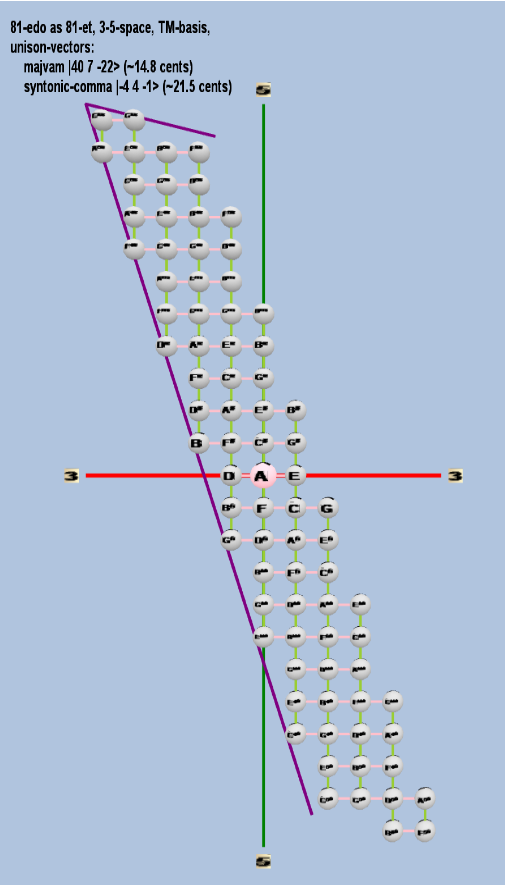
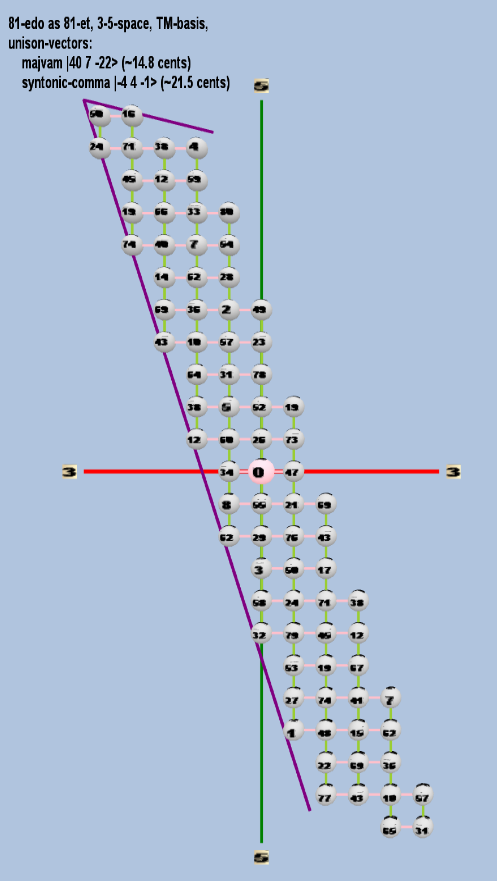
Lattice: 3,5-space, TM-basis, 81-edo, rectangular geometry, letter notation Lattice: 3,5-space, TM-basis, 81-edo, rectangular geometry, logarithmic 81-edo degree notation

triangular

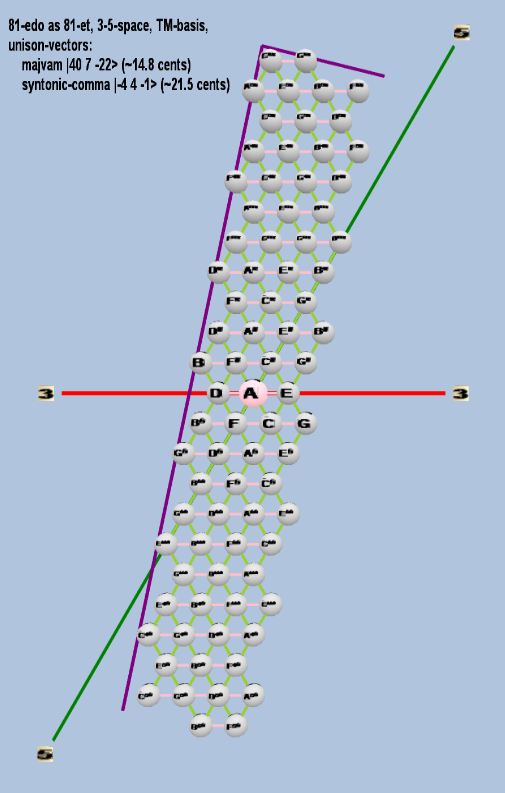
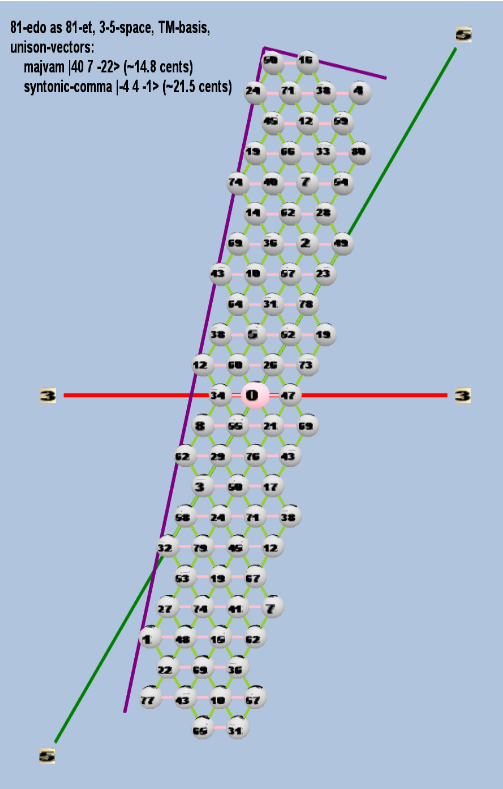
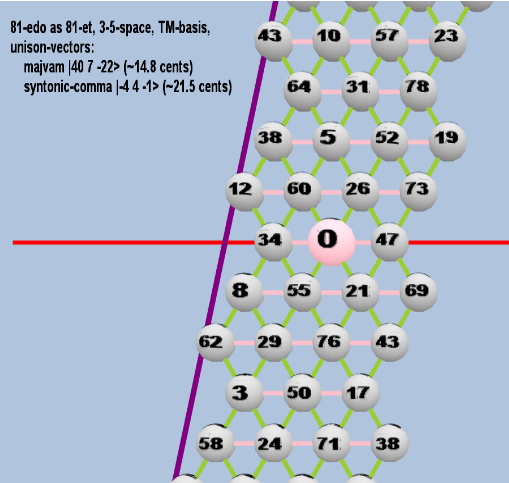
Lattice: 3,5-space, TM-basis, 81-edo, triangular geometry, letter notation Lattice: 3,5-space, TM-basis, 81-edo, triangular geometry, logarithmic 81-edo degree notation Lattice: 3,5-space, TM-basis, 81-edo, triangular geometry, logarithmic 81-edo degree notation, zoom-in of central region

toroidal

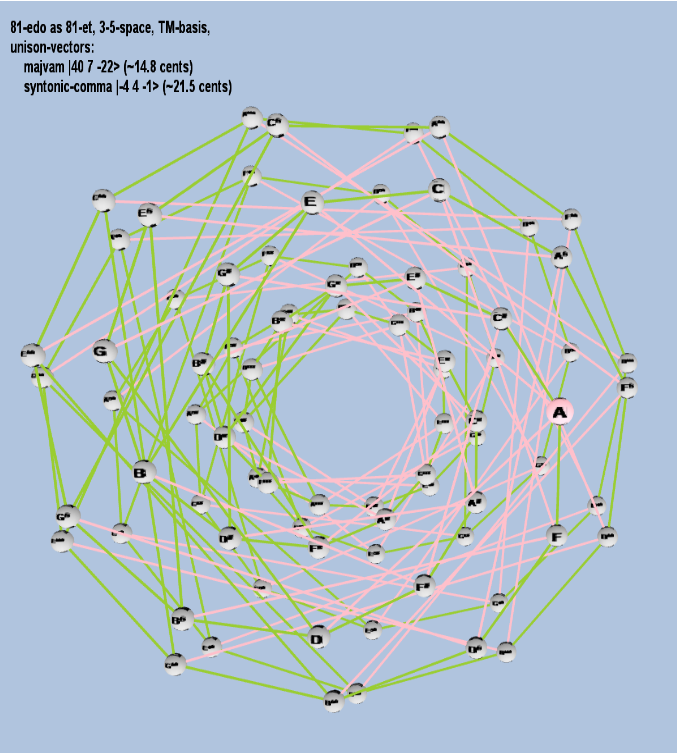
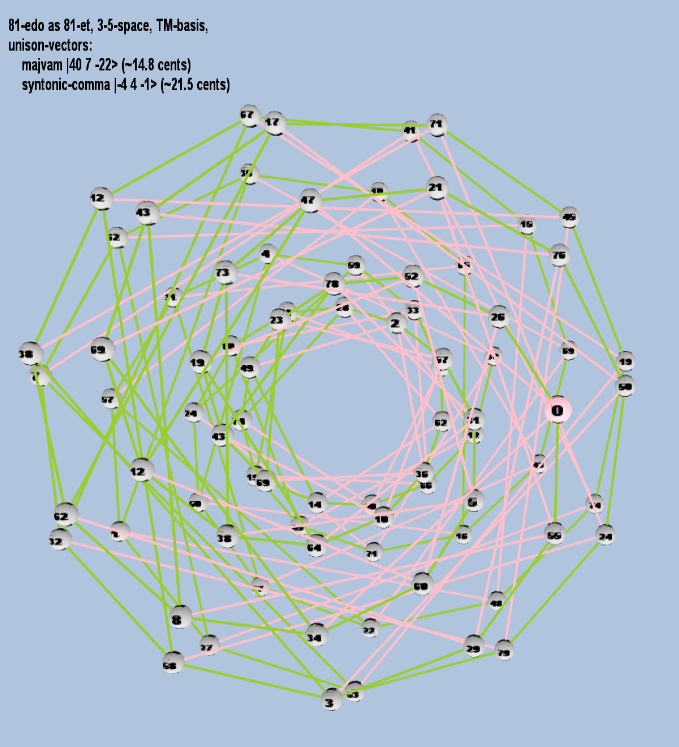
Lattice: 3,5-space, TM-basis, 81-edo, closed-curved torus geometry, letter notation Lattice: 3,5-space, TM-basis, 81-edo, closed-curved torus geometry, logarithmic 81-edo degree notation

For purposes of illustrating the lattice bases, the letter notation is largely irrelevant for cardinalities larger than 81-ed2, so all subsequent lattices will show notation only in the logarithmic ED2 degrees.

118 ET/EDO

name factors monzo ratio ~cents
skhisma 2-15 38 51 [-15, 8, 1> 32,805 / 32,768 1.953720788
parakleisma 28 314 5-13 [ 8, 14, -13> 1,224,440,064 / 1,220,703,125 5.291731873

rectangular

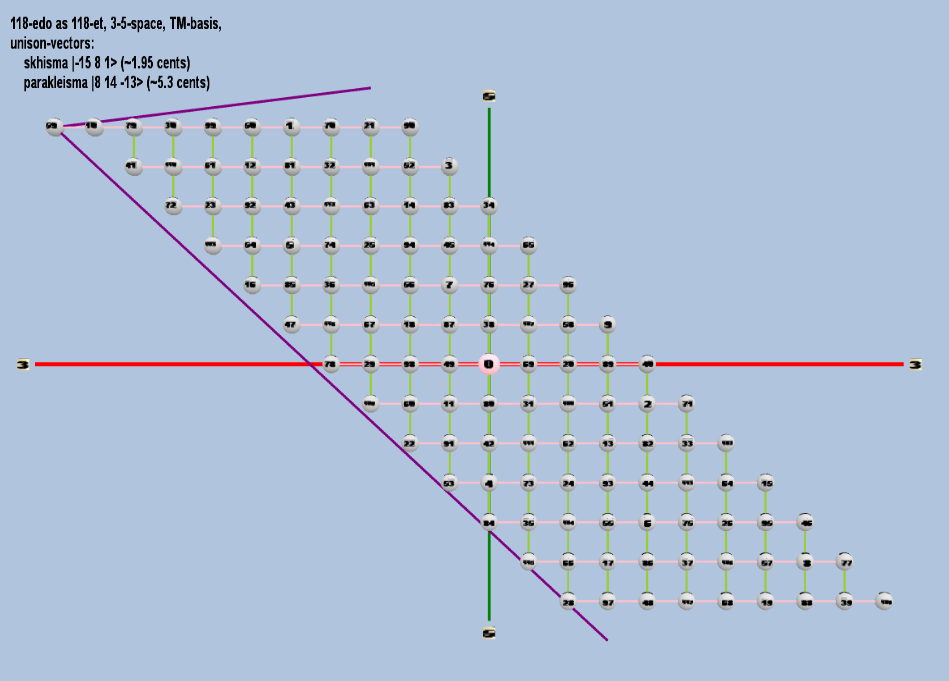
Lattice: 3,5-space, TM-basis, 118-edo, rectangular geometry, logarithmic 118-edo degree notation

toroidal

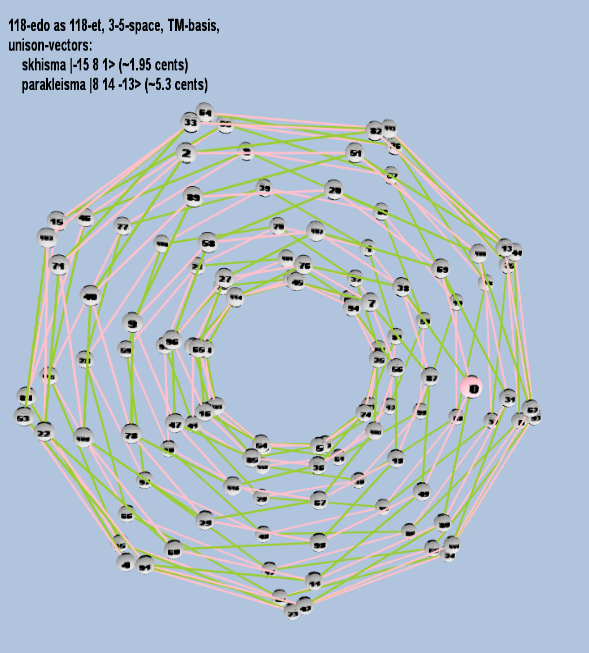
Lattice: 3,5-space, TM-basis, 118-edo, closed-curved torus geometry, logarithmic 118-edo degree notation

171 ET/EDO

name factors monzo ratio ~cents
skhisma 2-15 38 51 [-15, 8, 1> 32,805 / 32,768 1.953720788
19-tone-comma 2-14 3-19 519 [ -14, -19, 19> 19,073,486,328,125 / 19,042,491,875,328 2.8155469895004357

rectangular

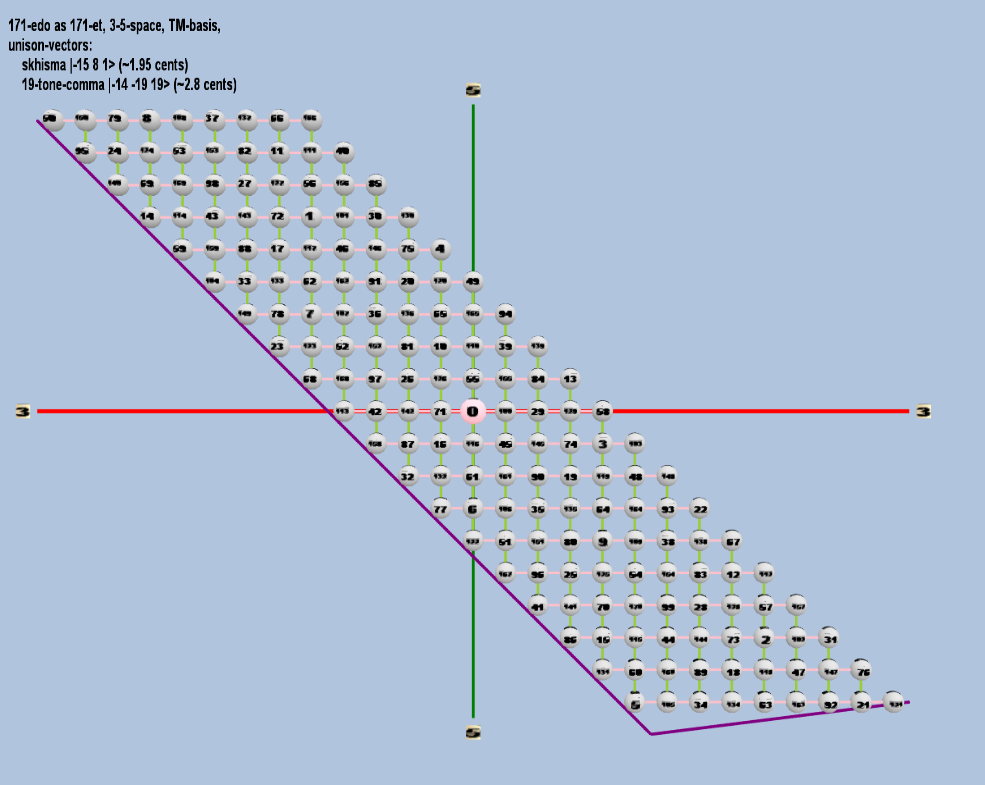
Lattice: 3,5-space, TM-basis, 171-edo, rectangular geometry, logarithmic 171-edo degree notation

toroidal

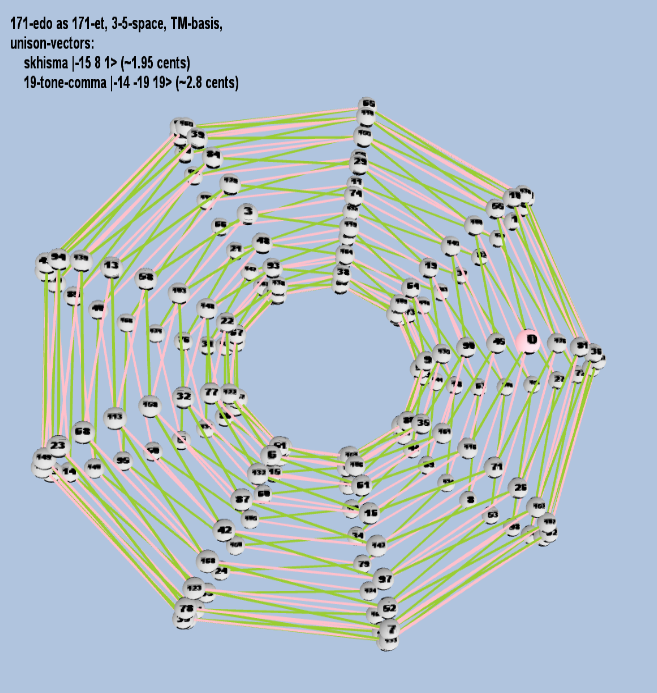
Lattice: 3,5-space, TM-basis, 171-edo, closed-curved torus geometry, logarithmic 171-edo degree notation

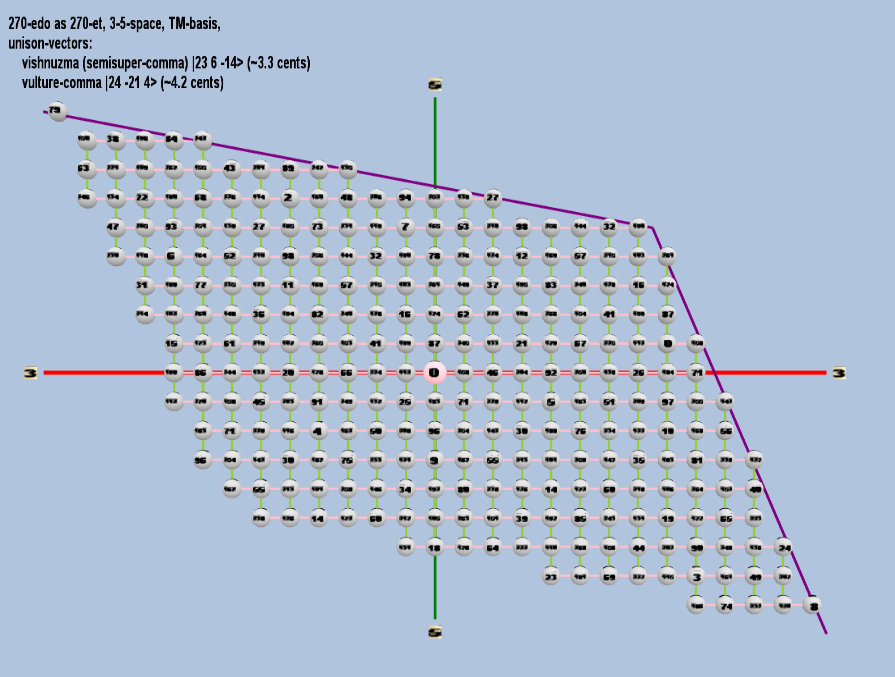
270 ET/EDO

name factors monzo ratio ~cents
vishnuzma (semisuper-comma) 223 36 5-14 [ 23, 6, -14> 6,115,295,232 / 6,103,515,625 3.3380110846370235
vulture-comma 224 3-21 54 [24, -21, 4> 10,485,760,000 / 10,460,353,203 4.199837286203549

rectangular

Lattice: 3,5-space, TM-basis, 270-edo, rectangular geometry, logarithmic 270-edo degree notation

Because of its immense usefulness as a simpler integer replacement for cents, the central portion of the rectangular lattice is also shown in a zoom-in view so that the logarithmic degree notation can be easily read for the ratios closest to 1/1 (n^0).

rectangular: zoom-in of central portion

Lattice: 3,5-space, TM-basis, 270-edo, rectangular geometry, logarithmic 270-edo degree notation

toroidal

Lattice: 3,5-space, TM-basis, 270-edo, closed-curved torus geometry, logarithmic 270-edo degree notation

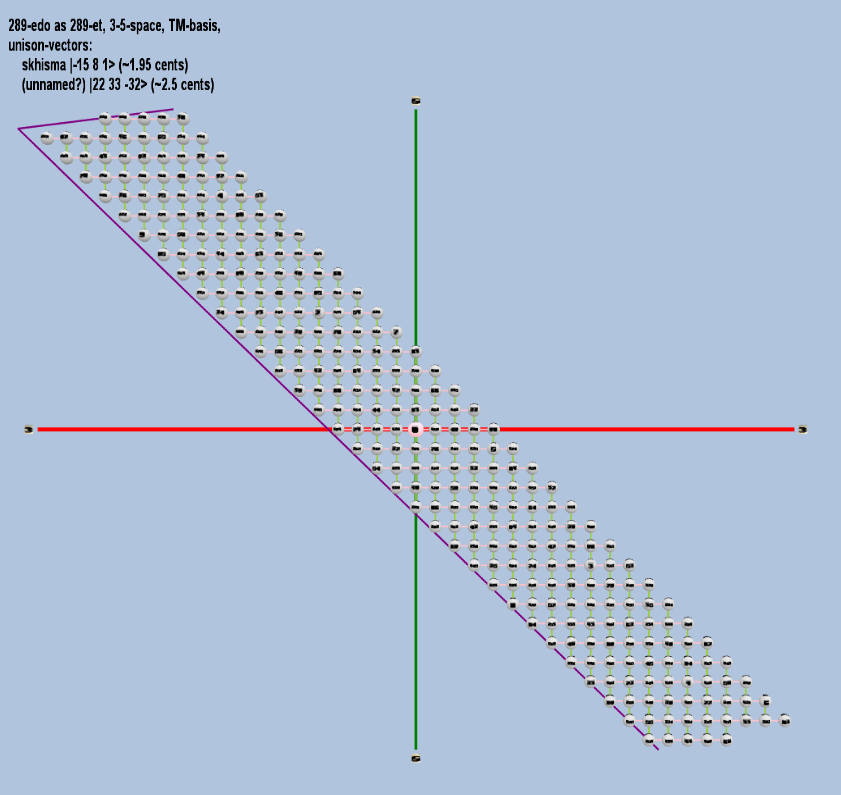
289 ET/EDO

name factors monzo ratio ~cents
(unnamed?) 222 333 5-32 [ 22 33, -32> 23,316,389,970,546,096,340,992 / 23,283,064,365,386,962,890,625 2.4761848830704634
skhisma 2-15 38 51 [-15, 8, 1> 32,805 / 32,768 1.953720788

rectangular

Lattice: 3,5-space, TM-basis, 289-edo, rectangular geometry, logarithmic 289-edo degree notation

toroidal

Lattice: 3,5-space, TM-basis, 289-edo, closed-curved torus geometry, logarithmic 289-edo degree notation

Below is an angled view of the 289-et torus, simply to show the beauty of the spiral formations.

Lattice: 3,5-space, TM-basis, 289-edo, closed-curved torus geometry, logarithmic 289-edo degree notation

441 ET/EDO

name factors monzo ratio ~cents
ennealimma 21 3-27 518 [ 1, -27, 18> 7,629,394,531,250 / 7,625,597,484,987 0.861826202
lunama (hemithirds-comma) 238 3-2 5-15 [38, -2, -15> 274,877,906,944 / 274,658,203,125 1.384290297

559 ET/EDO

name factors monzo ratio ~cents
lunama (hemithirds-comma) 238 3-2 5-15 [38, -2, -15> 274,877,906,944 / 274,658,203,125 1.384290297
minortonic-comma 2-16 335 5-17 [-16, 35, -17> 50,031,545,098,999,707 / 50,000,000,000,000,000 1.091894586

612 ET/EDO

name factors monzo ratio ~cents
kwazy 2-53 310 516 [-53, 10, 16> 9,010,162,353,515,625 / 9,007,199,254,740,992 0.569430491
ennealimma 21 3-27 518 [ 1, -27, 18> 7,629,394,531,250 / 7,625,597,484,987 0.861826202

rectangular

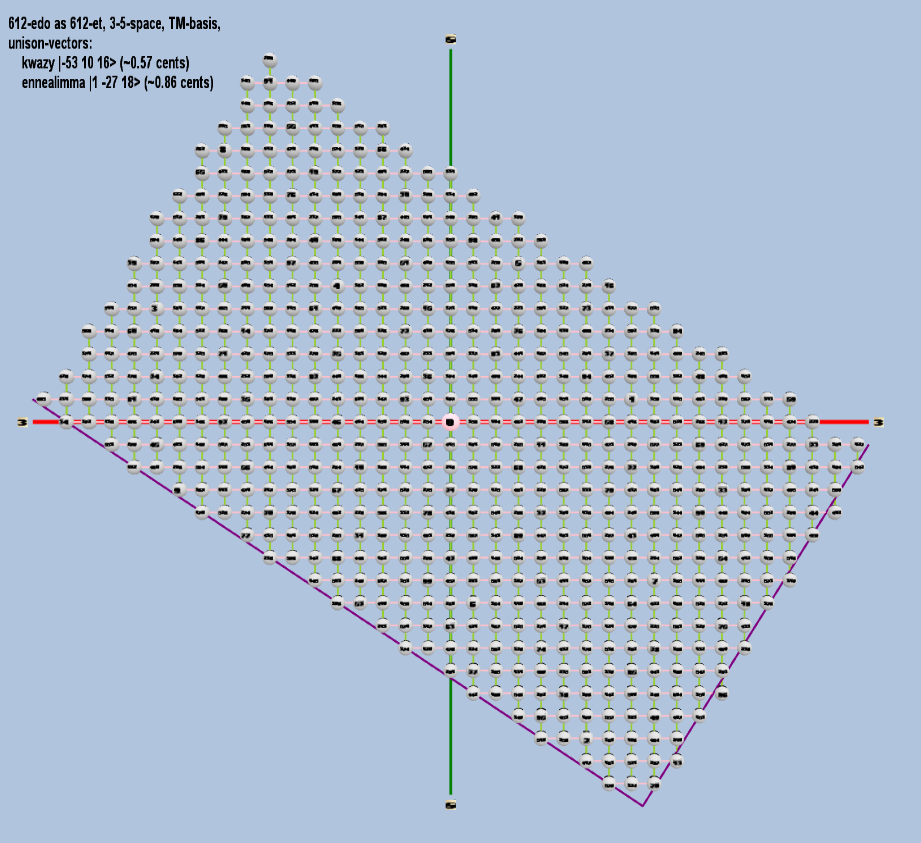
Lattice: 3,5-space, TM-basis, 612-edo, rectangular geometry, logarithmic 612-edo degree notation

toroidal top view

Lattice: 3,5-space, TM-basis, 612-edo, rectangular geometry, logarithmic 612-edo degree notation

toroidal close up

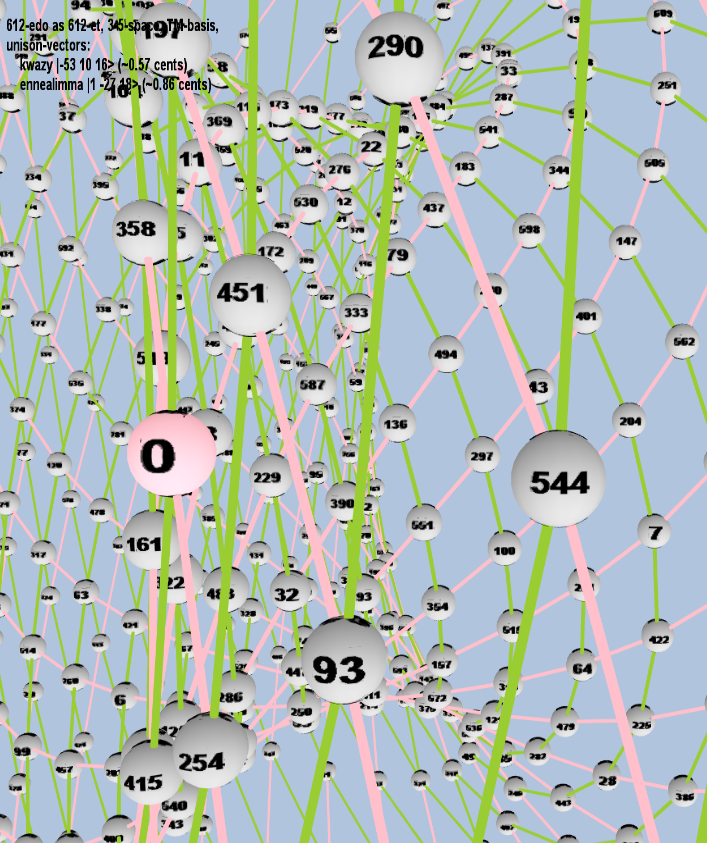
Lattice: 3,5-space, TM-basis, 612-edo, closed-curved torus geometry, logarithmic 612-edo degree notation

toroidal side-view

Lattice: 3,5-space, TM-basis, 612-edo, closed-curved torus geometry, logarithmic 612-edo degree notation

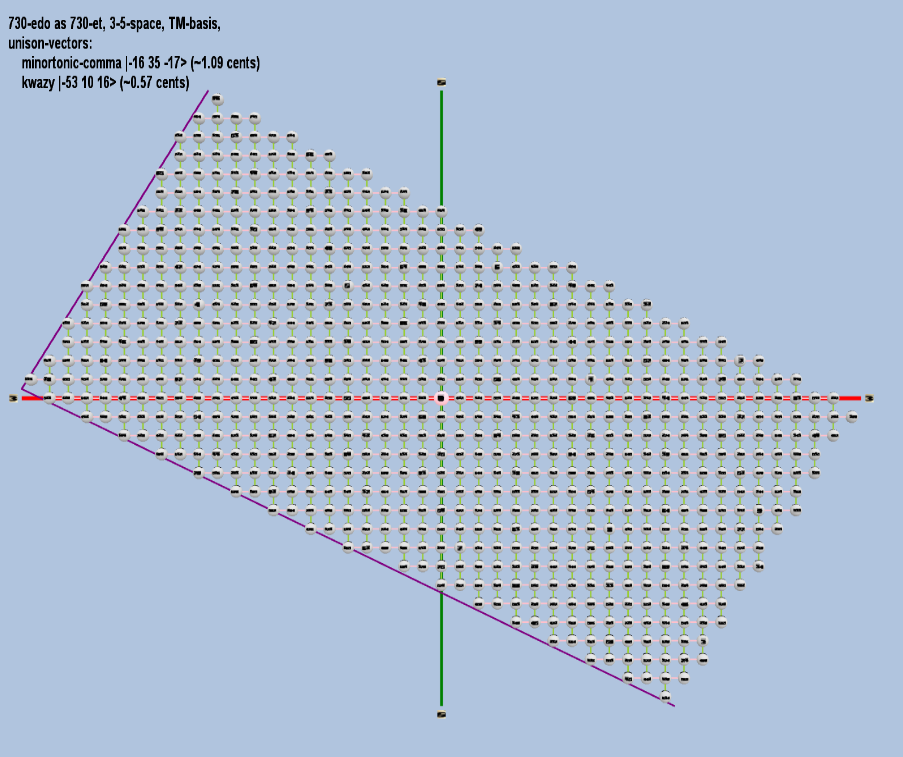
730 ET/EDO

name factors monzo ratio ~cents
minortonic-comma 2-16 335 5-17 [-16, 35, -17> 50,031,545,098,999,707 / 50,000,000,000,000,000 1.091894586
kwazy 2-53 310 516 [-53, 10, 16> 9,010,162,353,515,625 / 9,007,199,254,740,992 0.569430491

rectangular

Lattice: 3,5-space, TM-basis, 730-edo, rectangular geometry, logarithmic 730-edo degree notation

Because of its importance as a simpler integer replacement for cents in Woolhouse 1835, the central portion of the rectangular lattice is also shown in a zoom-in view so that the logarithmic degree notation can be easily read for the ratios closest to 1/1 (n^0).

rectangular: zoom-in of central portion

Lattice: 3,5-space, TM-basis, 730-edo, rectangular geometry, logarithmic 730-edo degree notation

toroidal

Lattice: 3,5-space, TM-basis, 730-edo, closed-curved torus geometry, logarithmic 730-edo degree notation

When the cardinality of the EDO gets this high, it is difficult to see a difference in the geometry of their toruses, so graphics for the following are omitted. In addition, ratios are omitted from the list of unison-vectors, because of the size of the numbers in their numerators and denominators, with only the factors shown.

1,171 ET/EDO and Above

additional 5-limit lattice bases
1,171 ET / EDO 237 325 5-33 254 32 5-37
1,783 ET / EDO 254 32 5-37 2-90 3-15 549
2,513 ET / EDO 2-107 347 514 2-17 362 5-35
4,296 ET / EDO 271 337 5-99 2-90 3-15 549
6,809 ET / EDO 2-178 3146 523 2-90 3-15 549
16,572 ET / EDO 292 3191 5-170 2161 3-81 5-12
20,868 ET / EDO 2161 3-81 5-12 221 3290 5-207
25,164 ET / EDO 2-111 3-305 5256 2161 3-81 5-12
52,841 ET / EDO 221 3290 5-207 2-412 3153 573
73,709 ET / EDO 221 3290 5-207 2-573 3237 585
78,005 ET / EDO 2140 3195 5-374 2-573 3237 585

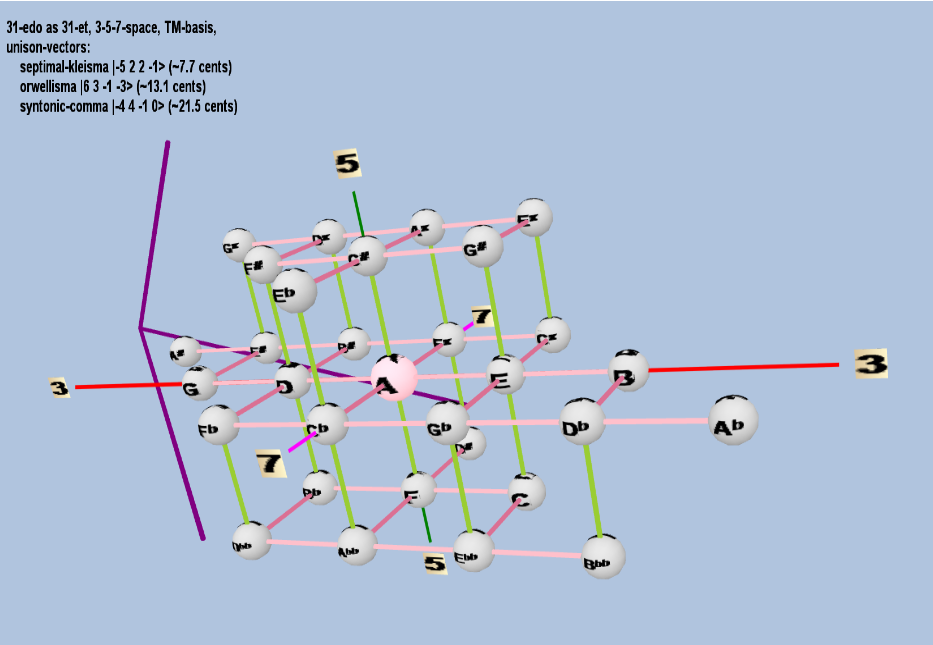
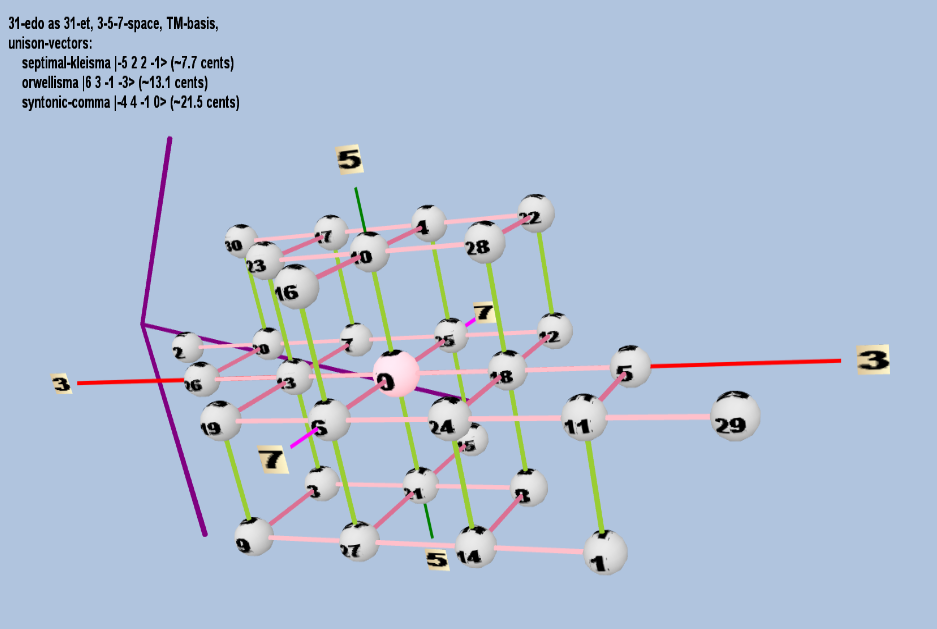
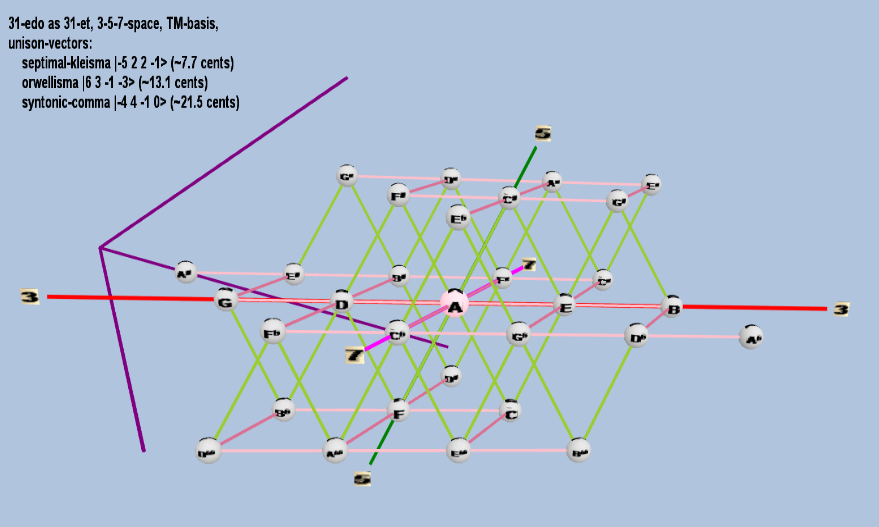
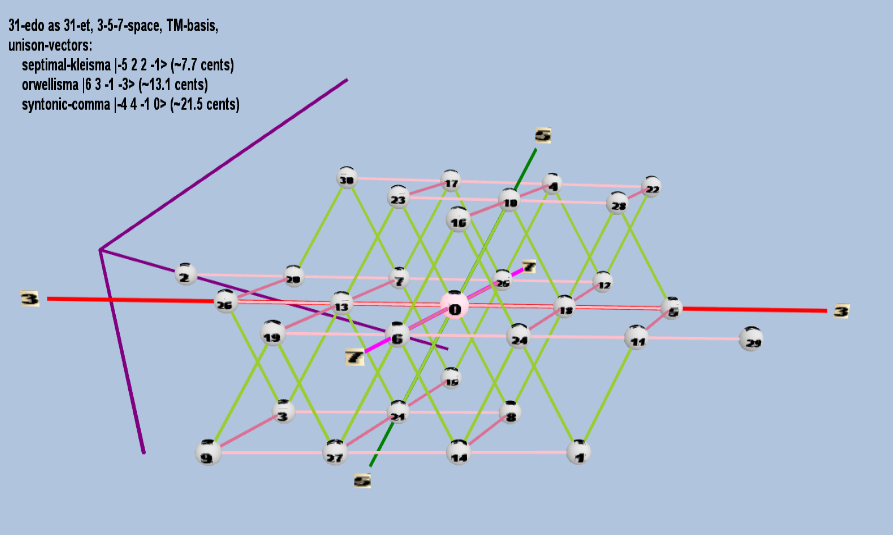
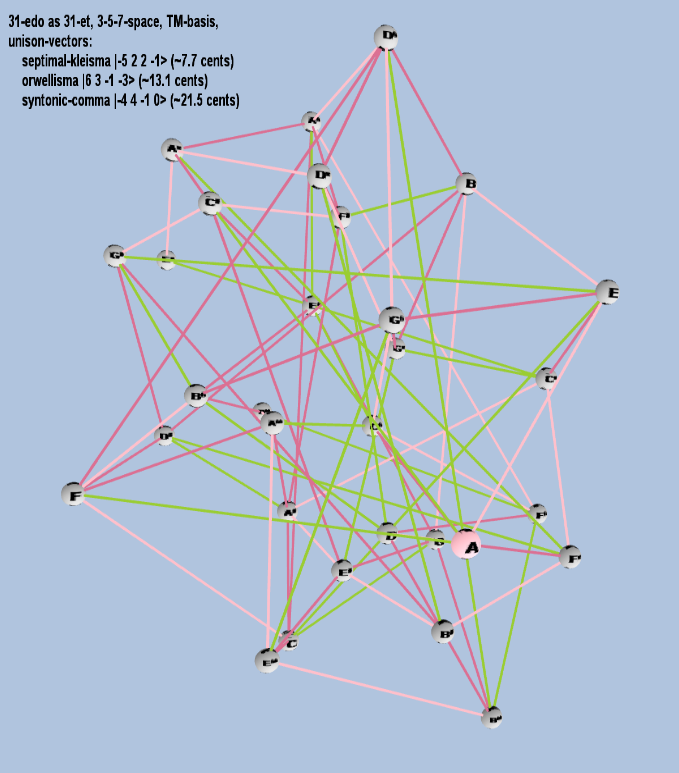
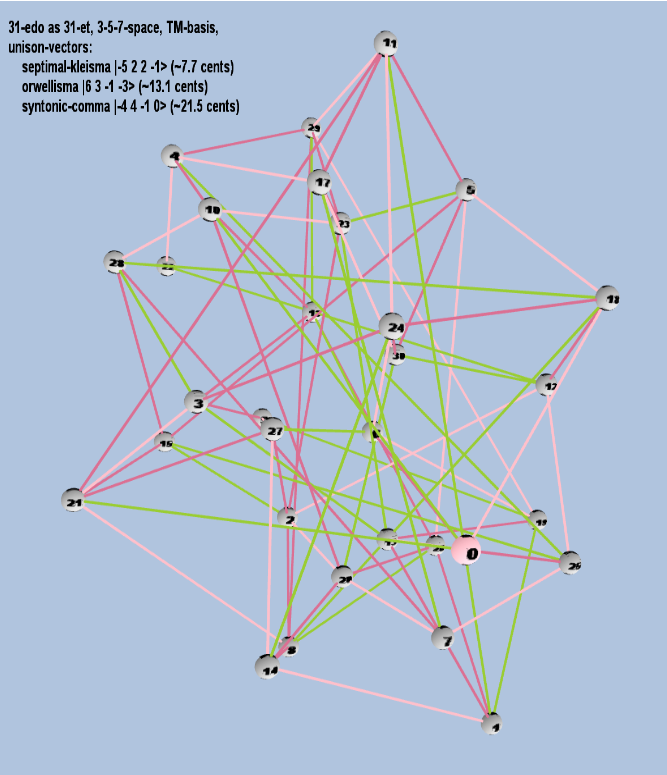
Example of a 3-dimensional TM-basis

31 ET/EDO in 3,5,7-space

name factors monzo ratio ~cents
septimal-kleisma 2-5 32 52 7-1 [ -5, 2, 2, -1> 225 / 224 7.711522991319706
orwellisma 26 33 5-1 7-3 [ 6, 3, -1, -3> 1,728 / 1,715 13.07356932395248
syntonic-comma 2-4 34 5-1 70 [-4, 4, -1, 0> 81 / 80 21.50628959671478

rectangular

Lattice: 3,5,7-space, TM-basis, 31-edo, rectangular geometry, letter notation Lattice: 3,5,7-space, TM-basis, 31-edo, rectangular geometry, logarithmic 31-edo degree notation

triangular

Lattice: 3,5,7-space, TM-basis, 31-edo, triangular geometry, letter notation Lattice: 3,5,7-space, TM-basis, 31-edo, triangular geometry, logarithmic 31-edo degree notation

In the same way that 1-dimensional (linear) lattices require a second dimension in which to warp the lattice, turning the line into a spiral or circle, 2-dimensional lattices require a third dimension in which to warp the lattice, to form a helix or (as in all examples above) a torus. Lattices which already have 3 or more dimensions in their basic geometry (rectangular or triangular) also require an additional dimension in which to warp, but these higher dimensions are not easily perceivable visually. The result is what Brian McLaren and Joe Monzo have termed "crumpled-napkin" geometry; two views of the same example are shown below.

crumpled-napkin

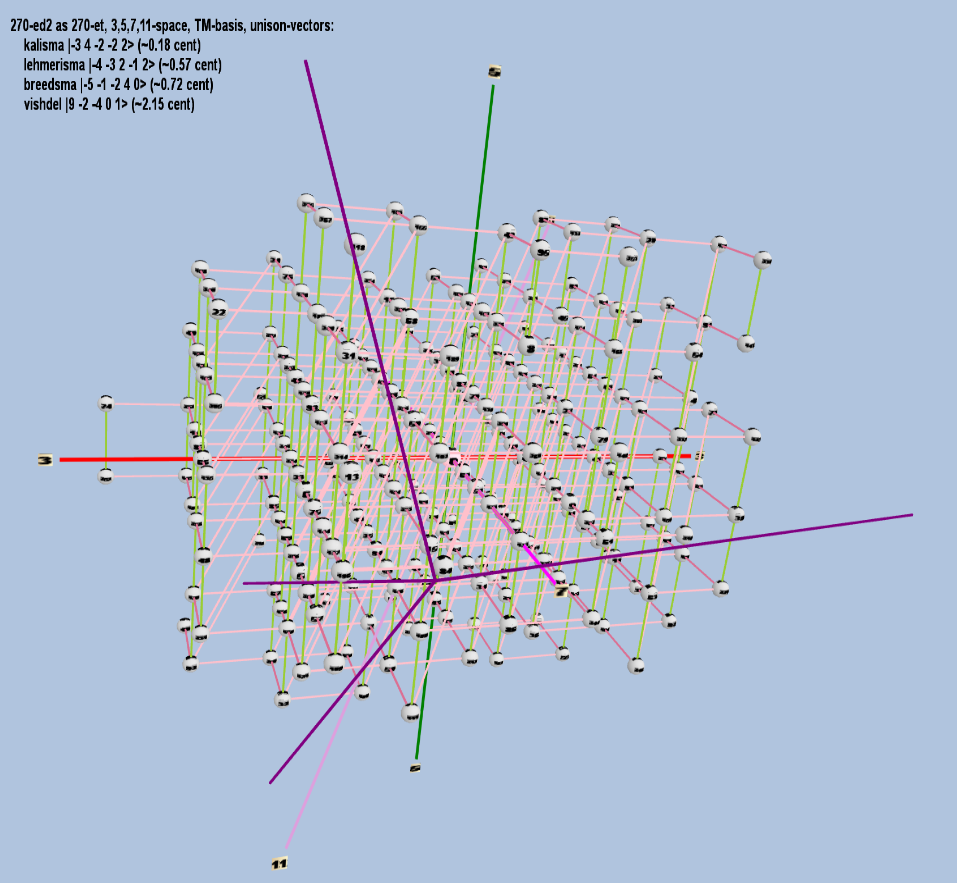
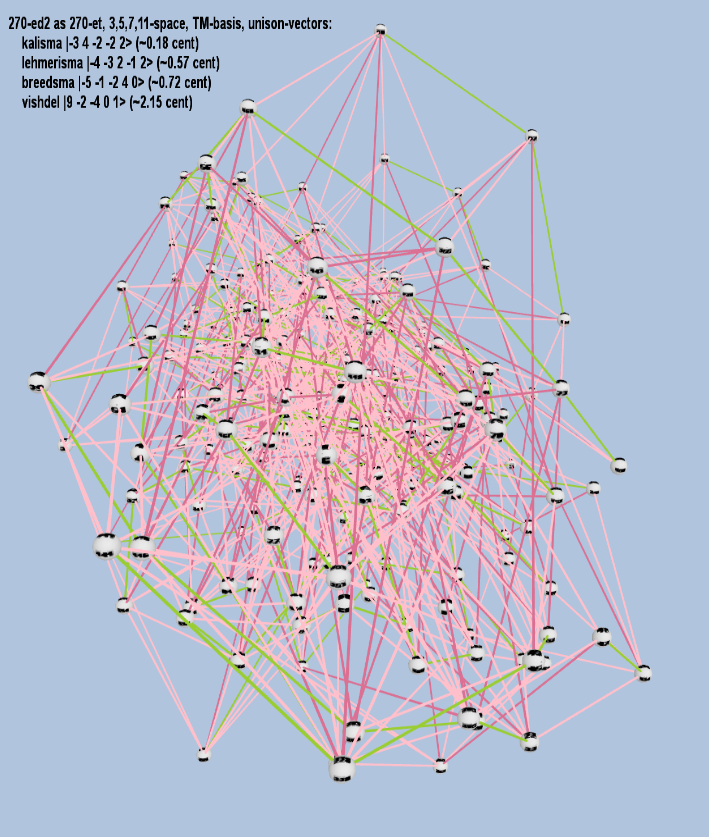
Lattice: 3,5,7-space, TM-basis, 31-edo, closed-curved crumpled-napkin geometry, letter notation Lattice: 3,5,7-space, TM-basis, 31-edo, closed-curved crumpled-napkin geometry, logarithmic 31-edo degree notation

Example of a 4-dimensional TM-basis

270-edo (tredeks) is used as an illustration here because of its excellence as a simpler integer replacement for cents in the 11-limit.

270 ET/EDO

name factors monzo ratio ~cents
kalisma 2-3 34 5-2 7-2 112 [-3 4 -2 -2 2> 9,801 / 9,800 0.1766475231436913
lehmerisma 2-4 3-3 52 7-1 112 [-4 -3 2 -1 2> 3,025 / 3,024 0.5724033938959937
breedsma 2-5 3-1 5-2 74 110 [ -5 -1 -2 4 0> 2,401 / 2,400 0.7211972814427758
vishdel 29 3-2 5-4 70 111 [9 -2 -4 0 1> 5,632 / 5,625 2.1530851746424933

rectangular

Lattice: 3,5,7,11-space, TM-basis, 31-edo, rectangular geometry, logarithmic 31-edo degree notation

Below are two views of the 5-dimensional crumpled-napkin geometry for this tonespace.

crumpled-napkin

Lattice: 3,5,7-space, TM-basis, 31-edo, closed-curved crumpled-napkin geometry, letter notation Lattice: 3,5,7-space, TM-basis, 31-edo, closed-curved crumpled-napkin geometry, logarithmic 31-edo degree notation
. . . . . . . . .

The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.

support level