19-tone equal-temperament and 1/3-comma meantone / 19-edo / 19-ed2
19edo on standard 5-line musical staff

Below is a list of pitches in 19-edo, with letter nominals using "C" as the reference (as in the music notation illustrated above), showing the enharmonic equivalences which occur in 19-edo:
letter 19-edo nominal degree ~cents exact cents C 19 1200 1200 B#/Cb 18 1136.842105 1136 + 16/19 B 17 1073.684211 1073 + 13/19 Ax/Bb 16 1010.526316 1010 + 10/19 A#/Bbb 15 947.3684211 947 + 7/19 A 14 884.2105263 884 + 4/19 Gx/Ab 13 821.0526316 821 + 1/19 G#/Abb 12 757.8947368 757 + 17/19 G 11 694.7368421 694 + 14/19 Fx/Gb 10 631.5789474 631 + 11/19 F#/Gbb 9 568.4210526 568 + 8/19 F 8 505.2631579 505 + 5/19 E#/Fb 7 442.1052632 442 + 2/19 E 6 378.9473684 378 + 18/19 Dx/Eb 5 315.7894737 315 + 15/19 D#/Ebb 4 252.6315789 252 + 12/19 D 3 189.4736842 189 + 9/19 Cx/Db 2 126.3157895 126 + 6/19 C#/Dbb 1 63.15789474 63 + 3/19 C 0 0 0
An early and very simple proposal for a meantone tuning was 1/3-comma meantone and its close relative 19-edo. The earliest reference to a tuning which may be 19-edo is in the 5th Treatise of the Berkeley Manuscript -- although it is not clear exactly how the tuning described here worked, it does state that the tone is divided into 3 parts, which are apparently equal. The earliest alleged use of this tuning is by Guillaume Costeley in 1558, in his chanson Seigneur Dieu ta pitié. The most well-known early reference, to both tunings, was by Salinas in 1577.
1/4-comma meantone is the only tuning of the meantone family which provides a "tone" which is the exact mean between the two sizes of 5-limit just-intonation "tones" -- the "tone" of 1/3-comma meantone and 19-edo is therefore smaller than the true meantone, and closer in size to the 10:9 ratio, the smaller of the two just-intonation tones.
Meantone family tunings are historically very important to the development of Western music, as the paradigms postulated by "common-practice" music-theory to a great extent depend on the elimination or tempering-out of the syntonic-comma, which is probably the most prominent feature of all meantones.
Note that while in the familiar 12-edo tuning (which also is a member of the meantone family) there is a complete set of enharmonic equivalents, such that all 7 notes which have "flats" can also be "spelled" as 7 different notes which have "sharps" along with a nominal one step lower, in all other meantones the "flats" are higher in pitch than supposedly enharmonically-equivalent "sharps". This is the opposite of the case in the much older pythagorean tuning, and also the opposite of the case in the "expressive intonation" which has been widely taught in Eurocentric schools of playing since Beethoven's time (around 1800).
Tunings of the meantone family were the closest thing to a "standard" tuning in most of Europe from approximately 1500 to 1700, and were still commonly found on keyboards (especially organs) until about 1850. It would be fair to say that most instrumental music of the Renaissance and Baroque periods was intended to be played in some form of meantone, and even after the growth in popularity of well-temperaments for keyboards after 1700, some form of meantone (generally more like 1/6-comma or 55-edo) was usually still intended for orchestral music.
During Mozart's lifetime (late 1700s) orchestral players began using an "expressive intonation" which veered back towards Pythagorean, and Beethoven's musical language certainly encouraged the spread of 12-edo, but to some extent meantone persisted in orchestral playing until approximately around the time of Wagner (mid-to-late 1800s). After the nearly universal adoption of 12-edo, the loss of meantone was lamented by Mahler in the early 1900s. (see Monzo, A Century of New Music in Vienna.)
The 1/3-comma meantone "5th" -- the generator -- is (3/2) / ((81/80)(1/3)). Using vector addition, that's:
2^ 3^ 5^
[ -1 1 0 ] = Pythagorean ("pure") "perfect 5th" of 3:2 ratio
- [ -4/3 4/3 -1/3 ] = (2-4345-1)(1/3) = (81/80)(1/3)
-----------------------
[ 1/3 -1/3 1/3 ] = 1/3-comma meantone "5th"
= ~694.7862377 cents.
This has the effect of tempering out the syntonic-comma so that it vanishes, thus making 4 "5ths" minus 2 "8ves" fairly close to the just "major 3rd":
2^ 3^ 5^
[ 4/3 -4/3 4/3 ] = 4 1/3-comma meantone "5ths"
- [ 2 0 0 ] = 2 "8ves"
-----------------------
[ -2/3 -4/3 4/3 ] = 1/3-comma meantone "major 3rd" = ~379.1449507 cents.
The difference between the just-intonation and the 1/3-comma meantone "major-3rds" is:
2^ 3^ 5^
[ -2/3 -4/3 4/3 ] = 1/3-comma meantone "major 3rd"
- [ -2 0 1 ] = just-intonation "major 3rd" of 5:4 ratio
-----------------------
[ 4/3 -4/3 1/3 ] = error of 19-edo from just-intonation "major-3rd" = - ~7.168763 cents.
This amount is exactly 1/3 of a syntonic-comma.
Assuming "octave"-equivalence (i.e., the exponents of 2 are irrelevant to the construction of the scale, so i've added 2-2 to the vector here to put the note into the reference "octave"), the next note in the cycle after the "5th", that of +2 generators, is the "whole-tone" 2(2/3) 3-(2/3) 5(2/3) = ~189.5724753 cents. If we compare this to the two just-intonation "whole-tones", subtracting the meantone from the larger pythagorean 9/8 and subtracting the smaller 5-limit 10/9 from the meantone, we find where the meantone lies between the two just-intonation "whole-tones":
2^ 3^ 5^
[ -3 2 0 ] = 9/8
- [ 2/3 -2/3 2/3 ] = 1/3-comma meantone
-----------------------
[ -2 2 -2/4 ] = ~14.3375264 cents = exactly 2/3-comma smaller than 9/8.
2^ 3^ 5^
[ 2/3 -2/3 2/3 ] = meantone
- [ 1 -2 1 ] = 10/9
-----------------------
[ -1/3 4/3 -1/3 ] = ~7.168763199 cents = exactly 1/3-comma larger than 10/9.
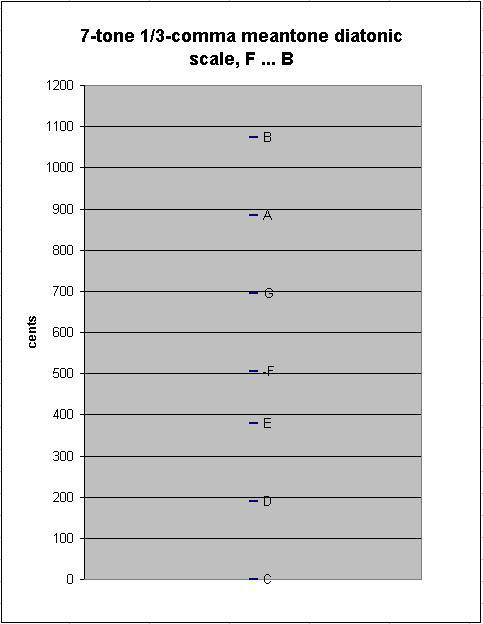
The 7-tone diatonic scale in 1/3-comma meantone contains only two "step" sizes: the ~189.5724753-cent "whole-tone" described above, between C:D, D:E, F:G, G:A, and A:B, and the ~126.0688117-cent "diatonic semitone" between E:F and B:C:
generator 8ves 2 3 5 ~cents
-1 1 * [-1/3 1/3 -1/3] 505.2137623 "F"
4 - -2 * [ 4/3 -4/3 4/3] 379.1449507 "E"
---------------------------
-5 3 * [-5/3 5/3 -5/3] 126.0688117 1/3-comma meantone diatonic semitone ("minor-2nd")
7-tone 1/3-comma meantone diatonic scale
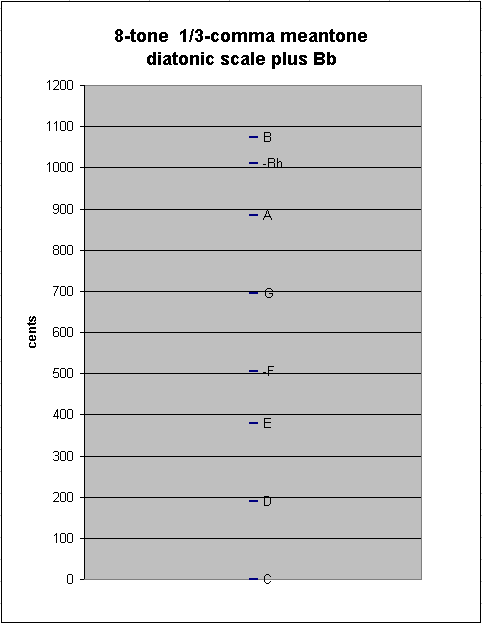
Introducing "Bb" into the scale causes a new between-degree interval to appear: the ~63.50366367-cent "chromatic semitone" between Bb:B :
generator 8ves 2 3 5 ~cents
5 -2 * [ 5/3 -5/3 5/3] 1073.931188 "B"
-2 - 2 * [-2/3 2/3 -2/3] 1010.427525 "Bb"
---------------------------
7 -4 * [ 7/3 -7/3 7/3] 63.50366367 1/3-comma meantone chromatic semitone ("augmented prime")
1/3-comma meantone diatonic scale with Bb
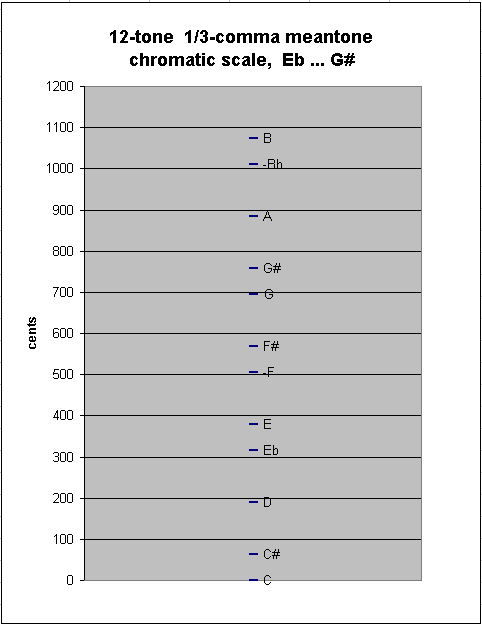
Continuing to add pitches at either end of the chain, we eventually come to the "typical" 12-tone chromatic scale used in Europe during the meantone era, from Eb to G#. This scale has as between-degree intervals only the two sizes of semitones, chromatic and diatonic:
Adding one more note to either end results in another new between-degree interval, of ~62.565148 cents, as between G#:Ab in my example here:
generator 8ves 2 3 5 ~cents
-4 3 * [ -4/3 4/3 -4/3] 820.8550493 "Ab"
8 - -4 * [ 8/3 -8/3 8/3] 758.2899013 "G#"
---------------------------
-12 7 * [-12/3 12/3 -12/3] 62.565148 1/3-comma meantone "great" (enharmonic) diesis ("diminished-2nd")
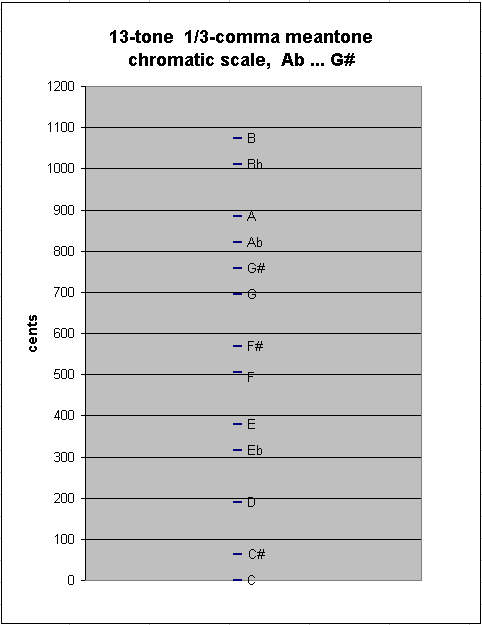
It can be seen both from the numbers and from the graph that this interval is almost the same size as the last one derived; thus, there is essentially no difference in 1/3-comma meantone between the chromatic semitone and the enharmonic diesis -- and in 19-edo, they are in fact exactly the same size:
generator 8ves 2 3 5 ~cents
7 -4 * [ 7/3 -7/3 7/3] 63.50366367 1/3-comma meantone chromatic semitone ("augmented prime")
-12 - 7 * [-12/3 12/3 -12/3] 62.565148 1/3-comma meantone "great" (enharmonic) diesis ("diminished-2nd")
---------------------------
19 -11 * [ 19/3 -19/3 19/3] 0.938515663 1/3-comma meantone "small diesis" ("magic-comma")
One may continue to add 6 more notes in this manner without encountering a step-size which is radically different, thus because of the similarity of the 1/3-comma meantone chromatic semitone and enharmonic diesis, the division of the "8ve" tends to become evened-out:
19-tone 1/3-comma meantone chromatic scale

It can be seen from the graph directly above that this divides the "8ve" into 19 nearly-identical steps, and so it can be easily inferred that other new notes will be quite similar to those already produced, and that the system is thus in effect closed at 19 notes.
If a 20th note is added, for example -7 (Cb), there occurs a new, tiny between-degree interval, which is in fact the same "small diesis" calculated above: ~0.938515663 (= ~15/16) cent, ocurring between Cb and B# :
generator 8ves 2 3 5 ~cents
12 -6 * [12/3 -12/3 12/3] 1137.434852 "B#"
-7 - 5 * [-7/3 7/3 -7/3] 1136.496336 "Cb"
---------------------------
19 -11 * [19/3 -19/3 19/3] 0.938515663 1/3-comma meantone small diesis ("magic-comma")
For all intents and purposes, this difference may be disregarded, so that 19-edo can be considered identical to a 19-tone chain of 1/3-comma meantone. ~0.938515663 / 19 = ~0.049395561 cent: this miniscule amount is the difference between the 1/3-comma meantone "5th" and the 19-edo "5th".
20-tone 1/3-comma meantone scale

Below is a graph showing the pitch-height of this 20-tone chain of 1/3-comma meantone. The red line connects the two pitches which are close together.
20-tone 1/3-comma meantone chain
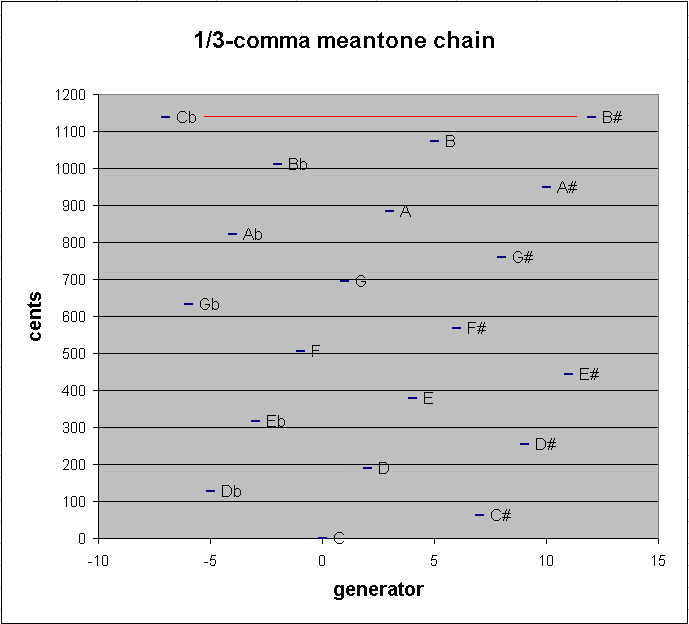
19-edo is audibly indistinguishable from 1/3-comma meantone. 2(11/19) = 696.7741935 cents. Using vector addition again to compare the 1/3-comma meantone "5th" with the 19-edo "5th", we get a difference between the two of:
2^ 3^ 5^
[ 1/3 -1/3 1/3 ] = ~694.7862377 cents = 1/3-comma meantone "5th"
- [ 11/19 0 0 ] = ~694.7368421 cents = 19-EDO "5th"
-----------------------
[ -14/57 -1/3 1/3 ] = 19-edo "5th" "-" 1/3-comma meantone "5th"
= ~0.049395561 cent = ~1/20 cent
Thus, 2(19/3) * 3-(19/3) * 5(19/3) acts as a unison-vector which is not tempered out in 1/3-comma meantone, and it acts as a unison-vector which is tempered out in 19-edo. Because this interval is so small, it really makes no difference whether or not it is "officially" tempered out: it will sound like a unison in either case.
Salinas in 1577 (De Musica, book 3, chapter 16) described 1/3-comma meantone with mathematical exactitude for the first time. First he constructed a 24-tone just-intonation system, which had duplicate pairs of some pitches a syntonic-comma apart, the higher of which was labeled "superius" and the lower "inferius". Then he explained the amount of tempering for each of the meantone pitches. By tempering out the full comma which exists between the 5 pairs of "superius/inferius" pitches, he reduced the number of pitches from 24 to 19.
Below is a lattice which places Salinas's 1/3-comma meantone in prime-space and shows its relationship to his just-intonation system, as he describes it; the slanted arrows represent the syntonic-comma:
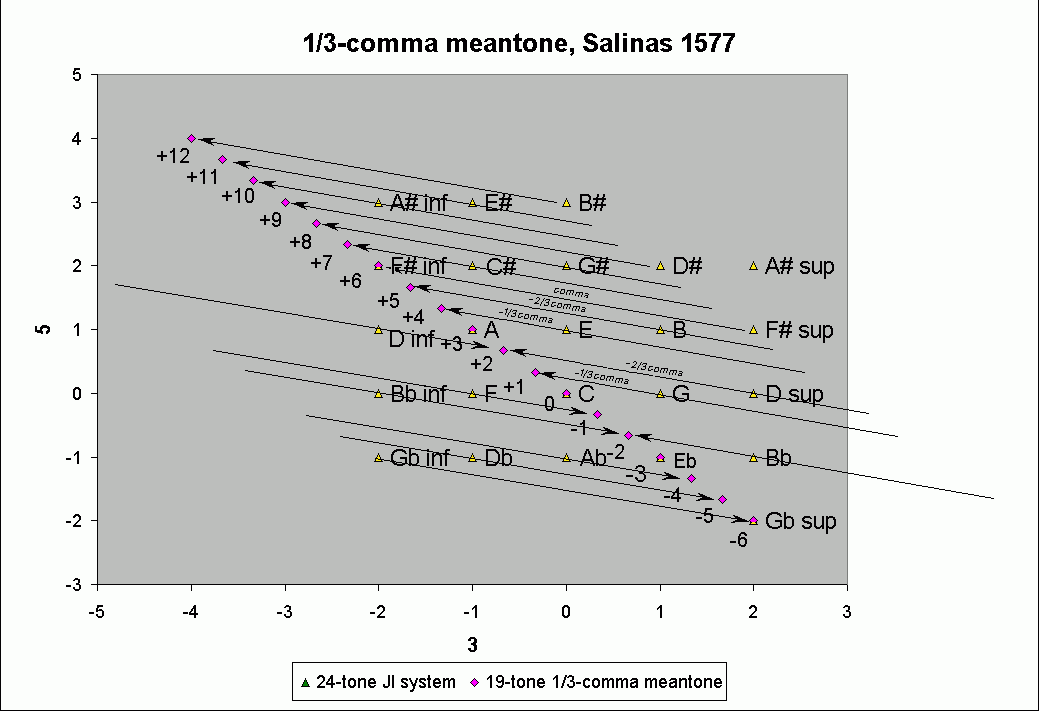
It can be seen that all pitches of the meantone are either exactly those of Salinas's just-intonation system, or are 1/3, 2/3, or a full comma higher or lower than those in his just-intonation system.
He goes on to explain how to temper the 24-note just-intonation system into 19 notes of 2/7-comma meantone, and then also into 19 notes of 1/4-comma meantone, the latter of which he finally declares to be the best of the three temperaments.
Salinas did not explicitly mention the equal nature of the 8ve-division in his 1/3-comma meantone, but he would have known about it himself and it can be inferred from the measurements he described. The 19-tone systems of the 2/7-comma and 1/4-comma meantone are less equally-spaced, being rather closer to subsets of 50-edo and 31-edo, respectively.
Below is a 5-limit triangular lattice-diagram of just-intonation ratios, showing an example 19-tone periodicity-block which is defined and bounded by 2 unison-vectors, the syntonic-comma and the magic-comma, which can form a basis to be tempered into 19-edo. Data given for each lattice-point are the note's ratio representation, 19-edo degree, and letter-name (with accidental where needed).
19-edo 5-limit meantone unison-vectors: monzo ratio name [ 4, -1> 81:80 syntonic-comma [-1, 5> 3125:3072 magic-comma C = 1:1 125:96 125:64 375:256 7 ----- 18 ---- 10 E# B# Fx / \ / \ / \ / \ / \ / \ 25:24 25:16 75:64 225:128 1 ----- 12 ----- 4 ---- 15 C# G# D# A# / \ / \ / \ / / \ / \ / \ / 5:3 5:4 15:8 45:32 14 ----- 6 ----- 17 ----- 9 A E B F# / \ / \ / \ / / \ / \ / \ / 4:3 1:1 3:2 9:8 8 ----- 0 ----- 11 ---- 3 F C G D / \ / \ / \ / / \ / \ / \ / 16:15 8:5 6:5 9:5 2 ---- 13 --- 5 ----- 16 Db Ab Eb Bb
In fact this structure perfectly describes Salinas's just-intonation structure as described above.
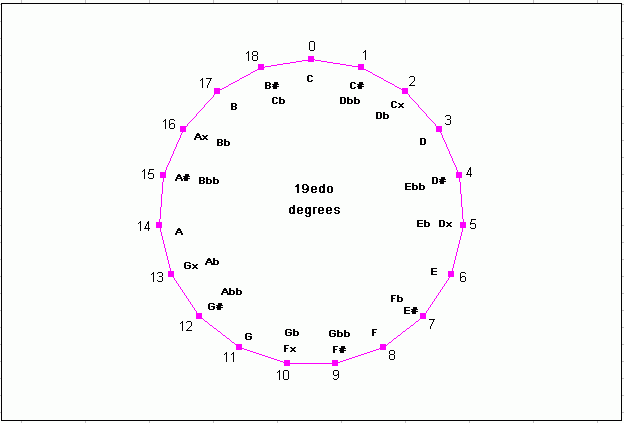
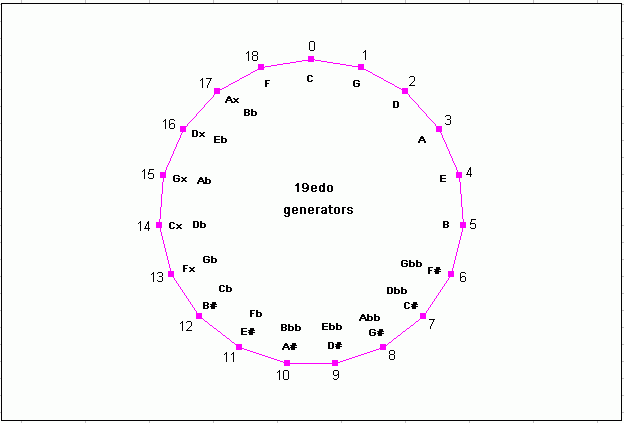
Below are two circular graphs of 19-edo in its typical meantone usage (be aware that 19-edo also belongs to other temperament families!). One graph arranges the pitches in scalar order by 1/3-tone scale degree generators around the circle, and the other arranges the pitches in order of diatonic-5th generators; both show the enharmonic equivalences which occur in 19-edo.
19-edo circle-of-degrees
19-edo circle-of-5ths
Mappings of some JI ratios in 19-edo
Below is a table showing how some of the most common just-intonation ratios are mapped to 19-edo, using the closest-fit mappings:
====================================
edomap.py (c)2008-12-23 by Joe Monzo
====================================
please enter edo: any displaced mappings? ... 0=no, 1=yes : 0
19 -edo floating-point mappings:
prime edo-steps step-error edo-map
2 = 19.000000 +0.00 --> 19
3 = 30.114288 -0.11 --> 30
5 = 44.116634 -0.12 --> 44
7 = 53.339744 -0.34 --> 53
11 = 65.729201 +0.27 --> 66
13 = 70.308355 -0.31 --> 70
17 = 77.661794 +0.34 --> 78
19 = 80.710623 +0.29 --> 81
23 = 85.947677 +0.05 --> 86
29 = 92.301639 -0.30 --> 92
31 = 94.129730 -0.13 --> 94
37 = 98.979614 +0.02 --> 99
41 = 101.793488 +0.21 --> 102
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 19 = 1200.000000 cents <-- 1200.000000 + 0.0 cents
map 3 --> 30 = 1894.736842 cents <-- 1901.955001 - 7.2 cents
map 5 --> 44 = 2778.947368 cents <-- 2786.313714 - 7.4 cents
map 7 --> 53 = 3347.368421 cents <-- 3368.825906 -21.5 cents
map 11 --> 66 = 4168.421053 cents <-- 4151.317942 +17.1 cents
map 13 --> 70 = 4421.052632 cents <-- 4440.527662 -19.5 cents
map 17 --> 78 = 4926.315789 cents <-- 4904.955410 +21.4 cents
map 19 --> 81 = 5115.789474 cents <-- 5097.513016 +18.3 cents
map 23 --> 86 = 5431.578947 cents <-- 5428.274347 + 3.3 cents
map 29 --> 92 = 5810.526316 cents <-- 5829.577194 -19.1 cents
map 31 --> 94 = 5936.842105 cents <-- 5945.035572 - 8.2 cents
map 37 --> 99 = 6252.631579 cents <-- 6251.344039 + 1.3 cents
map 41 --> 102 = 6442.105263 cents <-- 6429.062406 +13.0 cents
--------------
examples: (highest to lowest in pitch, according to mapping)
ratio --> 19 -edo mapping:
ratio cents error edo cents name
65536:32805 = 1198.0 +65.1 --> 20/19 = 1263.2 (minimal just dim-2)
1048576:531441 = 1176.5 +86.6 --> 20/19 = 1263.2 (pythagorean dim-2nd)
2:1 = 1200.0 +0.0 --> 19/19 = 1200.0 (octave)
2025:1024 = 1180.4 -43.6 --> 18/19 = 1136.8 (small just aug-7th)
125:64 = 1158.9 -22.1 --> 18/19 = 1136.8 (minimal just aug-7th)
31:16 = 1145.0 -8.2 --> 18/19 = 1136.8 (31st harmonic)
48:25 = 1129.3 +7.5 --> 18/19 = 1136.8 (small just dim-8ve)
256:135 = 1107.8 +29.0 --> 18/19 = 1136.8 (minimal just dim-8ve)
4096:2187 = 1086.3 +50.5 --> 18/19 = 1136.8 (pythagorean diminished-8ve)
21:11 = 1119.5 -45.8 --> 17/19 = 1073.7 (undecimal diminished-8ve)
243:128 = 1109.8 -36.1 --> 17/19 = 1073.7 (pythagorean major-7th)
15:8 = 1088.3 -14.6 --> 17/19 = 1073.7 (15th harmonic, large just major-7th, 5*3)
13:7 = 1071.7 +2.0 --> 17/19 = 1073.7 (tridecimal superminor-7th)
50:27 = 1066.8 +6.9 --> 17/19 = 1073.7 (small just maj-7th)
24:13 = 1061.4 +12.3 --> 17/19 = 1073.7 (tridecimal major-7th)
11:6 = 1049.4 +24.3 --> 17/19 = 1073.7 (undecimal submajor[neutral]-7th)
20:11 = 1035.0 -24.5 --> 16/19 = 1010.5 (undecimal superminor[neutral]-7th)
29:16 = 1029.6 -19.1 --> 16/19 = 1010.5 (29th harmonic)
9:5 = 1017.6 -7.1 --> 16/19 = 1010.5 (just minor-7th)
16:9 = 996.1 +14.4 --> 16/19 = 1010.5 (pythagorean minor-7th)
59049:32768 = 1019.6 -72.2 --> 15/19 = 947.4 (pythagorean aug-6th)
3645:2048 = 998.0 -50.7 --> 15/19 = 947.4 (large just aug-6th)
225:128 = 976.5 -29.2 --> 15/19 = 947.4 (small just augmented-6th)
7:4 = 968.8 -21.5 --> 15/19 = 947.4 (7th harmonic, septimal subminor-7th)
216:125 = 946.9 +0.4 --> 15/19 = 947.4 (large just dim-7)
19:11 = 946.2 +1.2 --> 15/19 = 947.4 (nondecimal supermajor-6th)
12:7 = 933.1 +14.2 --> 15/19 = 947.4 (septimal supermajor-6th)
128:75 = 925.4 +22.0 --> 15/19 = 947.4 (small just dim-7th)
22:13 = 910.8 +36.6 --> 15/19 = 947.4 (tridecimal augmented-6th)
2048:1215 = 903.9 +43.5 --> 15/19 = 947.4 (minimal just dim-7)
32768:19683 = 882.4 +65.0 --> 15/19 = 947.4 (pythagorean dim-7th)
27:16 = 905.9 -21.7 --> 14/19 = 884.2 (27th harmonic, pythagorean major-6th)
5:3 = 884.4 -0.1 --> 14/19 = 884.2 (just major-6th)
18:11 = 852.6 -31.5 --> 13/19 = 821.1 (undecimal superminor[neutral]-6th)
13:8 = 840.5 -19.5 --> 13/19 = 821.1 (13th harmonic)
21:13 = 830.3 -9.2 --> 13/19 = 821.1 (tridecimal ?)
8:5 = 813.7 +7.4 --> 13/19 = 821.1 (just minor-6th)
128:81 = 792.2 +28.9 --> 13/19 = 821.1 (pythagorean minor-6th)
11:7 = 782.5 +38.6 --> 13/19 = 821.1 (undecimal augmented-5th)
6561:4096 = 815.6 -57.7 --> 12/19 = 757.9 (pythagorean augmented-5th)
405:256 = 794.1 -36.2 --> 12/19 = 757.9 (large just aug-5th)
25:16 = 772.6 -14.7 --> 12/19 = 757.9 (25th harmonic, small just augmented-5th)
14:9 = 764.9 -7.0 --> 12/19 = 757.9 (septimal subminor-6th)
17:11 = 753.6 +4.3 --> 12/19 = 757.9 (septendecimal diminished-6th)
20:13 = 745.8 +12.1 --> 12/19 = 757.9 (tridecimal augmented-5th)
192:125 = 743.0 +14.9 --> 12/19 = 757.9 (large just dim-6)
1024:675 = 721.5 +36.4 --> 12/19 = 757.9 (small just dim-6th)
16384:10935 = 700.0 +57.9 --> 12/19 = 757.9 (minimal just dim-6)
262144:177147 = 678.5 +79.4 --> 12/19 = 757.9 (pythagorean dim-6th)
3:2 = 702.0 -7.2 --> 11/19 = 694.7 (pythagorean perfect-5th)
19:13 = 657.0 +37.8 --> 11/19 = 694.7 (nondecimal doubly-augmented-4th)
16:11 = 648.7 -17.1 --> 10/19 = 631.6 (11th subharmonic, undecimal diminished-4th)
13:9 = 636.6 -5.0 --> 10/19 = 631.6 (tridecimal diminished-5th)
23:16 = 628.3 +3.3 --> 10/19 = 631.6 (23rd harmonic)
10:7 = 617.5 +14.1 --> 10/19 = 631.6 (septimal large-tritone)
64:45 = 609.8 +21.8 --> 10/19 = 631.6 (just diminished-5th)
1024:729 = 588.3 +43.3 --> 10/19 = 631.6 (pythagorean diminished-5th)
729:512 = 611.7 -43.3 --> 9/19 = 568.4 (pythagorean augmented-4th)
45:32 = 590.2 -21.8 --> 9/19 = 568.4 (large just augmented-4th)
7:5 = 582.5 -14.1 --> 9/19 = 568.4 (septimal small-tritone)
25:18 = 568.7 -0.3 --> 9/19 = 568.4 (small just aug-4th)
18:13 = 563.4 +5.0 --> 9/19 = 568.4 (tridecimal augmented-4th)
11:8 = 551.3 +17.1 --> 9/19 = 568.4 (11th harmonic, undecimal sub-augmented-4th)
15:11 = 537.0 -31.7 --> 8/19 = 505.3 (undecimal large-4th)
4:3 = 498.0 +7.2 --> 8/19 = 505.3 (pythagorean perfect-4th)
17:13 = 464.4 +40.8 --> 8/19 = 505.3 (septendecimal 4th)
177147:131072 = 521.5 -79.4 --> 7/19 = 442.1 (pythagorean aug-3rd)
10935:8192 = 500.0 -57.9 --> 7/19 = 442.1 (large just aug-3rd)
675:512 = 478.5 -36.4 --> 7/19 = 442.1 (small just aug-3rd)
21:16 = 470.8 -28.7 --> 7/19 = 442.1 (21st harmonic, septimal-4th, 7*3)
125:96 = 457.0 -14.9 --> 7/19 = 442.1 (minimal just aug-3rd)
13:10 = 454.2 -12.1 --> 7/19 = 442.1 (tridecimal diminished-4th)
9:7 = 435.1 +7.0 --> 7/19 = 442.1 (septimal supermajor-3rd)
41:32 = 429.1 +13.0 --> 7/19 = 442.1 (41st harmonic)
32:25 = 427.4 +14.7 --> 7/19 = 442.1 (small just dim-4th)
512:405 = 405.9 +36.2 --> 7/19 = 442.1 (minimal just dim-4)
8192:6561 = 384.4 +57.7 --> 7/19 = 442.1 (pythagorean diminished-4th)
14:11 = 417.5 -38.6 --> 6/19 = 378.9 (undecimal diminished-4th)
81:64 = 407.8 -28.9 --> 6/19 = 378.9 (pythagorean major-3rd)
5:4 = 386.3 -7.4 --> 6/19 = 378.9 (5th harmonic, just major-3rd)
16:13 = 359.5 +19.5 --> 6/19 = 378.9 (tridecimal major[neutral]-3rd)
11:9 = 347.4 +31.5 --> 6/19 = 378.9 (undecimal neutral-3rd)
39:32 = 342.5 -26.7 --> 5/19 = 315.8 (39th harmonic, 13*3)
6:5 = 315.6 +0.1 --> 5/19 = 315.8 (just minor-3rd)
19:16 = 297.5 +18.3 --> 5/19 = 315.8 (19th harmonic)
32:27 = 294.1 +21.7 --> 5/19 = 315.8 (pythagorean minor-3rd)
19683:16384 = 317.6 -65.0 --> 4/19 = 252.6 (pythagorean augmented-2nd)
1215:1024 = 296.1 -43.5 --> 4/19 = 252.6 (large just aug-2nd)
13:11 = 289.2 -36.6 --> 4/19 = 252.6 (tridecimal diminished-3rd)
75:64 = 274.6 -22.0 --> 4/19 = 252.6 (small just augmented-2nd)
7:6 = 266.9 -14.2 --> 4/19 = 252.6 (septimal subminor-3rd)
37:32 = 251.3 +1.3 --> 4/19 = 252.6 (37th harmonic)
15:13 = 247.7 +4.9 --> 4/19 = 252.6 (tridecimal augmented[neutral]-2nd)
144:125 = 245.0 +7.7 --> 4/19 = 252.6 (large just dim-3)
8:7 = 231.2 +21.5 --> 4/19 = 252.6 (septimal tone, supermajor-2nd)
256:225 = 223.5 +29.2 --> 4/19 = 252.6 (small just dim-3rd)
4096:3645 = 202.0 +50.7 --> 4/19 = 252.6 (minimal just dim-3)
65536:59049 = 180.4 +72.2 --> 4/19 = 252.6 (pythagorean dim-3rd)
9:8 = 203.9 -14.4 --> 3/19 = 189.5 (pythagorean major-2nd/tone)
10:9 = 182.4 +7.1 --> 3/19 = 189.5 (just minor-tone)
11:10 = 165.0 +24.5 --> 3/19 = 189.5 (undecimal small-tone/submajor-2nd)
35:32 = 155.1 -28.8 --> 2/19 = 126.3 (35th harmonic, 7*5)
12:11 = 150.6 -24.3 --> 2/19 = 126.3 (undecimal large-semitone)
13:12 = 138.6 -12.3 --> 2/19 = 126.3 (tridecimal minor-2nd)
14:13 = 128.3 -2.0 --> 2/19 = 126.3 (tridecimal major-2nd)
15:14 = 119.4 +6.9 --> 2/19 = 126.3 (septimal chromatic-semitone)
16:15 = 111.7 +14.6 --> 2/19 = 126.3 (just diatonic-semitone)
17:16 = 105.0 +21.4 --> 2/19 = 126.3 (17th harmonic, septendecimal semitone)
256:243 = 90.2 +36.1 --> 2/19 = 126.3 (pythagorean minor-2nd/limma)
2187:2048 = 113.7 -50.5 --> 1/19 = 63.2 (pythagorean augmented-prime/apotome)
135:128 = 92.2 -29.0 --> 1/19 = 63.2 (large just aug-prime)
25:24 = 70.7 -7.5 --> 1/19 = 63.2 (small just aug-prime, chromatic-semitone)
33:32 = 53.3 +9.9 --> 1/19 = 63.2 (33rd harmonic, 11*3)
128:125 = 41.1 +22.1 --> 1/19 = 63.2 (large just dim-2, diesis)
2048:2025 = 19.6 +43.6 --> 1/19 = 63.2 (small just dim-2nd, diaschisma)
1:1 = 0.0 +0.0 --> 0/19 = 0.0 (prime, unison)
32805:32768 = 2.0 -65.1 --> -1/19 = -63.2 (large just aug-7th, skhisma)
some commas:
3-limit
ratio cents error edomap cents name temperament family
531441:524288 = 23.5 -86.6 --> -1/19 = -63.2 (pythagorean-comma) aristoxenean
5-limit
ratio cents error edo cents name
648:625 = 62.6 +0.6 --> 1/19 = 63.2 (major-diesis) diminished
16875:16384 = 51.1 -51.1 --> 0/19 = 0.0 (negri-comma)
250:243 = 49.2 +14.0 --> 1/19 = 63.2 (maximal-diesis) porcupine
128:125 = 41.1 +22.1 --> 1/19 = 63.2 (enharmonic-diesis) augmented
34171875:33554432 = 31.6 -94.7 --> -1/19 = -63.2 (ampersand-comma)
3125:3072 = 29.6 -29.6 --> 0/19 = 0.0 (magic-comma) magic
20000:19683 = 27.7 +35.5 --> 1/19 = 63.2 (tetracot-comma)
81:80 = 21.5 -21.5 --> 0/19 = 0.0 (syntonic-comma) meantone
2048:2025 = 19.6 +43.6 --> 1/19 = 63.2 (diaschisma) pajara
393216:390625 = 11.4 +51.7 --> 1/19 = 63.2 (wuerschmidt-comma)
2109375:2097152 = 10.1 -73.2 --> -1/19 = -63.2 (semicomma)
15625:15552 = 8.1 -8.1 --> 0/19 = 0.0 (kleisma) kleismic
32805:32768 = 2.0 -65.1 --> -1/19 = -63.2 (skhisma) schismic
76294:76256 = 0.9 +62.3 --> 1/19 = 63.2 (ennealimma (~ratio))
292300:292297 = 0.0 +694.7 --> 11/19 = 694.7 (atom (~ratio))
7-limit
ratio cents error edo cents name
36:35 = 48.8 +14.4 --> 1/19 = 63.2 (septimal-diesis)
49:48 = 35.7 -35.7 --> 0/19 = 0.0 (slendro diesis (7/6 : 8/7))
50:49 = 35.0 +28.2 --> 1/19 = 63.2 (tritonic diesis, jubilisma)
64:63 = 27.3 +35.9 --> 1/19 = 63.2 (septimal-comma)
225:224 = 7.7 -7.7 --> 0/19 = 0.0 (septimal-kleisma)
11-limit
ratio cents error edo cents name
22:21 = 80.5 +45.8 --> 2/19 = 126.3 ()
33:32 = 53.3 +9.9 --> 1/19 = 63.2 (undecimal-diesis)
45:44 = 38.9 -38.9 --> 0/19 = 0.0 ()
8192:8019 = 37.0 +26.2 --> 1/19 = 63.2 (pyth dim-5th: 11/8)
55:54 = 31.8 +31.4 --> 1/19 = 63.2 ()
56:55 = 31.2 -31.2 --> 0/19 = 0.0 ()
99:98 = 17.6 +45.6 --> 1/19 = 63.2 (mothwellsma)
100:99 = 17.4 -17.4 --> 0/19 = 0.0 (ptolemisma)
121:120 = 14.4 +48.8 --> 1/19 = 63.2 (biyatisma (11/10 : 12/11))
13-limit
ratio cents error edo cents name
40:39 = 43.8 +19.3 --> 1/19 = 63.2 ((5/3 : 13/8))
65:64 = 26.8 -26.8 --> 0/19 = 0.0 ((13/8 : 8/5))
6656:6561 = 24.9 +38.3 --> 1/19 = 63.2 (13/8 : pyth aug-5th)
91:90 = 19.1 -19.1 --> 0/19 = 0.0 (superleap)
144:143 = 12.1 -12.1 --> 0/19 = 0.0 ((18/11 : 13/8))
169:168 = 10.3 -10.3 --> 0/19 = 0.0 (dhanvantarisma)
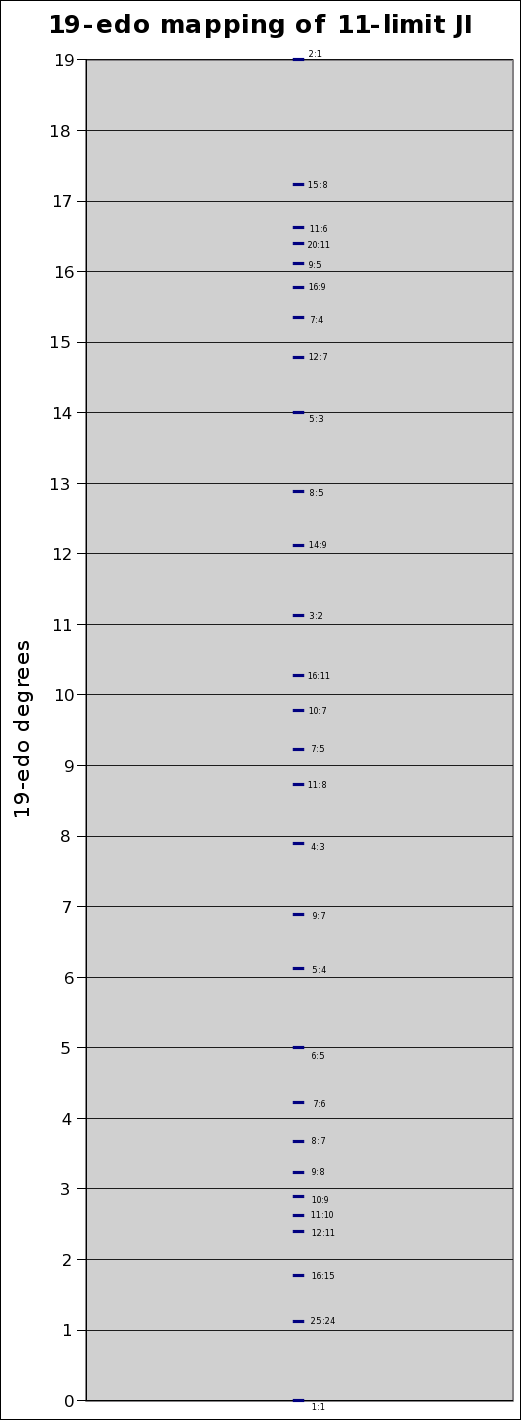
Below is a graph showing the degrees of 19-edo as the Y-axis grid, with the pitch of the JI ratios plotted against it:
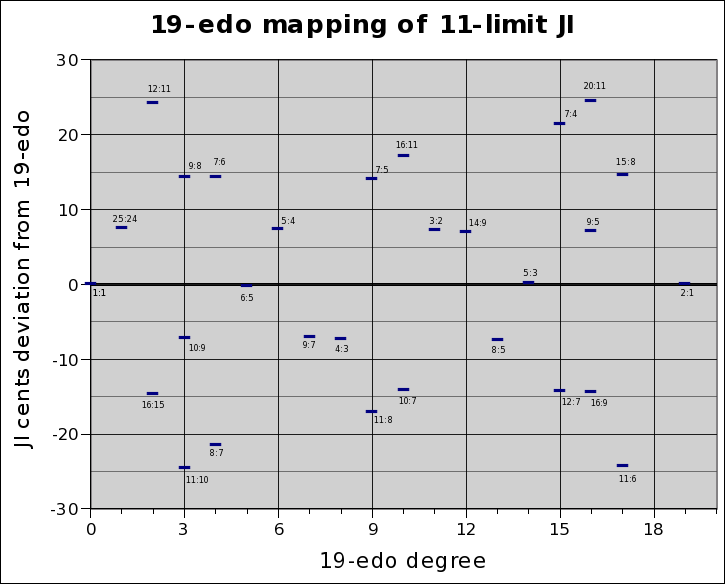
Below is a graph showing the degrees of 19-edo along the X-axis, with the Y-value of zero representing the pitch of the 19-edo degrees, and the deviation of the JI ratios from the 19-edo degrees plotted against that:
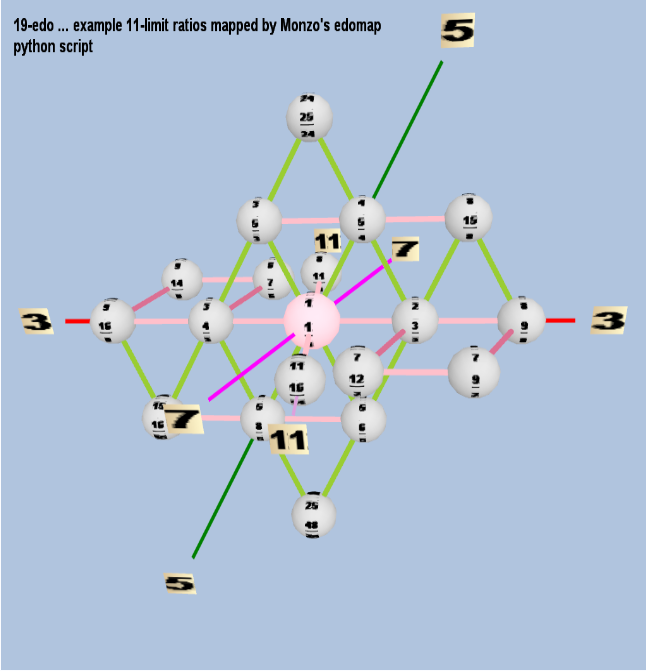
Below is a Tonescape® Lattice illustrating some of the ratios approximated by this mapping:
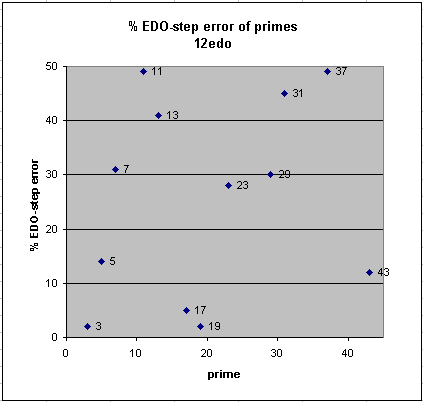
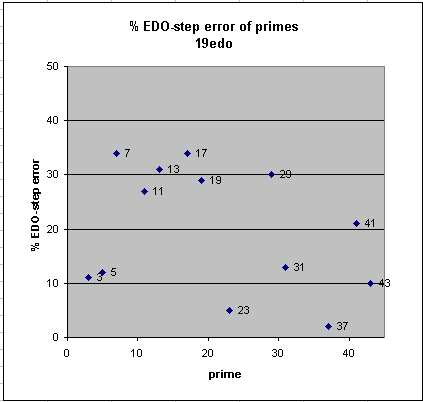
Below are graphs of the error of 12-edo and 19-edo for approximations to the prime-factors up to 43, given as a percentage of one degree of each tuning. It can easily be seen that the big improvements of 19-edo over 12-edo are the approximations to prime-factors 11, 13, 23, 31, and 37, and that 19-edo's approximations to 3, 17, and 19 are considerably worse than 12-edo's.
|
|
| 19=0 | 2:1 = 1:1 |
| 18 | 25:13 , 27:14 |
| 17 | 13:7 , 119:64 , 251:135 |
| 16 | 9:5 , 43:24 , 52:29, 95:53 , 147:82 |
| 15 | 19:11 , 121:70 , 140:81 , 401:232 |
| 14 | 5:3 |
| 13 | 8:5 , 45:28 , 143:89 , 188:117 |
| 12 | 14:9 , 17:11 , 31:20 , 79:51 , 110:71 |
| 11 | 3:2 , 118:79 , 121:81 , 239:160 |
| 10 | 13:9 , 36:25 , 229:159 |
| 9 | 7:5 , 18:13 , 25:18 , 318:229 |
| 8 | 4:3 , 79:59 , 241:180 , 320:239 |
| 7 | 9:7 , 31:24 , 71:55 |
| 6 | 5:4 , 56:45 , 61:49 , 117:94 |
| 5 | 6:5 |
| 4 | 7:6 , 15:13 , 22:19 , 59:51 , 81:70 |
| 3 | 9:8 , 10:9 , 19:17 , 29:26 , 135:121 , 299:268 , 328:294 |
| 2 | 13:12 , 14:13 , 55:53 , 71:66 , 199:18 5 , 270:251 |
| 1 | 26:25 , 27:26 , 28:27 , 307:296 |
| 0 | 1:1 |
| progressing to the right = greater accuracy of approximation and greater complexity | |
Below is a proposal for a new staff-notation based on 19-edo, where the naturals (nominals) are notated on thin lines and the sharps and flats on thick lines.

The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.
