Private lessons available in person in San Diego, or online using Discord: composition, music-theory, tuning-theory, piano, and all woodwinds (sax, clarinet, flute, bassoon, recorder). Current rates US$ 80 per hour (negotiable). Send an email to: monzojoe2 (AT) gmail. Also please consider making a donation to Tonalsoft using the PayPal button at the bottom of this page. Thank you.
HEWM notation
The acronym used by Joseph Monzo to stand for Helmholtz / Ellis / Wolf / Monzo notation (the long name was first used by Paul Erlich on the Tuning List).
Monzo's version of the HEWM notational system uses prime-factors and their exponents as accidentals placed before the note-heads, along with the following accidental symbols, whose intonational inflections are given in the table:
lower raise 2,3,5,7,11-monzo ratio ~cents b # [-11 7, 0 0 0> 2187:2048 113.6850061 v ^ [ -5 1, 0 0 1> 33:32 53.2729432 < > [ 6 -2, 0 -1 0> 64:63 27.2640918 - + [ -4 4, -1 0 0> 81:80 21.5062896
These symbols for the accidentals were chosen specifically with the view towards being able to communicate about rational tunings by email using the standard ASCII character set. The mathematical basis up to the 5-limit, and the process of prime-factorization, is described more fully in Monzo, JustMusic Prime-Factor Notation. This exposition will focus on the accidental symbols.
If indication of prime-factor 2 is required, it may simply be added to the list of exponents in the accidental. Normally octave-equivalence is assumed, so prime-factor 2 can simply be ignored, as it will be in the following discussion. In terms of the notation, this means that a letter-name, or any combination of a letter-name and accidentals, represents any "8ve" of that note. Thus, we are here dealing with pitch-classes as opposed to specific pitches.
(Monzo uses the monzo vector notation here in which each vector element is an exponent of a prime-factor, the prime series implied in order from left to right, beginning with 3. For example,
[ 1, > = 31 = 3 , [ 0, 1> = 51 = 5 , [ 1, 1> = 3151 = 15 , [-1, 1> = 3-151 = 5/3,
etc. Monzo uses "redundant coding" here to illustrate all four types of nomenclature: letter-names, prime-factor vectors, ratios, and cents. The math works out correctly for all four: add letters alphabetically, add elements of vectors, multiply ratios, and add cents. Ratios are thus the most difficult to comprehend of the group, and cents the least accurate.)
The Pythagorean basis - handling of prime-factor 3
Essentially, Monzo takes the historical pythagorean and diatonic origins of standard western musical notation as his starting point. The different powers (exponents) of prime-factor 3, create the nominals (notes with different letter-names) for the 7 notes of the diatonic scale:
letter F C G D A E B 3-monzo [-4,> [-3,> [-2,> [-1,> [0,> [1,> [2,> ratio 128/81 32/27 16/9 4/3 1/1 3/2 9/8 ~cents 792 294 996 498 0 702 204
Their ordering above, by exponent of prime-factor 3, creates a "chain of 5ths". Placed in order of pitch, these 7 notes compose the pythagorean diatonic scale, as illustrated below by the A-minor natural-minor scale which has historic precedence:
letter A B C D E F G 3-monzo [0,> [2,> [-3,> [-1,> [1,> [-4,> [-2,> ratio 1/1 9/8 32/27 4/3 3/2 128/81 16/9 ~cents 0 204 294 498 702 792 996
Incidentally, it can be seen that the Pythagorean diatonic semitone is thus 3-5 or [-5,> = 256:243 ratio = ~90 2/9 cents:
letter 3-monzo ratio ~cents
F [-4,> 128:81 792
- E - [ 1,> / 3:2 - 702
----- ------- -------- -----
= [-5,> 256:243 90
C [-3,> 32:27 294
- B - [ 2,> / 9:8 - 204
----- ------- ------ -----
= [-5,> 256:243 90
and that the Pythagorean "tone" is 32 = [2,> = 9:8 ratio = ~203 10/11 cents:
letter 3-monzo ratio ~cents
B [ 2,> 9:8 204
- A - [ 0,> / 1:1 - 0
----- ------- ------ -----
= [ 2,> 9:8 204
D [-1,> 4:3 498
- C - [-3,> / 32:27 294
----- ------- ------ -----
= [ 2,> 9:8 - 204 ... etc.
These two intervals are the step sizes of the Pythagorean scale. This scale was assumed as the theoretical standard in European music for about 1000 years, from c. 500 to c. 1500 AD. The standard reference is Boethius, de institutione musica (books 1, 2, 3, 4, 5).
Going back to the "chain of 5ths" presentation, adding a note to either end:
letter Bb F C G D A E B F# 3-monzo [-5,> [-4,> [-3,> [-2,> [-1,> [0,> [1,> [2,> [3,> ratio 256/243 128/81 32/27 16/9 4/3 1/1 3/2 9/8 27/16 ~cents 90 792 294 996 498 0 702 204 906
requires the use of an accidental: b on the flat (negative) side and # on the sharp (positive) side. Ignoring prime-factor 2 since we assume octave-equivalence, we may describe this as a change of "plus" or "minus" (which when using ratios means dividing or multiplying) 37 = [7,> = 2187:2048 = ~113 2/3 cents:
letter 3-monzo ratio ~cents F# [ 3,> 27:16 906 - F - [-4,> / 128:81 - 792 ----- ------- -------- ----- # = [ 7,> 2187:2048 114 Bb [-5,> 256:243 90 - B - [ 2,> / 9:8 - 204 ----- ------- --------- ----- b = [-7,> 2048:2187 -114
Essentially, # and b indicate chromatic alteration of diatonic scale tones within a Pythagorean (that is, 3-limit) context. They thus designate the Pythagorean chromatic semitone of ~113 2/3 cents.
(Note that the nomenclature of German cultural areas is different, in that it includes the 8th letter, H. See Monzo, The note "H" in German musical nomenclature for a detailed examination.)
Symbols for prime-factor 5
Examining the introduction of accidentals by increase in the prime series, the next set we find are + and -, which indicate the presence of prime-factor 5, and represent an intonational inflection of "plus" or "minus" 81:80 = [4, -1>, the syntonic comma of ~21 1/2 cents.
| E- [-3, 1> B- [-2, 1> F#- [-1, 1> C#- [0, 1> G#- [1, 1>
exponent 1 + 40:27 10:9 5:3 5:4 15:8
| 680 182 884 386 1088
|
| C [-3, 0> G [-2, 0> D [-1, 0> A [0, 0> E [1, 0>
of 0 + 32:27 16:9 4:3 1:1 3:2
| 294 996 498 0 702
|
| Ab+ [-3, -1> Eb+ [-2, -1> Bb+ [-1, -1> F+ [0, -1> C+ [1, -1>
5 -1 + 256:135 64:45 16:15 8:5 6:5
| 1108 610 112 814 316
|
-----|-------+--------------+-------------+-------------+-----------+------
| -3 -2 -1 0 1
e x p o n e n t o f 3
So it can be seen, for example, that the just major 3rd (with ratio 5:4) above C [-3, 0> , is E- [-3, 1> , so therefore:
letter 3,5-monzo ratio ~cents E- [-3, 1> 40:27 680 - E - [ 1, 0> / 3:2 - 702 ---- ---------- ------- ----- - = [-4, 1> 80:81 -22
And this C [-3, 0> itself has a counterpart a comma higher at C+ [1, -1> :
letter 3,5-monzo ratio ~cents C+ [ 1, -1> 6:5 316 - C - [-3, 0> / 32:27 - 294 ---- ---------- ------- ----- + = [ 4, -1> 81:80 22
As a parenthetical digression here, it is worth pointing out that the vast majority of music in the standard Euro-centric repertoire never distinguishes this interval, so that an A is always simply an A, a B is always simply a B, etc. This indicates that these composers always intended to temper out the syntonic comma (i.e., make it vanish).
The tuning systems implied by this all belong to the meantone family -- some typical EDOs are 12, 19, 24, 26, 31, 43, 45, 50, 55, 69, 74, 81, and 88-edo.
The tempering-out of this interval also has the effect of broadening the meaning of # and b in these tunings, as follows:
ratio ~cents
[ 7, 0> + [4, -1> = [11, -1> 177147 : 163840 135.1912957
[ 7, 0> 2187 : 2048 113.6850061
[ 7, 0> - [4, -1> = [ 3, 1> 135 : 128 92.17871646
[ 3, 1> - [4, -1> = [-1, 2> 25 : 24 70.67242686
[-1, 2> - [4, -1> = [-5, 3> 250 : 243 49.16613727
[-5, 3> - [4, -1> = [-9, 4> 20000 : 19683 27.65984767 etc.
So these intervals are all functionally identical in these types of tunings, and so, depending on the harmonic context, # and b can "mean" an intonational inflection by any of these 5-limit intervals. So any of these intervals (and by extension on either side, possibly some others as well) may be implied as the "chromatic semitone" in music of this repertoire.
With this broadening of meaning for "chromatic semitone", there is a corresponding broadening of meaning for "diatonic semitone" as well (See Monzo, Tempering out the syntonic comma for a detailed examination of this):
ratio ~cents
[ 3, -2> + [4, -1> = [ 7, -3> 2187 : 2000 154.7438645
[-1, -1> + [4, -1> = [ 3, -2> 27 : 25 133.2375749
[-5, 0> + [4, -1> = [-1, -1> 16 : 15 111.7312853
[-5, 0> 256 : 243 90.22499567
[-5, 0> - [4, -1> = [-9, 1> 20480 : 19683 68.71870608 etc.
So only a close analysis of the harmonic context of a given passage of music can disclose which of these are intended to be implied. Often, composers write chord progressions in which several of these ratios may be implied simultaneously, which blurs distinctions between them. Tuning theorists generally refer to this as "punning".
Using HEWM notation, a composer would not be able to create puns based on the syntonic comma, because the comma is indicated explicitly in the notation. The composer would have to find other intervals which are not designated in this notation, to choose for punning.
Now, back to the main narrative ...
Symbols for prime-factor 7
The next prime in the series is 7, and so the next set of accidentals we find are > and <, which represent the presence of prime-factor 7, by indicating an intonational inflection of widening or narrowing by 64:63, as follows:
Referring to the scale above, the 7th harmonic (or partial) of our reference pitch A [0, 0 0> would be notated as G< [0, 0 1>, to indicate that it is ~27 1/4 cents lower (flatter) than the G [-2, 0 0> we have already obtained in our basic scale, thus:
letter 3,5,7-monzo ratio ~cents G< [ 0, 0 1> 7:4 969 - G - [-2, 0 0> / 16:9 - 996 ---- ------------- ------ ----- < = [ 2, 0 1> 63:64 -27
And A [0, 0 0> itself would thus be the 7th harmonic of B> , as follows:
letter 3,5,7-monzo ratio ~cents B> [ 0, 0 -1> 8:7 231 - B - [ 2, 0 0> / 9:8 - 204 ---- ------------- ------ ----- > = [-2, 0 -1> 64:63 27
Note that meantone tunings provide an interval which is close to the 7th harmonic, namely the "augmented 6th" of +10 generators in the meantone "cycle of 5ths". Thus, for example, a meantone A# == HEWM Bb<. The use of "augmented 6th chords" by European "common-practice" composers thus seems to indicate a liking for the 4:5:6:7 sonority, as the proportion of the "augmented 6th chord" in meantone tuning very nearly approaches 4:5:6:7.
Symbols for prime-factor 11
The last set of new accidentals in my HEWM notation indicate the presence of prime-factor 11, by indicating an intonational inflection of "plus" or "minus" 33:32, as follows:
Referring again to the basic Pythagorean scale, the 11th harmonic (or partial) of our reference pitch A [0, 0 0 0> would be notated as D^ [0, 0 0 1>, to indicate that it is ~531/4 cents higher (sharper) than the D [-1, 0 0 0> we have already obtained in our basic scale, thus:
letter 3,5,7,11-monzo ratio ~cents D^ [ 0, 0 0 1> 11:8 551 - D - [-1, 0 0 0> / 4:3 - 498 ---- ---------------- ------- ----- ^ = [ 1, 0 0 1> 33:32 53
And A [0, 0 0 0> itself would thus be the 11th harmonic of Ev , as follows:
letter 3,5,7,11-monzo ratio ~cents Ev [ 0, 0 0 -1> 16:11 649 - E - [ 1, 0 0 0> / 3:2 - 702 ---- ---------------- ------- ----- v = [-1, 0 0 -1> 32:33 -53
The tempered version: "simplified HEWM" based on 72edo
The rational basis of Monzo's HEWM notation translates very well into his 72edo notation:
lower raise inflection cents b # semitone 100 v ^ 1/4-tone 50 < > 1/6-tone 331/3 - + 1/12-tone 162/3
The 72edo version of HEWM simplifies things a great deal, because of the fact that multiples of certain symbols may equal other symbols, and thus sets of symbols which equal opposites cancel each other out and may be omitted from the notation.
Here's a great example of how the JI version of HEWM differs from the 72edo version:
Example:
Let's say we want to find the notation for the ratio 42:25, assuming that C = 1/1.
The first thing to do on the spreadsheet is to make sure that there's a zero next to "C" in the column of cyan cells near the top. This defines "C" as 1/1.
Then put in the target ratio. Whether using the method of inputting "comma" exponents or inputting the notation directly, the result will be the same:
2 3 5 7 11
target ratio: [ 1 1, -2 1 0> 42/25 898.2
HEWM: B bb - [ 15 -9, 0 0 0> 32768/19683 882.4
--------------------
[-14 10, -2 1 0> 413343/409600 15.7
< - [ -6 2, 0 1 0> 63/64 -27.3
--------------------
[ -8 8, -2 0 0> 6561/6400 43.0
+ - [ -4 4, -1 0 0> 81/80 21.5
--------------------
[ -4 4, -1 0 0> 81/80 21.5
+ - [ -4 4, -1 0 0> 81/80 21.5
--------------------
[ 0 0, 0 0 0> 1/1 0.0
So the JI HEWM notation for 42:25 is Bbb<++.
This is simplified in 72edo HEWM, because in 72edo, < = -- and > = ++, so we have Bbb<>, and the <> cancel each other out, leaving us with just Bbb.
In the JI version of HEWM, > and ++ are not the same, and so therefore all the symbols must be employed for precision.
Daniel Wolf's version of HEWM
The references at the end of Monzo, JustMusic prime-factor notation also mentions Daniel Wolf's version of HEWM, which inspired my version and in concept is identical to mine, with additional symbols for the prime-factors up to 23. He was kind enough to send me a detailed commentary on this, which appears below the graphic.
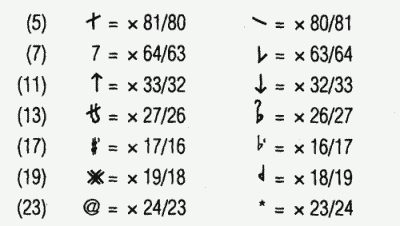
monzo
2 3 5 7 11 13 17 19 23 ratio ~cents
[-11 7, 0 0 0, 0 0 0, 0> 2187:2048 113.6850061 (symbol: the pythagorean # and b)
[ -4 4, -1 0 0, 0 0 0, 0> 81:80 21.5062896
[ 6 -2, 0 -1 0, 0 0 0, 0> 64:63 27.2640918
[ -5 1, 0 0 1, 0 0 0, 0> 33:32 53.2729432
[ -1 3, 0 0 0, -1 0 0, 0> 27:26 65.33734083
[ -4 0, 0 0 0, 0 1 0, 0> 17:16 104.9554095
[ -1 -2, 0 0 0, 0 0 1, 0> 19:18 93.6030144
[ 3 1, 0 0 0, 0 0 0, -1> 24:23 73.6806536
(Dr. Wolf has since retracted his advocacy for most of these symbols ... see his detailed comment below.)
Note that Wolf's symbols for prime-factor 5, 7, and 11 are very similar to mine. Also, note that he cleverly alludes to # and b for both prime-factors 17 and 19, whose inflections are both larger than the others and in the vicinity of a semitone.
In private communication, Dr. Wolf sent me the following update on his notational ideas:
I believe that we are in substantial agreement about notation. I like the historical approach, assuming octave equivalence, retaining the staff and using the series of fifths with seven nominals and two accidentals to represent a pythagorean sequence. Further, because I am a vocally oriented composer (and most of the instruments I play -- early winds, javanese rebab -- are voice-like in their pitch orientation), hearing from interval to interval, and tending to compose in a locally tonal but globally less-tonal way, I need to have invariant interval sizes: when I see a perfect fifth on the staff, without any modifications, I want to imagine a perfect fifth and not have to go through extraordinary mental gymnastics in order to figure out that it should actually be a comma-shy or comma-too-big.
This is not to ignore the fact that such pythagorean sequences can be mapped to an indefinite number of linear temperaments. In doing so, it may be useful to establish conventions of equivalence such as that found in meantone, where four ascending fifths are octave-equivalent to a just third (or in a skhismatic temperament where eight descending fifths do the same job).
When we wish to use tunings using intervals other than those found in a pythagorean tuning (or tempered equivalent thereof), then I advocate the use of additional accidental, indicating "comma" shifts from the pythagorean values. "Comma" is taken here broadly to indicate simply small intervals, with my preference to intervals with powers of two or three on one side of the ratio. The accidentals should come in clear pairs, either logical pairs (plus/minus) or graphic inversions.
In 1/1 I proposed a series of such accidentals. I stand by the symbols printed there through the 11-limit and have used them successfully with performers for over twenty years. The rest were thought up in haste in the days of daisy wheel printers and the limitations of a fixed set of characters; consequently, I do not stand by the particular graphics but the principles respresented by the signs remain valid. I will here propose some improvements to the graphics, but with the caveat that I have not yet found it neccessary to use such a notation, as my own music in JI has either been restricted to an 11-limit, or has gone so far beyond such a limit as to require a notation with some combination of ratios, exact frequency, and/or cent deviations from 12tet..
For shifts of 81/80 and 80/81, the syntonic comma, I use plus and minus signs respectively. This follows Erv Wilson, from whom I have also taken the practice of slanting significantly broadened horizontal strokes to ca. 45 degrees for increased readability and distinction from the staff lines. The horizontal stroke on the plus sign slants upward, that on the minus sign downward, the direction of the slant intended to increase the sense of direction conveyed by the interval. (I find that building a bit of redundancy into a notation is not a significant violation of my need for elegance in a notation).
For shifts of 63/64 and 64/63, the septimal comma, indicating ratios involving a factor 7, I use a numeral seven and its inversion. In ASCII, one can either use a "7" and a capital letter "L", but the greater-than and less-than signs (>,<) are pretty good substitutes. This seems to be an uncontroversial accidental, although those who prefer to notate the septimal minor seventh as an augmented sixth might well have a different opinion. (In 31tet, you can have it both ways: an augmented sixth has the same size as a minor seventh diminished by the interval equivalent in that temperament to the septimal comma, in this case one step of 31tet).
With the introduction of ratios involving a factor 11, I had, initially, to decide upon an orientation. The tone found 11/8 above a given tonic is almost exactly a quartertone between the perfect fourth and the augmented fourth above a given tone. Consequently, I could notate the 11/8 as either a fourth with an accidental raising by the interval 33/32 or as an augmented fourth diminished by the interval 729/704. I went with the simpler ratio and the added bonus that I would probably encounter fewer compound accidentals (i.e. . I notate this accidental with up and down arrows, following a common convention for notating quartertones.
At this point, I should note that the graphics selected for the the syntonic and unadecimal commas may be confused with those used in one of the current 72tet notations (there are several competing systems out there, none of which can be considered standard; I suppose that the recent advocacy of 72 by conductor and composer Hans Zender might push things in his direction, but I'll do a wait and see on this!) . In some of these systems, arrows are used for 12th tone deviations, which are very close in size to a syntonic comma, and a modified square root sign is used for the quartertone accidental. In contrast, both the Ben Johnston system for JI and the one described here use pluses and minuses for the syntonic comma -- we just disagree about the content of the set of pitches _without_ accidentals. I could cop out and simply say that my interest is in notating extended Just Intonations and the 72tet-ers can do their own thing, but the affinity of 72 for creating a near-just environment is not to be undervalued, and the notation described here functions identically to the Sims system when used in 72tet. It is equally efficient and just differs in the choice of graphics.
However, I'm willing to offer support for my choice of graphics, and one piece of explicit criticism for the Sims set. When I wrote my item for 1/1, I was writing my dissertation and supporting myself by teaching Junior-year Algebra in a Catholic Girl's Priory School in Southern California. At the time, I was convinced about the septimal accidentals, but wasn't sure whether pluses/minus were to be assigned to syntonic commas and up/down arrows to the 11-limit commas or vice versa. Erv Wilson had prepared me to like pluses and minuses at the smaller comma, pluses and minus were used in some of the important 19th century theory to indicate syntonic commas, and I had seem some quartertone scores with arrows, but that was hardly conclusive. So I made a totally unscientific poll on the subject and asked 124 Catholic Girl's Priory School 11th graders their opinion on the question:
"In your opinion, which of the following signs better indicates a larger quantity: (a) an arrow pointed upward (by means of a graphic of same drawn in white chalk on a green board) or (b) a plus sign (with this graphic drawn by similar means)?
The answer to this wholly unscientific poll of was clear: 102 chose (a), the upward-pointing arrow, 20 chose (b), the plus sign, and the remaining two were apparently agnostic.
So I went with the scheme described above.
And oh yes, my explicit criticism of the Sims: the modified square root signs are too large, and I find them, personally, to be ugly.
As mentioned before, the signs in the 1/1 article (by the way, although the editors of the journal call it "one-one" when pronouncing the name of their journal, following the pronunciation favored by Partch and Harrison for musical ratios, there are minority schools of practice where the name is pronounced as either "one to one" (which is somewhat sporting), "one over one" (which is too focused on power for my taste) or "one on one"; but then, maybe the name is not in English in the first place: the German eins zu eins shares the sporting connotation, while eins durch eins or eins über eins both have an historical-political aftertaste; the Hungarian egy egy, on the other hand, sounds enough like fingernails scraping against a clean, dry chalkboard to convince me that Magyar was not a pronounciation choice foreseen by said editors, but I digress: enough of that!) were made hastily, under primitive technological circumstances and are herefore, hereby und hiermit retracted immediately and irrovocably.
For ratios involving the factor 13, I propose to notate the intervals 26/27 and 27/26 with a question mark and an inverted question mark. The association of things tredecimal with strangness is not unknown (just ask anyone of us who happen to have been born on the 13th of September) and a question mark suggests this quality well. In the 1/1 item, I tried, unhappily, to combine question marks with sharps and flats; I now find the question marks to be adequate on their own. Fortunately, Spanish punctuation requires the inverted question mark
Ratios involving factors of 17 and 19 represent very small deviations from the accidentals found in the original pythagorean set. Again, as in the unadecimal accidental, one has an orientation issue with which to deal, but in this case there is no advantage vis a vis compounding accidentals, but I can go with the simplest ratios. In 1/1, I proposed adding a comma or apostrophe attached to a sharp, flat or natural for 17/16 and 16/17. This was, in itself, not objectionable for the sharp-sighted, but the signs for ratios of 19 (513/512 and 512/513) were just plain silly. I propose instead to keep sharp, flats, and naturals and simply add 17 or 19 above or below the accidental to indicate modifications by the relevant ratio in the direction of the numeral relative to the pythagorean accidental. For example, a C proceeded by a sharp with a seventeen above it would represented the frequency of C multiplied by 17/16. (You could also think of it as C# (2187/2048) multiplied by 2176/2187, but the simpler ratios seem more useful to me). This notation can be extended arbitrarily upward to ratios based on higher prime numbers.
There is more to be discussed -- for example, the problems of notating pitches related by several factors. At a certain point, the signage does get unwieldy (that point was rapidly reached in trying to notate a hebdomekontany!) and one might as well go with some combination of explicit ratios, frequencies, and cent-deviations from 12tet. Also, I have to admit that I have also developed a number of notational shorthands that I constantly use while composing but have hesistated to spring on performers. The shorthand I use use most frequently is a composite flat and septimal lowering, where the top, horizontal, line of the numeral seven extends from the vertical shaft of the flat. I further admit to being fond of the look of my shorthand, but this falls squarely into the box of personal eccentricities, is part of my sketching hand, not my clean copy, and is not intended or suggested for wider use.
Dr. Daniel James Wolf
Composer, Budapest/Morro Bay
http://home.snafu.de/djwolf/
Manuel Op de Coul's version of HEWM
(used in his popular tuning programScala)
lower raise 2,3,5,7,11-monzo ratio ~cents b # [-11 7 0 0 0] 2187:2048 113.6850061 v ^ [ -5 1 0 0 1] 33:32 53.2729432 L 7 [ 6 -2 0 -1 0] 64:63 27.2640918 \ / [ -4 4 -1 0 0] 81:80 21.5062896
The Hauptmann / Helmholtz / Ellis / Eitz versions of HEWM
The version of HEWM described by Hermann Helmholtz and Alexander Ellis is in Ellis's 1875 English translation of Helmholtz, On The Sensations of Tone.
As Paul Erlich noted, "apparently the HEWM notation system traces it roots to Eitz in 1891 and still further back to Hauptmann". Dave Benson, course notes for Mathematics and Music (zip file), Chapter 5, p 116 and 117, gives an explanation of Eitz's notation:
Eitz devised a system of notation, used in Barbour, which is convenient for describing scales based around the octave. His method is to start with the Pythagorean definitions of the notes and then put a superscript describing how many commas to adjust by. Each comma multiplies the frequency by a factor of 81/80.
As an example, the Pythagorean E, notated E0 in this system, is 81:64 of C, while E-1 is decreased by a factor of 81/80 from this value, to give the just ration of 80:64 or 5:4.
In this notation, the basic scale for just intonation is given by C0 - D0 - E-1 - F0 - G0 - A-1 - B-1 - C0 .
A common variant of this notation is to use subscripts rather than superscripts, so that the just major third in the key of C is E-1 instead of E-1.
Benson's footnote about Eitz:
Carl A. Eitz, Das mathematisch-reine Tonsystem, Leipzig, 1891. A similar notation was used earlier by Hauptmann and modified by Helmholtz.
Daniel Wolf also suggested that I point out that prolific German theorist Martin Vogel also uses + and - for the syntonic comma.
Gene Ward Smith on HEWM notation
Yahoo tuning group Message 47921 From: "Gene Ward Smith" Date: Mon Oct 13, 2003 12:47 pm Subject: HEWM
HEWM is Pythagorean plus 81/80, 64/63 and 33/32. To convert an 11-limit interval to it we can first convert to the [2,3/2,81/80,64/63,33/32] system and then rewrite the [2,3/2] part in terms of nominals and sharp/flats based on 2187/2048. The first conversion can be done as matrix math, or equivalently in terms of vals.
If we convert 2,3/2,81/80,64/63 and 33/32 to monzos and use these as rows of a matrix, we get
[ 1 0, 0 0 0> [-1 1, 0 0 0> [-4 4, -1 0 0> [ 6 -2, 0 -1 0> [-5 1, 0 0 1>
This is a unimodular matrix (it has integer entries and a determinant of one), and if we invert it we obtain a matrix whose columns are the vals w2, w3, w5, w7, w11 where
w2 = <1 1 0 4 4] w3 = <0 1 4 -2 -1] w5 = <0 0 -1 0 0] w7 = <0 0 0 -1 0] w11 = <0 0 0 0 -1]
Then for an 11-limit interval q, we have
q = 2^w2(q) (3/2)^w3(q) (81/80)^w5(q) (64/63)^w7(q) (33/32)^w11(q)
From this representation, conversion to HEWM is straightforward. The vals w2, w3, etc. can be thought of as dot products with the monzo for q.
Example:
For instance, if q = 77/75, it has monzo qm = [0 -1, -2 1 1>, then (w2, qm) = w2 . qm = 7 and (w3, qm) = -12. The others, up sign, are simply the corresponding 5, 7, and 11 monzo coordinates, or "valuations" in math-speak. We end up with
77/75 = 2^7 (3/2)^(-12) (81/80)^2 (64/63)^(-1) 33/32
If C is 1, then 2^7 (3/2)^(-12) is a Pythagorean comma down from 1, and a Pythagorean comma down is D (= 9/8) double flat. Hence 77/75 is D double flat, up two 81/80, down a 64/63 and up a 33/32 again.
Ideas to expand HEWM to 53-limit
(UPDATE: Please see the bottom section of this page for an appendix covering various different ways of thinking about this.) Here is an extension to get HEWM all the way to 53-limit. After some thought (see the speculations in the appendix below), I have decided to go along with Daniel Wolf's idea of using the smallest ratio for the deviation of the accidental symbol from the basic pythagorean nominals. Below I give a list of the odd harmonics up to the 53-limit, showing this "simplest ratio" usage of the accidentals. I still encourage others to experiment with the other commas listed in the appendix, but will offer this as my definitive specification for 53-limit JI HEWM notation.
monzo
lower raise prime 2 3, 5 7 11, 13 17 19, 23 29 31, 37 41 43, 47 53 ratio ~cents pyth base alteration
b # 3 [-11 7, 0 0 0, 0 0 0, 0 0 0, 0 0 0, 0 0 > 2187:2048 113.6850061 p1 up
- + 5 [ -4 4, -1 0 0, 0 0 0, 0 0 0, 0 0 0, 0 0 > 81:80 21.5062896 maj3 down
< > 7 [ 6 -2, 0 -1 0, 0 0 0, 0 0 0, 0 0 0, 0 0 > 64:63 27.2640918 min7 down
v ^ 11 [ -5 1, 0 0 1, 0 0 0, 0 0 0, 0 0 0, 0 0 > 33:32 53.2729432 p4 up
{ } 13 [ -1 3, 0 0 0, -1 0 0, 0 0 0, 0 0 0, 0 0 > 27:26 65.3373408 maj6 down
\ / 17 [ 1 2, 0 0 0, 0 -1 0, 0 0 0, 0 0 0, 0 0 > 18:17 98.9545922 maj2 down
( ) 19 [ -1 -2, 0 0 0, 0 0 1, 0 0 0, 0 0 0, 0 0 > 19:18 93.6030144 maj2 up
[ ] 23 [ 3 1, 0 0 0, 0 0 0, -1 0 0, 0 0 0, 0 0 > 24:23 73.6806536 p5 down
; ! 29 [ -8 2, 0 0 0, 0 0 0, 0 1 0, 0 0 0, 0 0 > 261:256 33.4871959 min7 up
? " 31 [ 5 0, 0 0 0, 0 0 0, 0 0 -1, 0 0 0, 0 0 > 32:31 54.9644275 p8 down
& % 37 [ -2 -2, 0 0 0, 0 0 0, 0 0 0, 1 0 0, 0 0 > 37:36 47.4340370 maj2 up
@ $ 41 [ 1 -4, 0 0 0, 0 0 0, 0 0 0, 0 1 0, 0 0 > 82:81 21.2424021 maj3 up
, ' 43 [ -7 1, 0 0 0, 0 0 0, 0 0 0, 0 0 1, 0 0 > 129:128 13.4727065 p4 up
: * 47 [ 4 1, 0 0 0, 0 0 0, 0 0 0, 0 0 0, -1 0 > 48:47 36.4483789 p5 down
. | 53 [ 1 3, 0 0 0, 0 0 0, 0 0 0, 0 0 0, 0 -1 > 54:53 32.3604571 maj6 down
example, showing odd harmonics above A
harmonic hewm-53
1 A
3 E
5 C#-
7 G<
9 B
11 D^
13 F#{
15 G#-
17 B\
19 B)
21 D<
23 E[
25 E#--
27 F#
29 G!
31 A?
33 A^
35 B<-
37 B%
39 C#{
41 C#$
43 D'
45 D#-
47 E:
49 F<<
51 F#\
53 F#.
For the music notation example below (created in MuseScore), I needed to add primes 59 and 61, so had to use two of the letters suggested as accidental symbols in the Appendix, so I will here provide an addition to the table above.
lower raise prime 2 3, 5 7 11, 13 17 19, 23 29 31, 37 41 43, 47 53 59, 61 67 71 ratio ~cents pyth base alteration s z 59 [ -2 5, 0 0 0, 0 0 0, 0 0 0, 0 0 0, 0 0 -1, 0 0 0 > 243:236 50.603345 maj7 down y k 61 [ -2 -5, 0 0 0, 0 0 0, 0 0 0, 0 0 0, 0 0 0, 1 0 0 > 244:243 7.109801 maj7 up
Below is an example of 61-limit JI HEWM, notated in MuseScore, showing the harmonics 32 to 63.

Other tempered versions of HEWM
Besides 72edo, other EDOs which give good approximations of various primes may also be used for HEWM. The "pythagorean" chain-of-5ths given for the nominals of each EDO below uses the patent-val (i.e., best / closest) mapping of prime-factor 3. Column 1 shows the generator number, column 2 shows the pythagorean-based notation, and column 3 shows in "x\EDO" form how many degrees of the EDO map to that note. The "HEWM accidentals" section shows the number of degrees of that EDO as "x\EDO" deviation from the "pythagorean" chain to reach that higher prime. All of those illustrated below are available with Matthew Tan's xen-tuner plugin for MuseScore 3.6 notation software.
37edo HEWM
37edo "pythagorean" chain-of-5ths nominals
gen note x\37 cents | compare pythagorean ~cents
|
5 B 36 1167.567_ | 1109.775004326937
4 E 14 454.054_ | 407.8200034615502
3 A 29 940.540_ | 905.8650025961633
2 D 7 227.027_ | 203.9100017307751
1 G 22 713.513_ | 701.9550008653875
0 C 0 0.0 | 0.0
-1 F 15 486.486_ | 498.04499913461245
HEWM accidentals:
| comparison with JI HEWM:
lower raise prime x\37 cents | ratio ~cents pyth base alteration
|
b # 3 6 194.594_ | 2187:2048 113.6850061 p1 up
- + 5 2 64.864_ | 81:80 21.5062896 maj3 down
< > 7 0 0.0 | 64:63 27.2640918 min7 down
v ^ 11 2 64.864_ | 33:32 53.2729432 p4 up
{ } 13 3 97.297_ | 27:26 65.3373408 maj6 down
\ / 17 4 129.729_ | 18:17 98.9545922 maj2 down
( ) 19 2 64.864_ | 19:18 93.6030144 maj2 up
[ ] 23 3 97.297_ | 24:23 73.6806536 p5 down
; ! 29 2 64.864_ | 261:256 33.4871959 min7 up
? " 31 2 64.864_ | 32:31 54.9644275 p8 down
& % 37 1 32.432_ | 37:36 47.4340370 maj2 up
@ $ 41 1 32.432_ | 82:81 21.2424021 maj3 up
, ' 43 1 32.432_ | 129:128 13.4727065 p4 up
: * 47 1 32.432_ | 48:47 36.4483789 p5 down
. | 53 2 64.864_ | 54:53 32.3604571 maj6 down
NOTE: Comparing the size of adjustment for the accidentals in 37edo-HEWM with those of JI-HEWM,
it appears that 37edo does not represent HEWM well. However, the reason for this is because
the size of the "5th" in 37edo is so much larger than pythagorean that the nominals themselves
are all much larger (much smaller for "F"). In actuality, 37edo approximates 5, 7, 11, and 13
so well that chords using these primes sound excellent in 37edo, and the HEWM notation adjusts
the tuning properly according to the table above.
download my 37edo xen-tuner/tuning file for MuseScore 3.6
41edo HEWM
41edo "pythagorean" chain-of-5ths nominals gen note x\41 ~cents | compare pythagorean ~cents +5 B 38 1112.195122 | 1109.775004326937 +4 E 14 409.756098 | 407.8200034615502 +3 A 31 907.317073 | 905.8650025961633 +2 D 7 204.878049 | 203.9100017307751 +1 G 24 702.439024 | 701.9550008653875 0 C 0 0.000000 | 0.0 -1 F 17 497.560976 | 498.04499913461245 HEWM accidentals: lower raise prime x\41edo cents b # 3 4 117.073 - + 5 1 29.268 < > 7 1 29.268 v ^ 11 2 58.537 { } 13 2 58.537 \ / 17 3 87.805 ( ) 19 3 87.805 [ ] 23 3 87.805 ; ! 29 1 29.268 ? " 31 2 58.537 & % 37 2 58.537 @ $ 41 1 29.268 , ' 43 0 0.0 : * 47 1 29.268 . | 53 1 29.268 s z 59 2 58.537 y k 61 0 0.0 download my 41edo xen-tuner/tuning file for MuseScore 3.6-->
87edo HEWM
41-limit JI may be expressed in 87edo HEWM as follows, noting that 17, 19, 23, and 29 are not represented well in 87edo.
87edo "pythagorean" chain-of-5ths nominals gen note x\87 ~cents | compare pythagorean ~cents 5 B 81 1117.241379 | 1109.775004326937 4 E 30 413.793103 | 407.8200034615502 3 A 66 910.344828 | 905.8650025961633 2 D 15 206.896552 | 203.9100017307751 1 G 51 703.448276 | 701.9550008653875 0 C 0 0.000000 | 0.0 -1 F 36 496.551724 | 498.04499913461245 HEWM accidentals: lower raise prime x\87edo cents b # 3 9 124.1 - + 5 2 27.6 < > 7 2 27.6 v ^ 11 4 55.2 { } 13 5 69.0 \ / 17 (7) 96.6 ( ) 19 (7) 96.6 [ ] 23 (5) 69.0 ; ! 29 (3) 41.4 ? " 31 4 55.2 & % 37 3 41.2 @ $ 41 1 13.8 download my 87edo xen-tuner/tuning file for MuseScore 3.6
311edo HEWM
41-limit JI may be expressed excellently in 311edo HEWM, as follows.
311edo "pythagorean" chain-of-5ths nominals
gen note x\311 ~cents | compare pythagorean ~cents
|
+5 B 288 1111.254019 | 1109.775004326937
+4 E 106 409.003215 | 407.8200034615502
+3 A 235 906.752412 | 905.8650025961633
+2 D 53 204.501608 | 203.9100017307751
+1 G 182 702.250804 | 701.9550008653875
+0 C 0 0.0 | 0.0
-1 F 129 497.749196 | 498.04499913461245
HEWM accidentals:
lower raise prime x\311edo ~cents
b # 3 30 115.8
- + 5 6 23.2
< > 7 7 27.0
v ^ 11 14 54.0
{ } 13 17 65.6
\ / 17 26 100.3
( ) 19 24 92.6
[ ] 23 19 73.3
; ! 29 6 23.2
? " 31 14 54.0
& % 37 12 46.3
@ $ 41 5 19.3
540edo HEWM
The full 53-limit JI spec of HEWM can be expressed in 540edo thus:
540edo "pythagorean" chain-of-5ths nominals
gen note x\540 ~cents | compare pythagorean ~cents
|
+5 B 500 1111.111111 | 1109.775004326937
+4 E 184 408.888889 | 407.8200034615502
+3 A 408 906.666667 | 905.8650025961633
+2 D 92 204.444444 | 203.9100017307751
+1 G 316 702.222222 | 701.9550008653875
0 C 0 0.0 | 0.0
-1 F 224 497.777778 | 498.04499913461245
HEWM accidentals:
lower raise prime x\540edo cents
b # 3 52 115.5_ (115 & 5/9)
- + 5 10 22.2_ ( 22 & 2/9)
< > 7 12 26.6_ ( 26 & 2/3)
v ^ 11 24 53.3_ ( 53 & 1/3)
{ } 13 30 66.6_ ( 66 & 2/3)
\ / 17 45 100.0
( ) 19 42 93.3_ ( 93 & 1/3)
[ ] 23 33 73.3_ ( 73 & 1/3)
; ! 29 15 33.3_ ( 33 & 1/3)
? " 31 25 55.5_ ( 55 & 5/9)
& % 37 21 46.6_ ( 46 & 2/3)
@ $ 41 9 20.0
, ' 43 6 13.3_ ( 13 & 1/3)
: * 47 17 37.7_ ( 37 & 7/9)
. | 53 15 33.3_ ( 33 & 1/3)
APPENDIX: Various earlier thoughts which led to the final 53-limit JI specification tabulated above
In order to avoid confusion here, as of 2022-0618, the Appendix has been separated into its own page, which see. There the reader will find various alternative ways of using the HEWM accidentals to specify tuning adjustments from pythagorean.
Please make a donation to help keep Tonalsoft online. A recurring monthly contribution would be apprecitated.
Thank you!
