The amalgamation of the Greater Perfect System and the Lesser Perfect System into one "complete" system. See Systema.
Shown below is a very general schematic illustrating the Greek names for the PIS in the diatonic genus, in descending order, along with approximate letter-names to help the Western reader to comprehend.
-
| A nete hyperbolaion
tetrachord |
hyperbolaion | G paranete hyperbolaion
|
| F trite hyperbolaion
- E nete diezeugmenon
| -
tetrachord | D paranete diezeugmenon D nete synemmenon |
diezeugmenon | | tetrachord
| C trite diezeugmenon C paranete synemmenon | synemmenon
| B paramese |
- - Bb trite synemmenon |
| A mese -
tetrachord |
meson | G lichanos meson
|
| F parhypate meson
- E hypate meson
|
tetrachord | D lichanos hypaton
hypaton |
| C parhypate hypaton
| B hypate hypaton
-
A Proslambanomenos
Below is a rendering of the PIS into modern staff-notation, using 4-note groups of eighth-notes to represent each tetrachord, with tetrachord names shown. The Greater Perfect System is shown with upward stems, and Lesser Perfect System with downward stems. Ties from the last note of one tetrachord to the first note of another indicate conjunct tetrachords.
Note that the intervallic structure of all tetrachords is identical, and that the complete system includes both of the notes which we would call "B" and "Bb". (See "mutation" for more on this.)
The tuning of the diatonic genus was almost always given by theorists as pythagorean, i.e., 3-limit, as shown in the following lattice-diagram:
Bb -- F --- C --- G --- D --- A --- E --- B
-5 -4 -3 -2 -1 0 1 2
exponent of 3
Below are two Tonescape® lattices of the PIS, one showing the ratios and one showing the letter nominals. Both lattices include prime-factor 2, since the PIS was always described in terms of absolute ratios and not with octave-equivalence assumed. The orientation of the axes has 2 on the horizontal and 3 on the vertical.
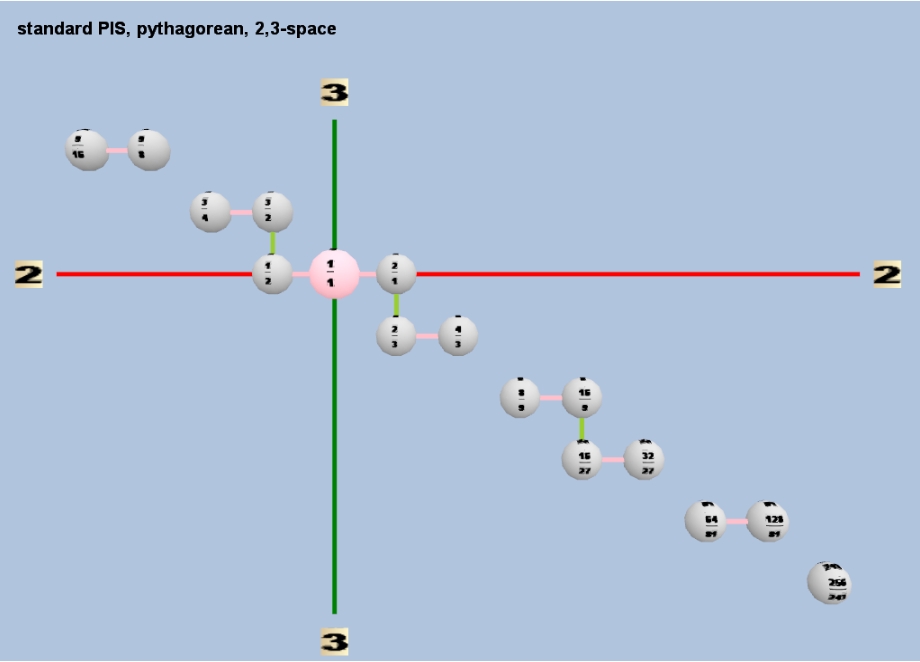
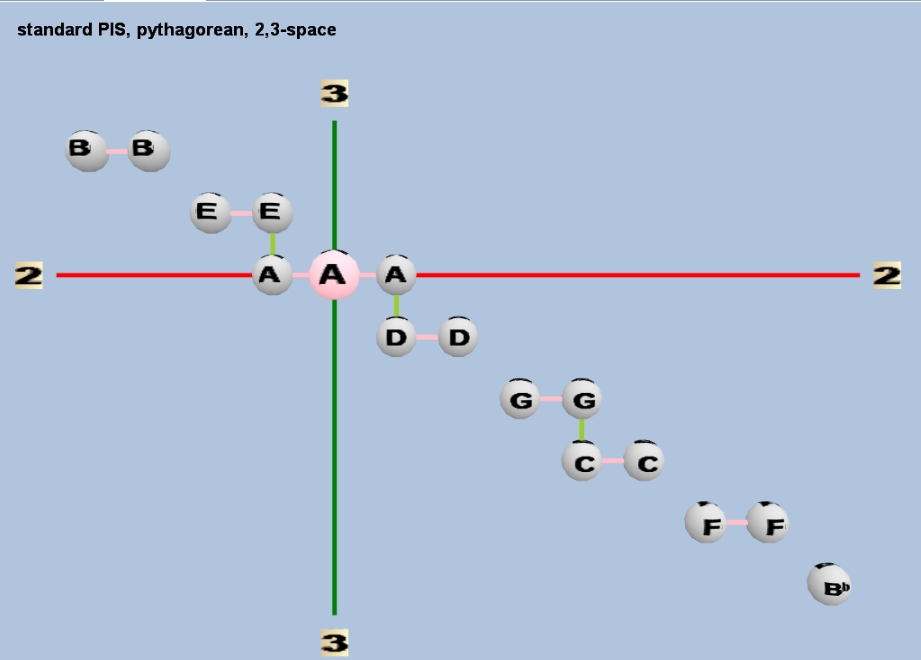
Below is an ASCII-text version of the same diagram, showing 2,3-monzo, ratio, letter nominal, and absolute cents value from 1/1 for each note:
lattice diagram:
PIS (Perfect Immutable System) - diatonic genus
pythagorean tuning
[8 -5> --
256:243 |
Bb |
+0090 |
| |
-- [7 -4>
128:81
F
+0792
|
[6 -4> --
64:81 |
F |
-0408 |
| |
-- [5 -3> -----
32:27 |
C |
+0294 |
| |
[4 -3> -- [4 -2>
16:27 16:9
C G
-0906 +0996
|
[3 -2> ---
8:9 |
G |
-0204 |
| |
-- [2 -1> ----
4:3 |
D |
+0498 |
| |
[1 -1> -- [1 0>
2:3 2:1
D A
-0702 +1200
|
[0 0> ------
1:1 |
A |
0000 |
| |
[-1 0> -- [-1 1>
1:2 3:2
A E
-1200 +0702
|
[-2 1> ---
3:4 |
E |
-0498 |
| |
-- [-3 2>
9:8
B
+0204
|
[-4 2>
9:16
B
-0996
This conception of the gamut of musical pitch resources lasted until the late 1400s in Europe, when Ramos and other theorists began writing about scales in which some of the pitches were retuned to 5-limit ratios.
Note that the two inner notes in each tetrachord could be retuned to other pitches in the chromatic and enharmonic genera, and even in different shades of the diatonic genus.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.