Private lessons with Joseph Monzo are available online via Discord / WhatsApp / Skype: composition, music-theory, tuning-theory, piano, and all woodwinds (sax, clarinet, flute, bassoon, recorder). Current rates US$ 80 per hour (negotiable). Send an email to: monzojoe (AT) gmail.
periodicity block
A periodicity-block is a geometrical model of a closed musical tuning system defined by unison-vectors. The term was used by Fokker in his lattice theory to describe one multi-dimensional region of the lattice which could substitute for another, by means of unison vectors. It is the unit-cell of a periodic tiling of the lattice.
This concept is allied with that of finity, which Monzo developed independently of Fokker. The periodicity blocks quantify the finity of the system.
Periodicity blocks enclose a certain number of discrete categorical intervals or pitch-classes, and the unison vectors are intervals which are small enough that pitches within the block can represent or imply pitches outside of it which have different prime or odd factors, which is related to Monzo's concept of bridging.
See also Fokker periodicity-block. For a detailed explanation, see Erlich, A Gentle Introduction to Fokker Periodicity-Blocks
Paul Erlich comments:
That's correct, but Fokker generally set the overall prime-limit (either 5 or 7) beforehand and all unison vectors connect pitches (or intervals) within this limit.
Erlich has pointed out that Monzo's concept of 'bridges' refers specifically to the kinds of prime-factors and not the numbers of prime-factors, which is what Fokker described with the periodicity block concept [see also xenharmonic-bridge].
This number of pitches in a periodicty-block can be calculated by a matrix determinant, using the prime-factors of the ratios at either ends of the bridges or unison vectors to fill the matrix.
Some observations on the history of the term:
-
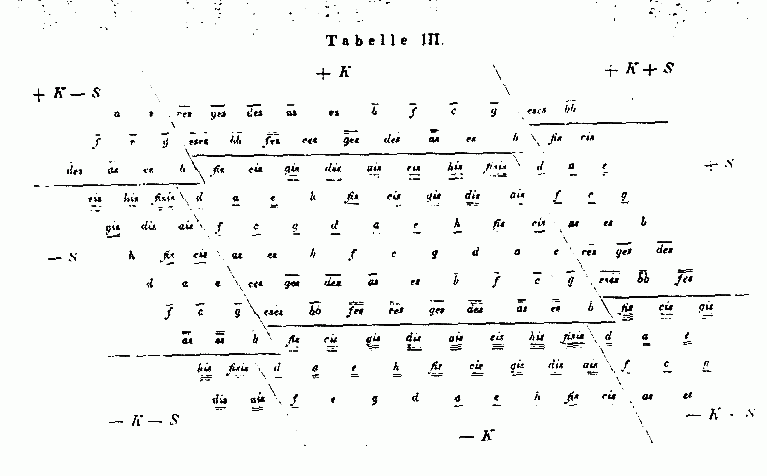
The earliest clear description of the periodicity-block concept seems to be Tanaka 1890, "Studien im Gebiete der reinen Stimmung", where Tanaka uses the kernel to show the periodic tiling of periodicity-blocks across the lattice, and calls the central periodicity-block a "tonal group" which forms a "periodic parallelogram":
Tanaka: periodic parallelogram
- Fokker 1947, Les mathématiques et la musique. Trois conférences has the term "base de périodicité"
- In Fokker 1955, >Equal Temperament and the Thirty-one-keyed Organ, Fokker mentions periodicity but then calls this a "unit cell".
- Fokker 1968, Unison Vectors and Periodicity Blocks in the Three-dimensional (3-5-7-) Harmonic Lattice of Notes.
This is Gene Ward Smith's formula for finding what he calls a "notation" for the ratios enclosed within a just intonation periodicity-block:
Where:
- M is the matrix composed of a set of i rational vectors {u1/v1, u2/v2,... ui/vi} in which u1/v1 is a step-vector and {u2/v2 ... ui/vi} are commatic or chromatic unison-vector generators of the kernel, and where
- {h1, h2, ...hi} is the top row of M^-1, and where
- round() is the function which rounds to the nearest integer,
for any non-zero a scale can be defined by calculating for 0 <= n < d : step[n] = (u1/v1)^round(h1(2)*n/d) * (u2/v2)^round(h2(2)*n/d) * ... (ui/vi)^round(hi(2)*n/d).
--- In tuning-math@y..., "genewardsmith" wrote:
> --- In tuning-math@y..., "paulerlich" wrote:
>
> > > Does "shape" entail connectedness, or can it be scattered islands
> > > all over the place?
> >
> > The latter. Especially as preimages of ETs, such constructs would be
> > just fine.
>
> Under that definition, PB <==> epimorphic. Are you sure it is the
> accepted one?
The only published articles on PBs are Fokker's. Inferring strict definitions from these articles would suggest that a parallelepiped (or N-dimensional equivalent) are the only accepted shape (thus I call these _Fokker_ periodicity blocks, or FPBs), and that if there is an even number of notes, one needs to produce two alternative versions so that symmetry about 1/1 is maintainted.
[note from Monzo: Erlich shows how to construct the parallelepiped type of periodicity-block in his A gentle introduction to Fokker periodicity blocks, part 2, and then shows that periodicity-blocks need not be parallelepipeds in his A Gentle Introduction to Fokker Periodicity Blocks: an excursion.]
... all JI scales involve a sort-of-arbitrary decision of where to stop. What I've shown is, this decision is not completely arbitrary, it almost always seems to conform to a periodicity-block construction.
Let me try graphing the 27-tone periodicity block that I posted on Thu 9/23/99 5:26 PM.
The matrix of unison vectors is
[ 3 5 7 ~cents ratio ]
2 -3 1 [ 13.79476661 126 / 125 ]
3 -1 -3 [ 13.07356932 1728 / 1715 ]
-4 3 -2 [ 13.46932519 4000 / 3969 ]
and the coordinates are
[ 3 5 7 ~cents ]
-3 2 -2 329
-2 1 -2 645
-2 1 -1 414
-2 2 -3 62
-1 0 -2 960
-1 0 -1 729
-1 1 -3 378
-1 1 -2 147
0 -1 -1 1045
0 -1 0 814
0 0 -3 694
0 0 -2 462
0 0 -1 231
0 0 0 0
0 1 -4 111
1 -2 0 1129
1 -1 -3 1009
1 -1 -2 778
1 -1 -1 547
1 0 -3 195
2 -2 -2 1094
2 -2 -1 862
2 -1 -3 511
2 -1 -2 280
3 -3 -1 1178
3 -2 -2 596
4 -3 -2 911
I think I'll go back to the usual orientation for this one:
5
/:\
/ : \
/ 7 \
/,' `.\
1---------3
And we're off:
329
\`.
\ 62
\ : 414
\: ,' `.
645-------147
\`. ,'/:\ 0
\ 378 / : \ ,'/
\ : /.729-------231 /
\:/,'**\`.\ ,'/:\/
960-------462 / :/\
`. : ,' : / 814 \
694--\:/,'195`.\
\ 1045-/:\--547
\ `/ : \' : `.
\ / 778-\-----280
\ /.' \`.\@@,'/:\
1009------511 / : \
\ : / 862 \
\:/,' `.\
1094------596
:\
: \
1178\
`.\
911
**111 goes here, but there was not enough room to write it.
@@1129 goes here, but there was not enough room to write it.
This one is amazingly rich in 7-limit triads and tetrads, so much so that it's straining my meager ASCII symbology to show all the connections.
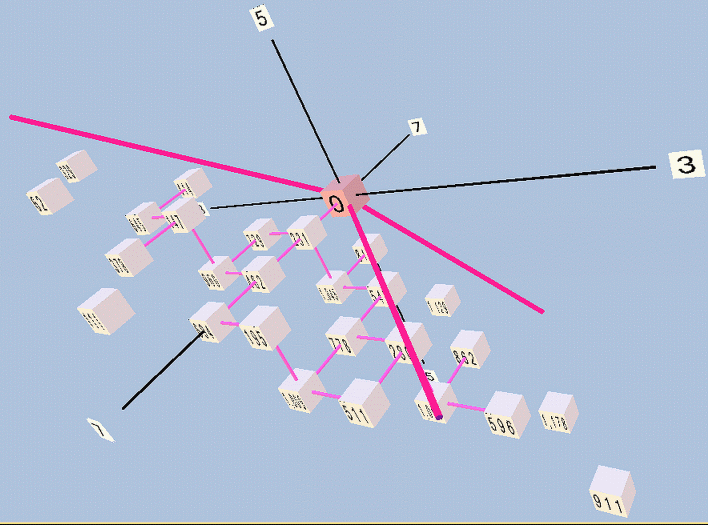
[from Monzo:] Below are some views of TonescapeTM lattice-diagrams of Erlich's 27-tone periodicity-block. First, a triangular lattice exactly like the one Erlich drew in ASCII:
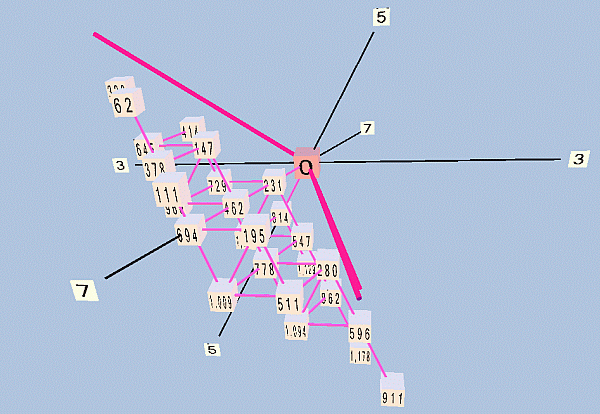
Next, the same but in rectangular format:
These three basic scales, identified in my paper as the melodic bases for 3-, 5-, and 7-limit harmony, respectively, have JI representations that come out as Fokker periodicity blocks when the typical "chromatic" interval implied by the scales is used as a unison vector.
Interestingly, all these periodicity blocks are of the "most natural" type catalogued by Kees van Prooijen (he skipped the 3-limit ones but they're trivial -- apparantly not enough so to satisfy Carl [Lumma]?)
In the 3-limit pentatonic case, modulating the scale by a single ratio of 3 simply moves one note by 256:243. Using this as the unison vector (only one is needed since octave-equivalent 3-limit space is one-dimensional), we get the following periodicity block:
ratios for major 1/1-------3/2-------9/8------27/16-----81/64 ratios for minor 32/27-----16/9-------4/3-------1/1-------3/2
Interestingly, as I was writing this, Carl [Lumma] posted something about 1D periodicity blocks, to which this may relate.
In the 5-limit diatonic case, 81:80 is already assumed as a unison vector, and the chromatic interval by which one note moves when modulating by a ratio of 3 is 25:24. Using these as the unison vectors, the resulting periodicity block is:
ratios for major
5/3-------5/4------15/8
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
4/3-------1/1-------3/2-------9/8
or
10/9-------5/3-------5/4------15/8
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
4/3-------1/1-------3/2
or
100/81-----50/27
\ / \
\ / \
\ / \
\ / \
40/27-----10/9-------5/3
\ / \
\ / \
\ / \
\ / \
4/3--------1/1
ratios for minor
1/1-------3/2-------9/8
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
8/5-------6/5-------9/5------27/20
or
4/3-------1/1-------3/2-------9/8
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
8/5-------6/5-------9/5
or
40/27-----10/9
\ / \
\ / \
\ / \
\ / \
16/9-------4/3-------1/1
\ / \
\ / \
\ / \
\ / \
8/5--------6/5
[from Monzo:] Below is one view of a TonescapeTM triangular lattice of the same type of periodicity-block:
periodicity-block, 3,5-prime-space, 7-tone, TonescapeTM triangular lattice
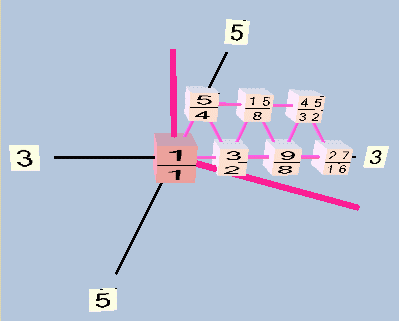
In the 7-limit decatonic case, 64:63 and 50:49 are already assumed as unison vectors. If you are unfamiliar with decatonic scales, see my paper. When modulating by a 3-limit ratio, two notes move by a 48:49. Using these as the unison vectors, the resulting periodicity block is:
ratios for symmetrical major
5/4------15/8 7/4------21/16
,'/:\`. ,'/:\`. ,'/:\`. ,'/:\`.
10/7-/-:-\15/14/-:-\45/28 or 1/1-/-:-\-3/2-/-:-\-9/8
: / 7/4------21/16\ : : /49/40----147/80\ :
:/,' `.\:/,' `.\: :/,' `.\:/,' `.\:
1/1-------3/2-------9/8 7/5------21/20-----63/40
or
16/9-------4/3-------1/1 80/63-----40/21-----10/7
:\`. ,'/:\`. ,'/: :\`. ,'/:\`. ,'/:
: \32/21/-:-\-8/7 / : : 160/147-:-\80/49/ :
56/45-----28/15------7/5 or 16/9-------4/3-------1/1
`.\:/,' `.\:/,' `.\:/,' `.\:/,'
16/15------8/5 32/21------8/7
or
5/4 7/4
.'/:\`. .'/:\`.
40/21-----10/7-/-:-\15/14 4/3-------1/1-/---\-3/2
:\`. ,'/: / 7/4 \ : :\`. ,'/: /49/40\ :
: \80/49/ :/,' `.\: or : \ 8/7 / :/.' `.\:
4/3-------1/1-------3/2 28/15------7/5------21/20
`.\:/,' `.\:/,'
8/7 8/5
ratios for symmetrical minor
4/3-------1/1 40/21-----10/7
,'/:\`. ,'/:\`. ,'/:\`. ,'/:\`.
32/21/-:-\-8/7-/-:-\12/7 or 160/147/-:-\80/49/-:-\60/49
: /28/15------7/5 \ : : / 4/3-----/-1/1 \ :
:/,' `.\:/,' `.\: :/,' `.\:/,' `.\:
16/15------8/5-------6/5 32/21------8/7------12/7
or
40/21-----10/7------15/14 4/3-------1/1-------3/2
:\`. ,'/:\`. ,'/: :\`. ,'/:\`. ,'/:
: \80/49/-:-\60/49/ : : \ 8/7-/-:-\12/7 / :
4/3-------1/1-------3/2 or 28/15------7/5------21/20
`.\:/,' `.\:/,' `.\:/,' `.\:/,'
8/7------12/7 8/5-------6/5
or
21/16 15/8
.'/:\`. .'/:\`.
1/1-------3/2-/-:-\-9/8 10/7------15/14/---\45/28
:\`. ,'/: 147/80\ : :\`. ,'/: /21/16\ :
: \12/7 / :/,' `.\: or : \60/49/ :/.' `.\:
7/5------21/20-----63/40 1/1-------3/2-------9/8
`.\:/,' `.\:/,'
6/5 12/7
[from Monzo:] Below is one view of a TonescapeTM triangular lattice of the same type of periodicity-block:
periodicity-block, 3,5,7-prime-space, 10-tone, TonescapeTM triangular lattice
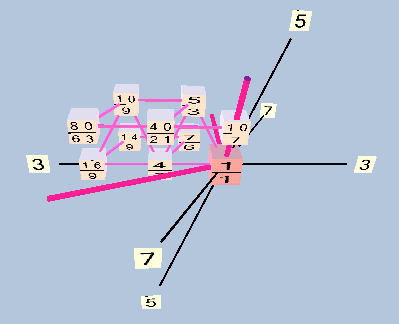
I don't think the pentachordal decatonic scales can be thought of as periodicity blocks, but I could be wrong . . .
See also:
Erlich, Paul and Monzo, Joe. 1999. The Indian Sruti System as a Periodicity-Block
Erlich, Paul. 1999. Partch's 43-tone Scale as a Periodicity-Block
Please help keep Tonalsoft online! Select your level of support from the menu. Thank you!
