[from Joe Monzo, JustMusic: A New Harmony, with help from Paul Erlich]
A translation of a set of coordinates from one vector-space into another.
Transformations become important in tuning theory because many theorists (like myself) employ tonal lattice diagrams to portray the frequency relationships between pitches, and transformations describe the manipulations of coordinates between different axes on the lattice, which represent different scales and tuning systems or different dimensions within one multi-dimensional system.
I will explain here the mathematics of doing a 2-dimensional transformation. Working in higher-dimensional spaces, one utilizes what are essentially the same procedures, but they are more complicated because of the additional dimensions.
Let (x,y) be the unit-vectors which define and generate a 2-dimensional vector-space, so that
x = 1,0 y = 0,1
Let (i,j) be another set of coordinates, which may be used to define and generate a different 2-dimensional space, such that
i = ax + by j = cx + dy
This set of equations can be rewritten using matrices as follows:
[i] [a b] [x] [ ] = [ ]*[ ] [j] [c d] [y]
Now that we know how the new space relates to the old one with which we are already familiar, we want to find the opposite: how the old space is seen in the perspective of the new one. In other words, we know what i and j are in terms of the unit-vectors x and y, but what are x and y when the unit-vectors are i and j?
So we must solve for x and y. This can be done by "dividing both sides" by the matrix, or technically, inverting the matrix. The formula for the inverse of a two-by-two matrix
[a b] [ ] [c d]
is
1 [ d -b] --- * [ ] n [-c a]
where
n (the determinant) = a*d - b*c.
This operation yields
[x] [ d/n -b/n] [i] [ ] = [ ]*[ ] [y] [-c/n a/n] [j]
or in algebriac terms,
x = (di - bj) / n y = (aj - ci) / n
As an example, I will illustrate an example given in Regener 1973. I posted Richard Chrisman's Journal of Music Theory review of Regerner's book in Yahoo Tuning message 14995 ( Tue Oct 24, 2000 1:34am).
This is the example which reinterprets coordinates (d,q) in terms of units (a,b) in interval space I, into coordinates (a,b) in the new unit terms (d,q) of interval space K0. So,
(Regener's (d,q) are equivalent to the (i,j) in my definition above, and his (a,b) are equivalent to the (x,y) in my definition. We'll fill in my definition's matrix variables a,b,c,d with actual numbers.)
Let's start with a graph plotting a(1,0) + b(0,1) in space I (click on graphic to open larger view):
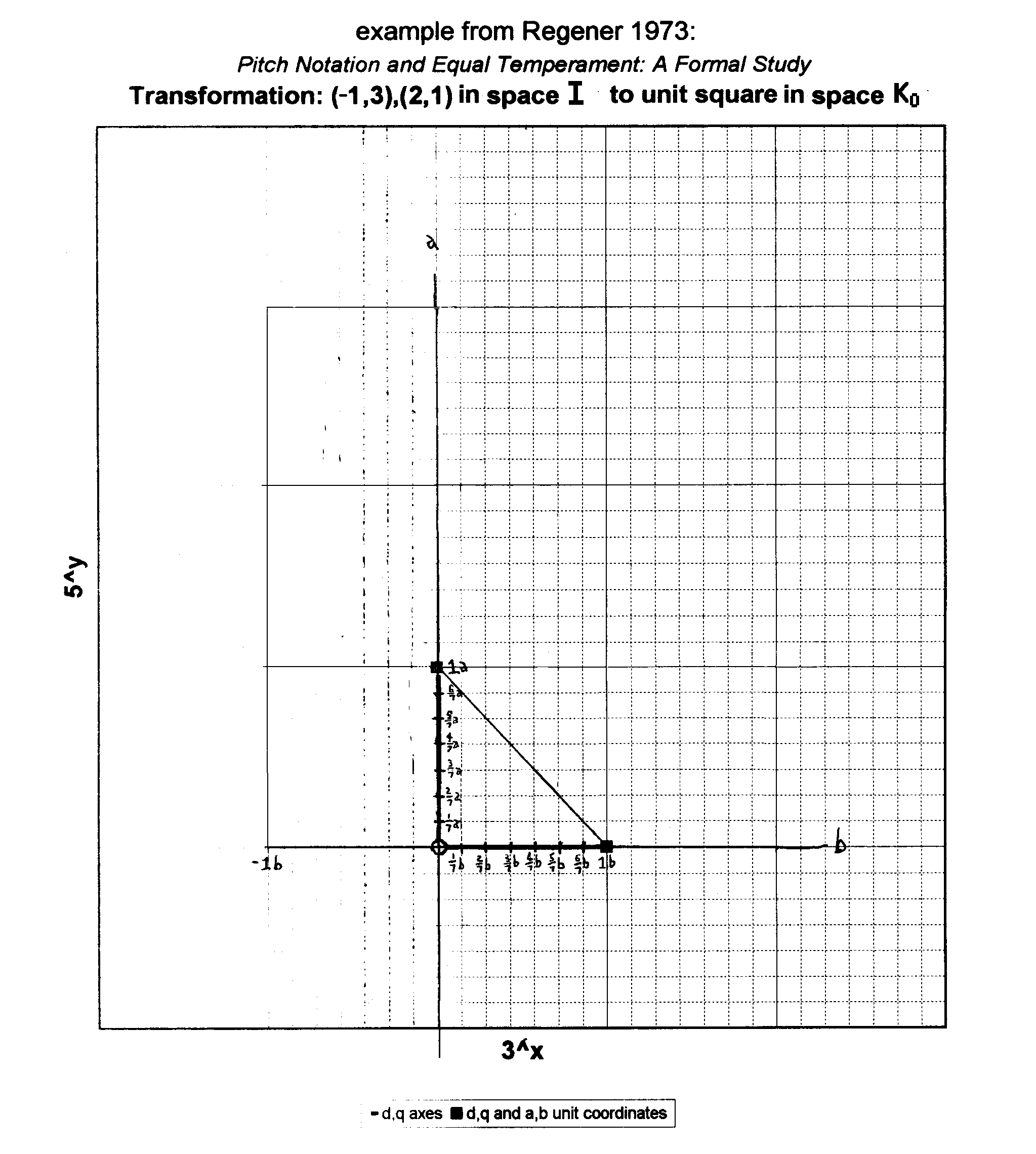
(There's a reason why each side of the unit-square here is divided into 7 parts. It will become clear later.)
Next we plot the two points which define the corners of the unit-square in our new space; Regener calls them d,q (which stand for his words "diatone" and "quint", which respectively describe the vertical and horizontal axes of his interval space I). These two pairs of coordinates define the generating intervals or generators of our new space, which Regener calls K0.
In terms of (a,b) in space I, the two new generating intervals in Regener's example have the coordinates d = (3,-1) and q = (1,2):
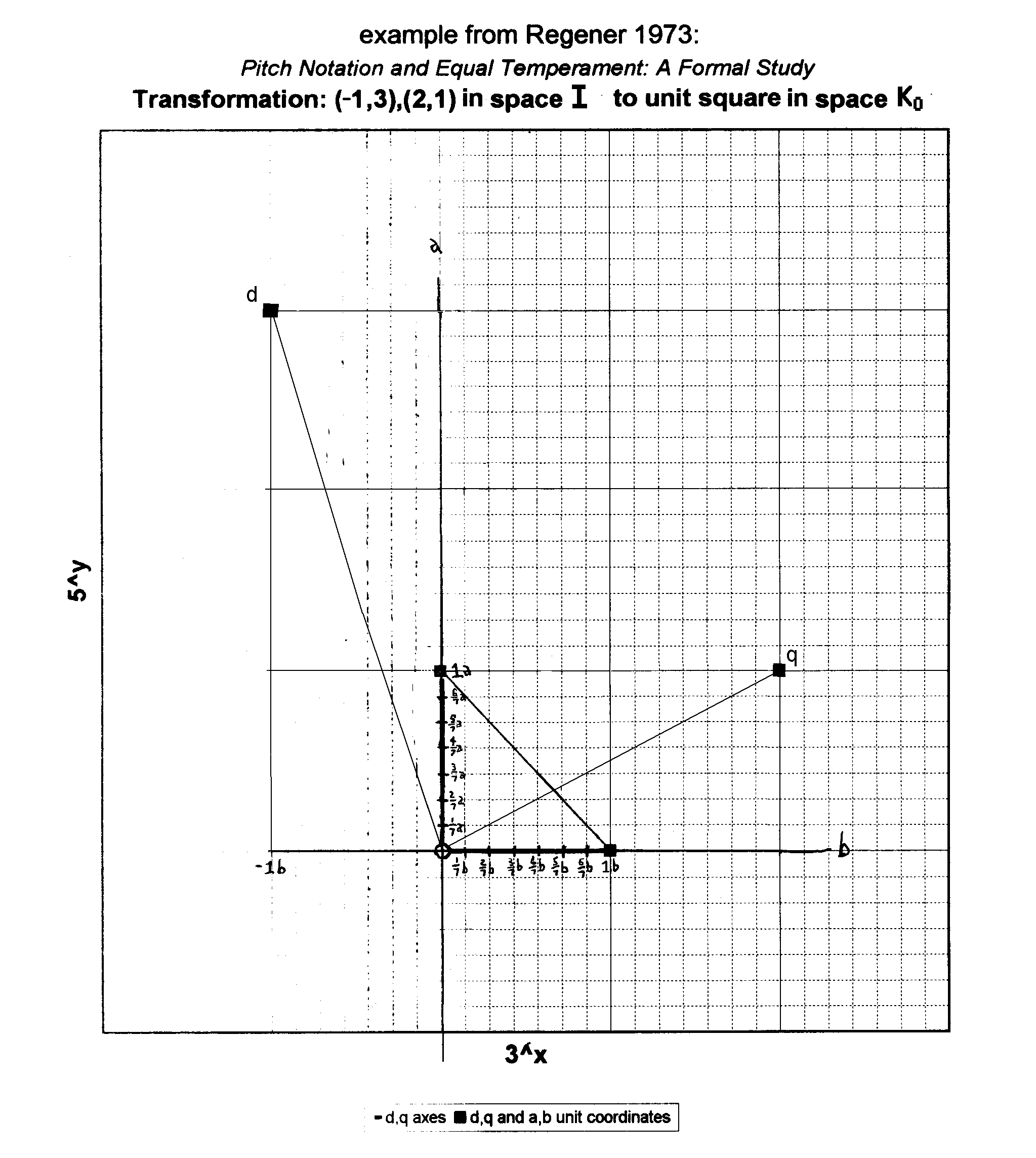
In algebraic terms:
in space I, d = 3a - b q = a + 2b.
This can be derived algebraically as follows:
d(1,0) + q(0,1) = a(3,1) + b(-1,2) so
(d,q) = (3a-b,a+2b) and
d = 3a - b
q = a + 2b
Now that we know what d and q are in terms of the unit-vector values a and b in space I, we can find the reciprocal relationship, and determine what a and b are in terms of unit-vector values d and q in space K0.
Paul Erlich, Yahoo Tuning message 15059 (Wed Oct 25, 2000 4:11pm), showed how to solve for a and b both algebraically and by using matrices. The original equation I posted was wrong, so I've adapted Paul's post to be correct here, and expanded the explanation in a few place to clarify:
You can solve this system of equations by first multiplying
the second equation by -3:
q = a + 2b
* -3
---------------
-3q = 3a - 6b
and then adding the other equation
-3q = 3a - 6b
+ d = 3a - b
----------------------
= -3q+d = - 7b
Multiply that by -1 to get 3q-d = 7b.
So b = (3q - d) / 7.
Now plug that back into either equation to solve for a.
Using the first equation
d = 3a - b
we find
d = 3a - ( (3q-d) / 7 )
add ( (3q-d) / 7 ) to each side:
d + ( (3q-d) / 7 ) = 3a
express d as a multiple of the denominator,
to make d part of the numerator:
(7d+3q-d) / 7 = 3a
simplify the numerator:
(6d + 3q) / 7 = 3a
divide by 3:
(2d + q) / 7 = a.
Another way to solve this is using matrix inversion.
The original system of equations can be written:
[d] [3 -1] [a]
[ ] = [ ] * [ ]
[q] [1 2] [b]
This can be solved by "dividing both sides" by the matrix, or technically,
inverting the matrix. The formula for the inverse of a two-by-two matrix
[a b]
[ ]
[c d]
is
1 [ d -b]
--- * [ ]
det [-c a]
where
det = a*d - b*c.
This operation yields
[a] [ 2 1] [d]
[ ] = [ ]*[ ]
[b] [-1 3] [q]
-------
7
which equals
[a] [ 2/7 1/7] [d]
[ ] = [ ]*[ ]
[b] [-1/7 3/7] [q]
Thus,
a = (( 2/7) * d) + ((1/7) * q)
b = ((-1/7) * d) + ((3/7) * q)
or in simplified terms
a = (2d + q) / 7
b = (-d + 3q) / 7
|
It's easy to see on the last diagram (below) that a and b can be located in terms of 1/7ths of d and q in space K0 by these equations. Therefore,
In space I,
a = (1, 0)
b = (0, 1)
d = (3,-1)
q = (1, 2)
In space K0,
d = ( 1,0 )
q = ( 0,1 )
a = ( 2/7,1/7)
b = (-1/7,3/7)
Here's the graph I made which shows the relationship: (click on the graphic to open a larger version)
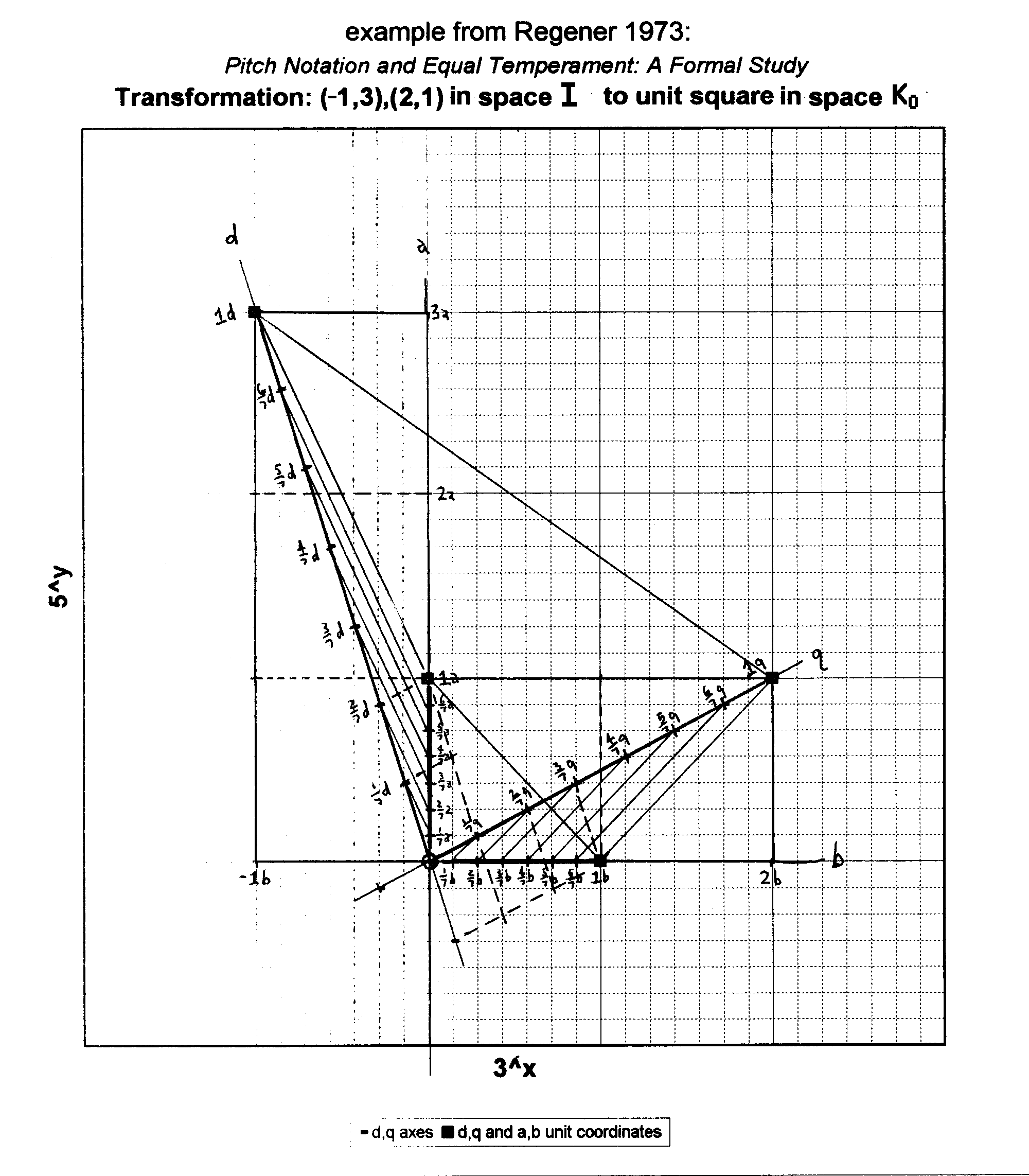
The reason why the original unit-square of space I was shown divided into 7 parts, is that 7 happens to be the determinant of this particular matrix, and so thus it is the smallest number which exactly divides the unit-squares of both interval spaces I and K0, and therefore it is the smallest denominator fractional part which gives integer values for the numerators when the units of the two spaces are compared to each other.
Paul Erlich makes use of 3-dimensional transformations in his A Gentle Introduction to Fokker Periodicity Blocks, part 3. In calculating a periodicity-block, the unison-vectors form the unit-vectors of a space.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.