One of several small intervals with a size of about an eighth-tone [= 0.25 Semitone = 25 cents]. They occur in a system of just-intonation, or when considering intervals as ratios.
The three commas which are most commonly encountered are the syntonic comma, the pythagorean comma, and the septimal comma.
When used unqualified, "comma" generally refers specifically to the syntonic comma.
(Greek: "cut", "crack"; plural: commata)
Any of several small intervals near an eighth of a tone (25¢). The best known of these are the Syntonic Comma, the pythagorean Comma (24¢) which is the difference between twelve Perfect Fifths and seven Octaves, and the Septimal Comma (27¢).
From: Dave Keenan
Date: Sat Feb 8, 2003 7:42 pm
Subject: That poor overloaded word "comma"
[much snipped ...]
At least now the word "comma" only has to carry two meanings, where one is a generalisation of the other. Here's my suggestion.
A difference between pitch ratios that is typically smaller than a scale step. May include schismas, kleismas, commas (2), dieses, limmas and small semitones [thus, in the range from imperceptibly small to around 125 cents].
A difference between pitch ratios that is typically in the range 12 to 33 cents, as opposed to schismas and kleismas being smaller, and dieses, limmas and small semitones being larger.
[The following paragraph and graph added by Monzo.]
The graph below shows an approximate range for this second definition of "comma", with other categories of small intervals also named. Keenan's first definition of "comma", above, covers all the interval categories on this graph.
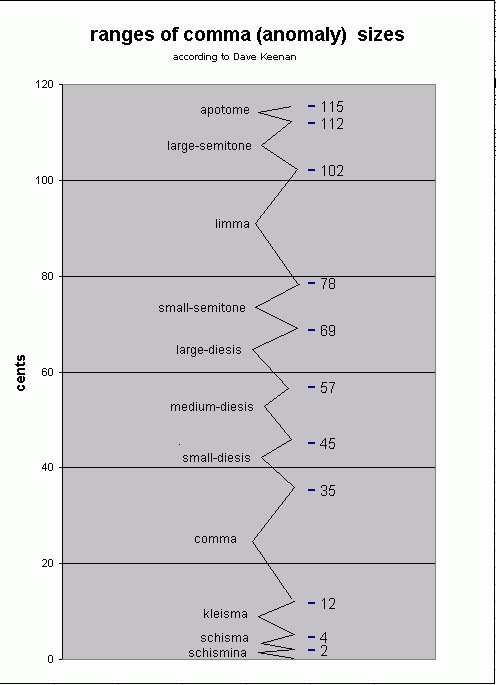
Below is the data for the comma category cutoffs which George Secor and Dave Keenan found most useful while developing sagittal notation. The boundaries occur at the square roots of the given ratios, which is why the cent values are half.
Square of boundary Boundary Name
2,3-monzo ratio ~cents
[-106 67, > (numbers too big) 115.492529
> apotome
[ 62 -39, > (numbers too big) 111.8774831
> large-semitone
[ -3 2, > 9 / 8 101.9550009
> limma
[ -49 31, > (numbers too big) 80.30251341
> small-semitone
[ -30 19, > 1073741824 / 1162261467 68.57250822
> large-diesis
[ -11 7, > 2187 / 2048 56.84250303
> (medium-)diesis
[ 8 -5, > 256 / 243 45.11249784
> small-diesis
[ 27 -17, > 134217728 / 129140163 33.38249264
> comma
[ -19 12, > 531441 / 524288 11.73000519
> kleisma
[ 317 -200, > (numbers too big) 4.499913461
> schisma
[ -84 53, > (numbers too big) 1.807522933
> schismina
[ 0 0, > 1 / 1 0
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.