One of the basic intervals (along with the tone) of every diatonic scale. In several different theories of the medieval, Renaissance, Baroque, and Classical periods, a distinction was made between chromatic and diatonic semitones, as there were two different sizes of semitone in many tuning systems. (Two good examples are pythagorean and meantone.)
The diatonic semitone is the interval between two notes of a diatonic scale which have different letter-name nominals, whether or not one of them is qualified by an accidental, as in B:C or A:Bb. The implication is that both notes are bonafide diatonic scale-degrees. The standard interval name is "minor-2nd" and may be found abbreviated as min2, m2, b2, or -2, and it is also called the diatonic-semitone.
In the pythagorean [3-limit] system, the diatonic semitone is also called the leimma or limma. The standard pythagorean diatonic A-minor scale, which was a medieval version of the ancient Greek GPS, has the following ratios, arranged here as a chain-of-5ths -- that is, exponents of 3 -- and the equivalence-interval 2 is not shown:
128/81 32/27 16/9 4/3 1/1 3/2 9/8 -4 -3 -2 -1 0 1 2 = 3x
The same tuning system is shown below arranged from left to right in ascending order of pitch, i.e., as an actual scale, with the equivalence-interval (2/1 ratio) included at the end:
1/1 9/8 32/27 4/3 3/2 128/81 16/9 2/1 0 2 -3 -1 1 -4 -2 0 = 3x
The diatonic semitone in this scale is the ratio 256:243 = 283-5 = 2,3-monzo [8 -5> = ~90.22499567 cents. It occurs in this scale between the pairs of ratios ( 81/64 : 4/3 ) and ( 243/128 : 1/1 ) ; as an example, if we call the 1/1 "C", the diatonic-semitone occurs between the pairs of notes E:F and B:C :
diatonic diatonic
semitone semitone
+-------+ +------+
| | | |
1/1 9/8 32/27 4/3 3/2 128/81 16/9 2/1
0 2 -3 -1 1 -4 -2 0 = 3x
A B C D E F G A
The 5-limit JI diatonic scale has the following ratios, shown here on a 2-dimensional lattice-diagram where 2 is the equivalence-interval (not shown), exponents of 3 form the horizontal axes, and exponents of 5 form the vertical axes, the 3,5-monzo is shown below the ratio, and letters are added to identify the notes as the C-major scale:
5/3 ---- 5/4 --- 15/8 [-1,1> [0,1> [1,1> A E B | | | | | | 4/3 ---- 1/1 ---- 3/2 ---- 9/8 [-1,0> [0,0> [1,0> [2,0> F C G D
The same tuning-system is shown below in ascending order of pitch, i.e., as an actual scale, with the equivalence-interval added at the end:
1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1 [0,0> [2,0> [0,1> [-1,0> [1,0> [-1,1> [1,1> [0,0> C D E F G A B C
The diatonic semitone in this scale is the ratio 16:15 = 243-15-1 = 2,3,5-monzo [4 -1, -1> = ~111.7312853 cents. It occurs in this scale between the pairs of ratios ( 5/4 : 4/3 ) and ( 15/8 : 1/1 ) ; as an example, if we call the 1/1 "C", the diatonic-semitone occurs between the pairs of notes E:F and B:C :
diatonic diatonic
semitone semitone
+-----+ +----+
| | | |
1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1
C D E F G A B C
Meantone tunings are also chain-of-5th tunings, therefore, in a meantone tuning, the diatonic semitone is technically -5 generators, exactly as in pythagorean tuning. Here are the sizes of the diatonic semitone in various historical meantone tunings:
meantone equivalent EDO-meantone
~cents ~cents
1/3-comma 126.0688117 2(2/19) 126.3157895
LucyTuning 122.5351707 2(9/88) 122.7272727
2/7-comma 120.9482665 2(5/50) 120.0
7/26-comma 119.1757701 2(5/50) 120.0
golden 118.9276302 2(8/81) 118.5185185
1/4-comma 117.1078577 2(3/31) 116.1290323
2/9-comma 114.120873 2(7/74) 113.5135135
1/5-comma 111.7312853 2(4/43) 111.627907
1/6-comma 108.1469037 2(5/55) 109.0909091
1/11-comma 100.0005819 ~= 2(1/12) 100.0
The EDO versions of these tunings in this context should properly be called ETs, because they are equal-temperaments -- that is, tunings which are tempered approximations of 5-limit JI; they are shown on the graph below. (Note that 81-edo is closer to Woolhouse's 7/26-comma meantone than 50-edo, but Woolhouse specificially outlined 50-edo as an approximation to 7/26-comma.)
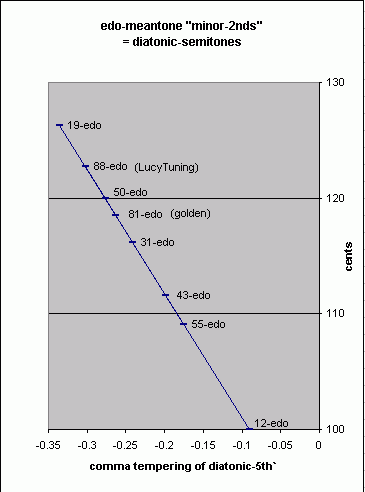
As can be seen from a comparison of this graph with that for the chromatic-semitone, the variation of the diatonic-semitone is over a narrower range than that of the chromatic-semitone.
Note that in positive systems (typical example: Pythagorean tuning), the chromatic semitone is larger than the diatonic, while in negative systems (typical example: any tuning of the meantone family) it is exactly the opposite and the diatonic is the larger.
Marchetto specified three types of semitone: diatonic, enharmonic, and chromatic; however, his names were matched with the intervals differently than in traditional theory.
Note also that the miracle generator, the secor (~116.7 cents), is also in the typical size range of a diatonic semitone, but it may not necessarily function as one.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.