Iranian segah mode
In tuning@yahoogroups.com, "monz" wrote:
In tuning@yahoogroups.com, "Mohajeri Shahin" wrote:
Dear friends
I calculated these intervals of the first tetrachord of "SEGAH" mode played by maestro ebadi (an Iranian traditional music master) by digital tuner. What is your opinions?
Fa ........ 0 cent Sol ..... +15 cent La b ... +56 cent ( an interval called LA KORON) Si b ..... +1.57 cent Do ....... +9.5 centSori and koron are (1/4 tone - interval) of Iranian music but never tuned to 50 cent.
hmmm ... fa:do (F:C) is not a tetrachord, it's a pentachord. anyway, to be clear, is this exactly what you mean? ...
.............. ------ cents ------- Do .... C ... 700 + 9.5 = ... 709.5 Si b .. Bb .. 500 + 1.57 = .. 501.57 La b .. Ab .. 300 + 56 = .... 356 Sol ... G ... 200 + 15 = .... 215 Fa .... F ..... 0 .... = ...... 0
The proportion of this pentachord is roughly 30 : 34 : 37 : 40 : 45 . i.e., this is the set of smallest numbers which give a good approximation of the integers in the "ideal" JI proportion of the pentachord.
More exact figures for Mohajeri's cents values are: 30 : 33.96689085 : 36.84909448 : 40.08152779 : 45.19654528 .
To create the lattice, we use the integer approximations and divide all numbers by 30 to make that note the 1/1:
30/30 : 34/30 : 37/30 : 40/30 : 45/30 = 1/1 : 17/15 : 37/30 : 4/3 : 3/2
Then, prime-factor the numbers and write the exponents of the prime-factors (in order of the prime-series) as a monzo, thus:
2 3, 5 7 11, 13 17 19, 23 29 31, 37 -monzo [-1 1, > (3/2) [ 2 -1, > (4/3) [-1 -1, -1 0 0, 0 0 0, 0 0 0, 1 > (37/30) [ 0 -1, -1 0 0, 0 1 > (17/15) [ 0 > (1/1)
Usually i like to end the monzo at the prime-limit of that ratio, as i did above. but in illustrating vector calculations it's more helpful to make all of them the same length.
Since this pentachord makes use of the two higher primes 17 and 37, but otherwise is 5-limit, there are a lot of useless zeros in the monzos, so in this case it's better to use comma-marks after every number and show only the exponent for primes which are <>0 , and explicitly tell which primes *are* being used. so this pentachord notated that way is:
2,3,5,17,37-monzo [ -1, 1, 0, 0, 0 > (3/2) [ 2, -1, 0, 0, 0 > (4/3) [ -1, -1, -1, 0, 1 > (37/30) [ 0, -1, -1, 1, 0 > (17/15) [ 0, 0, 0, 0, 0 > (1/1)
This matrix of monzos is virtually a lattice already.
Assuming octave-equivalence (i.e., ignoring prime-factor 2), here's the lattice that the Musica software drew for it:
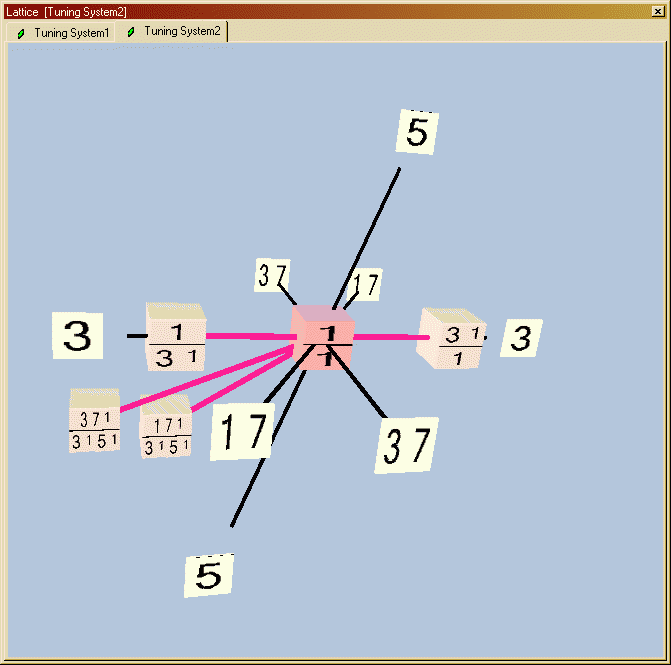
Note that because >3 dimensions are shown, the arrangement of the axes is somewhat arbitrary.
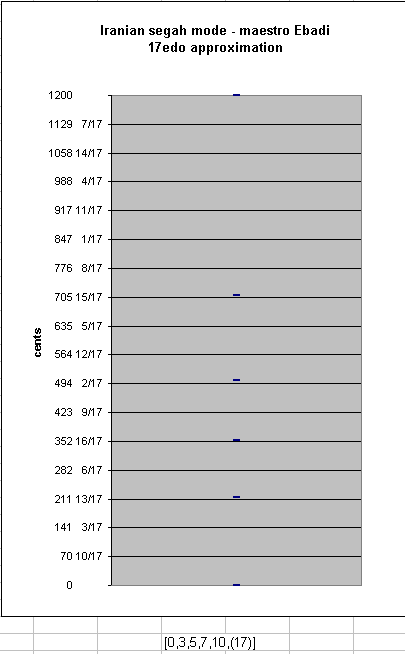
Among equal-temperaments with cardinality below an arbitrary cutoff point of 54, Ebadi's segah is approximated best by 17-edo, and a little less well by 24-edo. The smallest cardinality which offers anything resembling Ebadi's segah is 10-edo. The familiar 12-edo is unable to map the koron, and is only shown here for comparison. (mouse over the links to see the graphs)
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
