Speculations on Marchetto of Padua's "Fifth-Tones"
DISCLAIMER: The ratios deduced in this examination are pure speculation. There is no evidence known by the author which proves that his claims are correct, however, it is hoped that the logic of these assertions proves compelling enough to stimulate further research and debate on this subject.
Marchetto of Padua's Lucidarium1;,
written around 1318,
describes a way of dividing the "whole tone" into 5 parts. This
has been taken by Jan Herlinger to mean a division of the 9:8
"whole tone" into 5 equal
parts, each part having an interval size of approximately
0.41 Semitones
[= (9/8)(1/5) = ~40.782
cents]
and this view has become widely accepted. 2
In a confusing passage of Marchetto's book I think I have found evidence that this approach is incorrect, and that Marchetto's system was actually much more mathematically elaborate and ingenious.
The Lucidarium is divided into 16 short treatises: the first one introductory, the second one describing his unique divisions, and the rest going on to describe proportions and ratios, consonances, chromatic alteration thru mutation (he calls it 'permutation'), and modes.
Marchetto begins with the statement that the focus will be on plainchant, and not 'measured music' (i.e., that which has a written, or measured, rhythm). He goes on to give definitions of music and some of its broader aspects and subdivisions, and he invokes Pythagoras twice, as well as such other music-theory luminaries of the past as Remigius, Bernard, Boethius, and Guido, in support of his definitions - all of which is typical at the beginning of the medieval music-theory treatise. He then ends Treatise 1 with the statement that
| Et quia de dictis cromatico, dyatonico, et enarmonico non posset plene tractari nisi de tono prius videretur, cum ipsa sint semitonia, iccirco primo videndum est quid sit tonus et quomodo per numeros dividatur. 3 |
| Because the aforesaid chromatic, diatonic, and enharmonic [species] cannot be fully treated until the whole tone is examined (since they are semitones), we shall first study the nature of the whole tone and how it is divided by numbers. |
Our entire focus here will be on what follows in Treatise 2. 4
Marchetto refers to his "fifth-tone" as a diesis, a term used in ancient Greek theory to designate a number of different small intervals. He specifies in his theory that there are three sizes of "semitone" rather than the usually-accepted two, and gives the names and the number of dieses contained in each. In the concluding chapters of the second treatise he describes the ratios for two of the "semitones", as well as for the "tone". We may tabulate these measurements as follows: 5:
| Type of interval | Size in dieses | Ratio | Semitones | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| whole tone | | 9/8 | chromatic semitone | -- | diatonic semitone | 17/16 | enharmonic semitone | 18/17 | |
Returning to the beginning of Treatise 2, Marchetto discusses the various names Greek and Latin theorists had given to the 'whole tone' (epogdous, diastema, emmele, colon, sesquioctava), introducing the concept of the 8:9 ratio here in connection with the synonomous names (epogdous and sesquioctava).
Next comes the major subject matter of our present work, introduced by Chapter 4 of Treatise 2, entitled In quibus numeris constituatur tonus ['the numbers in which the whole tone is to be constituted'], where Marchetto claims to be the first person to explain why the whole tone has the proportion 8:9 :
|
Sciendum est quod, secundum omnes auctores musica, tonus, sive natura eius, dicitur
consistere in proportione novenarii numberi ad octonarium.
Qua ratione autem hoc sit nundum invenitur fuisse ab auctoribus demonstratum.
Hoc autem demonstrare intendimus, circa quod hoc ordine procedemus: Primo enim ostendemus qua ratione tonus consistat in novenario numero et non in maiori numero vel minori. Secundo per hoc ostendemus quomodo tonus se habeat ad octonarium numerum. Tercio ex hiis concludetur quod natura toni consistit in proportione numeri novenarii ad octonarium et non in aliorum proportionibus numerorum. 6 |
|
It must be known that, according to all writers on music,
the whole tone - or its nature
- is said to consist in the proportion of the number nine to the
number eight. Why this should be so has not yet been found demonstrated
by those writers.
We intend to prove it, and to do so we shall proceed in this order: First we shall show why the whole tone consists in the number 9 and not in a larger number or a smaller one. Second we shall show, by means of this, how the whole tone is related to the number 8. Third we shall draw from these the conclusion that the nature of the whole tone consists in the proportion of the number 9 to the number 8 and not in the proportions of other numbers. |
The first point (whole tone = 9) is given a detailed explanation, then the second point (relation to 8) is described briefly enough that the third point is combined with it. It is worth noting that Marchetto makes a distinction between saying that 'the whole tone [itself] consists in the number 9' and 'the nature of the whole tone consists in the proportion of 9 to 8'.
Marchetto begins with abstract theory. Note that his metaphysical basis is the same as the one postulated by Aristoxenus: a continuum of pitch from lowest to highest. It is important to emphasize this point because both Aristoxenus and Marchetto were interested in finding more subtle divisions of the whole-tone than those that had been described by other theorists.
| Quantum ad primum, est sciendum quod, secudum omnes phylosophos et doctores in istis materialibus, numerus causatur ex divisione continui; et in tot partes in quot potest dividi continuum, et eo modo quo potest dividi, tot possunt esse numeri, et eodem modo etiam augmentari; propter quod ipsi dicunt quod quia continuum est divisible in infinitum, ideo numerus est augmentabilis in infinitum. 7 |
| First, according to all philosophers and doctors in these matters, number has as its cause the division of a continuum. Into however many parts the continuum can be divided, so many numbers can there be; and they can be augmented in the same way it can be divided. |
Then he gets down to particulars; Herlinger, however, notes several textual variations and erasures in the manuscripts of the first sentence here, apparently indicating that it was misunderstood by later scribes:
| Nunc autem sic est, quod continuum ultimiori divisione in qua possit dividi, si omnem divisionem comprehendere volumus ita ut non reducatur, est ipsius divisio in tres partes, 8 |
| Now if we wish to embrace every division, [the manner] in which the continuum can be divided with the ultimate division so that it is not reduced, is its division into three parts. |
I think this translation could be expressed more clearly also. I would render it more literally as:
| Now but it is so, that the furthest division into which the continuum may be divided, if we wish to embrace every division so that it may not be reduced, is its division into 3 parts. |
He sees any division as being reducible into ultimately either 2 or 3, because all other numbers can be derived from these two, either by addition or multiplication:
|
nam si divideremus primo ipsum in quatuor, esset ipsum dividere in bis duas;
si in quinque, in tres et duas; si in sex, in bis tres; et cetera;
et sic, tales divisiones non essent primem, sed ad alias reducerentur.
Si autem ipsum continuum divideremus in duas, illas non esset ipsius prima maior divisio, cum plus contineat ipsius divisio in tres. Sic ergo patet quod continuum, primo et de se primaria et maiori divisione, divisibile est in tres partes. 1g |
|
for if we were to divide it first into 4,
that would itself be divided into twice 2; if into 5,
into 3 and 2; if into 6, into twice 3; etc.;
and thus, such divisions would not be prime, but would
be reducible to another.
But if we were to divide the continuum into 2, that would not be its major prime division, since it would contain more divisions of itself [if divided] in 3. Thus therefore it is manifest that the continuum, the first and of itself the primary and greater division, is divisible into 3 parts. |
Marchetto goes thru an elaborate explanation of how an odd number cannot be evenly divided, since 3 is odd. He uses his example, multiplying 3 by itself repeatedly, to get the series 3, 6, 9, 27. Thus, these larger numbers can be divided repeatedly by 3, but not by 2. Then he explains how the divisions of these numbers works inversely to the multiplication which produced them. He, or a later scribe, even provides diagrams to illustrate the math9; as is usual in medieval European music-theory manuscripts, the deceptively "obvious" visual "aids" serve more to further obfuscate the text than to clarify it.
Then he goes thru the same procedure to show how 2 can be multiplied by 2 over and over again to produce larger numbers such as 4, 8, 16, etc., and how the divisions are identically proportional.
It is worth examining this section in more detail, as I believe it has a direct bearing on the ratios in Marchetto system.
So far so good. Now things get sticky...
In the passage I have referred to above as confusing,
| Relinquitur ergo quod partes ipsius esse debeant inequales, ita quod unus sit prima pars; de uno ad tres, secunda; de tribus ad quinque, tercia; de quinque ad septem, quarta; de septem ad novem, quinta; et talis quinta pars est quintus numerus impar totius novenarii.10 |
| We acknowledge therefore that the parts of itself will have to be inequalities, so that 1 is the first part; from 1 to 3, the second; from the 3 to 5, the third; from 5 to 7, the fourth; from 7 to 9, the fifth; and such 5th part is the fifth odd number of the total 9. |
the "whole tone" seems to be first divided into 9 parts, then Marchetto explains that each of the 5 dieses is to be measured off as follows:
1st Diesis = the first part
2nd Diesis = from 1 to 3
3rd Diesis = from 3 to 5
4th Diesis = from 5 to 7
5th Diesis = from 7 to 9
Why did Marchetto first divide the "tone" into 9 parts in order to arrive at his 5-part division?
An interpretation proposed a decade ago by David Lenson, and its enthusiastic examination by Margo Schulter, assumes an equal 9-part division of the "whole tone", each part with an interval size of approximately 0.23 Semitones [= (9/8)(1/9) = 22.656+ cents], and various combinations of which make up Marchetto's "fifth-tones". This too I find unlikely.
Although Lenson at least deserves credit for incorporating Marchetto's clearly-stated 9-part division into his calculations, which Herlinger and apparently a long line of earlier theorists failed to do, it is highly dubious to assume that an equal division of an interval space was what Marchetto conceived.
The first thing to keep in mind was that Marchetto was not merely theorizing from his head onto paper -- he was illustrating his intonational theories by the time-honored method of making multiple divisions of a single monochord string, by means of moveable bridges. In addition to being a practical tangible acoustical experiment, this method uses an arithmetic division in its conception of segments of a pitch-space, sharply contrasted with both of the equal divisions -- the 5-part described by Herlinger and the 9-part of Lenson, which would both be characterized as geometric or logarithmic.
Marchetto assumes the standard 3-Limit or "Pythagorean" tuning of the music theories of his time in his description of the ratios of the basic intervals:
"octave" 2:1 "5th" 3:2 "4th" 4:3 "whole tone" 9:8 unison 1:1
Remembering that the "whole tone" was already specified as 9:8, it becomes clear that Marchetto's emphasis on 8 and 9 in the previous discussion on even and odd divisions refers to the ratio numbers in the "whole tone". This would probably have been more clearly expressed if the diagrams had looked like divisions of a monochord string, rather than an abstract multiplicative design.
Although not explicitly described this way, it seems to me that, in his explanation of divisions by 2 and 3, Marchetto's polemical stance against dividing the whole tone successively by 2 was probably referring to "quarter-tones" and "eighth-tones". At the start of his divisions, he is assuming a unity value of "1" for the "whole tone"; this unity is then divided in half, in other words, the tone is divided in two semitones, then each of those in half, thus the "quarter-tones", and so on.
Apparently, musicians and/or theorists had already once again begun discussing the possibility of smaller intervals than the semitone, possibly inspired by the revival in Italy of ancient Greek knowledge carried back from the Crusades. The Greeks in their theoretical treatises had spoken about and given measurements for the enharmonic genus, which contained small intervals that had been named "quarter-tones" by the influential theorist Aristoxenus in the 300s BC.
If my interpretation is correct, Marchetto apparently had a problem with "quarter-tones", either because did not feel that they accurately reflected the practice of his time, or, as we may gather from his own book, because he felt the mathematical divisions involved in calculating "quarter-tones" to be illogical.
The way Marchetto was thinking about ratios, as string-lengths on the monochord, is the opposite of the way we generally think about frequency ratios today (in terms of actual sound-wave frequencies). In the 8:9 ratio which constitutes the 'whole tone', the 8 represents the 'whole tone' which is measured off, and the 9 represents the whole length of string, which is the reference tone. (Conversely, we think of 8 as representing the reference tone on the bottom, and the 9 has the higher tone having a frequency 9/8, or 1.125, that of the lower tone.)
So for Marchetto, the semitones to be calculated had to fall between the whole string (= 9) and the bridge which stopped the interval of the 'tone' (= 8). The 9 obviously cannot be divided evenly in half, but it can be divided into 3 parts.
So he went thru the four-fold division process: ((1)/3)/3 = 1/9 and ((1/9)/3)/3 = 1/81, and arrived at a 9-part division of the 8:9, on analogy of the 8/9 of the of the whole monochord string which must be measured off to make the "whole tone". Ultimately, it is a method which goes back to the ancient Pythagorean ideal of all proportions based on multiples and divisions of 3.
Interestingly, however, the ratios which Marchetto achieved for his intervals actually have much higher-prime factors than the linear Pythagorean system.
If the string were divided up into 3 parts, then the first of those parts divided into 3 parts, and so on two more times, the procedure would be diagrammed thus:
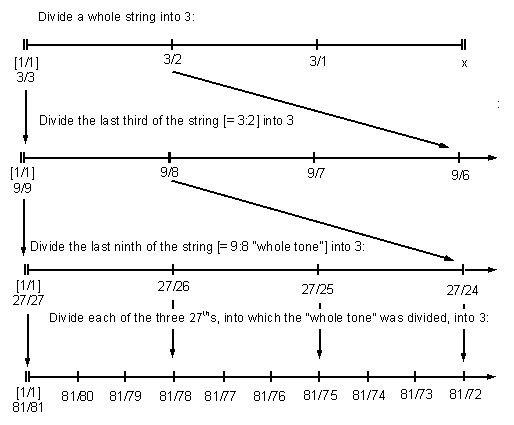
Counting from 0 at the nut of the monochord, if the 9 parts into which the first "whole tone" is now divided are numbered from 1 to 9, and the dieses marked off by bridges according to Marchetto's instructions, we arrive at:
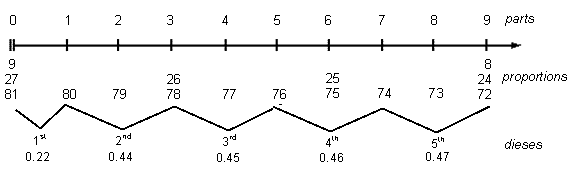
The most surprising thing to notice is that the Syntonic Comma is explicitly measured off as both the first part and the 1st Diesis. If this is correct, it would mark the Lucidarium as one of the earliest explicit notings of the role of the Syntonic Comma in the harmonic practice of medieval European music.
Marchetto continues, emphasizing the importance of recognizing these small intervals:
| Quarum quelibet quinta pars vocatur dyesis, quasi decisio seu divisio summa; hec est maior divisio que possit in tono cantabili reperiri.11 |
Lenson's translation:
| Any fifth part as it is desired, may be called a diesis, whether the lowest (smallest?) or the highest (largest?) division, this is the most important division that can be obtained in singing a tone." |
He is plainly using sloppy terminology here, stating that the term diesis can stand for any one of the five differently-sized intervals now obtained, four of them near-'quarter-tones' differing from each other by about 1 cent, and the other about half that size.
But he does seem to be stating that in singing, which would be naturally tuned in just-intonation or something close to it, it is well to recognize both an interval almost the size of a "quarter-tone", and another interval about half as large, the syntonic comma.
Actually, his wording seems to indicate to me, and my analysis below seems to bear out, that he was saying that it was important to be aware of a wide variety of small intervals which weave thru the musical fabric, and take on different musical functions depending on their context.
I think Marchetto's vagueness about the size of the diesis was quite deliberate, and after diagramming and exploring his rational divisions as explained in his book, we will see that Marchetto was actually dealing with a very subtle and sophisticated form of what I call bridging.
Because of this ambiguity, however, it is less clear exactly how Marchetto measured the three "semitones" on his monochord.
He describes them in pairs, the Enharmonic Semitone-Diatonic Semitone pair making up a tone, and the Chromatic Semitone-Diesis pair also making up a tone.
Since he gave ratios and clearly-labelled descriptions of the Enharmonic and Diatonic Semitones and how they combine to form a "whole tone", let us examine them first.
| tres vero ex istis dyesibus faciunt semitonium dyatonicum, quod maius est, quod quidem vocatur apotome maius, id est pars maior toni in duas divisi12 |
| It is true that from three of these dieses a diatonic semitone is made. This is the larger [semitone] which is called the major apotome. It is the larger part of the tone divided in two. |
Rationalizing them on his monochord as follows:
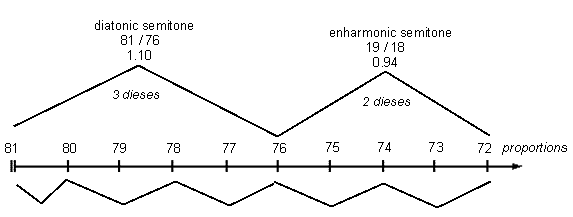
would have given Marchetto two unequal semitones very near in interval-size to the standard 3-Limit semitones and to the 5-Limit semitones that were probably already in practical use, and not far from the 16:17:18 which he used explicitly in the text to rationalize the division of the "whole tone".
A table of comparison is presented here with these ratios, those specified earlier by Marchetto as dividing the "whole tone", and the standard small 3-, 5- and 7-Limit intervals:
| Marchetto's term | ratios ratios 3-Limit 5-Limit semitone [= 76:72] 3-2191 0.94 3217-1 0.99 3-5 "limma" 0.90 3351 0.92 315-171 0.84 semitone 3419-1 1.10 171 1.05 37 "apotome" 1.14 3-15-1 "greater semitone" 1.12 31517-1 1.19 |
|---|
It must be noted that Marchetto's definition of the Diatonic and Enharmonic semitones as 16:17:18 uses the reverse kind of proportional measurement as the one he is demonstrating on the monochord, that is, as frequency proportions rather than as string-lengths. He is placing the larger, Diatonic, semitone first in both his proportional description and in his monochord measurement, and this can be reconciled only by using reverse perspectives.
Given as frequency proportions, Marchetto's monochord ratios for the Diatonic and Enharmonic semitones are expressed in lowest integer terms as 152:162:171.
Here is a table comparing the two as proportions:
|
81 : 76 : 72
---------- 81 | = | 304 : 324 : 342 |
| 16 : 17 : 18 | = | 304 : 323 : 342 |
The difference between 17/16 and 81/76 is
| 81:76 | = | 2-2 | 3 4 | 19-1 | |||
| ¸ | 17:16 | = | - | 2-4 | 17 1 | ||
| ___ | ___ | ____ | ___ | ||||
| 2 2 | 3 4 | 17 1 | 19-1 |
or 324:323 [= 5.35 cents].
16:17:18 is very close to his monochord
division of 81:76:72, and the
~ 5-cent difference
may or may not be audible, but on the monochord, depending
on the length of the string he used, it should have been easy
to see the difference visually, so it remains curious to
me why Marchetto chose to specify
that the Diatonic and Enharmonic semitones could be defined
as 16:17:18. I suspect that it has to do with my belief
that he was deliberately disregarding small differences
such as these in order to perform what Herlinger called
"numerological sleight of hand".
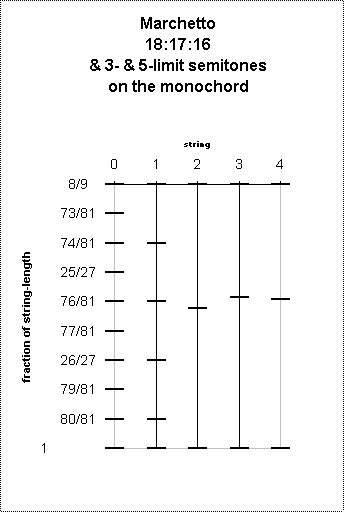
Here are two diagrams, showing first the placement of the monochord bridges, and next the Semitone values of the notes, for:
0. the 9-part division,
1. the 5 dieses,
2. the 16:17:18 division,
3. the standard 3-limit divisions of the "whole tone", and
4. the standard 5-limit divisions of the "whole tone":
|

|
Here the difference between 81/76 and 17/16 is plain. What is also very obvious from my diagram, however, is the fact that his 81:76:72 division is extremely close to both the Pythagorean and the 5-limit divisions of the "whole tone" into two "semitones".
|
update 2007.08.25: another possibility for division, based on counting the "first part" diesis at the higher note, and putting the diatonic-semitone at the top as in A:Bb:B
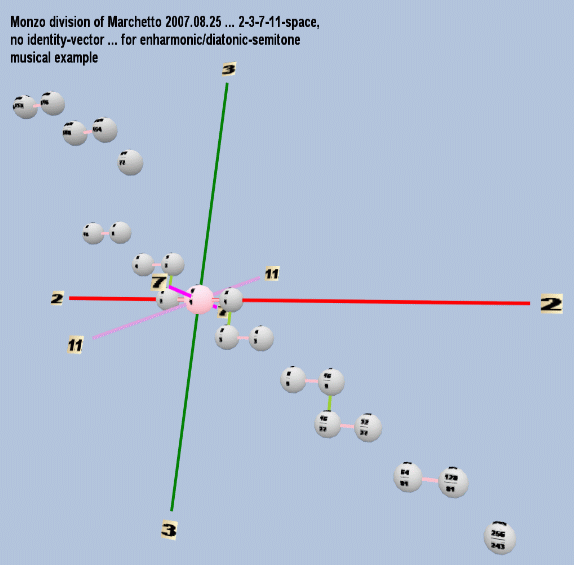
Note again the similarity of these to the standard pythagorean apotome Bb:B and limma A:Bb. This division utilizes the following 3==11-xenharmonic-bridge:
ratio 2,3,7,11-monzo
2304/2187 = 256/243 Bb [8 -5, 0 0>
/ 81/77 - Bb [0 4, -1 -1>
----------- ------------------
19712/19683 [8 -9, -1 -1> = ~2.55 cents:
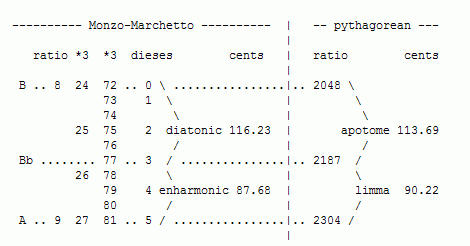
Another interpretation still puts the diatonic-semitone at the top, but counts the diesis from the bottom. Here is the Enharmonic and diatonic, diatonic on top, diesis at bottom:
--------------- Monzo-Marchetto ------------ | ------------- 5-limit --------
|
ratio *3 *3 dieses cents | ratio cents
|
B .. 8 24 72 .. 5 \ .......................|.. 1800 \
73 \ | \
74 4 \ | \
25 75 diatonic 13/12 138.6 | large semitone 27/25 133.2
76 3 / | /
77 / | /
Bb .... 26 78 .. 2 / .......................|.. 1944 /
79 \ | \
80 1 enharmonic 27/26 65.3 | small semitone 25/24 70.7
A .. 9 27 81 .. 0 / .......................|.. 2025 /
|
The enharmonic-semitone in this interpretation also resembles the interval used by Archytas at the bottom of each tetrachord in his PIS, in all genera: 28/27 = ~62.7 cents. It seems that Marchetto intended the "indivisible part in the middle" to represent the pythagorean-comma -- in my reference diagrams this would be between Bb and A#. But here it appears in the middle of the whole-tone, and Marchetto's description seems to place it at the beginning. Therefore, Marchetto apparently was thinking with C as his reference note, so that the "first diesis", which consists of only the "first part" (i.e., the first 1/9 part), measures the pythagorean-comma from C to B#:
--------------- Monzo-Marchetto ------------ | ------------- 5-limit --------
|
ratio *3 *3 dieses cents | ratio cents
|
D .. 8 24 72 .. 5 \ .......................|.. 1800 \
73 \ | \
74 4 \ | \
25 75 diatonic 13/12 138.6 | large semitone 27/25 133.2
C# 76 3 / | /
77 / | /
Db .... 26 78 .. 2 / .......................|.. 1944 /
79 \ | \
B# 80 1 enharmonic 27/26 65.3 | small semitone 25/24 70.7
C .. 9 27 81 .. 0 / .......................|.. 2025 /
|
We turn next to the 3-limit semitones, standardized for use by Marchetto's time from at least 1500 years of music-theory history. The progression 1/1 : 2187/2048 : 9/8 is expressed as a proportion in lowest integer terms as 2048:2187:2304. Here is a table comparing the proportions of Marchetto's monochord with the 3-limit semitones:
|
81 : 76 : 72
---------- 81 | = | 38912 : 41472 : 43776 |
| 2048 : 2187 : 2304 | = | 38912 : 41553 : 43776 |
The difference between 2187/2048 and 81/76 is
| 2187:2048 | = | 2-11 | 3 7 | |||
| ¸ | 81:76 | = | - | 2- 2 | 3 4 | 19-1 |
| ___ | ___ | ___ | ||||
| 2- 9 | 3 3 | 19 1 |
or 513:512 [= 3.378 cents]. Thus Marchetto's 81/76 "Diatonic Semitone" of 3 "dieses" is indeed very close to the "apotome" to which he equated it.
Surprisingly, however, it is even closer to the 5-limit larger semitone, which a few centuries later also became known as the "diatonic". The progression 1/1 : 16/15 : 9/8
[not yet available]
is expressed as a proportion in lowest integer terms as 120:128:135. Here is a table comparing the proportions of Marchetto's monochord with the 5-limit semitones:
|
81 : 76 : 72
---------- 81 | = | 2280 : 2430 : 2565 |
| 120 : 128 : 135 | = | 2280 : 2432 : 2565 |
The difference between 16/15 and 81/76 is
| 16:15 | = | 2 4 | 3-1 | 5-1 | |||
| ¸ | 81:76 | = | - | 2-2 | 3 4 | 19-1 | |
| ___ | ___ | ____ | ___ | ||||
| 2 6 | 3-5 | 5-1 | 19 1 |
or the tiny interval 1216:1215 [= 1.42 cents].
Using A n0 as a reference tone, we can attempt to construct a diagram of a system which contains all the notes used by Marchetto in his musical examples.13
It is important to keep in mind that at this stage in the
history of European music, notes were generally referred to as solfege syllables rather than
as absolute-pitch letter-names, and accidentals referred not to absolute pitches but
rather to mutations into new hexachords which would give the correct melodic interval sizes:
|
Semitonium dyatonicum est quando fit permutatio b rotundi in b quadrum vel e converso propter ascensum vel descensum, ut hic |

|
The diatonic semitone occurs when a permutation is made from round b to square b or vice versa, whether in ascent or descent, as here [musical example] 14 |
Using the ratios from my interpretation of Marchetto's monochord measurements, here is an analysis of the first example, illustrating Marchetto's Diatonic Semitone and Enharmonic Semitone, with my JustMusic prime-factor notation, ratios, and Semitone values, and the melodic intervals between notes in each voice:
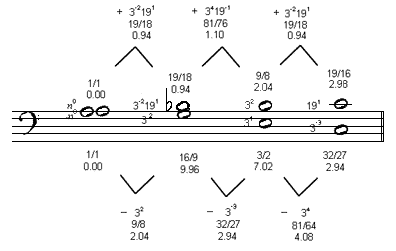
listen to enahrmonic and diatonic semitones, example
The harmonies, or simultaneously-sounding intervals, of this example are tabulated as follows:
| dyad: | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| prime-factor: | n0 | 191 | 31 | 2133191 |
| ratio: | 1/1 | 19/16 | 3/2 | 513/256 |
| Semitones: | 0.00 | 2.98 | 7.02 | 12.03 |
| interval: | unison | mistuned 32/27 | "p 5th" | mistuned 2/1 |
We can arrange the 7 notes used in this example onto a Lattice Diagram as follows (empty spaces indicate the missing 3-1 and 3-1191):
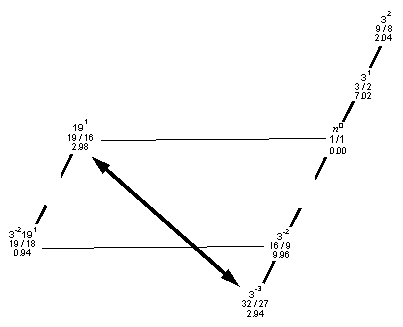
As indicated by the arrow, 191 is only approximately 0.04 Semitone
[33191 = 513/512 = 3.378+ cents] higher than
3-3, the standard Pythagorean "minor 3rd". This small interval may be called
the nondecimal schisma, and will be found useful
in a thorough analysis of Marchetto's purported tuning, as well as several ancient
Greek tunings using 19-Limit ratios. Its prime-factor notation is indicated clearly by
position on the Lattice.
I call small intervals like this "xenharmonic bridges", a term coined by Margo Schulter. The principle of bridges was recognized in the 1960s by Adriaan Fokker, who called them "unison vectors", and the main point about them is that they resemble other notes with different prime-factorization, enough so that we accept them as substitutes. This mental process enables us to reduce the complexity of a system containing large-prime ratios into a smaller, lower-limit one which is easier to comprehend, and in which it is easier to recognize patterns of intervals. My analysis of what I believe to have been Marchetto's method is an excellent example of the use of bridges.
|
update 2007.08.25: using my division of today, with the diatonic-semitone at the top as in A:Bb:B:
The entire diatonic PIS in this tuning is shown on the Tonescape® Lattice below, with the 5 pairs of 3-limit and 11-limit alternates in the lower-right and upper-left corners respectively:
|
Turning next to Marchetto's Chromatic Semitone, we will examine two possible interpretations of his instructions.
He briefly describes the diesis first, and this description naturally includes the Chromatic Semitone, as the two together make up a 'whole tone':
|
Et nota quod natura dyesis maxime cognoscitur per comparationem ad semitonium cromaticm, propter quod multum de dyesi ostendetur naturam cromatici ostendendo. |
|
Note that the nature of the diesis is best understood thru comparison with the chromatic semitone; much concerning the diesis will become clear as we demonstrate the nature of the chromatic semitone.15 |
The same information is repeated almost verbatim (just slightly more complete) a few chapters later, in discussion of the Chromatic Smitone itself.
|
Cromaticum semitonium est illud quod de quinque dyesibus quas habet tonus quatuor comprehendit, et, ut predicitur, semper cum dyesi tonum perficit. Fit enim cum aliquis tonus bipartitur propter aliquam dissonantiam colorandam, puta terciam, sextam, sive decimam tendendo ad aliquam consonantiam, nam prima pars toni sic divisibilis, si per ascensum fiat, erit maior, que dicitur croma; pars que restat dyesis est, ut hic: [musical examples] |
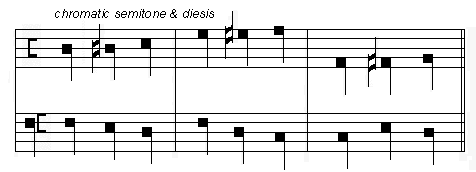
|
The Chromatic Semitone is that which includes 4 of the 5 dieses of the whole tone, and, as said earlier, it completes a whole tone when a diesis is added to it. It results when some whole tone is divided in 2 so as to color some dissonance such as a 3rd, a 6th, or a 10th striving toward some consonance. The first part of a tone thus divisible will be larger if the melody ascends, and is called a chroma; the part that remains is a diesis, as here: [musical example]16 |
Note the new symbol 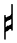 invented by
Marchetto to designate his Chromatic Semitone.
invented by
Marchetto to designate his Chromatic Semitone.
It is tempting to think that, at around the same time that Theinred of Dover and Walter Odington give tantalizing descriptions of 5-limit ratios being sung in place of 3-limit, Marchetto was overtly recognizing the syntonic comma, in view of the fact that it is explicitly measured off at the very beginning of his monochord. But we shall see that the description he gives follows more closely our second interpretation.
This first reading also produces results in Marchetto's own musical examples that sound much less than convincing in the context of the music of his time. But I still felt it worth examining, so the first, and in my opinion less likely reading, is as follows:
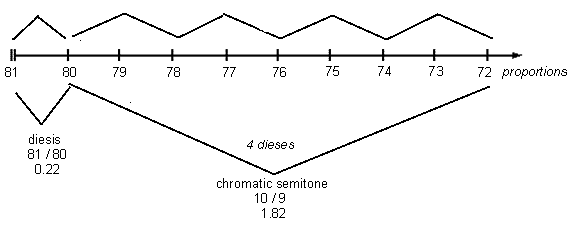
| Marchetto's term | ratios 3-Limit 5-Limit 345-1 0.22 312 "Pythagorean comma" 0.24 345-1 "Syntonic comma" 0.22 3-27-1 0.27 semitone [= 80:72] 3-251 1.82 3-10 1.80 3-251 "minor tone" 1.82 3471 1.77 |
|---|
An analysis of the first of his musical examples gives:
listen to chromatic semitone and diesis, example
The harmonies, or simultaneously-sounding intervals, of this example are tabulated as follows:
| dyad: | 1st | 2nd | 3rd |
|---|---|---|---|
| prime-factor: | 31 | 3-351191 | 33191 |
| ratio: | 3/2 | 95/54 | 513/256 |
| Semitones: | 7.02 | 9.78 | 12.03 |
| interval: | p 5th | mistuned 7/4 | mistuned 2/1 |
I give this reading only because it seemed a possibility to me, and will not follow the analysis of the musical examples further using this interpretation.
The second and more likely reading is given here, starting with a more in-depth exploration of Marchetto's descriptions of this interval combination.
Altho this combination may appear in a descending melodic line in the order Diesis > Chromatic Semitone, according to Marchetto:
|
Nisi fort fiat talis toni bipartitio per descensum, que est nimus propria in dissonantias tendentibus ad consonantias |
|
Such a division of the whole tone can also be made in descent when dissonances strive toward consonances, but less appropriately 17 |
So the 'normal' version is the ascending form, which he describes as the whole tone divided into the Chromatic Semitone first then the Diesis, not the other way around.
In either case, the Chromatic Semitone appears on the bottom and the Diesis on the top of the division anyway, so we will do the same in our examination.
Following his instructions exactly, if we start at the nut of the monochord, we measure off the 4 dieses of the chromatic semitone first, to arrive at the 81:74 chromatic semitone, then have the single 37:36 diesis left over at the end.
Lending further weight to this interpretation of his measurements is the definition Marchetto gives for the Chromatic Semitone as equalling a diatonic semitone plus a diesis:
|
ex dyatonico et dyesi [consurgit] cromaticum |
|
from the diatonic and diesis arise the chromatic18 |
Also, altho he doesn't state it exactly, he strongly implies that the diesis should be thought of as half an enharmonic semitone:
|
Due autem simul iuncte ex istis quinque componunt semitonium enarmonicum, quod minus est |
|
2 of these 5 intervals [the dieses] joined together make up the enharmonic semitone, which is the smaller 19 |
If my diagram of the diatonic and enharmonic semitione divisions of the monochord 9:8 is correct, then, on Marchetto's monochord, the 37:36 [= 74:72] diesis shown below would be physically an exact arithmetical division of the 19:18 [=76:72] enharmonic semitone diagrammed previously.
Here is the most likely interpretation of Marchetto's chromatic semitone and diesis, with the previous diagram of the diatonic and enharmonic semitones above for comparison:

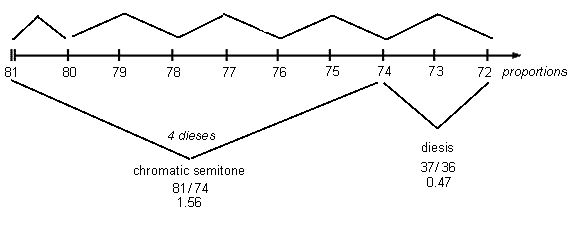
It can be easily seen that, as measured on the monochord, this chromatic semitone is visually as well as aurally not only a diatonic semitone plus a diesis, but also that the diesis comprises exactly half (in an arithmetical division of string-length) of the enharmonic semitone.
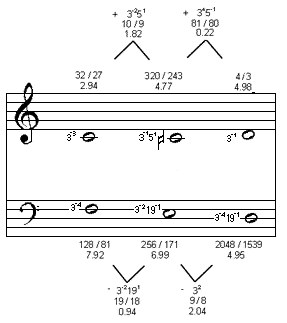
| Marchetto's term | ratios 3-Limit [= 74:72] 3-2371 0.47 0.47 5-3 0.41 325-17-1 0.49 semitone 3437-1 1.56 1.57 3253 1.63 5171 1.55 |
|---|
Interestingly, the 5-limit ratios are exactly those which would have the accidental as a "double-sharp" with the symbol x. This is a striking parallel with Marchetto.
Since the 7-limit ratios would have the same letter-names as the 1:1, with no accidental, and since the 3-limit system would have to be an enormous 46-tone linear system, which doesn't seem very likely for Marchetto's time and place, my suggestion is that his monochord division here was an attempt to accomodate the 5-limit intervals given above.
listen to chromatic semitone and diesis, example 1
listen to chromatic semitone and diesis, example 2
listen to chromatic semitone and diesis, example 3
........................................
Even though Lenson used an equal 9-part division of the "whole tone" in his reading, his semitones have interval sizes quite close to mine, and so I feel that his analysis of Marchetto's divisions is fairly accurate.
<< MORE TO COME HERE! including lattices! >>
Here is a lattice showing only those notes specifically indicated by Marchetto, assuming the usual 3-limit tuning as a base, and indicating in grey the 3==19 bridge. The isolated points are notes which are implied in his system, and which will be connected by bridges in the next lattice:
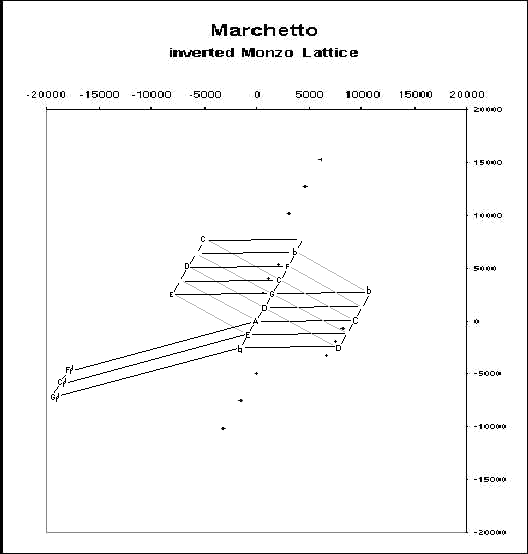
Below is a lattice in color showing several different bridges. The black lines are the regular prime vectors. The points shown in red are not part of Marchetto's system, but are merely given on the lattice as place-holders. The notes in his system are shown by black points, where they can be seen.
The connections in magenta show the 3==19 bridge given in the previous lattice, the regular 3851 3==5 bridge (the schisma), the 355119-1 5==19 bridge, and the 3-115-119-1 5==19 bridge, all occurring on symmetrically opposite sides.
The connections in blue show the 3-45171371 7==37 bridge, the 32527-1 5==7 bridge, and the 325-337-1 5==37 bridge. All of the periodicity blocks are clearly portrayed:
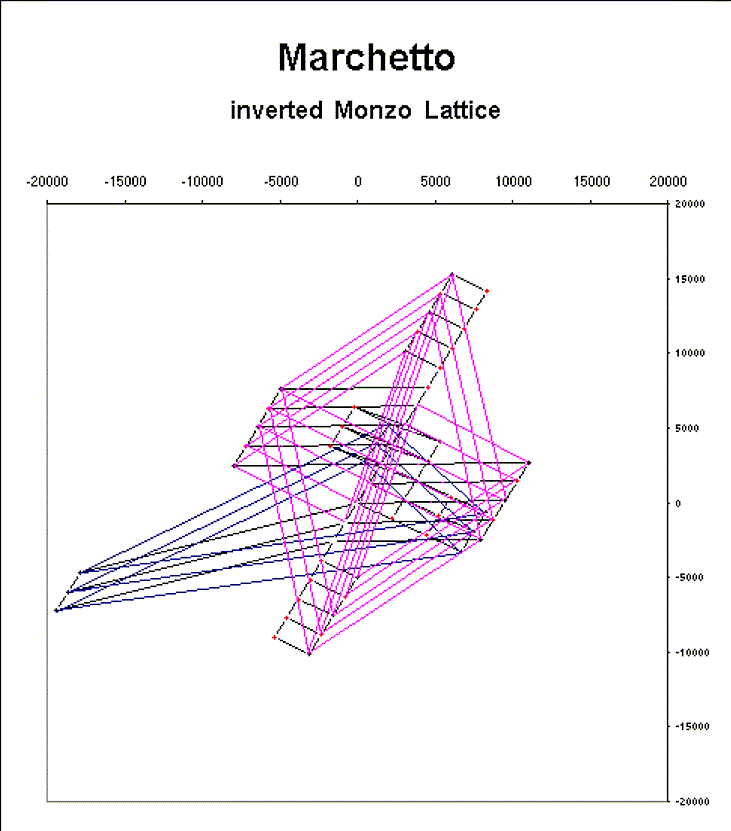
And here is another version with a grey background, which makes it a little easier to see the prime vectors:

An important point regarding Marchetto's shifting of semitone terminology: in 3-limit tuning, the diatonic semitone - the one between different scale-steps, the leimma - is 90 cents, and the chromatic semitone - the one between chromatically altered versions of the same scale-step, the apotome - was 114 cents. In 5-limit ratios, this is basically reversed: the diatonic is 112 cents and the chromatic 92
Marchetto's terminology differs from both of these. I think it reflects at least partly a shifting away from 3-limit tuning towards 5-limit.
This is not in evidence with the name 'chromatic'. The Pythagorean chromatic is larger than the 5-limit chromatic, but Marchetto's chromatic is much larger than both.
With the diatonic, on the other hand, altho it bears no relation to the 3-limit terminology, Marchetto's diatonic is only 2 cents smaller than the 5-limit diatonic semitone.
So it seems to me that Marchetto was recognizing that the very nature and tuning of the diatonic scale had changed by his day, with the diatonic semitone being smaller than the chromatic as in 5-limit, and in fact with the size of Marchetto's diatonic semitone nearly matching the 5-limit interval.
He logically gave the name "enharmonic" to the smallest of his three semitones, so it was actually close to what are called the Pythagorean diatonic and the 5-limit chromatic semitones.
But the point is that his calling the semitone of approximately 112 cents the diatonic is a clear recognition of the 5-limit diatonic usage which became standardized in theory only another 200 years later.
Basically, what Marchetto was doing was giving his own unique rationalization of "quarter-tones", in a way that probably related to the practice of his time.
As I noted earlier, ancient Greek writings were being brought back from the eastern Mediterranean after the Crusades, and the Greeks in many of their theoretical treatises had given different rationalizations of the "quarter-tones" of the enharmonic genus, and also in many of them espoused a Pythagorean point of view.
The "chronic 3-ism" of Pythagorean theory (as Harry Partch described it) was already deeply entrenched in medieval thought and religion, and it was Marchetto's unique genius to use a Pythagorean method of division, which he could justify philosophically, to arrive at high-prime ratios which acted as bridges to the 5- and 7- limit ratios he heard in the singing of his day which he most admired.
It is no wonder to me that his book was so widely influential in its day.
updated:
1997.02.04
1998.11.30
1999.03.31
A totally different interpretation:
SECOND DISCLAIMER: In the rush of excitement of discovering what I write about in the following, I state that I've found a new interpretation for Marchetto's divisions. After some further reflection, I see that it may not be correct, and that my original interpretation presented above may be right after all. This disclaimer remains until I have translated more of the Latin text and compared Marchetto's own statements with my claims.
I have made a new discovery in connection with Marchetto's theory, and will still be able to retain that as my last sentence. But a whole new article needs to be appended here, with entirely different ratios which I think portray Marchetto's design more accurately.
This new interpretation completely refutes the claims I made above for the possibility of Marchetto describing a 5-limit system. The ratios implied are beyond dispute all Pythagorean, and Marchetto's theory sheds an interesting light on the use of accidentals and mutation in music of his time.
It seems that Marchetto did not use the equal 9-part string division (which gives unequal intervals) that I explore above.
I will not delete it, however, because there is no way to be certain, and there is still a possibility that what I have there is correct. But my new interpretation of Marchetto's 'fifth-tones' fits all the evidence better, and strongly supports a 17-tone Pythagorean chromatic scale
Marchetto, in Treatise 2 chapter 4, is discussing the way that the continuum keeps getting smaller as one takes 8/9, and then 8/9 of 8/9, and so on, which was the standard Pythagorean way of building a scale by monochord division.
Since he does not give any actual measurements for his division of the 'whole tone', which is the source of all this confusion in the first place, I believe now that the reason Marchetto went thru this lengthy description of the 8:9 proportion is that this is the method he used in his 'whole tone' division.
He contrived a way of dividing the 'whole tone' that parallels the standard Pythagorean division of the whole string to produce the Pythagorean diatonic scale: taking the string length that produces the 'whole tone' itself (i.e., in comparison with the undivided string) as 1/9 of the entire string, then taking 8/9 of that, then 8/9 of 8/9, etc. etc.
So I applied this method to the division of the 8:9 'whole tone', instead of the 9 equal string-length divisions which I presented above, and I discovered something amazing.
I calculated that by dividing the 'whole tone' like this, marking off the dieses the way Marchetto indicated, and correllating his descriptions with the musical examples, he was simply measuring on the monochord a way to approximate (very closely: 2 cents error) the chromaticism that came into music in his time, but in the Pythagorean tuning!
With this method of division, Marchetto got a diesis at the end which was much larger than all the rest (92 cents! - the others are 22, 37, 30, and 24 cents), and ratios with some very high prime factors: his 'enharmonic semitone' is 531441 / 505160 [= 2-33125-173-1173-1] and his 'chromatic semitone' is 43046721 / 40360904 [= 2-33165045113-1].
However, they describe almost perfectly the method of Pythagorean chromaticism in the early 1300s, with only ~2 cents error.
Here are two diagrams, showing first the placement of the monochord bridges, and next the Semitone values of the notes, for:
0. the 9-part division,
1. the 5 dieses,
2. the 16:17:18 division,
3. the standard 3-limit divisions of the "whole tone", and
4. the standard 5-limit divisions of the "whole tone":
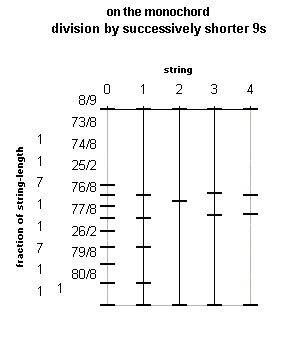
|

|
So, this is no evidence for 5-limit, as I was so sure of, but it's still a very clever method for expansion of the scale, and it uses *really* high primes (173, 5045113), a feature that became typical later in the Renaissance with writers like Colonna (webpage on him coming in the future).
It is important to remember, as I pointed out above, that accidentals at that time period did not mean the same thing they mean today. They signified not an absolute pitch value or pitch-class, but rather a variety of different 'mutations' which produced chromatic melodic progressions.
According to my new rational interpretation, the uses of Marchetto's four different small intervals can be summarized as follows, using regular Pythagorean terminology for 'natural', 'flat', and 'sharp':
|
diatonic semitone (~116 cents)
= from flat to natural above, or natural to flat below i.e., Bb->B or B->Bb |
|
enharmonic semitone (~88 cents)
= from natural to flat above, or flat to natural below i.e., A->Bb or Bb->A |
|
chromatic semitone (~112 cents)
= from natural to sharp above, or sharp to natural below i.e., A->A# or A#->A |
|
diesis (~92 cents)
= from sharp to natural above, or natural to sharp below i.e., A#->B or B->A# |
It turns out that the 'chromatic' and 'diatonic' semitones are very close in size: only ~4 cents difference. But they were differentiated by Marchetto because his perspective on accidentals was different from ours: the diatonic could only appear in conjunction with the enharmonic, and the chromatic only with the diesis, in specified melodic settings which Marchetto illustrates in the remainder of Lucidarium.
The vertical intervals (harmonies/ dyads) produced thru use of the chromatic semitone are not the unusual ones expanded by approximately a 'quarter-tone', but simply the regular Pythagorean *major* '3rds' and '6ths' minus ~2 cents (in places where these intervals would normally be of the 'minor' variety).
The 1962 article 'On the development of musical systems', by Kraehenbuehl and Schmidt, [Journal of Music Theory, vol 6, p 32-65] describes how Prosdocimus calculated the 17-tone Pythagorean scale by inserting a sharp *and* flat between all 7 of the regular Pythagorean diatonic notes.
Prosdocimus wrote his book about 100 years after Marchetto, and was bitterly attacking Marchetto's theories. But I can see, using this interpretation of Marchetto's divisions, that Marchetto was describing a very close approximation to exactly the same process which Prosdocimus 'corrected' (i.e., made strictly 3-limit).
I think this gives further validation to this new interpretation.
So, if this interpretation of his divisions is correct, and I think it is, he was not theorizing about 5-limit (JI) intervals at all, but merely describing the introduction of chromaticism into the music of his day within the Pythagorean system.
Nor did his 'chromatic semitone' indicate some pitch sharpened by about a 'quarter-tone'.
I personally am a little disappointed about both of those, but it is still a very clever theory.
And the accepted view on Marchetto's 'fifth-tones', Herlinger's, is in serious need of correction.
Also, Jay Rahn published his article on Marchetto in Music Theory Online last December, with exactly the same measurements I discuss on the older part of this page. This view also needs to be emended.
Update 2000.10.8: I don't think this interpretation is correct, because no matter how I try to manipulate the arrangement of dieses, I can't make the Diatonic Semitone equal the Apotome and still be composed of 3 dieses. So the earlier, simpler interpretation must be correct.
28 April 1999
update from 2008.08.14,
posted originally to Yahoo tuning, message 78191 [Thu Aug 14, 2008 11:24 pm UTC].
It has always bothered me that Marchetto first divides the whole-tone into 9 parts, _then_ uses only the odd-numbered portions of that to achieve his 5-part division. What makes it really irksome is that he writes "the first part is the first diesis", and then describes the other four dieses as "from the first to the third", "from the third to the fifth", etc.
So in a flash of sudden insight, i realized that perhaps he was thinking of the integers the old-fashioned way, that is, _without zero as part of the set_!
If he started by counting the whole monochord string as the "first part" -- instead of the "zeroeth part" as we would do it today (and as i did in my webpage diagrams) -- then he could have a 9-part division of the whole-tone by labeling the divisions thus:
72 . 71 . 70 . 69 . 68 . 67 . 66 . 65 . 64 -- arithmetic part 1 .. 2 .. 3 .. 4 .. 5 .. 6 .. 7 .. 8 .. 9 --- Marchetto "part" 1 ....... 2 ....... 3 ....... 4 ....... 5 --- Marchetto diesis 0 ....... 49 ...... 99 ...... 151 ..... 204 - ~cents
If this is the proper interpretation, then all Marchetto was doing after all, was describing what are essentially quarter-tones.
No great argument from me yet in support of this interpretation -- it's just another of the many possibilities i and others have already thought up.
NOTES
All references to Lucidarium are given in the form:
treatise(= book).chapter.paragraph
| 1 | Lucidarium is a Latin word
meaning 'bringer of light', or 'illuminator'.
(  back to text) back to text)
|
| 2 | See Herlinger's The Lucidarium
of Marchetto of Padua,
a Critical Edition, Translation, and Commentary, University of Chicago Press, 1985. Also Marchetto's Division of the Whole Tone Journal of the American Musicological Society, vol 34 no 2, p 193-216. (  back to text) back to text)
|
| 3 | Marchetto 1318, Lucidarium,
1. 16. 5.;
see Herlinger 1985, p 104-107. I think I would leave Herlinger's 'clarifying' editorial insertion of 'species' out of the translation. (  back to text) back to text)
|
| 4 | The entire Latin text of
the treatise can be downloaded here
(  back to text) back to text)
|
| 5 | Marchetto 1318, Lucidarium,
2. 9. 1-13.;
see Herlinger 1985, p 159-161. (  back to text) back to text)
|
| 6 | Marchetto 1318, Lucidarium,
2. 4. 2-7.;
see Herlinger 1985, p 110-113. (  back to text) back to text)
|
| 7 | Marchetto 1318, Lucidarium,
2. 4. 9-11.;
see Herlinger 1985, p 112-115. (  back to text) back to text)
|
| 8 | Marchetto 1318, Lucidarium,
2. 4. 12.;
see Herlinger 1985, p 114-115. (  back to text) back to text)
|
| 9 | Marchetto 1318, Lucidarium,
2. 4. 9-19.;
see Herlinger 1985, p 112-121. The manuscript tradition of Lucidarium is
outlined excellently in Herlinger's introduction. According to that,
the oldest manuscript in existence is an ornate presentation copy
that was probably given to the treatise's dedicatee, and in this
manuscript there is a space for these diagrams, but the diagrams
themselves were never copied into the manuscript. So all surviving
diagrams originated with later scribes.
|
| 10 | Marchetto 1318, Lucidarium,
2. 5. 13-14.;
see Herlinger 1985, p 134-135. (  back to text) back to text)
|
| 11 | Marchetto 1318, Lucidarium,
2. 5. 23-24.;
see Herlinger 1985, p 138-139. (  back to text) back to text)
|
| 12 | Marchetto 1318, Lucidarium,
2. 5. 26.;
see Herlinger 1985, p 140-141. (  back to text) back to text)
|
| 13 | Again, I am not sure if these examples
are original with Marchetto or solely the work of later scribes.
I am presently researching the origin of the examples.
(  back to text) back to text)
|
| 14 | Marchetto 1318, Lucidarium,
2. 7. 6.;
see Herlinger 1985, p 144-145. The musical example for the diatonic and enharmonic semitone is
Herlinger's 'example 4', p 145.
Brussels, Bibliolthèque Royale Albert Premier, II 785, ff. 15r-38v.
|
| 15 | Marchetto 1318, Lucidarium,
2. 6. 5.;
see Herlinger 1985, p 142-143. (  back to text) back to text)
|
| 16 | Marchetto 1318, Lucidarium,
2. 8. 2-4.;
see Herlinger 1985, p 148-149. The example of the chromatic semitone and diesis is
Herlinger's 'example 5', p 150-151
|
| 17 | Marchetto 1318, Lucidarium,
2. 8. 8.;
see Herlinger 1985, p 152-153. (  back to text) back to text)
|
| 18 | Marchetto 1318, Lucidarium,
2. 7. 13;
see Herlinger 1985, p 148-149. (  back to text) back to text)
|
| 19 | Marchetto 1318, Lucidarium,
2. 5. 25.;
see Herlinger 1985, p 138-139. (  back to text) back to text)
|
REFERENCES
Marchetto of Padua, c. 1318. Lucidarium
Thesarus Musicarum Latinarum.
Jan W. Herlinger, 1981. Marchetto's Division of the Whole Tone
Journal of the American Musicological Society, vol 34 no 2, p 193-216.
Jan W. Herlinger, 1985. The Lucidarium of Marchetto of Padua (1317-18).
David Lenson, 1987.
University of Chicago Press, Chicago.
Nonspecific
Accidentals: A study in medieval temperament based on notation
MA thesis, University of Western Ontario.
-
< Lenson's study of Marchetto is
here>
Joseph L. Monzo, 1997-8. JustMusic: A New Harmony
Sonic Arts Press, San Diego (forthcoming)
Margo Schulter, 1998.
Marchettus of Padua's tuning
and Gothic cadential aesthetics.
Mills College Tuning Digest, no 1580, topics 10 & 11.
- links to related topics:
- Jay Rahn's Practical Aspects of Marchetto's Tuning, from MTO 4.6
-
Margo Schulter, 2000.8.25.
More on 29-tet -- a beautiful tuning,
Egroups Tuning List, message 11873
updated:
2007.08.25 -- added yet another interpretation for diatonic- and enharmonic-semitones