meantone family tunings -
error from 11-limit just intonation
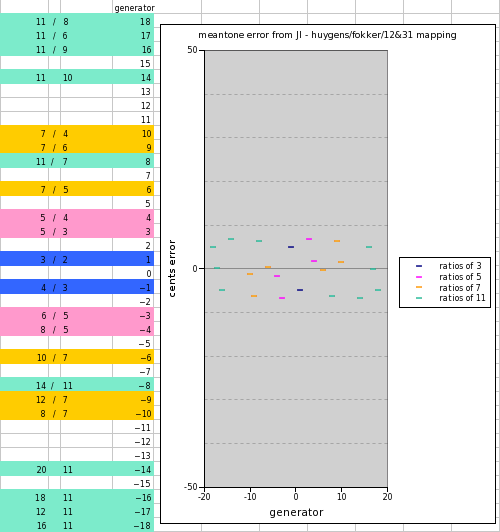
Below is an applet illustrating the amount of error from the basic 7-limit JI intervals, in fractions of a syntonic comma, of various meantone tunings.
MouseOver the names of the various meantone cycles to see a graph of the error. (The labels showing the amount of error are sometimes exact and other times only approximate: accurate to one or two digits in each term of the fraction)
|
19-edo 1/3-comma LucyTuning 2/7-comma 50-edo 7/26-comma golden 1/4-comma 31-edo 3/13-comma Glasier optimal 136-edo 2/9-comma 43-edo 55-edo 1/6-comma 12-edo |
|
The ratios are mapped to meantone generators as follows:
ratios of 11 ratios of 7 ratios of 5 ratios of 3 ratios of 5 ratios of 7 ratios of 11 -18 -17 -16 ... -10 -9 -8 ... -6 ... -4 -3 ... -1 ... +1 ... +3 +4 ... +6 ...+8 +9 +10 ... +16 +17 +18 16/11 12/11 18/11 8/7 12/7 14/11 10/7 8/5 6/5 4/3 3/2 5/3 5/4 7/5 11/7 7/6 7/4 11/9 11/6 11/8
It can be seen that the lowest overall error in the 11-limit is given by meantones in the area of 3/13-comma to 136edo (in the version of 136edo where the "5th" is mapped to 79 degrees).
Looking at only the blue plots, it can be seen that 2/7-comma gives the lowest maximum error for all four "ratios of 5" -- in this case, all four ratios have exactly the same amount of error (1/7-comma), so in a sense it is the "balancing point" for meantone errors for the "ratios of 5".
Looking at only the red and the blue plots, it can be seen that 1/4-comma gives the lowest maximum error for all ratios within the 5-limit -- one pair of "ratios of 5" is given exactly as the JI ratios, and the other pair of "ratios of 5" and both of the "ratios of 3" are given with exactly 1/4-comma error.
Looking at the red, blue, and yellow plots, it can be seen thet 1/4-comma also gives the lowest maximum error for all ratios within the 7-limit.
31edo is the lowest-cardinality closed meantone which gives fairly good approximations to all ratios within the 11-limit.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
