A term coined in July 2003 by a group of tuning theorists (including Aaron Hunt, Gene Ward Smith, and Joe Monzo), to describe one of a family of terms referring to units of resolution in MIDI tuning, used in electronic music software and computer music software. The prefix specifies the exponent of 2 which describes the number of MIDI tuning units per semitone, and the final "mu" is an acronym for "MIDI unit". In this work the numerical figure is used in preference to the verbal prefix.
At the setting for 12mu pitch-bend resolution, a semitone is divided into 212 = 4096 pitch-bend units. Thus there are 4096 * 12 = 49152 12mus in an "octave", so the 12mu measurement system may be thought of as 49152-edo tuning, with a 12mu being one degree in 49152-edo.
A 12mu is calculated as the 49152nd root of 2 -- 49152√2, or 2(1/49152) -- with a ratio of approximately 1:1.000014102. It is an irrational number, but is extremely close to the ratio 70913:70912 : the difference is less than 1/2,500,000 of a cent, which for all intents and purposes makes the 12mu identical to that ratio. The formula for calculating the 12mu-value of any ratio is: 12mus = log10(ratio) * [ (212 * 12) / log10(2)] or 12mus = log2r * (212 * 12) , where r is the ratio.
A 12mu is:
The internal data structure of the 12mu requires two bytes, with the first bits of each byte reserved as a flags to indicate the byte's status as data, and one bit in the first byte to indicate the sign (+ or -) showing the direction of the pitch-bend up or down, and 1 other bit which is not used. The first data byte transmitted is the Least Significant Byte (LSB), equivalent to a fine-tuning. The second data byte transmitted is the Most Significant Byte (MSB), equivalent to a coarse-tuning.
let "d" designate the bits that cannot be used
because it is reserved for the SysEx flag, to
indicate that this is a byte of pitch-bend data.
let "s" designate the bit that represents the
sign of the pitch-bend data, + or - .
let "x" designate unused bits
the 12mu spec thus uses a total of 7+5 = 12 bits.
thus, the maximum possible value is:
-- LSB -- -- MSB --
d111 1111 dxs1 1111 [binary]
= +/- 3F 7F [hex]
= +/- 8191 [decimal]
note that the first nibble of the MSB can only indicate the
sign + or - and the data-values 0 or 2048 [decimal].
Below is an illustration of exactly how this works.
The "x" represents the status flag at the beginning of the byte, and is not recognized as part of the tuning resolution. The bit which represents 64 [decimal] is the sign bit. The actual tuning data begins with the bit representing 32 [decimal]. x 64 32 16 8 4 2 1 x 8192 4096 2048 1024 512 256 128 -- decimal value x 0 0 0 0 0 0 1 x x 1 0 0 0 0 0 = 20 01 hex = 4097 decimal = one unit (0.024414063 = 25/1024 cents) above the 12-edo MIDI-note x 64 32 16 8 4 2 1 x 8192 4096 2048 1024 512 256 128 -- decimal value x 0 0 0 0 0 0 0 x x 1 0 0 0 0 0 = 20 00 hex = 4096 decimal = the plain MIDI-note, 0 cents deviation from 12edo. x 64 32 16 8 4 2 1 x 8192 4096 2048 1024 512 256 128 -- decimal value x 1 1 1 1 1 1 1 x x 0 1 1 1 1 1 = 1F 7F hex = 4095 decimal = one unit (0.024414063 = 25/1024 cents) below the 12-edo MIDI-note
Therefore the 12mu gives a range of possible values +/- as follows -- the top end, middle, and bottom end of the range are shown for illustration. (Also shown is one section where the cents values become offset -- i.e., because one increment is 25/1024 of a cent, and 1024 does not divide evenly by 25, there will be a value of 1025/1024 cents.):
The 212 bit represents the sign +/- . Numbers under "LSB" and "MSB" are the exponent of 2 which that bit represents. ---------------------- bits ----------------------- -------- LSB ---------- -------- MSB ---------- --------- cents -------- x 6 5 4 3 2 1 0 x 13 12 11 10 9 8 7 hex decimal decimal fraction x 0 0 0 0 0 0 0 x (1) 0 0 0 0 0 0 40 00 8192 +100 x 1 1 1 1 1 1 1 x x 1 1 1 1 1 1 3F 7F 8191 + 99.97558594 + 99 999/1024 x 1 1 1 1 1 1 0 x x 1 1 1 1 1 1 3F 7E 8190 + 99.95117188 + 99 974/1024 x 1 1 1 1 1 0 1 x x 1 1 1 1 1 1 3F 7D 8189 + 99.92675781 + 99 949/1024 . . . x 0 1 0 1 0 1 0 x x 1 0 0 0 0 0 20 2A 4138 1.025390625 + 1 26/1024 x 0 1 0 1 0 0 1 x x 1 0 0 0 0 0 20 29 4137 1.000976563 + 1 1/1024 = 1025/1024 x 0 1 0 1 0 0 0 x x 1 0 0 0 0 0 20 28 4136 0.9765625 + 1000/1024 x 0 1 0 0 1 1 1 x x 1 0 0 0 0 0 20 27 4135 0.952148438 + 975/1024 . . . x 0 0 0 0 0 1 1 x x 1 0 0 0 0 0 20 03 4099 + 0.073242188 + 75/1024 x 0 0 0 0 0 1 0 x x 1 0 0 0 0 0 20 02 4098 + 0.048828125 + 50/1024 x 0 0 0 0 0 0 1 x x 1 0 0 0 0 0 20 01 4097 + 0.024414063 + 25/1024 x 0 0 0 0 0 0 0 x x 1 0 0 0 0 0 20 00 4096 0 0 x 1 1 1 1 1 1 1 x x 0 1 1 1 1 1 1F 7F 4095 - 0.024414063 - 25/1024 x 1 1 1 1 1 1 0 x x 0 1 1 1 1 1 1F 7E 4094 - 0.048828125 - 50/1024 x 1 1 1 1 1 0 1 x x 0 1 1 1 1 1 1F 7D 4093 - 0.073242188 - 75/1024 x 1 1 1 1 1 0 0 x x 0 1 1 1 1 1 1F 7C 4092 - 0.09765625 - 100/1024 . . . x 0 0 0 0 1 0 0 x x 0 0 0 0 0 0 00 04 4 - 99.90234375 - 99 924/1024 x 0 0 0 0 0 1 1 x x 0 0 0 0 0 0 00 03 3 - 99.92675781 - 99 949/1024 x 0 0 0 0 0 1 0 x x 0 0 0 0 0 0 00 02 2 - 99.95117188 - 99 974/1024 x 0 0 0 0 0 0 1 x x 0 0 0 0 0 0 00 01 1 - 99.97558594 - 99 999/1024 x 0 0 0 0 0 0 0 x x 0 0 0 0 0 0 00 00 0 -100 -100
For practical use in tuning MIDI-files, an interval's semitone value must first be calculated. The nearest integer semitone is translated into a MIDI note-number (which can generally also be described by letter-name plus optional accidental: A, Bb, C#, etc., followed by an "octave" register-number, as A-1, Bb2, etc.). Then the remainder or deficit is converted into 12mus plus or minus, respectively.
12mu-sizes for some small intervals, with cents-values given for comparison:
interval ------------ 12mus ----------- cents
integer decimal fraction
Pythagorean comma 961 ~960.9220254 ~960 13/14 ~23.46001038
53edo comma 927 ~927.3962264 ~927 2/5 ~22.64150943
syntonic comma 881 ~880.8976219 ~880 8/9 ~21.5062896
72edo morion 683 ~682.6666667 682 2/3 16 2/3
kleisma 332 ~332.0741422 ~332 1/13 ~8.107278862
heptameride 163 ~163.2956811 ~163 2/7 ~3.986710963
savart 164 163.84 ~163 5/6 4
grad 80 ~80.07683545 ~80 1/13 ~1.955000865
skhisma 80 ~80.02440347 ~80 1/41 ~1.953720788
millioctave 49 49.152 ~49 1/7 1.2
türk cent 46 ~46.36981132 ~46 3/8 ~1.132075472
cent 41 40.96 40 24/25 1
monzisma 12 ~11.9765283 ~11 83/85 ~0.039863137
1/8-skhisma 10 10.00305043 ~10 1/328 ~0.244215098
jot 2 ~1.632794074 ~1 5/8 ~0.039863137
14mu 0 0.25 1/4 ~0.006103516
Note the accuracy of 10 12mus approximating 1/8-skhisma. This means that Cakewalk and other software with this resolution represents 1/8-skhisma temperaments (like those of Groven and Helmholtz) remarkably accurately.
Because 12-edo is nearly identical to 1/11-comma meantone, if you do much manual pitch-bend entry in Cakewalk to retune music from 12edo into 5-limit just intonation, you'll find yourself using the following numbers again and again:
x/11-comma 12mus
1 80
2 160
3 240
4 320
5 400
6 480
7 561
8 641
9 721
10 801
11 881
12 961
13 1041
14 1121
15 1201
16 1281
17 1361
18 1441
19 1522
20 1602
21 1682
22 1762
23 1842
24 1922
25 2002
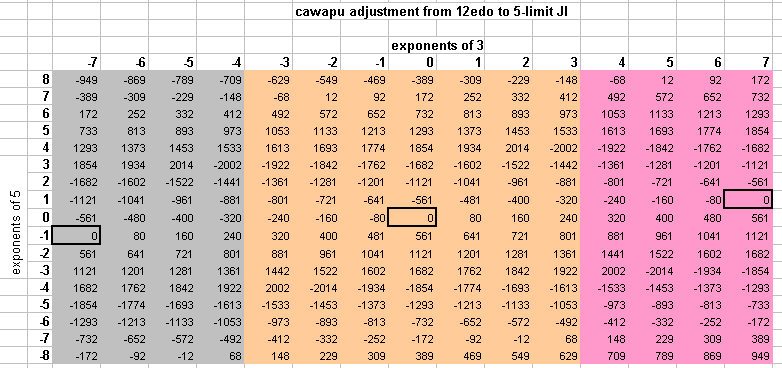
Below is a 5-limit lattice-diagram showing the amount of 12mu adjustment necessary to retune from 12-edo into just intonation. Note periodicity (shown by different colors), in which the amount of adjustment for the monzo (interval-vector) [* 7, 1> is zero.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.