canasta scale
(canasta = Spanish, "basket")
A 31-tone scale belonging to the miracle family of temperaments, derived from an optimal MIRACLE generator, and in one form a subset of 72-edo. For its relatively small size, this scale approximates an enormous number of 3-limit, 5-limit, 7-limit, and 11-limit just-intonation harmonic structures.
In keeping with the name of its smaller relative, the blackjack scale, it was dubbed "canasta" on the misconception that the card game used 31 cards. Those who know the game are aware that this is not the case, and for a while the scale was called miracle-31. But later, when the meaning of the Spanish word was discovered, it was decided after all that "canasta" was an entirely appropriate name to describe this scale which contains so many harmonic resources, and that miracle could therefore be reserved to designate the generator itself and the whole family of tunings.
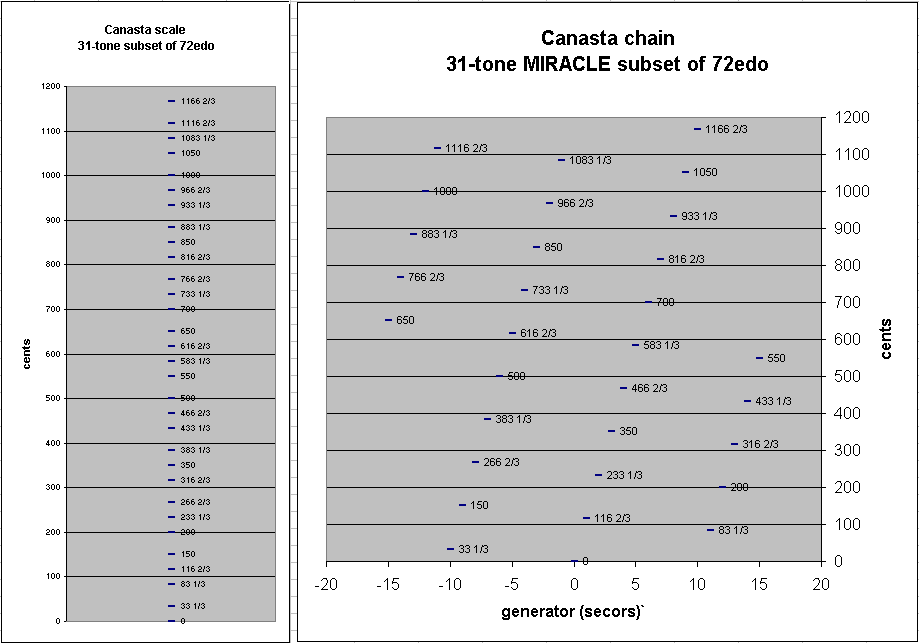
Below are graphs of the cents-values of the pitches in a typical Canasta chain, illustrated on the left as a scale and on the right as a chain of generators from -15 to +15 secors.
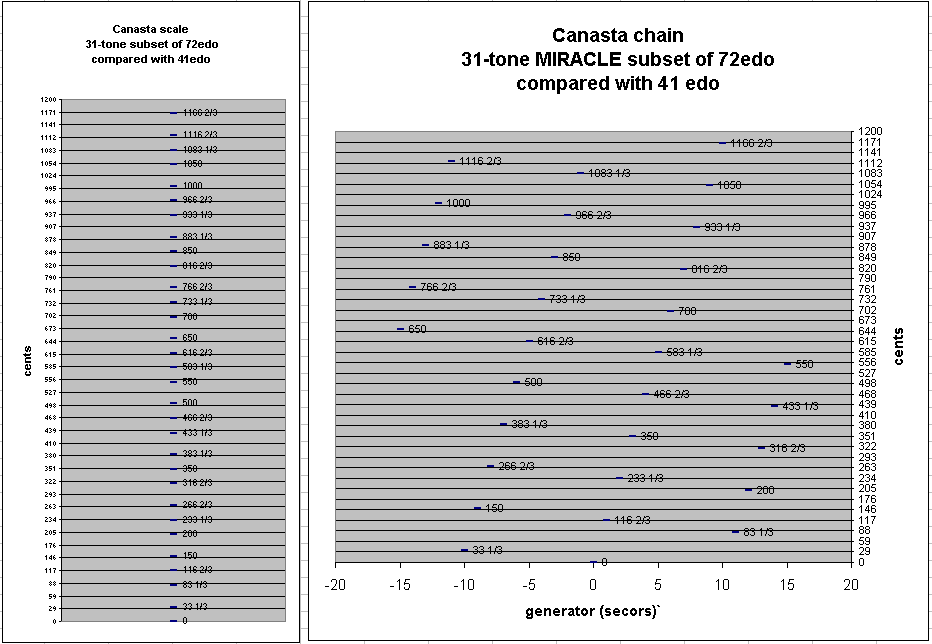
Below are the same graphs, but this time with the y-axis quantized into 41edo instead of 12edo, which shows how closely 41edo approximates the 72edo version of Canasta. (There are 4 degrees of 41edo in a secor.)
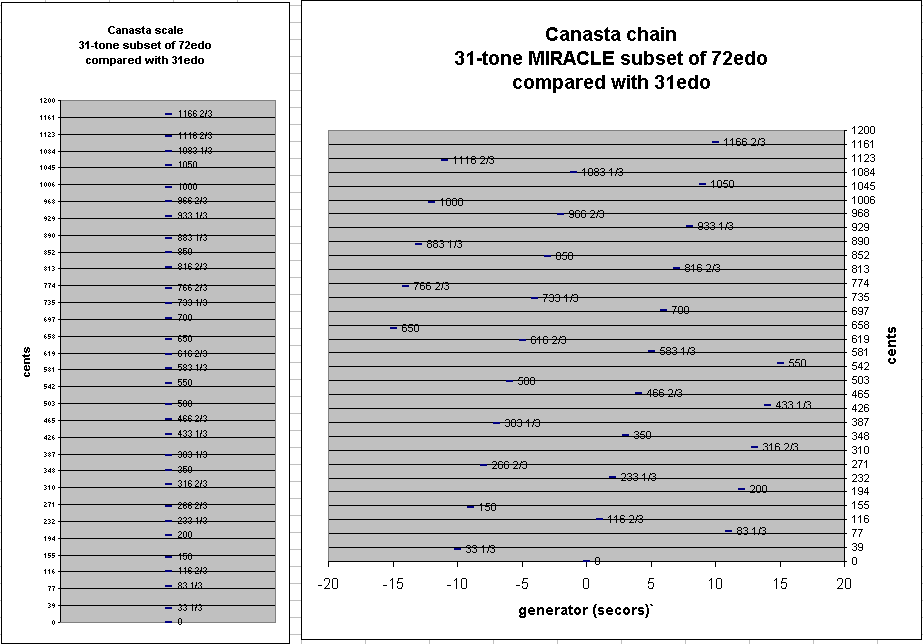
Finally, below are the same graphs again, but this time with the y-axis quantized into 31edo, which shows how closely 31edo approximates the 72edo version of Canasta. (There are 3 degrees of 31edo in a secor.)
Below is a more accurate assessment of exactly how the 72-edo and 31-edo versions of canasta differ:
--------------- cents --------------------
generator 72-edo 31-edo diff of 31 from 72
-15 650 658.&02/31 + 8.064516129
-14 766.&2/3 774.&06/31 + 7.52688172
-13 883.&1/3 890.&10/31 + 6.989247312
-12 1000 1006.&14/31 + 6.451612903
-11 1116.&2/3 1122.&18/31 + 5.913978495
-10 33.&1/3 38.&22/31 + 5.376344086
-9 150 154.&26/31 + 4.838709677
-8 266.&2/3 270.&30/31 + 4.301075269
-7 383.&1/3 387.&03/31 + 3.76344086
-6 500 503.&07/31 + 3.225806452
-5 616.&2/3 619.&11/31 + 2.688172043
-4 733.&1/3 735.&15/31 + 2.150537634
-3 850 851.&19/31 + 1.612903226
-2 966.&2/3 967.&23/31 + 1.075268817
-1 1083.&1/3 1083.&27/31 + 0.537634409
0 0 0 0
+1 116.&2/3 116.&04/31 - 0.537634409
+2 233.&1/3 232.&08/31 - 1.075268817
+3 350 348.&12/31 - 1.612903226
+4 466.&2/3 464.&16/31 - 2.150537634
+5 583.&1/3 580.&20/31 - 2.688172043
+6 700 696.&24/31 - 3.225806452
+7 816.&2/3 812.&28/31 - 3.76344086
+8 933.&1/3 929.&01/31 - 4.301075269
+9 1050 1045.&05/31 - 4.838709677
+10 1166.&2/3 1161.&09/31 - 5.376344086
+11 83.&1/3 77.&13/31 - 5.913978495
+12 200 193.&17/31 - 6.451612903
+13 316.&2/3 309.&21/31 - 6.989247312
+14 433.&1/3 425.&25/31 - 7.52688172
+15 550 541.&29/31 - 8.064516129
Below is a tabulation of the (-15...+15) canasta in 72-edo, 41-edo, and 31-edo. My 72-edo HEWM notation, Graham Breed's decimal notation, and cents-values are also given.
HEWM 31-edo 41-edo 72-edo cents Breed decimal
degree degree degree degree
C< 30 40 70 1166.&2/3 0v
B+ 29 38 67 1116.&2/3 9^^
B- 28 37 65 1083.&1/3 9^
Bv 27 36 63 1050 9
Bb 26 34 60 1000 8^^
Bb< 25 33 58 966.&2/3 8^
A> 24 32 56 933.&1/3 8
A- 23 30 53 883.&1/3 7^^
Av 22 29 51 850 7^
G#+ 21 28 49 816.&2/3 7
G#< 20 26 46 766.&2/3 6^^
G> 19 25 44 733.&1/3 6^
G 18 24 42 700 6
Gv 17 22 39 650 5^^
F#+ 16 21 37 616.&2/3 5^
F#- 15 20 35 583.&1/3 5
F^ 14 19 33 550 5v
F 13 17 30 500 4^
F< 12 16 28 466.&2/3 4
E> 11 15 26 433.&1/3 4v
E- 10 13 23 383.&1/3 3^
Ev 9 12 21 350 3
Eb+ 8 11 19 316.&2/3 3v
Eb< 7 9 16 266.&2/3 2^
D> 6 8 14 233.&1/3 2
D 5 7 12 200 2v
Dv 4 5 9 150 1^
C#+ 3 4 7 116.&2/3 1
C#- 2 3 5 83.&1/3 1v
C> 1 1 2 33.&1/3 0^
C 0 0 0 0 0
Note that the full set of 31-edo acts simultaneously as both a closed meantone (specifically, 1/4-comma meantone) and as the canasta form of miracle. 31-edo also belongs to other temperament families.
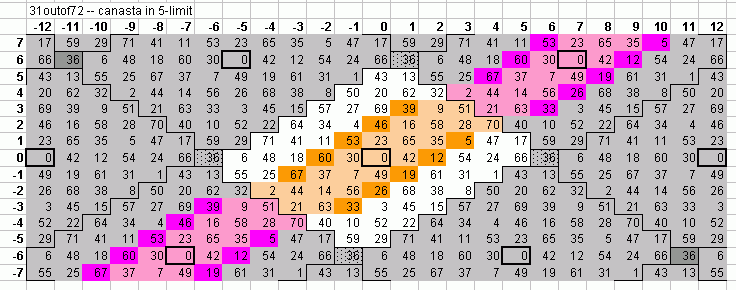
Below is a 5-limit bingo-card-lattice of 72edo, with the canasta scale shown in buff in the central periodicity-block and in pink in the blocks which are commatic equivalents. The subset of canasta which comprises the blackjack scale is shown in lighter shades.
In May 2001 I devised this mapping of almost 2 octaves of the Canasta scale to the standard QWERTY computer keyboard, for use with my JustMusic software. The pitches are given in my ASCII 72-edo HEWM notation.

The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
