© 1998 by Joseph L. Monzo
Donald Lentz, in Tones and Intervals of Hindu Classical Music, gives a description of ancient Indian tuning as a series of "perfect 4ths" and "perfect 5ths", which would give a "Pythagorean" or 3-Limit system of 22 notes ("srutis") to the "octave". He then gives a tabulation of the ratios, but, interestingly, it includes 5-Limit ratios as replacements for some which should be 3-Limit.
I would argue, however, that the theoretical implications of the ancient Indian tuning would allow even more 5-limit ratios than Lentz's description.
Before I discuss Indian tuning, a note about my somewhat idiosyncratic nomenclature:
In my prime-factor notation, 1/1 is referred to as n0 (that is, every prime to the 0th power, which equals 1). I use a measurement of "Semitones" to two decimal places rather than cents, simply because anything less than a cent is usually insignificant, at least for purposes of music-theory, and it relates better to our familiar old 12-EQ scale. (It's really the same as cents, just with a decimal point.)
Now, on with the show:
Lentz gives the most ancient Indian fretting as a series of "perfect 4ths and 5ths". This makes a lot of sense, as it could have been easily accomplished by ear. It can be measured for one "octave" on a single string in two separate procedures, as follows:
(frets are numbered in order of placement during the procedure, not in order of pitch)
PROCEDURE OF TUNING ANCIENT INDIAN SYSTEM:
| FRET | INTERVAL | POWER OF 3 | SEMITONES | RATIO |
|---|---|---|---|---|
| first series: | ||||
| second series: | ||||
(Observing the large-number ratios at the bottom of each chain, the advantages of prime-factor notation should be obvious.)
Arranging these into a 1-"octave" scale, the way the frets would appear on the fingerboard, gives the following (open string at the bottom):
TABULATION OF SRUTIS IN ANCIENT INDIAN SYSTEM:
| SRUTI | prime-factor "RATIO" | SEMITONES |
|---|---|---|
Below is a graph of this Pythagorean system for one "octave".
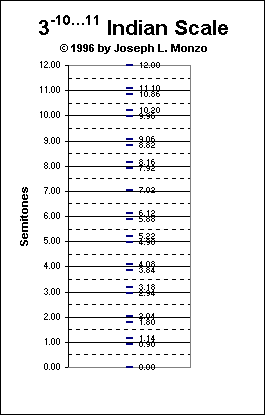
It would have been evident to any musician with even a half-decent ear that 3-8 (only a schisma [= 2 cents] flatter than 5/4) gave a much more consonant "major 3rd" than the "Pythagorean third" 34 [= 81/64]. Similarly for the "minor 3rd" and the "6ths".
Looking closely at the semitone values in the tabulation of srutis, it can be seen that there are 10 pairs of notes a Pythagorean comma [= 24 cents] apart (this is only a schisma larger than the all-important syntonic comma).
The remaining two notes, which appear alone
without a comma-away relative, are
n0 [= 1/1],
the original starting reference tone,
and 31 [= 3/2], its closest
harmonic relation.
In fact, the "schismatic equivalents" provided ancient Indian musicians with the ability to play their 7-tone basic scale in a pseudo-5-limit in at least 10 keys or transpositions.
Arranging the notes into one of my lattice diagrams (modified slightly because of ASCII text limitations), it is easy to see that schismatic equivalence gave a neat box-like structure to the Indian system:
(I give ratios for the notes implied by the tuning and probably in practical or at least theoretical use, and a few of the powers-of-3 for the actual notes tuned, to show schismatic substitution. Semitones are given below the ratio or power. Ratios in parentheses are schismatic substitutions, of notes just beyond either end of the series of 3/2s and which Lentz says were ocasionally used in the tuning.)
MONZO LATTICE DIAGRAM OF
5-LIMIT IMPLICATIONS OF ANCIENT INDIAN SYSTEM:
etc.
/
36
6.12
/
/
35
11.10
/
/
405/25-----81/64----(81/80)
7.94 4.08 0.22
/ / /
/ / /
135/128----27/16-----27/20
0.92 9.06 5.20
/ / /
/ / /
45/32------9/8-------9/5
5.90 2.04 10.18
/ / /
/ / /
15/8-------3/2-------6/5
10.88 7.02 3.16
/ / /
/ / /
5/4-------1/1-------8/5
3.86 0.00 8.14
/ / /
/ / /
5/3-------4/3------16/15
8.84 4.98 1.12
/ / /
/ / /
10/9------16/9------64/45
1.82 9.96 6.10
/ / /
/ / /
(40/27)----32/27----256/135
6.80 2.94 11.08
/
/
3-4
7.92
/
/
3-5
0.90
/
/
3-6
5.88
/
etc.
The basic ascending scale with the syllables sa - ri - ga - ma - pa - dha - ni - (sa) was possible in two forms:
In the sadja-grama scale, pa formed a 3/2 above (or 4/3 below) sa.
In the madhyama-grama scale, pa formed a 3/2 below (or 4/3 above) ri.
Also, in some of the older Indian theoretical treatises, there is the confusing statement that the scale began on the 4th sruti (rather than the open string), which is 32 [= 9/8] in my tabulation above. I have made sense out of this by interpreting the basic scale (with both pas) as follows:
MONZO LATTICE DIAGRAM
OF BASIC SCALE OF ANCIENT INDIAN SYSTEM:
27/16
9.06
PA
of sadja-grama
/
/
9/8
2.04
SA
/
/
15/8--------3/2
10.88 7.02
DHA MA
/ /
/ /
5/4-------1/1
3.86 0.00
RI NI
/ /
/ /
5/3-------4/3
8.84 4.98
PA GA
of madhyama-grama
This gives a sadja-grama basic scale which resembles our "dorian mode", and a madhyama-grama basic scale which resembles our "mixolydian mode".
The whole system gave 10 transpositions (and with the rarely-used two extreme notes, 12) of these basic scales.
Of course, there were many other notes outside these scales, which could be used in a raga as ornamentation or melodic inflection for expressive purposes.
I'm sure, based on what has happened in Western music, that, in a similar way, Indian musicians gradually substituted more and more 5-limit ratios, eventually adding enough of them to find some that were good substitutions of some 7-limit ratios.
If this process continued, they would likewise eventually find 7-limit ratios that were good approximations of some 11- and 13-limit ratios.
But even in the very oldest Indian treatises, which are quite old indeed, a 5-limit system is already implied.
REFERENCES
Donald Lentz, 1961. Tones and Intervals of Hindu Classical Music
University of Nebraska Studies, Lincoln.
Joseph Monzo, 1998. JustMusic: A New Harmony
The following was sent to me in reference to this page:
Date: Thu, 03 May 2001 21:41:33 +0200
From: Martin Spaink
To: monz@juno.com
Hello,
I'm Martin in Amsterdam (1961). I read some of the article, what I could follow, but I also read some misinformed remarks concerning Indian music.
Of course the exact pitch of a paricular tone in a particular raga has always been a point of debate even among musicians. Also, much depends on the tone-quality, the harmonic content. I study a very old style of vocal music through lessons with a great singer from a family that has been keeping this tradition for 20 generations, and they are noted for extreme meticulousness in intonation and timbre-control. But as their manners of verbal expression, understanding, experiencing akouphenomena differ so much from our own, it is not possible to share the information. Westerners such as myself are in a different postion as they can combine both approaches.
The remarks at the bottom of the article about vadi and samvadi are not correct. It means 1st and 2nd most important tones in a certian raga, which can be Sa and Pa (1st and 5th) but this depends on the character of the raga. In raga Shri it is Pa and very low Re, in Multani the raised 4th and high 7 and so fourth.
Have you ever run cooperation with traditionally Indian-educated Westerners?
best wishes, martin spaink
More info on Indian tuning: