An adjective describing the construction of a scale or musical system by successions of 3/2's (just "perfect fifths").
The table below gives the 2,3-monzos and ratios for the chain-of-5ths in pythagorean tuning from 3-12 to 312, normalized to one reference octave and ordered by the exponent of prime-factor 3:
2,3-monzo ratio ~cents tinas [-19 12 > ... 531441 / 524288 .... 23.460 .... 167 [-17 11 > ... 177147 / 131072 ... 521.505 ... 3711 [-15 10 > .... 59049 / 32768 ... 1019.550 ... 7255 [-14 9 > .... 19683 / 16384 .... 317.595 ... 2260 [-12 8 > ..... 6561 / 4096 ..... 815.640 ... 5804 [-11 7 > ..... 2187 / 2048 ..... 113.685 .... 809 [ -9 6 > ...... 729 / 512 ...... 611.730 ... 4353 [ -7 5 > ...... 243 / 128 ..... 1109.775 ... 7897 [ -6 4 > ....... 81 / 64 ....... 407.820 ... 2902 [ -4 3 > ....... 27 / 16 ....... 905.865 ... 6446 [ -3 2 > ........ 9 / 8 ........ 203.910 ... 1451 [ -1 1 > ........ 3 / 2 ........ 701.955 ... 4995 [ 0 0 > ........ 1 / 1 .......... 0 .......... 0 [ 2 -1 > ........ 4 / 3 ........ 498.045 ... 3544 [ 4 -2 > ....... 16 / 9 ........ 996.090 ... 7088 [ 5 -3 > ....... 32 / 27 ....... 294.135 ... 2093 [ 7 -4 > ...... 128 / 81 ....... 792.180 ... 5637 [ 8 -5 > ...... 256 / 243 ....... 90.225 .... 642 [ 10 -6 > ..... 1024 / 729 ...... 588.270 ... 4186 [ 12 -7 > ..... 4096 / 2187 .... 1086.315 ... 7730 [ 13 -8 > ..... 8192 / 6561 ..... 384.360 ... 2735 [ 15 -9 > .... 32768 / 19683 .... 882.405 ... 6279 [ 16 -10 > .... 65536 / 59049 .... 180.450 ... 1284 [ 18 -11 > ... 262144 / 177147 ... 678.495 ... 4828 [ 20 -12 > .. 1048576 / 531441 .. 1176.540 ... 8372
In monzo terminology, such a system would be described as a chain of powers of 3. Pythagoras was given credit in ancient Greece for discovering the properties of musical ratio numbers, with an emphasis on what we would today call powers of 3. (However, it is most likely that this concept of musical tuning was transmitted to the ancient Greeks via scholars who traveled to Babylon, and it is quite possible that the Babylonians got it from the Sumerians, who may have been the first to discover it.)
When the ratios of pitches in a Pythagorean tuning are considered as vectors of exponents prime-factor 3, they may be plotted as a 1-dimensional or "linear" system, as in the example on this lattice diagram:
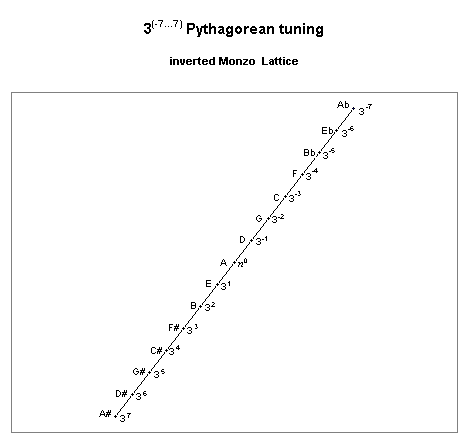
It is easy to see from the lattice that Pythagorean tuning is of the type that may be characterized as a chain. Its generator is the interval which represents 31, and in musical terms it is called a "5th", because it subtends 5 steps of the diatonic scale (described below). Thus, pythagorean tuning is also called a "chain-of-5ths" tuning.
"A" was deliberately chosen as the central reference pitch here, instead of the "C" which is used nearly universally as the reference today. This is primarily for historical reasons, as the notation of musical pitches with letters and accidentals is based on Pythagorean tuning centered on "A", as can be seen in this lattice.
(As the lattice shows, the true point of symmetry is "D". For this reason, "D" was chosen as the reference n by some theorists, such as Fokker. Because the overriding principle in Sumerian art is symmetry, this is also the reason why "D" is the letter-name I use to represent the reference pitch in Monzo, Speculations on Sumerian Tuning.)
For a "5th"-type generator, the smallest MOS which has any useful properties as a musical scale is one of 5 tones -- this is the origin of the ubiquitous "pentatonic scale". The pythagorean pentatonic scale is indicated as a periodicity-block on the lattice diagram shown below, containing the set of pitches extending from C 3-3 to E 31:
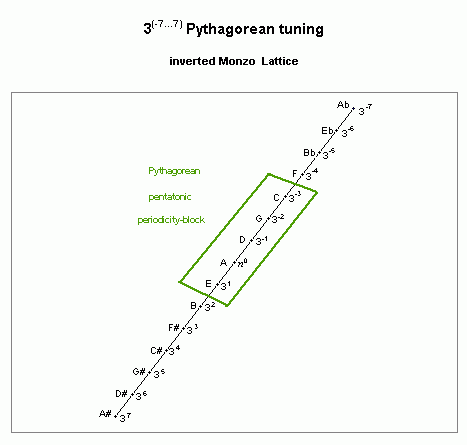
The unison-vector which defines this periodicity block is the interval shown as 5 steps on the lattice (in the negative direction), the limma or pythagorean diatonic semitone:
interval name prime-factor 2,3-monzo ratio ~cents
limma 3-5 [* -5, > 256/243 90.22499567
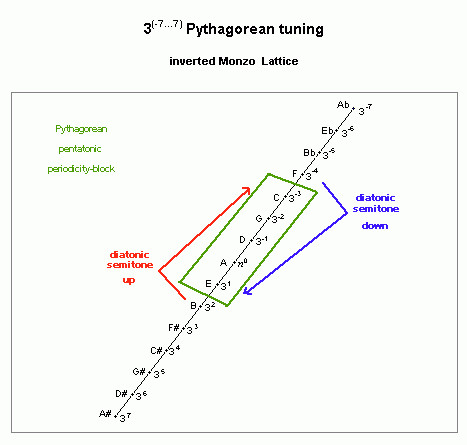
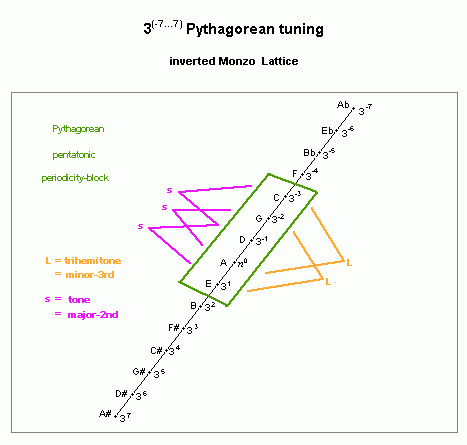
The diatonic semitone is smaller than any of the steps in the scale, thus its role as a unison-vector (in fact, it is the differenc between the two step sizes in this scale). The two step sizes in the pythagorean pentatonic scale are thus the large (L) step, which is a "trihemitone" or minor-3rd, and the small (s) step, which is a "tone" or major-2nd:
interval name prime-factor 2,3-monzo ratio ~cents
L trihemitone 3-3 [* -3, > 32/27 294.1349974
s tone 32 [* 2, > 9/8 203.9100017
Another small interval near the origin which may be used as a unison-vector (albeit larger than the limma), is the "apotome", the pythagorean chromatic semitone, shown as 7 steps on the lattice:
interval name prime-factor 2,3-monzo ratio ~cents
apotome 37 [* 7, > 2187/2048 113.6850061
The periodicity-block formed by this interval contains the 7-tone diatonic scale, indicated on this lattice as the set of pitches from F 3-4 to B 32:
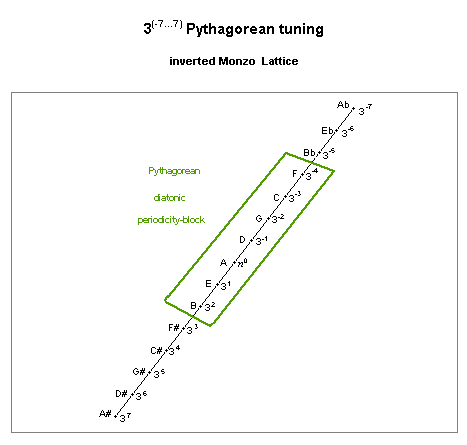
The chromatic semitone, a distance of 7 steps on the lattice, indicates a change from a plain letter-name to one with a sharp or a flat.
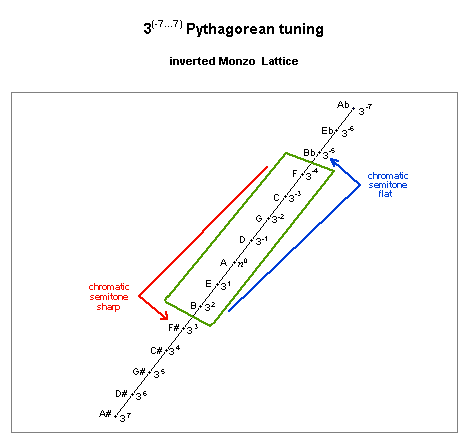
This scale also has two step-sizes:
interval name prime-factor 2,3-monzo ratio ~cents
L tone 32 [* 2, > 9/8 203.9100017
s limma 3-5 [* -5, > 256/243 90.22499567 cents
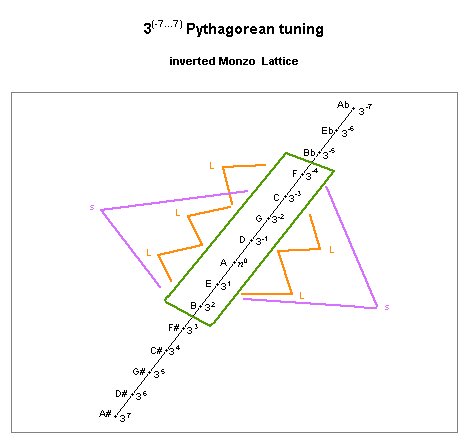
As with the pentatonic scale, the unison-vector defining the diatonic scale is also the difference between the two step sizes in that scale.
Below is an interval-matrix of the Pythagorean diatonic scale, showing the cents values for all intervals appearing between any two tones in this scale:
312, or a distance of 12 steps on the lattice, indicates the pythagorean-comma, the basic interval of enharmonicity in this tuning. This is the distance on the lattice between two pitches which are enharmonically equivalent in the usual 12-EDO tuning, as for example Eb 3-6 and D# 36. These are two slightly different pitches in Pythagorean tuning, about 23 & 1/2 cents apart.
interval name prime-factor 2,3-monzo ratio ~cents
pythagorean-comma 312 [* 12, > 531441/524288 23.46001038
Below is a lattice diagram showing the pythagorean 12-tone chromatic scale as a periodicity-block:
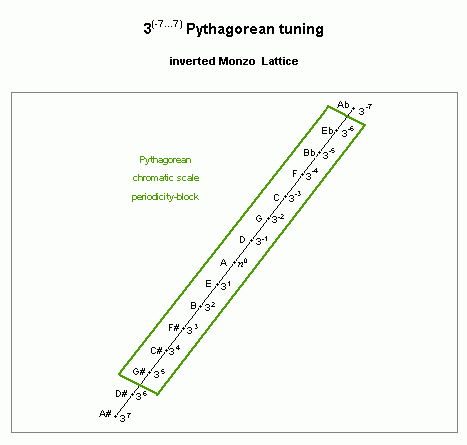
And below is a lattice showing the pythagorean-comma unison-vector which defines this periodicity-block:
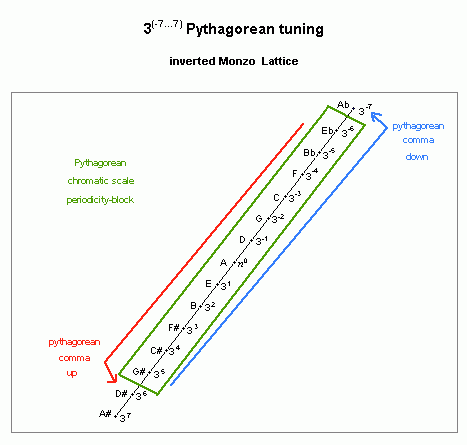
The pythagorean-comma may be tempered out (= made to vanish), by narrowing the width of each "5th" slightly. Since the comma is ~23.46001038 (= ~23 1/2 = ~24) cents, distributing that equally among all twelve "5ths" requires that each "5th" be tempered narrow by ~1.955000865 (= ~1 21/22 = ~2) cents -- this is a measurement called the "grad".
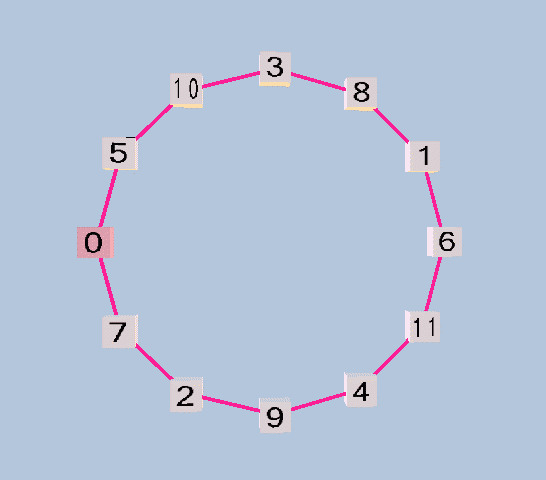
If the pythagorean-comma is tempered out, the result is 12edo, in which the chain of "5ths" closes and becomes a circle. Because the comma vanishes, so does the notational distinction between the sharps and flats: thus, A# = Bb, C# = Db, etc. Many modern composers and theorists, whose use of 12-edo does not reference its older tonal connotations, prefer to use the digits 9 - 11 to represent the degrees of the tuning. The image below shows the degrees of 12edo arranged in a "circle of 5ths".
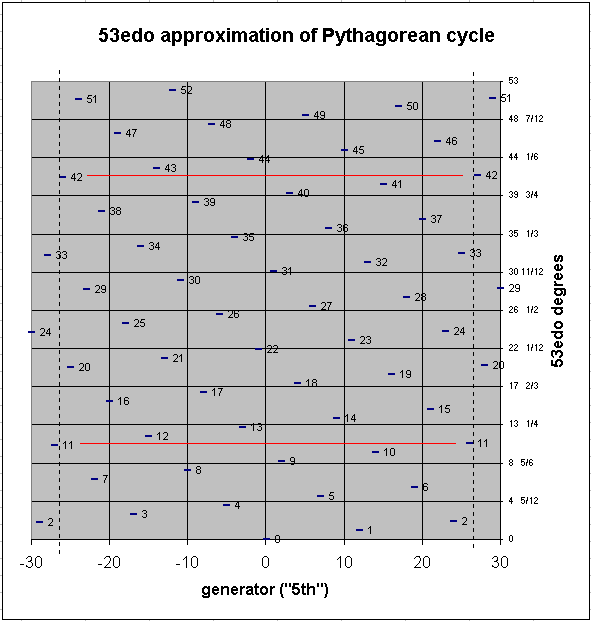
A smaller interval which results from carrying the chain out to 53 degrees is the mercator-comma, 353, which is ~3.615045866 cents, the difference between 4 Pythagorean commas (348) = ~93.84004154 cents and a limma (3-5). Since 4 commas is nearly the same as the limma, and the apotome (37) is one comma larger, this is the origin of the old idea that a "whole-tone" (= limma + apotome) is divided into 4 + 5 = 9 commas. In terms of logarithmic L and s, the octave is composed of 5L + 2s, which equals (5*9)+(2*4) = 45+8 = 53 commas. Thus, the early realization that a 53-tone Pythagorean chain is a nearly-closed system, which would lead to the further realization that 53edo is an excellent approximation of Pythagorean tuning.
The graph below shows the 53-edo approximation of a Pythagorean chain with the arbitrary boundaries of 3(-30...+30), showing that Mercator's comma vanishes. The y-axis shows fractional divisions of 53edo degrees because it is divided into 12 equal parts, for comparison to 12-edo. The black vertical dashed lines show the arbitrary 3(-26...+26) boundaries of a 53edo cycle centered on n0 (if A=n0, this is Bbbbb...Gxx), and the red horizontal lines show the vanishing of Mercator's comma at either end of the cycle if it is continued beyond those boundaries. Assuming Mercator's comma to be below the "margin of error" in interval perception (usually given as ~5 cents), 53edo thus provides an approximation which is audibly indistinguishable from a 53-tone "pure" Pythagorean chain; note that 53-edo actually is a closed tuning and thus gives a circle of 5ths rather than an open-ended chain.
The image below shows the degrees of 53-edo arranged in a "circle of 5ths":
An excellent logarithmic approximation to Pythagorean tuning which does articulate the mercator comma (probably more useful for analysis than as an actual intonation) is 306-edo, where the mercator comma is 1 degree. Below is the same graph, this time in 306-edo, and this time showing Mercator's comma by the red horizontal lines:
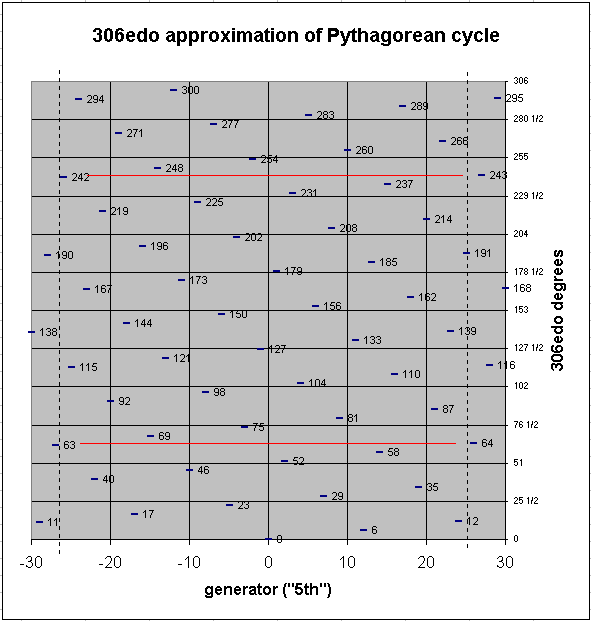
The next point at which the Pythagorean chain nearly closes is 3665, an interval dubbed the satanic comma. It is only ~1/13-cent and thus is completely indistinguishable by any ear.
It can also be seen from these graphs that there is another interval the size of a "comma" at 3-41 = ~19.84496452 cents. In 53-edo it is 1 degree, identical to the Pythagorean comma; in 306-edo it is 5 degrees, one less than the 6 degrees which compose the Pythagorean comma.
Pythagorean tuning can be considered a particular instance of the schismic family of temperaments.
Pertaining to the philosopher Pythagoras.
In tuning theory, Pythagorean refers to a system of tuning by Perfect Fourths, Fifths and Octaves.
Important Pythagorean intervals are:
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.