A member of the meantone family of tunings, and the first temperament of any kind which was described with mathematical exactitude, including a demonstration on how to achieve it physically on a monochord, by Zarlino in 1558 (chapters 42 and 43 of le istitutioni harmoniche , part 2).
2/7-comma meantone belongs to the meantone family because its whole-tone, while not exactly the mean between the two commonly encountered "whole-tones" in just-intonation, does fall between them and is not far from the mean in logarithmic pitch-height.
2/7-comma meantone was described by many authors between 1558 and 1666 --
This seems to indicate that it enjoyed some popularity at least until the late 1600s, by which time 1/4-comma meantone had become widely accepted as the most standarized tuning and the 1/5- and 1/6-comma meantones and various well-temperaments were beginning to gain widespread acceptance.
2/7-comma meantone tuning narrows each 5th in a series of 5ths by 2/7 of a syntonic comma, hence its name. This results in perfect 5ths of approximately 696 cents or 6.96 Semitones. Ascending 5ths will be flatter than just, and descending 5ths will be sharper.
The amount of tempering in 2/7-comma meantone is:
(81/80)-(2/7) = (2-4 * 34 * 5-1)-(2/7) = 2(8/7) * 3(-8/7) * 5(2/7) = ~-6.14465417 cents = ~-6 & 1/7 cents = approximately 1 degree of 195-edo.
So the 2/7-comma meantone 5th -- the generator -- is (3/2) / ((81/80)(2/7)). Using vector addition, that's:
2^ 3^ 5^
[ -1 1 0 ] = 3/2
+ [ 8/7 -8/7 2/7 ] = (2-4345-1)-(2/7) = (81/80)-(2/7)
-----------------------
[ 1/7 -1/7 2/7 ] = 2/7-comma meantone "5th"
= ~695.8103467 cents.
This has the effect of tempering out the syntonic comma so that it vanishes, thus making 4 "5ths" minus 2 "8ves" very close in pitch-height to the just major 3rd:
2,3,5-monzo
[ 4/7 -4/7 8/7 ] = 4 2/7-comma meantone "5ths"
- [ 2 0 0 ] = 2 "8ves"
-----------------------
[-10/7 -4/7 8/7 ] = 2/7-comma meantone "major 3rd" = 5/4 = ~383.2413868 cents.
Assuming octave-equivalence (i.e., the exponents of 2 are irrelevant to the construction of the scale, so i've added 2-1 to the vector here to put the note into the reference "octave"), the next interval in the cycle after the "5th", that of +2 generators, is the whole-tone (major-2nd) 2(-5/7)3(-2/7)5(4/7) = ~191.6206934 cents (... compare with the "true" mean-tone of 1/4-comma meantone, which is ~193.1568569 cents.) If we compare this to the two just intonation whole-tones, subtracting the meantone from the larger pythagorean 9/8 and subtracting the smaller 5-limit 10/9 from the meantone, we find that the meantone "whole-tone" is 4/7-comma narrower than 9:8 and 3/7-comma wider than 10:9 :
2,3,5-monzo
[ -3 2 0 ] = 9/8
- [ -5/7 -2/7 4/7 ] = 2/7-comma mean-tone
-----------------------
[-16/7 16/7 -4/7 ] = ~12.28930834 cents = exactly 4/7 of a syntonic comma.
2^ 3^ 5^
[ -5/7 -2/7 4/7 ] = 2/7-comma mean-tone
- [ 1 -2 1 ] = 10/9
-----------------------
[-12/7 12/7 -3/7 ] = ~9.216981256 cents = exactly 3/7 of a syntonic comma.
Adding those two differences together of course results in 1 syntonic comma, the difference between 10:9 and 9:8.
The 7-tone diatonic scale in 2/7-comma meantone contains only two "step" sizes: the ~191.6206934-cent "whole-tone" described above, between C:D, D:E, F:G, G:A, and A:B, and the ~120.9482665-cent "diatonic semitone" between E:F and B:C:
generator 8ves 2,3,5-monzo ~cents
-1 1 * [-1/7 1/7 -2/7] 504.1896533 "F"
4 - -2 * [ 4/7 -4/7 8/7] 383.2413868 "E"
---------------------------
-5 3 * [-5/7 5/7 -10/7] 120.9482665 2/7-comma meantone diatonic semitone ("minor-2nd")
The Blackwood R value is ~1.584319469.
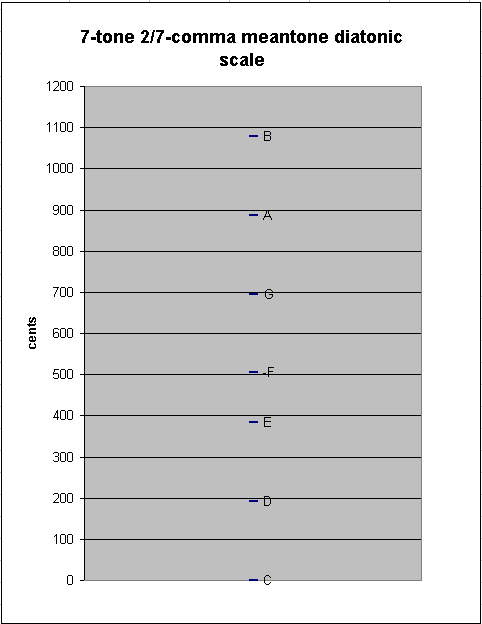
Below is an interval matrix of the intervals available in the 2/7-comma meantone diatonic scale:
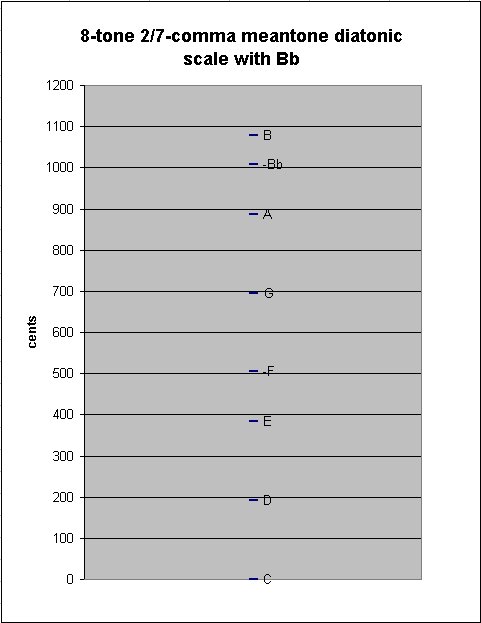
Introducing "Bb" into the scale causes a new between-degree interval to appear: the ~70.67242686-cent "chromatic semitone" between Bb:B. In 2/7-comma meantone this happens to be precisely the just intonation ratio 25:24 :
generator 8ves 2,3,5-monzo ~cents
5 -2 * [ 5/7 -5/7 10/7] 1079.051733 "B"
-2 - 2 * [-2/7 2/7 -4/7] 1008.379307 "Bb"
---------------------------
7 -4 * [ 7/7 -7/7 14/7] 70.67242686 2/7-comma meantone chromatic semitone ("augmented prime")
= 3-1 52 == 25/24
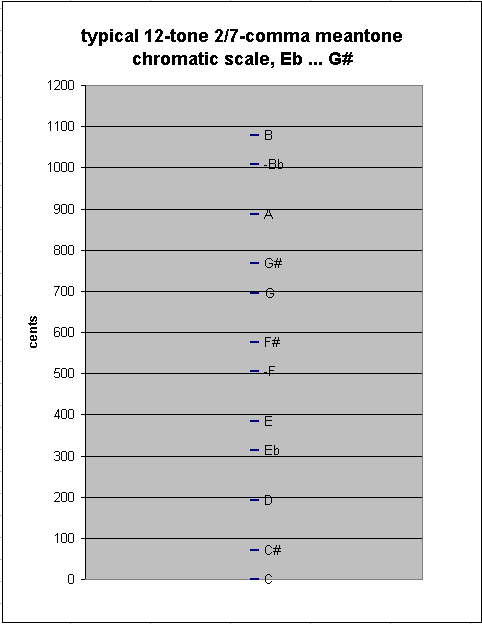
Continuing to add pitches at either end of the chain, we eventually come to the "typical" 12-tone chromatic scale used in Europe during the meantone era, from Eb to G#. This scale has as between-degree intervals only the two sizes of semitones, chromatic and diatonic:
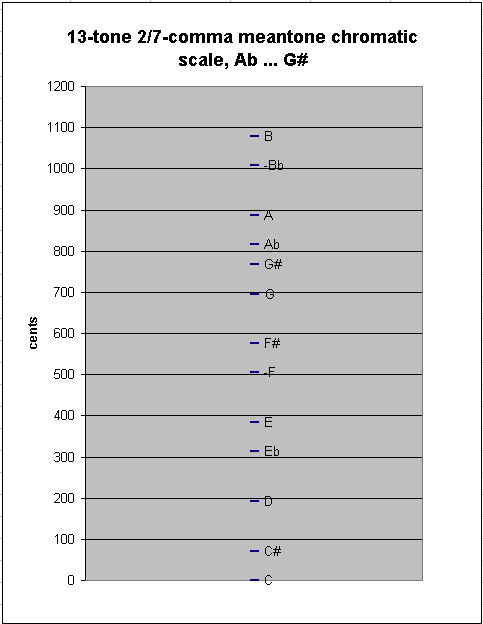
Adding one more note to either end results in another new between-degree interval, of ~50.27583966 cents, as between G#:Ab in my example here:
generator 8ves 2,3,5-monzo ~cents
-4 3 * [-4/7 4/7 -8/7] 816.7586132 "Ab"
8 - -4 * [ 8/7 -8/7 16/7] 766.4827736 "G#"
---------------------------
-12 7 * [12/7 12/7 -24/7] 50.27583966 2/7-comma meantone "great" (enharmonic) diesis ("diminished-2nd")
One may continue to add 6 more notes in this manner without encountering a new step-size; thus, the 19-tone chain of 2/7-comma meantone has between-degree intervals of ~50.27583966 and ~70.67242686 cents:
If a 20th note is added, for example -7 (Cb), there occurs a new, smaller, between-degree interval: ~20.3965872 cents between Cb and B# :
generator 8ves 2,3,5-monzo ~cents
12 -6 * [12/7 -12/7 24/7] 1149.72416 "B#"
-7 - 5 * [-7/7 7/7 -14/7] 1129.327573 "Cb"
---------------------------
19 -11 * [19/7 -19/7 38/7] 20.3965872 2/7-comma meantone small diesis ("magic comma")
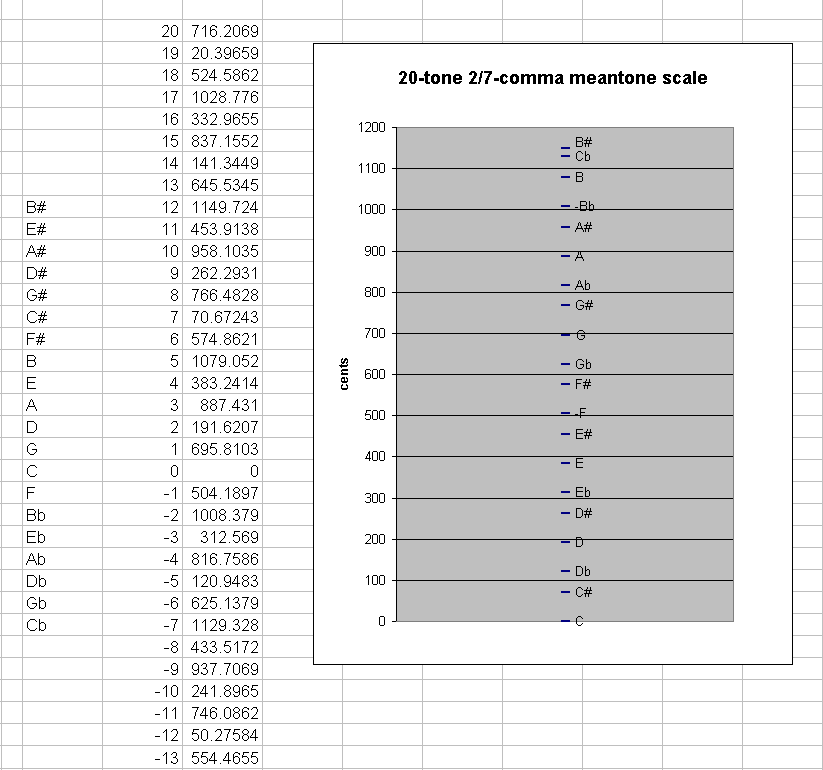
Because this interval is smaller than the syntonic-comma which has already been tempered out, it is rare to find a Renaissance or Baroque composition which uses 2/7-comma meantone in a chain larger than 19 notes.
If one continues to add notes, eventually at the 51st note there will occur another smaller interval, as described below. Extend the chain, for example, to 25 pitches on either side of the origin, so that the -25th generator = "Abbbb" and +25th generator = "Ex#":
generator 8ves 2,3,5-monzo ~cents
-25 15 * [-25/7 25/7 -50/7] 604.7413326 "Abbbb"
25 - -14 * [ 25/7 -25/7 50/7] 595.2586674 "Ex#"
------------------------------
-50 29 * [-50/7 50/7 -100/7] 9.482665255 2/7-comma meantone "septuply-diminished 4th"
~9.482665255 / 50 = ~0.189653305 cents: this amount is the
difference between the 2/7-comma meantone "5th" and the 50edo "5th".
For this reason, 50-edo is audibly indistinguishable from 2/7-comma meantone. 2(29/50) = exactly 696 cents.
Below is a graph showing the 51-tone chain of 2/7-comma meantone. The red line connects the two pitches which are close to each other. If this interval is tempered out, 50edo is the result.
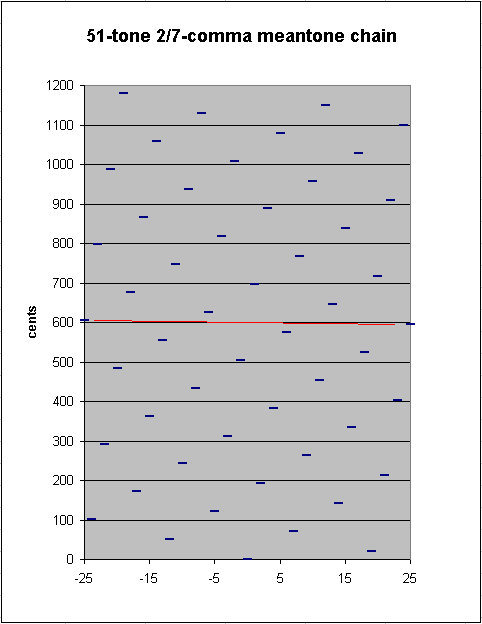
Using vector addition again to compare the 2/7-comma meantone "5th" with the 50-EDO "5th", we get a difference between the two of:
2,3,5-monzo
[ 29/50 0 0 ] = 50-EDO "5th"
- [ 1/7 -1/7 2/7 ] = 2/7-comma meantone "5th"
------------------------
[153/350 1/7 -2/7 ] = 50-EDO "5th" "-" 2/7-comma meantone "5th"
= ~0.189653305 cent = ~1/5 or ~11/58 cent (compare with the last calculation above)
= approximately the superparticular ratio 9129:9128
= about 1/113 syntonic comma
= just a bit over 31 tetradekamus (14mus)
In the 2/7-comma meantone, the generator is 2/7-comma narrower than 3:2. Thus, the +1 generator is 2/7-comma flatter than G 3:2 (= 31) and 5/7-comma sharper than G 40:27 (= 3-351).
The next note in the chain (the +2 generator) is 4/7-comma flatter than 9:8 (= 32). Since 4/7-comma is more than 1/2-comma, it is evident that the +2 generator will be closer to the note a comma flatter than 9:8 (which is the 10:9 ratio = 3-251), namely, 3/7-comma sharper.
(same mapping as that used above)
| interval | generators | Semitones | 50edo degrees | instances | |||||||||||
| diminished 8ve | -7 | 11.29 | 47 | G#:G | F#:F | E:Eb | C#:C | B:Bb | |||||||
| major 7th | +5 | 10.79 | 45 | G:F# | F:E | Eb:D | D:C# | C:B | Bb:A | A:G# | |||||
| minor 7th | -2 | 10.08 | 42 | G#:F# | G:F | F#:E | F:Eb | E:D | D:C | C#:B | C:Bb | B:A | A:G | ||
| augmented 6th | +10 | 9.58 | 40 | Eb:C# | Bb:G# | ||||||||||
| diminshed 7th | -9 | 9.38 | 39 | G#:F | F#:Eb | C#:Bb | |||||||||
| major 6th | +3 | 8.87 | 37 | G:E | F:D | E:C# | Eb:C | D:B | C:A | B:G# | Bb:G | A:F# | |||
| minor 6th | -4 | 8.17 | 34 | G#:E | G:Eb | F#:D | E:C | D:B | C#:A | B:G | A:F | ||||
| augmented 5th | +8 | 7.66 | 32 | F:C# | Eb:B | C:G# | Bb:F# | ||||||||
| wolf 5th | -11 | 7.46 | 31 | G#:Eb | |||||||||||
| 'perfect' 5th | +1 | 6.96 | 29 | G:D | F#:C# | F:C | E:B | Eb:Bb | D:A | C#:G# | C:G | B:F# | Bb:F | A:E | |
| diminished 5th | -6 | 6.25 | 26 | G#:D | F#:C | E:Bb | C#:G | B:F | A:Eb | ||||||
| augmented 4th | +6 | 5.75 | 24 | G:C# | F:B | Eb:A | D:G# | C:F# | Bb:E | ||||||
| 'perfect' 4th | -1 | 5.04 | 21 | G#:C# | G:C | F#:B | F:Bb | E:A | D:G | C#:F# | C:F | B:E | Bb:Eb | A:D | |
| wolf 4th | +11 | 4.54 | 19 | Eb:G# | |||||||||||
| diminished 4th | -8 | 4.34 | 18 | G#:C | F#:Bb | C#:F | B:Eb | ||||||||
| major 3rd | +4 | 3.83 | 16 | G:B | F:A | E:G# | Eb:G | D:F# | C:E | Bb:D | A:C# | ||||
| minor 3rd | -3 | 3.13 | 13 | G#:B | G:Bb | F#:A | E:G | D:F | C#:E | C:Eb | B:D | A:C | |||
| augmented 2nd | +9 | 2.62 | 11 | F:G# | Eb:F# | Bb:C# | |||||||||
| diminished 3rd | -10 | 2.42 | 10 | G#:Bb | C#:Eb | ||||||||||
| major 2nd | +2 | 1.92 | 8 | G:A | F#:G# | F:G | E:F# | Eb:F | D:E | C:D | B:C# | Bb:C | A:B | ||
| minor 2nd | -5 | 1.21 | 5 | G#:A | F#:G | E:F | D:Eb | C#:D | B:C | A:Bb | |||||
| augmented unison | +7 | 0.71 | 3 | G:G# | F:F# | Eb:E | C:C# | Bb:B | |||||||
| unison / 8ve | 0 | 0 or 12 | 0 | G#:G# | G:G | F#:F# | F:F | E:E | Eb:Eb | D:D | C#:C# | C:C | B:B | Bb:Bb | A:A |
It can be seen that a 12-tone subset of meantone contains at least one instance of all intervals from -11 to +11 generators.
the most significant feature of 2/7-comma meantone is that all the ratios of 5 (consonant thirds and sixths) are equally out-of-tune relative to just intonation -- by only 1/7-comma (3.07 cents). any other meantone has some of these intervals differing from just intonation by a greater amount.
[comment from Monzo: 2/7-comma meantone thus forms the point of balance for errors of the two pairs of "ratios of 5" ... see the graph below.]
in the renaissance, these were the most prized consonant intervals, the fourth and fifth being rather "old-fashioned", having been the only recognized stable consonances for the entire history of polyphonic music in the west prior to the renaissance.
[comment from Monzo: because until the renaissance, pythagorean tuning was generally considered to be the standard in Europe. in pythagorean tuning, the "4th" and "5th" are the only consonant intervals, the "3rds" and "6ths" -- which in pythagorean tuning are not "ratios of 5" -- having ratios with quite high numbers.]
of fixed-pitch tunings, only 2/7-comma meantone allows *all* these "new consonances" to sound with such proximity to just intonation, no matter where they may occur in the scale.
hence the appearance of 2/7-comma meantone on the "optimal meantones" table on your meantone page.
Here is a graph showing the error paul is talking about: (the error shown for ratios of 5 is exact, for 7 and 11 only approximate)
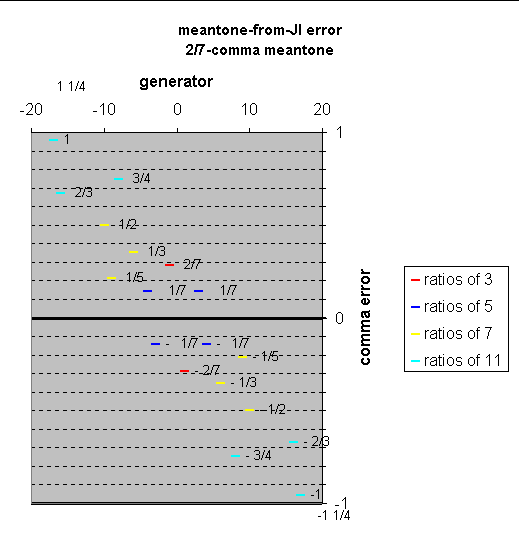
Erlich's point can be very easily seen by looking at the blue plots on the meantone-error applet. A few moments of playing around with that -- especially comparing LucyTuning, 2/7-comma, and 50edo -- will show that 2/7-comma meantone offers both the closest overall approximation to just intonation for the four "ratios of 5", shown on the graph as blue lines, and also the only tuning in which all four of them have exactly the same deviation from just intonation.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.