Private lessons available in person in San Diego, or online using Discord: composition, music-theory, tuning-theory, piano, and all woodwinds (sax, clarinet, flute, bassoon, recorder). Current rates US$ 80 per hour (negotiable). Send an email to: monzojoe2 (AT) gmail. Also please consider making a donation to Tonalsoft using the PayPal button at the bottom of this page. Thank you.
EDO prime error
On this page I present a detailed examination of the amount of absolute error ("absolute" in the sense of ignoring whether the error is positive or negative) of the prime-mapping of several various EDOs of all prime-factors from 3 to 43 (an arbitrarily selected stopping point), using the best approximation of each prime. Note that a composer may deliberately choose to use an EDO as a temperament of JI but employing approximations which are not the closest, but this will not be analyzed here. Also note that prime-factor 2 (the octave) always has zero error, as opposed to TOP tunings where 2 may also be tempered.
Different EDOs approximate JI intervals in different ways. In these listings, errors are given both in cents (as an absolute error measurement) and as a percentage of one degree or "step" of that EDO (as a relative error measurement, that is, relative to that EDO). These latter values are shown on the graphs. Thus, the maximum error on the graph is 50%, which would indicate that the prime-factor lies midway between two neighboring EDO degrees.
Error values tend to cluster into groups -- this clustering is plainly visible on the graphs, and I have also divided the lists accordingly, putting a blank row between clusters.
One of the primary objectives for creating this analysis was to attempt to quantify Ivor Darreg's theory of EDO "moods", wherein Darreg stated that there are no "bad" equal temperaments, each one just has its own particular "mood". Also see Darreg's It Is Time To Release Composers From Hidden Restraints. The analysis here correlates Darreg's theory with the theory of prime-affect.
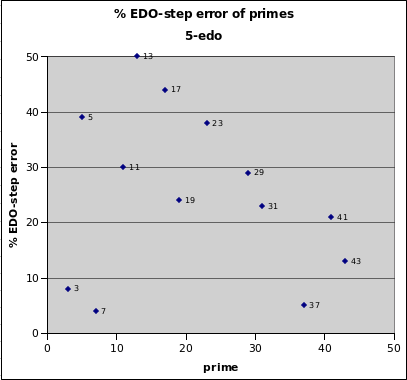
5edo
5edo is the smallest cardinality which is generally perceived as a scale, a type of pentatonic scale. The only prime-factors it represents decently are 3, 7, and 37 -- so it is possible to use it as an approximation to a "no 5s" 7-limit JI, altho the direction of errors for 3 and 7 are opposite.
5edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 5 0 0
7 14 -8.8 -4
37 26 -11.3 -5
3 8 +18.0 +8
43 27 -31.5 +13
41 27 +50.9 +21
31 25 +55.0 +23
19 21 -57.5 -24
29 24 -69.6 -29
11 17 -71.3 -30
23 23 +91.7 +38
5 12 +93.7 +39
17 20 -105.0 -44
13 19 +119.5 +50
|
|
6edo
6edo is the familiar "whole-tone scale" derived from 12edo. Of course, several of its best representations of prime-factors in 43-limit JI are exactly the same as those in 12edo: 5, 7, 11, 13, 23, 29, and 41, which is to say, they are all just as bad as in 12edo, and all of them have less than 25% relative error in 6edo.
6edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 6 0 0
5 14 +13.7 +7
23 27 -28.3 -14
41 32 -29.1 -15
29 29 -29.6 -15
7 17 +31.2 +16
13 22 -40.5 -20
11 21 +48.7 +24
37 31 -51.3 -26
31 30 +55.0 +27
43 33 +88.5 +44
17 25 +95.0 +48
19 25 -97.5 -49
3 10 +98.0 +49
|

|
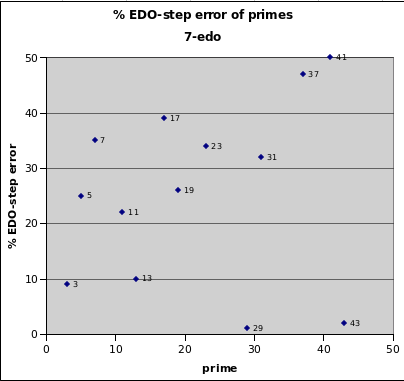
7edo
7edo is the smallest cardinality that can give the impression of a diatonic scale, altho it is lacking the important distinction of the two different step-sizes of all diatonic scales. It is also the smallest cardinality that can be described as a form of meantone. It represents 29 and 43 very well, with relative errors of only 1% and 2% respectively. The only two of the lowest prime-factors which it represents well are 3 and 13. All others in the 43-limit are mediocre and worse.
7edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 7 0 0
29 34 -1.0 -1
43 38 +2.8 +2
3 11 -16.2 -9
13 26 +16.6 +10
11 24 -37.0 -22
5 16 -43.5 -25
19 30 +45.3 +26
31 35 +55.0 +32
23 32 +57.4 +34
7 20 +59.7 +35
17 29 +66.5 +39
37 36 -79.9 -47
41 38 +85.2 +50
|
|
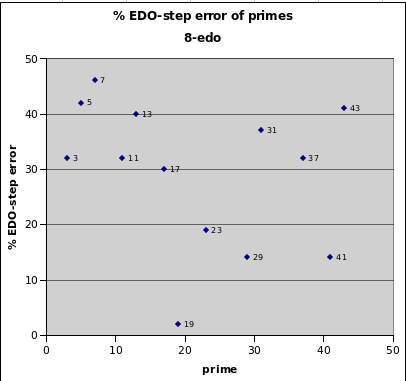
8edo
8edo in the 43-limit represents well only prime-factor 19. It has fair representations of 23, 29, and 41, and mediocre and worse for all other primes in this limit. None of the low primes (3, 5, 7, 11, 13, 17) are represented well.
8edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 8 0 0
19 34 +2.5 +2
29 39 +20.4 +14
41 43 +20.9 +14
23 36 -28.3 -19
17 33 +45.0 +30
3 13 +48.0 +32
11 28 +48.68 +32
37 42 +48.66 +32
31 40 +55.0 +37
13 30 +59.5 +40
43 43 -61.5 -41
5 19 +63.7 +42
7 22 -68.8 -46
|
|
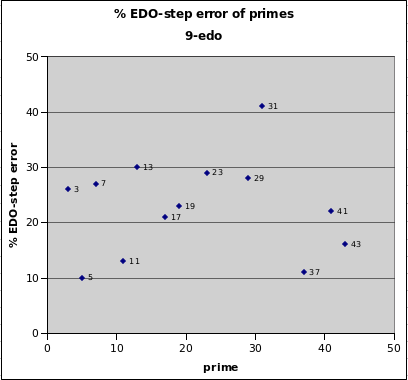
9edo
9edo represents no prime-factors in the 43-limit with less than 10% relative error. Its best representations are of 5, 11, 37, and 43, all under 20%, with another group of 17, 19, and 41 all near 20%, and another group of 3, 7, 13, 23, and 29 all just under 30%, and only 31 being quite poor at 41%. So interestingly, except for 31, its representations of all prime-factors in the 43-limit have relative errors which fall between 10% and 30%.
9edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 9 0 0
5 21 +13.7 +10
37 47 +15.3 +11
11 31 -18.0 -13
43 49 +21.8 +16
17 37 +28.4 +21
41 48 -29.1 -22
19 38 -30.8 -23
3 14 -35.3 -26
7 25 -35.5 -27
29 44 +37.1 +28
23 41 +38.4 +29
13 33 -40.5 -30
31 45 +55.0 +41
|
|
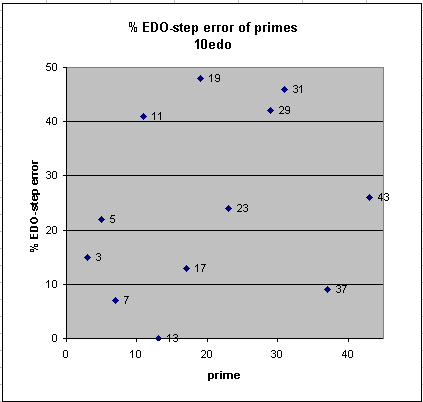
10edo
10edo gives a suberb representation of prime-factor 13 (only ~ -0.5 cent error), and fair-to-mediocre representations of 7 (~ -9 cents error), 37, 17, and 3. It does quite poorly with 5, 11, and 19.
10edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 10 0 0
13 37 -0.5 -0
7 28 -8.8 -7
37 52 -11.3 -9
17 41 +15.0 +13
3 16 +18.0 +15
5 23 -26.3 -22
23 45 -28.3 -24
43 54 -31.5 -26
11 35 +48.7 +41
29 49 +50.4 +42
41 54 +50.9 +42
31 50 +55.0 +46
19 42 -57.5 -48
|
|
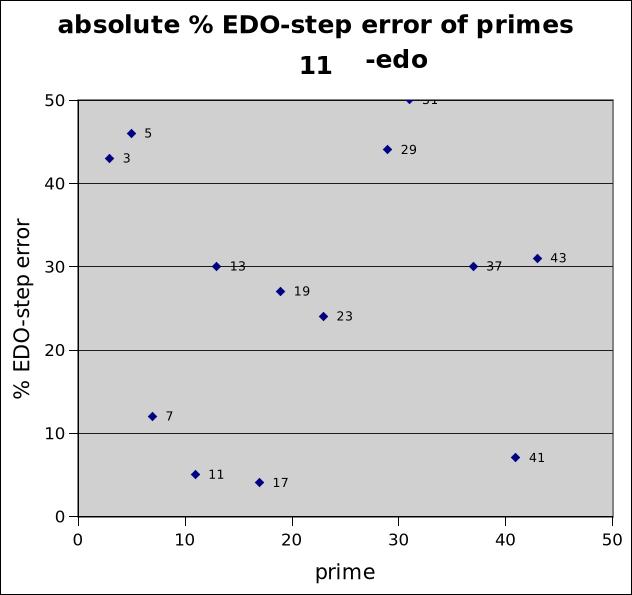
11edo
11edo gives fairly good representations of prime-factors 7, 11, and 17 (~ +13, -6, and +4 cents error, respectively) but does a terrible job with 3 and 5 (~ -47 and +50 cents error).
11edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 11 0 0
17 45 +4.1 +4
11 38 -5.9 -5
41 59 +7.3 +7
7 31 +13.0 +12
23 50 +26.3 +24
19 47 +29.8 +27
13 41 +32.2 +30
37 57 -33.2 -30
43 60 +33.9 +31
3 17 -47.4 -43
29 53 -47.8 -44
5 26 +50.0 +46
31 54 -54.1 -50
|
|
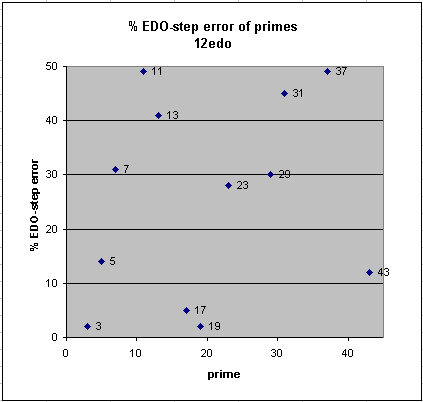
12edo
12edo's best representations of 5 and 43 are mediocre, those of
7, 13, 23 and 29 quite poor, and those of 11, 31, and 37 terrible,
11 and 37 lying basically midway between two 12edo degrees
(50% EDO-step error is the exact midpoint).
12edo is the smallest cardinality which gives representations
of 3 and 5 with low enough error to be perceivable as an approximation
to JI, and at the same time gives the
distinction of the two step-sizes
necessary for the diatonic scales.
Thus, largely because of its practicality, over the course of
four centuries (c. 1600-2000) it became strongly entrenched in Western music.
12edo gives excellent representations of the Pythagorean
12edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 12 0 0
3 19 -2.0 -2
19 51 +2.5 +2
17 49 -5.0 -5
43 65 -11.5 -12
5 28 +13.7 +14
23 54 -28.3 -28
41 64 -29.1 -29
29 58 -29.6 -30
7 34 +31.2 +31
13 44 -40.5 -41
31 59 -45.0 -45
37 63 +48.66 +49
11 42 +48.68 +49
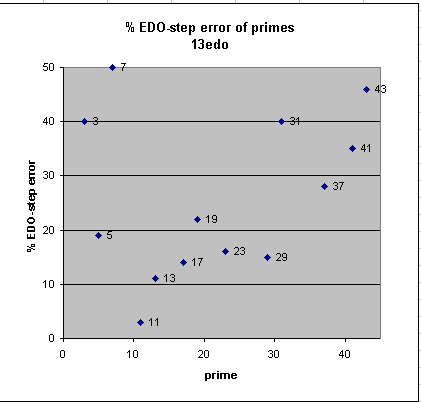
13edo
13edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 13 0 0
11 45 +2.5 +3
13 48 -9.8 -11
17 53 -12.6 -14
29 63 -14.2 -15
5 30 -17.1 -19
23 59 +17.9 +19
19 55 -20.6 -22
37 68 +25.6 +28
41 70 +32.5 +35
3 21 +36.5 +40
31 64 -37.3 -40
43 71 +42.3 +46
7 36 -45.7 -50
|
|
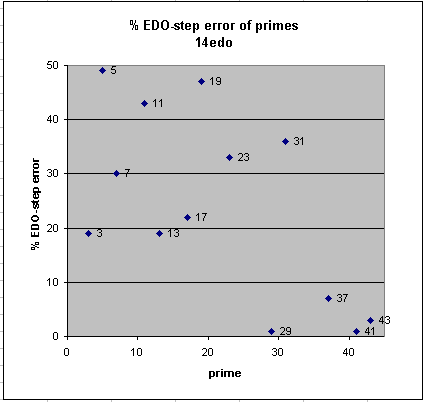
14edo
14edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 14 0 0
41 75 -0.5 -1
29 68 -1.0 -1
43 76 +2.8 +3
37 73 +5.8 +7
3 22 -16.2 -19
13 52 +16.6 +19
17 57 -19.2 -22
7 39 -26.0 -30
23 63 -28.3 -33
31 69 -30.7 -36
11 48 -37.0 -43
19 59 -40.4 -47
5 33 +42.3 +49
|
|
15edo
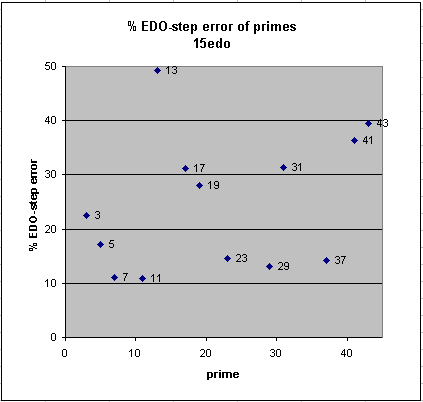
15edo gives fair representations of prime-factors 5, 7, and 11, (as well as higher primes 23, 29, and 37) and a mediocre representation of 3 which is fairly wide at exactly 720 cents. The approximation of 5 is 400 cents, exactly the same one familiar from 12edo. So 15edo could be used as a fair approximation of "no-3s" 11-limit JI (i.e.: 2,5,7,11 prime-factors), and possibly to some degree even of full 11-limit JI (2,3,5,7,11 prime-factors). Note that 15edo does not represent any of the primes in the 43-limit with a relative error of less than 11%.
15edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 15 0 0
11 52 +8.7 +11
7 42 -8.8 -11
29 73 +10.4 +13
37 78 -11.3 -14
23 68 +11.7 +15
5 35 +13.7 +17
3 24 +18.0 +23
19 64 +22.5 +28
17 61 -24.96 -31
31 74 -25.04 -31
41 80 -29.1 -36
43 81 -31.5 -39
13 56 +39.5 +49
|
|
16edo
16edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 16 0 0
19 68 +2.5 +3
7 45 +6.2 +8
5 37 -11.3 -15
43 87 +13.5 +18
13 59 -15.5 -21
31 79 -20.0 -27
29 78 +20.4 +27
41 86 +20.9 +28
11 55 -26.32 -35
37 83 -26.34 -35
3 25 -27.0 -36
23 72 -28.3 -38
17 65 -30.0 -40
|

|
17edo
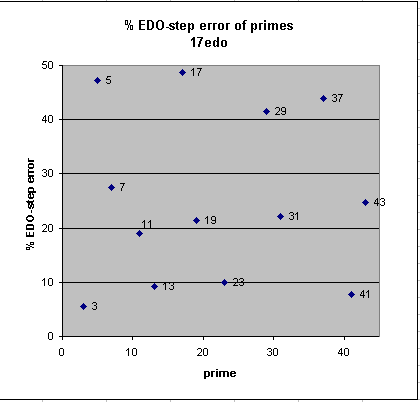
Because of the fact that the 5-limit "3rds" (major-3rd and minor-3rd) are both represented by 5 degrees of 17edo, which is really a "neutral 3rd", it cannot emulate 5-limit tuning well, but rather it functions primarily as a pythagorean tuning, with 4 and 6 degrees being good representations of [-3 0] (i.e., 3-3 = ratio 32:27) and [4 0] (= 34 = ratio 81:64), respectively -- the Pythagorean minor-3rd or "hemiditone", and pythagorean major-3rd> or ditone.
Besides giving a very good representation of the Pythagorean prime-factor 3 (~ +4 cents error), in the 43-prime-limit 17edo also gives decent representations of 13, 23, and 41.
17edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 17 0 0
3 27 +3.9 +6
41 91 -5.5 -8
13 63 +6.5 +9
23 77 +7.0 +10
11 59 +13.4 +19
19 72 -15.2 -21
31 84 -15.6 -22
43 92 -17.4 -25
7 48 +19.4 +27
29 83 +29.2 +41
37 89 +31.0 +44
5 39 -33.4 -47
17 69 -34.4 -49
|
|
18edo
None of 18edo's representations of lower primes is very good, the best error being about 1/5 of an 18edo degree, and most of the lower primes falling nearly midway between two neighboring 18edo degrees. It is thus a good tuning choice to not emulate JI.
18edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 18 0 0
31 89 -11.7 -18
5 42 +13.7 +21
37 94 +15.3 +23
11 62 -18.0 -27
43 98 +21.8 +33
13 67 +26.1 +39
23 81 -28.3 -42
17 74 +28.4 +43
41 96 -29.1 -44
29 87 -29.6 -44
19 76 -30.8 -46
7 51 +31.2 +47
3 29 +31.4 +47
|

|
19edo
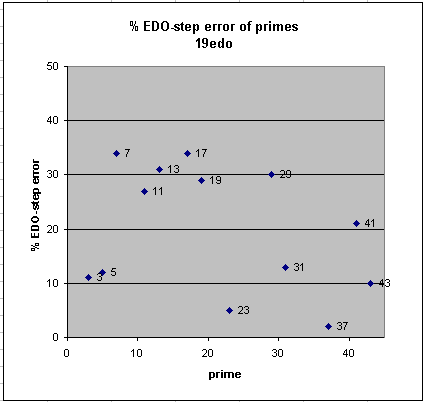
19edo, the next-simplest EDO-meantone after 12edo, does a fairly good job of representing prime-factors 3 and 5, and is mediocre with 7 and 11, but none of the lower primes really has a terrible representation, all primes up to 43 having less than 35% error. Thus, in addition to rendering the entire common-practice repertoire recognizably, it also provides a simple tuning which is fruitful for exploring approximate-JI all the way up to 43-limit.
19edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 19 0 0
37 99 +1.3 +2
23 86 +3.3 +5
43 103 -6.3 -10
3 30 -7.2 -11
5 44 -7.4 -12
31 94 -8.2 -13
41 102 +13.0 +21
11 66 +17.1 +27
19 81 +18.3 +29
29 92 -19.1 -30
13 70 -19.5 -31
17 78 +21.4 +34
7 53 -21.5 -34
|
|
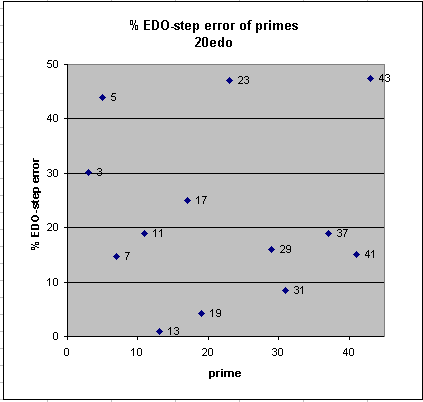
20edo
20edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 20 0 0
13 74 -0.5 -1
19 85 +2.5 +4
31 99 -5.0 -8
7 56 -8.8 -15
41 107 -9.1 -15
29 97 -9.6 -16
11 69 -11.32 -19
37 104 -11.34 -19
17 82 +15.0 +25
3 32 +18.0 +30
5 46 -26.3 -44
23 90 -28.3 -47
43 109 +28.5 +47
|
|
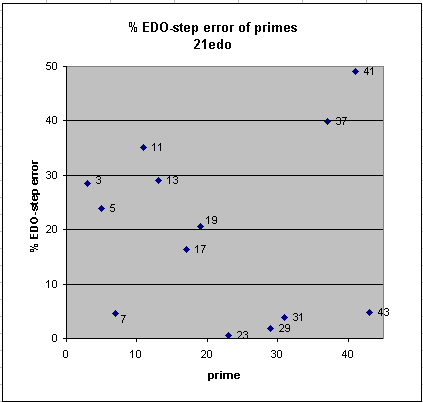
21edo
21edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 21 0 0
23 95 +0.3 +1
29 102 -1.0 -2
31 104 -2.2 -4
7 59 +2.6 +5
43 114 +2.8 +5
17 86 +9.3 +16
19 89 -11.8 -21
5 49 +13.7 +24
3 33 -16.2 -28
13 78 +16.6 +29
11 73 +20.1 +35
37 109 -22.8 -40
41 113 +28.1 +49
|
|
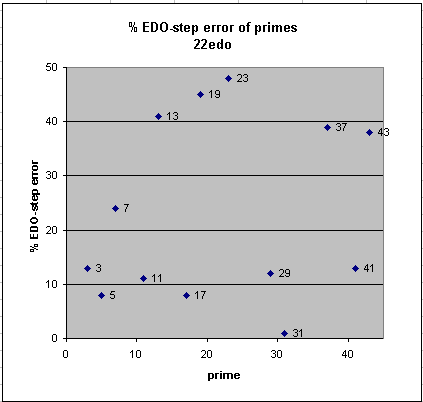
22edo
22edo gives oustanding representations of prime-factors 31 and (beyond the primes considered here) 53; quite good representations of prime-factors 3, 5, 11, 17, 29, and 41, and a mediocre representation of 7.
22edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 22 0 0
31 109 +0.4 +1
17 90 +4.1 +8
5 51 -4.5 -8
11 76 -5.9 -11
29 107 +6.8 +12
3 35 +7.1 +13
41 118 +7.3 +13
7 62 +13.0 +24
43 119 -20.6 -38
37 115 +21.4 +39
13 81 -22.3 -41
19 93 -24.8 -45
23 100 +26.3 +48
|
|
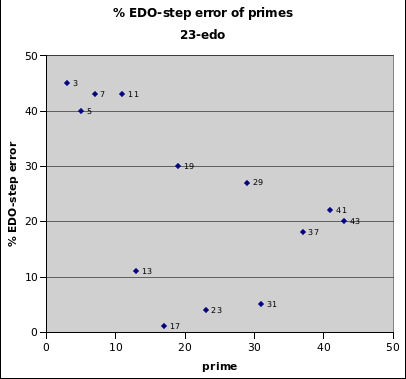
23edo
23edo is generally considered to be a very strange EDO. As can easily be seen on the graph, its worst representations in the 43-limit are the four lowest primes 3, 5, 7, and 11 -- in theory, exactly the ones generally most desired.
23edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 23 0 0
17 94 -0.6 -1
23 104 -2.2 -4
31 114 +2.8 +5
13 85 -5.7 -11
37 120 +9.5 +18
43 125 +10.2 +20
41 123 -11.7 -22
29 112 +13.9 +27
19 98 +15.5 +30
5 53 -21.1 -40
7 65 +22.5 +43
11 80 +22.6 +43
3 36 -23.7 -45
|
|
24edo
The famous "quarter-tone" system. Being simply a halving of the step-size of 12edo, this tuning gives exactly the same representations to JI as some of the prime-mappings of 12-EDO: those of 3, 5, 17, 19, and 43. It gives a significantly better approximation of 7, but in the opposite direction (that is, 24-edo's best representation of 7 is smaller than the actual prime-factor 7, whereas its second-best representation of 7 is exactly the same as 12edo and is larger), therefore, because 24edo's best representation of 5 is larger than the prime, intervals incorporating 24edo's best mappings of prime-factors 5 and 7 (with the errors in opposite directions) do not sound close to those of 7-limit JI. However, 24edo's biggest improvement over 12edo is its excellent mapping of 11, and it also gives significantly better representations of prime-factors 13, 31, and 37.
24edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 24 0 0
11 83 -1.32 -3
37 125 -1.34 -3
3 38 -2.0 -4
19 102 +2.5 +5
17 98 -4.955 -10
31 119 +4.964 +10
13 89 +9.5 +19
43 130 -11.5 -23
5 56 +13.7 +27
7 67 -18.8 -38
29 117 +20.4 +41
41 129 +20.9 +42
23 109 +21.7 +43
|

|
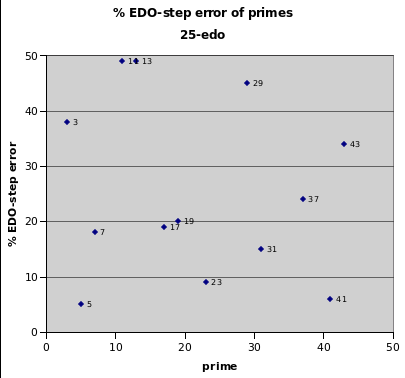
25edo
25edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 25 0 0
5 58 -2.3 -5
41 134 +2.9 +6
23 113 -4.3 -9
31 124 +7.0 +15
7 70 -8.8 -18
17 102 -9.0 -19
19 106 -9.5 -20
37 130 -11.3 -24
43 136 +16.5 +34
3 40 +18.0 +38
29 121 -21.6 -45
11 86 -23.3 -49
13 93 +23.5 +49
|
|
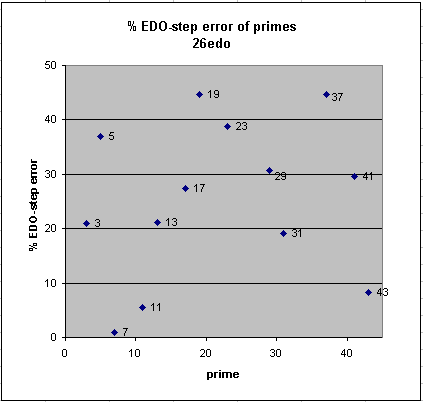
26edo
26edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 26 0 0
7 73 +0.4 +1
11 90 +2.5 +5
43 141 -3.8 -8
31 129 +8.8 +19
3 41 -9.6 -21
13 96 -9.8 -21
17 106 -12.6 -27
41 139 -13.7 -30
29 126 -14.2 -31
5 60 -17.1 -37
23 118 +17.9 +39
37 135 -20.57 -45
19 110 -20.59 -45
|
|
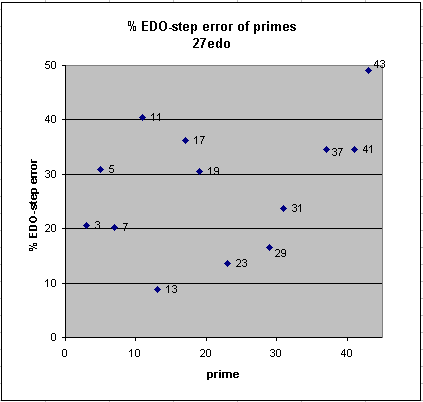
27edo
27edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 27 0 0
13 100 +3.9 +9
23 122 -6.1 -14
29 131 -7.4 -17
7 76 +9.0 +20
3 43 +9.2 +21
31 134 +10.5 +24
19 115 +13.6 +31
5 63 +13.7 +31
37 141 +15.3 +34
41 145 +15.4 +35
17 110 -16.1 -36
11 93 -18.0 -40
43 147 +21.8 +49
|
|
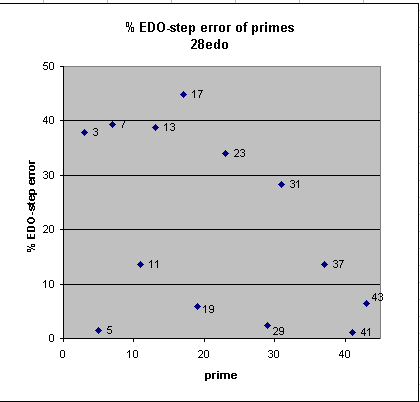
28edo
28edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 28 0 0
41 150 -0.5 -1
5 65 -0.6 -1
29 136 -1.0 -2
19 119 +2.5 +6
43 152 +2.8 +6
37 146 +5.799 +14
11 97 +5.825 +14
31 139 +12.1 +28
23 127 +14.6 +34
3 44 -16.2 -38
13 104 +16.6 +39
7 79 +16.9 +39
17 114 -19.2 -45
|
|
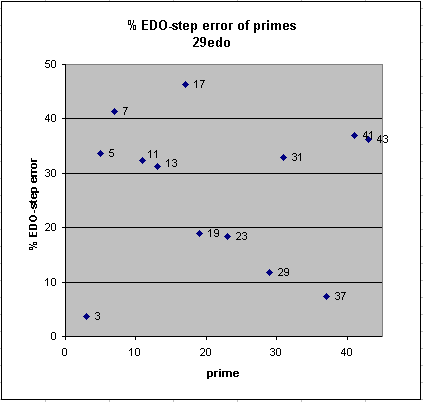
29edo
29-edo gives an excellent mapping of prime-factor 3, and is thus a good representation of pythagorean tuning.
29edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 29 0 0
3 46 +1.5 +4
37 151 -3.1 -7
29 141 +4.9 +12
23 131 -7.6 -18
19 123 -7.9 -19
13 107 -12.9 -31
11 100 -13.4 -32
31 144 +13.6 +33
5 67 -13.9 -34
43 157 -15.0 -36
41 155 -15.3 -37
7 81 -17.1 -41
17 119 +19.2 +46
|
|
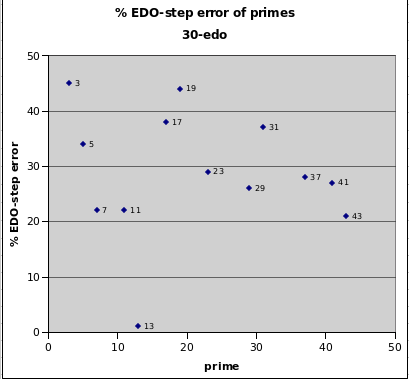
30edo
30edo is very strange in the 43-limit. It gives a superb representation of only prime-factor 13; all other primes from 3 to 43 have more than 20% error, and their errors are fairly evenly distributed.
30edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 30 0 0
13 111 -0.5 -1
43 163 +8.5 +21
11 104 +8.7 +22
7 84 -8.8 -22
29 146 +10.4 +26
41 161 +10.9 +27
37 156 -11.3 -28
23 136 +11.7 +29
5 70 +13.7 +34
31 149 +15.0 +37
17 123 +15.0 +38
19 127 -17.5 -44
3 48 +18.0 +45
|
|
31edo
31edo is historically important as a very good approximation to 1/4-comma meantone. Among the lowest primes, it gives excellent representations of prime-factors 5 (~ 3/4 cent error) and 7 (~ 1 cent error), a passable representation of 3, and mediocre representation of 11 and 23; all of these mappings except that of 5 are smaller in size than the actual primes. Note that it also gives mediocre representations of 13, 17, and 19, but those are in the opposite direction, larger than the primes.
31edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 31 0 0
5 72 +0.8 +2
7 87 -1.1 -3
41 166 -3.3 -8
3 49 -5.2 -13
43 168 -8.3 -21
23 140 -8.9 -23
11 107 -9.4 -24
13 115 +11.1 +29
17 127 +11.2 +29
19 132 +12.2 +31
29 151 +15.6 +40
31 154 +16.3 +42
37 161 -19.1 -49
|

|
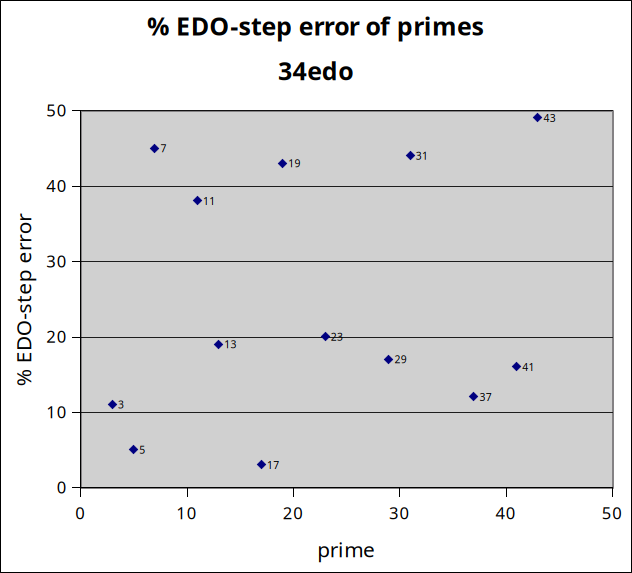
34edo
34edo gives a good approximation of prime-factor 3 and a very good approximation of 5. For this reason it has been used as an EDO representation of 5-limit JI. 17 is its best approximation among the lower primes, and 13, 23, 29, 37, and 41 are mediocre but all with less than 20% error. Notably, 7, 11, and 19 are poorly represented.
34edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 34 0 0
17 139 +0.9 3
5 79 +1.9 5
3 54 +3.9 11
37 177 -4.3 12
41 182 -5.5 16
29 165 -6.05 17
13 126 +6.5 19
23 154 +7.02 20
11 118 +13.4 38
19 144 -15.2 43
31 168 -15.6 44
7 95 -15.9 45
43 184 -17.4 49
|
|
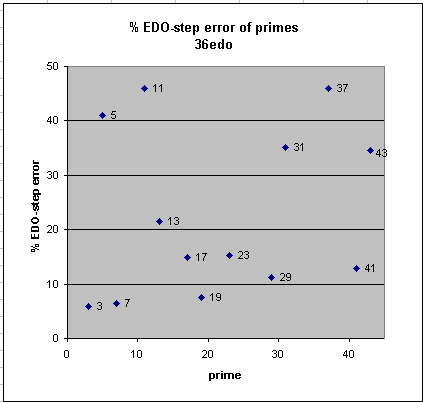
36edo
Similarly to 24edo, 36edo has been advocated as a fairly easy means of exploring microtonality by simply dividing each degree of 12edo into 3 equal parts. Again, as with 24edo, some of its best representations of 43-limit JI are exactly the same as those of 12edo: prime-factors 3, 5, 17, 19, and 43 -- thus, its approximation of 5-limit JI gives no advantage over 12edo. However, 36edo offers a superb representation of prime-factor 7, making it a much better approximation of 7-limit JI. And it provides significantly better representations than 12edo of prime-factors 13, 23, 29, and 41.
As a side note, not shown in this analysis: while 12\36 (12 degrees of 36) is the best mapping of 5 (exactly 400 cents, same as 12edo), the second-best mapping of 5, to 11\36, gives an absolute error in cents larger than anything in the table below, and a relative error of 59%, but puts the error of 5 in the same negative direction as with those of 3 and 7, and provides an alternate flavor for approximations of 5- and especially 7-limit JI. This tuning is known as the breed 36c, which uses a "wart" in its name, the wart being the letter "c" as the third letter of the alphabet designating the third prime-factor 5, and the single occurence of the letter indicating that it is the second-best mapping of that prime.
36edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 36 0 0
3 57 -2.0 -6
7 101 -2.2 -6
19 153 +2.5 +7
29 175 +3.8 +11
41 193 +4.3 +13
17 147 -5.0 -15
23 163 +5.1 +15
13 133 -7.2 -22
43 195 -11.5 -35
31 178 -11.7 -35
5 84 +13.7 +41
37 188 +15.32 +46
11 125 +15.35 +46
|
|
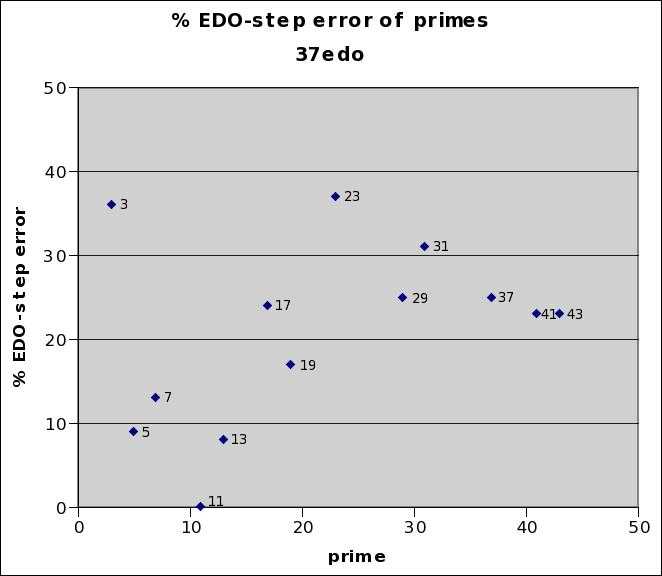
37edo
37edo is the first cardinality which gives essentially no error for a prime-mapping other than 2 in the 43-limit: the relative error for 11 is +0.1%. It also gives excellent representations of prime-factors 5, 7, and 13. It is thus a great approximation of "no 3s" 13-limit JI. Its representation of prime-factor 3 is quite mediocre, with a relative error of more than 1/3 of a step of 37edo.
37edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 37 0 0
11 128 +0.03 +0.1
13 137 +2.7 +8
5 86 +2.9 +9
7 104 +4.15 +13
19 157 -5.6 -17
41 198 -7.44 -23
43 201 +7.40 +23
17 151 -7.7 -24
29 180 +8.3 +25
37 193 +8.1 +25
31 183 -9.9 -31
3 59 +11.6 +36
23 167 -12.1 -37
|
|
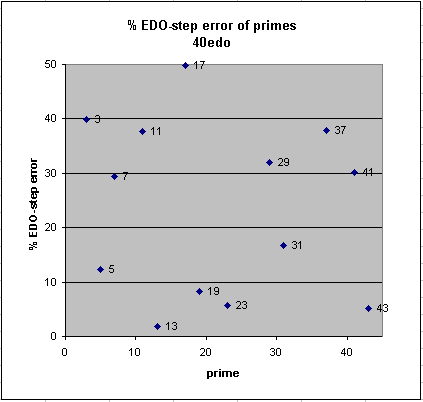
40edo
40edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 40 0 0
13 148 -0.5 -2
43 217 -1.5 -5
23 181 +1.7 +6
19 170 +2.5 +8
5 93 +3.7 +12
31 198 -5.0 -17
7 112 -8.8 -29
41 214 -9.1 -30
29 194 -9.6 -32
11 138 -11.32 -38
37 208 -11.34 -38
3 63 -12.0 -40
17 163 -15.0 -50
|
|
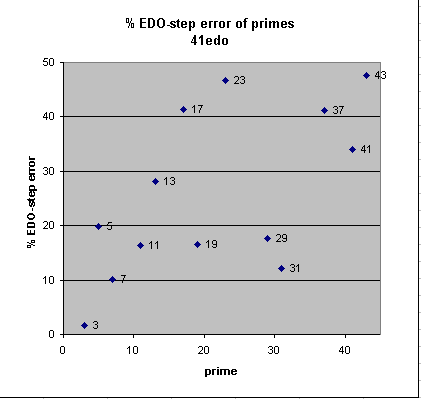
41edo
41edo gives a superb representation of the Pythagorean prime-factor 3, and decent representations of 5, 7, and 11. It is thus a very good approximation of 11-limit JI, and also gives good representations of prime-factors 19, 29, and 31.
41edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 41 0 0
3 65 +0.5 +2
7 115 -3.0 -10
31 203 -3.6 -12
11 142 +4.8 +16
19 174 -4.8 -17
29 199 -5.2 -18
5 95 -5.8 -20
13 152 +8.3 +28
41 220 +10.0 +34
37 214 +12.07 +41
17 168 +12.12 +41
23 185 -13.6 -47
43 222 -14.0 -48
|
|
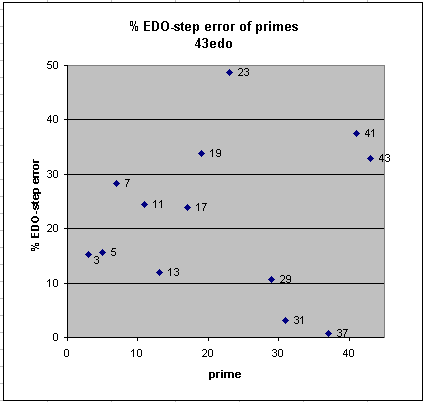
43edo
43-EDO is historically important as an approximation of 1/5-comma meantone.
43edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 43 0 0
37 224 -0.2 -1
31 213 -0.8 -3
29 209 +3.0 +11
13 159 -3.3 -12
3 68 -4.3 -15
5 100 +4.4 +16
17 176 +6.7 +24
11 149 +6.8 +24
7 121 +7.9 +28
43 233 -9.2 -33
19 183 +9.5 +34
41 230 -10.5 -37
23 195 +13.6 +49
|
|
see also: meride
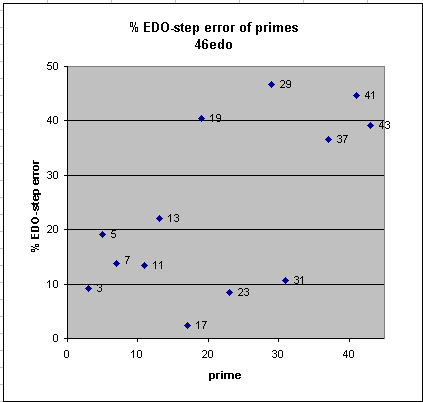
46edo
46edo provides excellent approximations to basic intervals in the 11-limit, as can be seen on the equal-temperament gallery page, and also an excellent representation of 17 and good representations of 13, 23, and 31. All 17-limit factors have less than 6 cents absolute error, and the 13-limit factors cluster between 8% and 22% relative error.
46edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 46 0 0
17 188 -0.6 -2
23 208 -2.2 -8
3 73 +2.4 +9
31 228 +2.8 +11
11 159 -3.5 -13
7 129 -3.6 -14
5 107 +5.0 +19
13 170 -5.7 -22
37 240 +9.5 +37
43 250 +10.2 +39
19 195 -10.6 -40
41 246 -11.7 -45
29 223 -12.2 -47
|
|
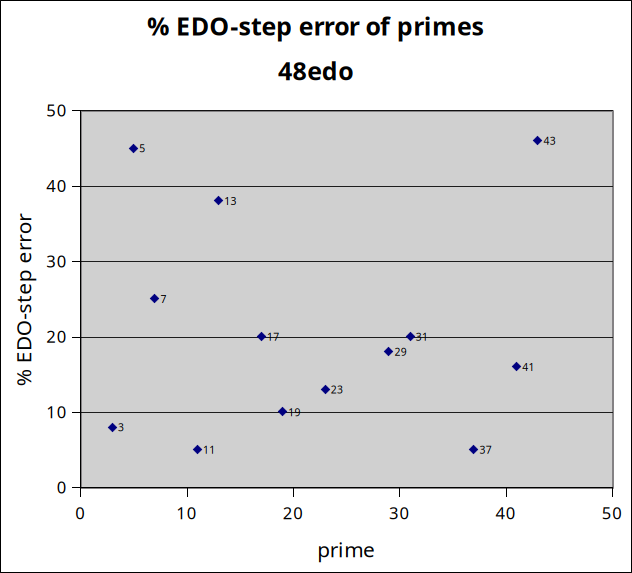
48edo
48edo provides excellent approximations to prime-factors 37 and 11, good approximations of 3, 19, and 23, and fair representations of 23, 41, 29, 17, and 31. Its approximation of 7 is mediocre, and those of 13, 5, and 43 are poor.
48edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 48 0 0
37 250 -1.3 -5.4
11 166 -1.3 -5.3
3 76 -2.0 -8
19 204 +2.5 +10
23 217 -3.3 -13
41 257 -4.1 -16
29 233 -4.6 -18
17 196 -5.0 -19.8
31 238 +5.0 +19.9
7 135 +6.2 +25
13 178 +9.5 +38
5 111 -11.3 -45
43 260 -11.5 -46
|
|
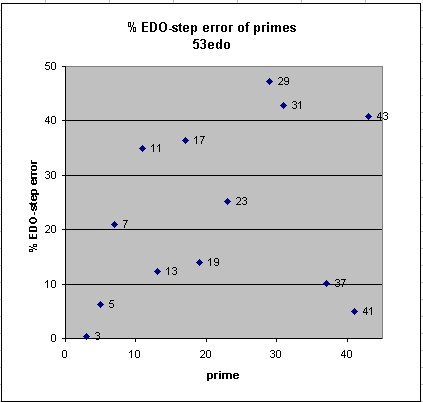
53edo
53edo is the next cardinality (after 37edo) which presents a negligible error in the 43-limit: it gives an outstanding representation of the Pythagorean prime-factor 3 (~ 1/15 cent error), with a relative error of only -0.3%. It also provides a very good representation of 5 (~ 1.4 cents error), and mediocre ones of 7 and 11. It is thus an outstanding approximation to pythagorean (3-limit) tuning, and a extremely good approximation to 5-limit JI, and has been advocated often (particularly in the late 1800s and early 1900s) as a means for expansion of the tonal palette beyond 12edo, and is still advocated in the early 21st century by many microtonalists as an "ultimate tuning".
53edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 53 0 0
3 84 -0.1 -0.3
41 284 +1.1 +5
5 123 -1.4 -6
37 276 -2.3 -10
13 196 -2.8 -12
19 225 -3.2 -14
7 149 +4.8 +21
23 240 +5.7 +25
11 183 -7.9 -35
17 217 +8.3 +36
43 288 +9.2 +41
31 263 +9.7 +43
29 257 -10.7 -47
|
|
55edo
The striking thing to observe about 55edo is that, despite its status as a "standard" tuning during the meantone era (see my webpage on Mozart's Tuning), none of its lower-prime representations is especially good in terms of relative error: the best approximations are about 1/5 of a 55edo degree off.
55edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 55 0 0
3 87 -3.8 -17
29 267 -4.12 -19
17 225 +4.14 +19
23 249 +4.5 +20
11 190 -5.9 -27
5 128 +6.4 +29
41 295 +7.3 +33
19 234 +7.9 +36
7 154 -8.8 -40
43 298 -9.7 -44
13 204 +10.38 +48
37 287 +10.47 +48
31 272 -10.49 -48
|

|
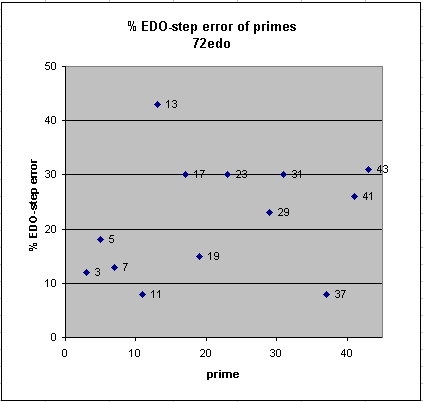
72edo
72edo gives a very good representation of 11-limit JI, with errors of prime-factors 3, 5, 7, and 11 (as well as 37 and 19) all under 20%. Also, because the errors of 3, 5, and 7 are all in the same direction (negative), intervals among these primes tend to sound very much like just intervals. 72edo also gives fairly good representations of many of the higher prime-factors, unfortunately giving a very poor approximation to 13.
The fact that 72edo's approximations do not temper out so many important 5-limit intervals means that, even tho it is not as accurate as the lower-cardinality 53edo in representing the entire 5-limit lattice, its structure does emulate so many of the important lower-limit JI commas that in a systemic sense it is easily perceived as a good approximation of 11-limit JI. It was formulated by Joseph Monzo as a good simplified version of HEWM notation.
72edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 72 0 0
11 249 -1.32 -8
37 375 -1.34 -8
3 114 -1.96 -12
7 202 -2.16 -13
19 306 +2.49 +15
5 167 -2.98 -18
29 350 +3.76 +23
41 386 +4.27 +26
17 294 -4.96 -30
31 357 +4.96 +30
23 326 +5.06 +30
43 391 +5.15 +31
13 266 -7.19 -43
|
|
81edo
81-EDO is of interest as a very close approximation to golden-meantone. It gives a very good approximation of prime-factor 5 and some other higher primes (17, 19, 37, 41), and it represents 11 and 13 with middling accuracy, but as with many meantones its approximation of 3 is quite mediocre.
81edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 81 0 0
37 422 +0.51 +3
41 434 +0.57 +4
5 188 -1.13 -8
19 344 -1.22 -8
17 331 -1.25 -8
11 280 -3.17 -21
13 300 +3.92 +26
31 401 -4.29 -29
3 128 -5.66 -38
7 227 -5.86 -40
23 366 -6.05 -41
43 440 +7.00 +47
29 393 -7.35 -50
|

|
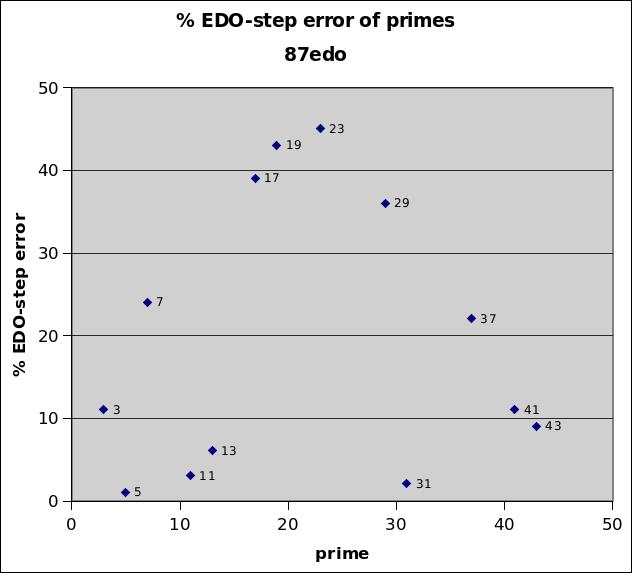
87edo
87edo is a very good approximation to 13-limit JI, giving excellent representations of prime-factors 3, 5, 11, and 13, and a mediocre representation of 7 that is still not too bad. It also gives excellent representations of primes 31, 41, and 43, and a mediocre 37.
87edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 87 0 0
5 202 -0.11 -1
31 431 -0.21 -2
11 301 +0.41 +3
13 322 +0.85 +6
43 472 -1.17 -9
41 466 -1.48 -11
3 138 +1.49 +11
37 453 -3.07 -22
7 244 -3.31 -24
29 423 +4.91 +36
17 356 +5.39 +39
19 370 +5.94 +43
23 394 +6.21 +45
|
|
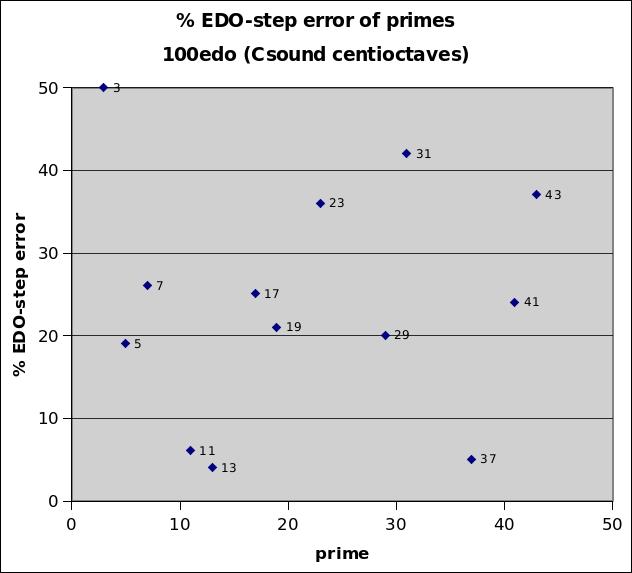
100edo
100edo is significant as one of the built-in microtonal tunings in the Csound music programming language, making it very easy to compose pieces in 100edo in Csound. The only prime-factors within the 43-limit at which it excels are 11, 13, and 37; all the rest are near or above 20% relative error.
100edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 100 0 0
13 370 -0.53 -4
37 521 +0.66 +5
11 346 +0.68 +6
5 232 -2.31 -19
29 486 +2.42 +20
19 425 +2.49 +21
41 536 +2.94 +24
17 409 +3.04 +25
7 281 +3.17 +26
23 452 -4.27 -36
43 543 +4.48 +37
31 495 -5.04 -42
3 158 -5.96 -50
|
|
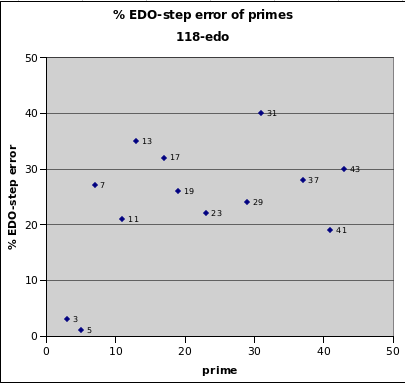
118edo
118edo give an outstanding approximation of 5-limit JI, with relative errors below 4% for prime-factors 3 and 5. Errors for all the rest of the primes within the 43-limit are fairly evenly distributed between 19% and 35%, with prime 31 the only outlier at 40%.
118edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 118 0 0
5 274 +0.13 +1
3 187 -0.26 -3
41 632 -1.94 -19
11 408 -2.17 -21
23 534 +2.23 +22
29 573 -2.46 -24
19 501 -2.60 -26
7 331 -2.72 -27
37 615 +2.89 +28
43 640 -3.04 -30
17 482 -3.26 -32
13 437 +3.54 +35
31 585 +4.12 +40
|
|
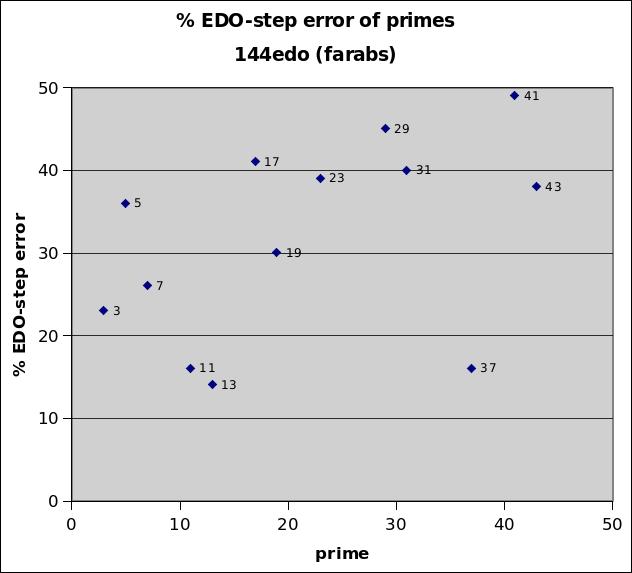
144edo
144edo does not give any especially good mappings to prime-factors within the 43-limit, with all of its relative errors at 14% and above. Its main interest is in its extreme divisiblity: it can function as 18 bike-chains of 8edo, 16 bike-chains of 9edo, 12 bike-chains of 12edo, 8 bike-chains of 18edo, 6 bike-chains of 24edo, 4 bike-chains of 36edo, 3 bike-chains of 48edo, or 2 bike-chains of 72edo. It was used by Dan Stearns and Joseph Monzo as a notation, not as an actual tuning, with one extra accidental as a supplement to 72-edo HEWM, to indicate subtleties smaller than those available in 72edo.
144edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 144 0 0
13 533 +1.14 +14
11 498 -1.32 -16
37 750 -1.34 -16
3 228 -1.96 -23
7 404 -2.16 -26
19 612 +2.49 +30
5 334 -2.98 -36
43 781 -3.18 -38
23 651 -3.27 -39
31 713 -3.37 -40
17 589 +3.38 +41
29 700 +3.76 +45
41 771 -4.06 -49
|
|
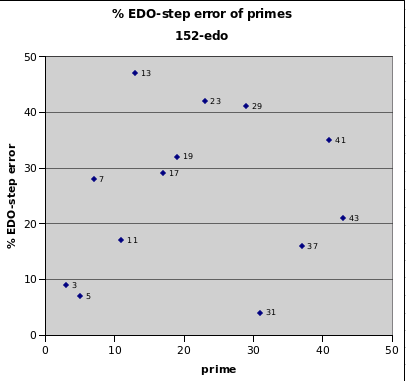
152edo
152edo gives a decent approximation of 5-limit JI, with relative errors below 10% for prime-factors 3 and 5, and also for 31. Errors for 11, 37, and 41 are all mediocre at around 20%, and for all the rest of the primes within the 43-limit are errors are above 28%. Its main interest is that it can work as an adaptive-JI in the form of 8 bike-chains of 19edo.
152edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 152 0 0
31 753 -0.30 -4
5 353 +0.53 +7
3 241 +0.68 +9
37 792 +1.29 +16
11 526 +1.31 +17
43 825 +1.64 +21
7 427 +2.23 +28
17 621 -2.32 -29
19 646 +2.49 +32
41 814 -2.75 -35
29 738 -3.26 -41
23 688 +3.30 +42
13 562 -3.69 -47
|
|
161edo
161edo is included here only because the graph exhibits an interesting pattern in the errors, where about half of the primes have fairly low error and the other half higher, in an almost alternating pattern, and the lowest primes having the lowest error while the amount of error increases with the prime series thru the 43-limit.
161edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 171 0 0
7 452 +0.12 +2
11 557 +0.23 +3
17 658 -0.61 -8
19 684 +0.62 +8
29 782 -1.01 -13
3 255 -1.33 -18
5 374 +1.26 +17
13 596 +1.71 +23
37 839 +2.07 +28
23 728 -2.19 -29
43 874 +2.77 +37
31 798 +2.79 +37
41 863 +3.24 +43
|

|
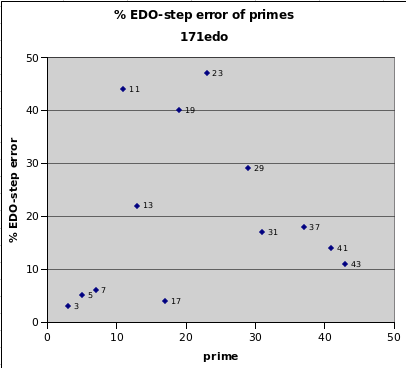
171edo
171edo was advocated by German theorist Martin Vogel in many of his numerous books as an excellent approximation to 7-limit JI. Its prime-mappings to 3, 5, 7, and 17 have very low error, and it was used by Vogel as an integer unit of measurement for 7-limit JI. It can also function as 9 bike-chains of 19-edo, allowing its use as an adaptive-JI.
171edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 171 0 0
3 271 -0.20 -3
17 699 +0.31 +4
5 397 -0.35 -5
7 480 -0.40 -6
43 928 +0.76 +11
41 916 -0.99 -14
31 847 -1.18 -17
37 891 +1.29 +18
13 633 +1.58 +22
29 831 +2.00 +29
19 726 -2.78 -40
11 592 +3.07 +44
23 774 +3.30 +47
|
|
205edo
205edo is a tuning used by H-Pi instruments for its flagship microtonal keyboard the Tonal Plexus, and named by them a "mem". It gives a negligible error for its mapping of prime-factor 5 at + 0.47%, and also low error for prime-factor 3 as well as several higher primes, thus it is a good approximation of 5-limit JI. It can function as 5 bike-chains of 41-edo.
205edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 205 0 0
5 476 +0.03 +0.47
37 1068 +0.36 +6
17 838 +0.41 +7
3 325 +0.48 +8
29 996 +0.67 +11
19 871 +1.02 +17
11 709 -1.07 -18
41 1098 -1.75 -30
23 927 -1.93 -33
43 1112 -2.25 -38
31 1016 +2.28 +39
13 759 +2.40 +41
7 576 +2.88 +49
|

|
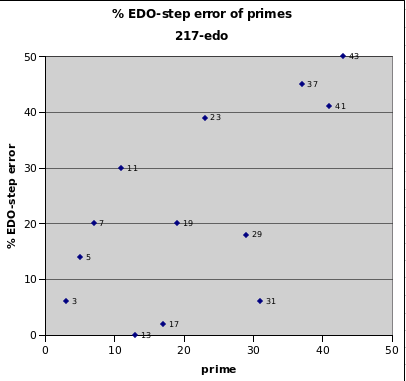
217edo
217edo is another cardinality which gives a negligible error for a 43-limit prime-factor: the error of its mapping of 13 is +0.5%. Other excellent representations are those for 3, 17, and 31, with fairly good representations of 5 and 7. Its main interest is that it can work as an adaptive-JI in the form of 7 bike-chains of 31edo, two of which are nearly identical to Vicentino's adaptive-JI of 1555. Use of this tuning for the common-practice repertoire would allow much of it to be performed in adaptive-JI.
217edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 217 0 0
13 803 +0.03 +0.5
17 887 +0.11 +2
31 1075 -0.34 -6
3 344 +0.35 +6
5 504 +0.78 +14
29 1054 -1.01 -18
7 609 -1.08 -20
19 922 +1.10 +20
11 751 +1.68 +30
23 982 +2.14 +39
41 1163 +2.27 +41
37 1130 -2.50 -45
43 1177 -2.76 -50
|
|
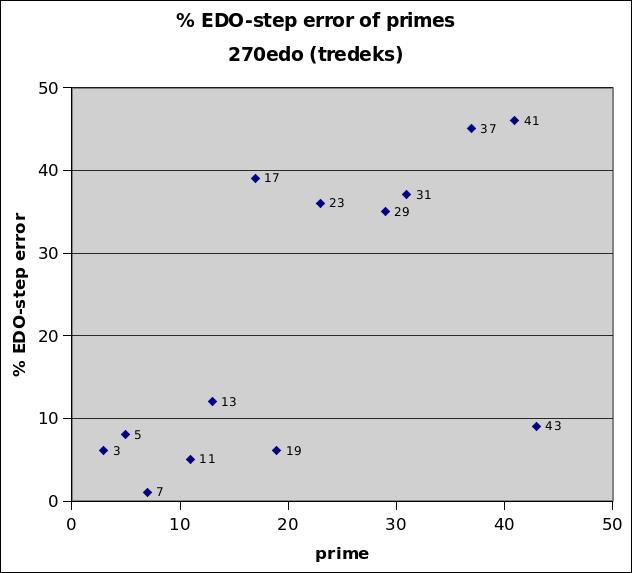
270edo
270edo is very useful as an integer unit of interval measurement up to the 13-prime-limit. Since 270 is a fairly high cardinality, the absolute error amounts are all fairly small. What is important is that all prime-factors up to the 13-limit are approximated with extremely small relative error (i.e., percentage of a 270-edo degree), all less than 13%, which thus obviates the need for decimal places when mapping 13-limit JI to 270edo. Joseph Monzo advocates its use for this, with the name "tredek", as a replacement for cents. (One possible disadvantage is that the 12-edo semitone maps exactly between two tredeks; this can be remedied by instead using the dexl as a unit of measurement.)
270edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 270 0 0
7 758 +0.06 +1
11 934 -0.21 +5
19 1147 +0.26 +6
3 428 +0.27 +6
5 617 +0.35 +8
43 1465 -0.41 -9
13 999 -0.53 -12
29 1312 +1.53 +35
23 1221 -1.61 -36
31 1338 +1.63 +37
17 1104 +1.71 +39
37 1407 +1.99 +45
41 1447 +2.05 +46
|
|
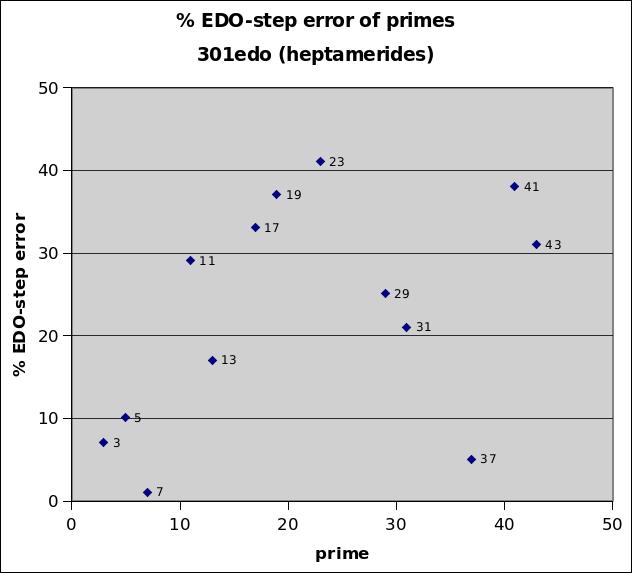
301edo
301edo is the first 3 digits of accuracy of the base-10 logarithm of 2, which in previous centuries could be looked up in printed tables and thus obviated the need for performing further calculations. It has extremely low error for its mapping of prime-factor 7, and also good representations of 3 and 5 -- thus is works well as an integer unit of measurement for 7-limit JI, and was named heptaméride by Sauveur. It also functions as 7 bike-chains of 43edo, which is very close to 1/5-comma meantone. In fact, several of the temperings of 43edo from the related just intervals are measureable in nearly exact heptamérides.
301edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 301 0 0
7 845 -0.06 -1
37 1568 -0.18 -5
3 477 -0.29 -7
5 699 +0.40 +10
13 1114 +0.67 +17
31 1491 -0.85 -21
29 1462 -1.01 -25
11 1041 -1.15 -29
43 1633 -1.22 -31
17 1230 -1.30 -33
19 1279 +1.49 +37
41 1613 +1.50 +38
23 1362 +1.63 +41
|
|
311edo
311edo is very useful as an integer unit of interval measurement all the way up to the 41-prime-limit. Since 311 is a fairly high cardinality, the absolute error amounts are all fairly small. What is important is that all prime-factors up to the 41-limit are approximated with very little relative error (i.e., percentage of a 311 degree), with all errors evenly distributed between 8% and 24%, which thus obviates the need for decimal places when mapping 41-limit JI to 311edo. Joseph Monzo advocates its use for this, with the name "gene", as a replacement for cents.
311edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 311 0 0
3 493 +0.30 +8
7 873 -0.34 -9
19 1321 -0.41 -11
11 1076 +0.45 +12
5 722 -0.46 -12
37 1620 -0.54 -14
13 1151 +0.63 +16
29 1511 +0.65 +17
23 1407 +0.66 +17
41 1666 -0.77 -20
17 1271 -0.78 -20
31 1541 +0.95 +24
43 1688 +1.67 +43
|

|
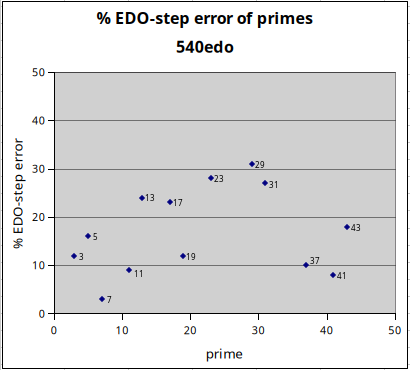
540edo
540edo is useful as an integer unit of interval measurement for the 43-prime-limit. Since 540 is a fairly high cardinality, the absolute error amounts in 43-limit are all ~1 cent or less. All prime-factors up to the 43-limit are approximated with less than 31% relative error (i.e., percentage of a 540-edo degree) obviating the need for decimal places when mapping 43-limit JI to 540edo. Its approximations to primes 2, 3, 5, 7, 11, 13, and 19 are exactly the same size as those of 270edo, and those of all other primes in the 43-limit are better. In addition, 540edo divides exactly into 12 (45\540), thus enabling easy comparison with 12edo in a manner similar to cents. Joseph Monzo advocates its use for this, with the name "dexl" (derived from its Roman numeral DXL), as a replacement for cents.
540edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 540 0 0
7 1516 +0.1 3
41 2893 -0.2 8
11 1868 -0.2 9
37 2813 -0.2 10
3 856 +0.3 12
19 2294 +0.3 12
5 1254 +0.4 16
43 2930 -0.4 18
17 2207 -0.5 23
13 1998 -0.5 24
31 2675 -0.6 27
23 2443 +0.6 28
29 2623 -0.7 31
|
|
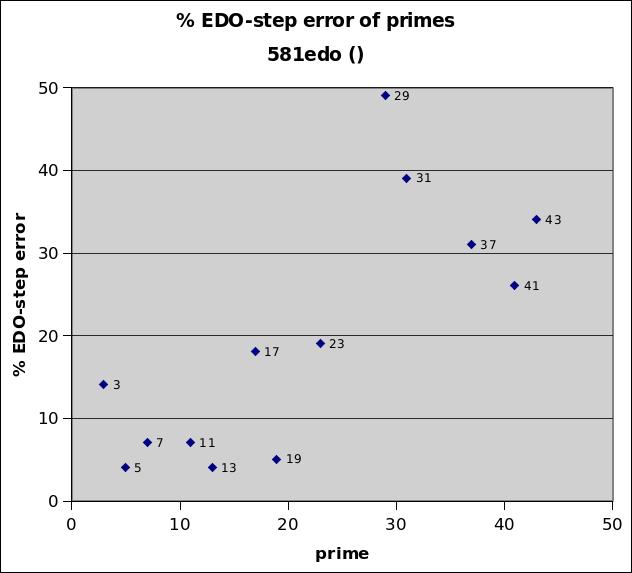
581edo
581edo is very useful as an integer unit of interval measurement up to the 23-prime-limit. Since 581 is a fairly high cardinality, the absolute error amounts in 43-limit are all ~1 cent or less. What is important is that all prime-factors up to the 23-limit are approximated with very small relative error (i.e., percentage of a 581-edo degree), all less than 20%, with the relative error for primes 5, 7, 11, 13, and 19 all under 8%, and the relative error for primes 3, 17, and 23 between 10% and 20%, which thus obviates the need for decimal places when mapping 23-limit JI to 581edo. Joseph Monzo advocates its use for this, with the name "spook", as a replacement for cents.
581edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 581 0 0
5 1349 -0.08 -4
13 2150 +0.09 +4
19 2468 -0.09 -5
11 2010 +0.15 +7
7 1631 -0.15 -7
3 921 +0.28 +14
17 2375 +0.38 +18
23 2628 -0.39 -19
41 3113 +0.54 +26
37 3027 +0.64 +31
43 3153 +0.70 +34
31 2878 -0.80 -39
29 2822 -1.01 -49
|
|
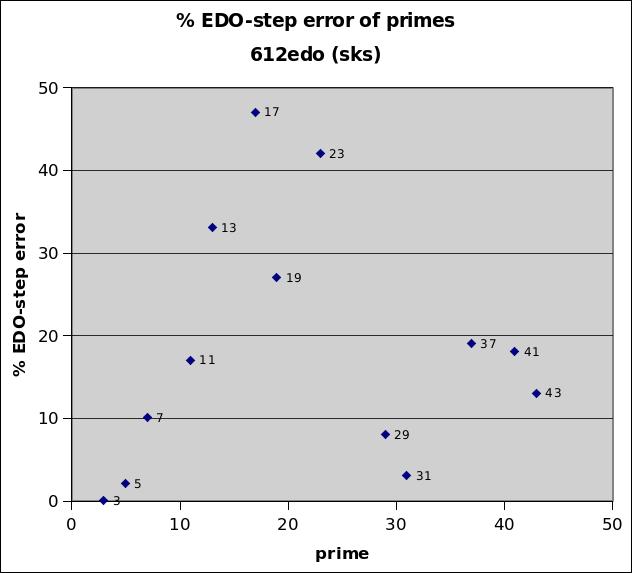
612edo
612edo has negligible relative error for its mapping of prime-factor 3, at +0.29%. It is useful as an accurate integer measurement of 5-limit JI.
612edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 612 0 0
3 970 +0.01 +0.29
5 1421 -0.04 -2
31 3032 +0.06 +3
29 2973 -0.17 -8
7 1718 -0.20 -10
43 3321 +0.25 +13
11 2117 -0.34 -17
41 3279 +0.35 +18
37 3188 -0.36 -19
19 2600 +0.53 +27
13 2265 +0.65 +33
23 2768 -0.82 -42
17 2502 +0.93 +47
|
|
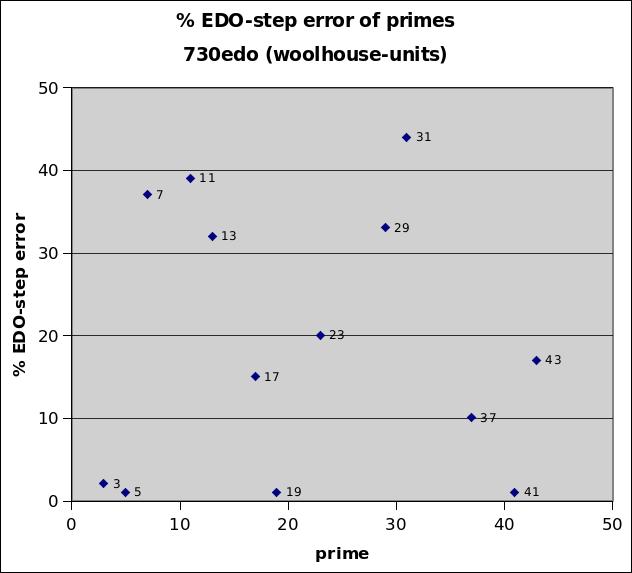
730edo
730edo was introduced in 1835 by Wesley Woolhouse as a very accurate integer measurement of the basic intervals in 5-limit JI.
730edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 730 0 0
5 1695 -0.01 -0.75
19 3101 +0.0212 +1.29
41 3911 -0.0213 -1.3
3 1157 -0.04 -2.26
37 3803 +0.16 +10
17 2984 +0.25 +15
43 3961 -0.28 -17
23 3302 -0.33 -20
13 2701 -0.53 -32
29 3546 -0.54 -33
7 2049 -0.61 -37
11 2525 -0.63 -39
31 3617 +0.72 +44
|
|
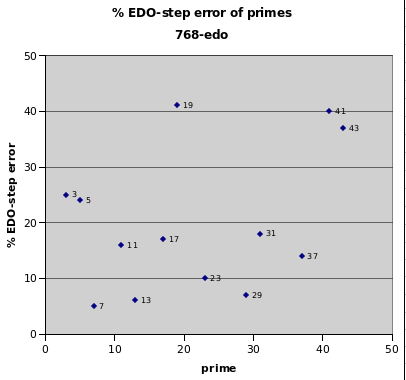
768edo
768edo is important for users of MIDI, because it is a standard tuning resolution on many MIDI instruments and soundcards. One degree of 768edo is a hexamu.
At this level of resolution, even the largest error shown is still less than 2/3 cent. But it is important to know how 768edo maps the primes because a MIDI user may get different results than expected because of rounding errors or data truncation.
768edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 768 0 0
7 2156 -0.08 -5
13 2842 +0.10 +6
29 3731 +0.11 +7
23 3474 -0.15 -10
37 4001 +0.22 +14
11 2657 +0.24 +16
17 3139 -0.27 -17
31 3805 +0.28 +18
5 1783 -0.38 -24
3 1217 -0.39 -25
43 4167 -0.58 -37
41 4115 +0.63 +40
19 3262 -0.64 -41
|
|
1000edo
1000edo is important because of its use by some tuning theorists as a unit of logarithmic interval measurement, known as the millioctave. It is a division of the octave into exactly 1000 equal parts. Besides its ease of decimal calculation, one main reason for its employment is to avoid referring intervals to the familiar 12-edo tuning.
1000edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 1000 0 0
29 4858 +0.023 +2
3 1585 +0.045 +4
5 2322 +0.086 +7
19 4248 +0.087 +7
31 4954 -0.236 -20
43 5426 -0.318 -26
7 2807 -0.426 -35
11 3459 -0.518 -43
23 4524 +0.526 +44
13 3700 -0.528 -44
41 5358 +0.538 +45
37 5209 -0.544 -45
17 4087 -0.555 -46
|

|
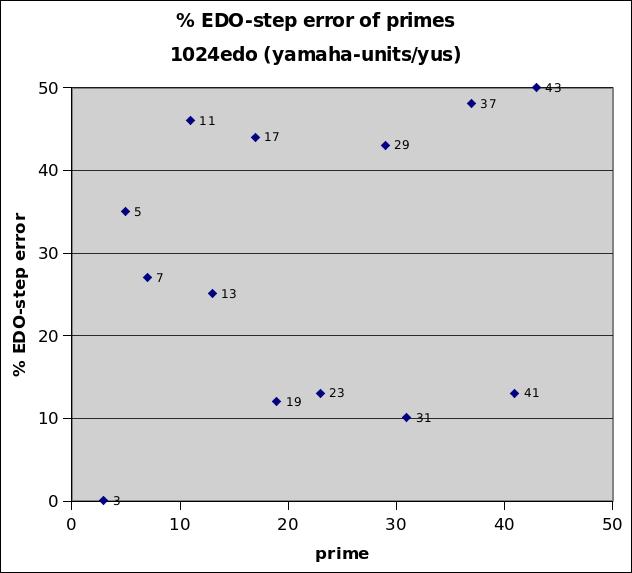
1024edo
1024edo is important as the tuning resolution that was incorporated into a wide variety of electronic instruments manufactured by Yamaha in the 1980s and 1990s, which were some of the earliest relatively inexpensive electronic instruments capable of microtonality. It was named yu (for "Yamaha unit") by Joseph Monzo. It was chosen as an easily computible division, since the octave is divided into 2^10 (= 1024) equal parts. It happens to have negligible error in its mapping of prime-factor 3, with only -0.16% relative error -- thus, it is both an outstanding logarithmic measurement for pythagorean tuning, and capable of rendering pythogorean tuning on the Yamaha instruments with extreme accuracy.
1024edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 1024 0 0
3 1623 -0.002 -0.16
31 5073 -0.11 -10
19 4350 +0.14 +12
23 4632 -0.15 -13
41 5486 -0.16 -13
13 3789 -0.29 -25
7 2875 +0.31 +27
5 2378 +0.41 +35
29 4975 +0.50 +43
17 4186 +0.51 +44
11 3542 -0.54 -46
37 5334 -0.56 -48
43 5556 -0.58 -50
|
|
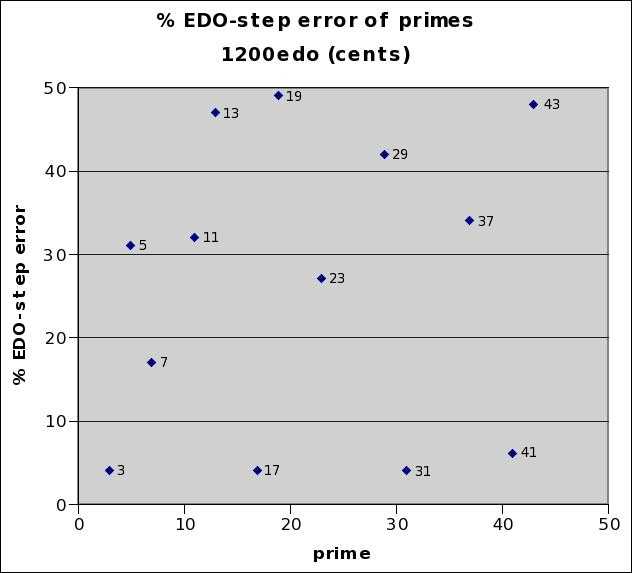
1200edo
1200edo is important because of its widespread use as a unit of logarithmic interval measurement, known as the cent. It is a division of the 12-edo semitone into exactly 100 equal parts.
On all the equal-temperaments presented on this page, the error is given as both an absolute value, in cents, and as a relative value, in the percentage of one step of that equal-temperament. Because 1200-edo defines the cent, both sets of values here are equivalent. This analysis shows it as a mapping, as with all the other EDOs on this page, but in general usage, cents are normally used as an integer measurement only informally in actual musical performance; otherwise they are treated as a floating-point value.
1200edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 1200 0 0
31 5945 -0.036 -3.6
17 4905 +0.0446 +4.46
3 1902 +0.045 +4.5
41 6429 -0.06 -6
7 3369 +0.17 +17
23 5428 -0.27 -27
5 2786 -0.31 -31
11 4151 -0.32 -32
37 6251 -0.34 -34
29 5830 +0.42 +42
13 4441 +0.47 +47
43 6512 +0.48 +48
19 5098 +0.49 +49
|
|
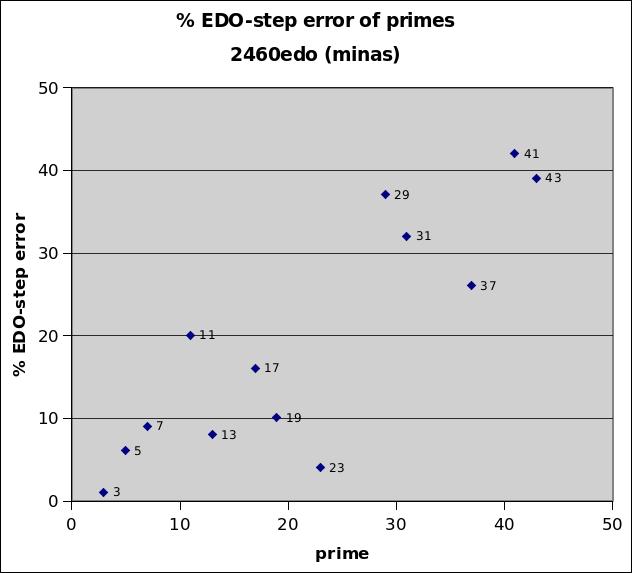
2460edo
2460edo is a unit of integer logarithmic interval measurement called the mina, named by Gene Ward Smith, and used by George Secor and Dave Keenan in their invention of sagittal notation. Its mappings to prime-factors 3, 5, 7, 13, 19, and 23 all have relative error under 10%, and those of primes 11 and 17 between 15% and 20%. Thus it is an excellent integer measurement for 7-limit JI, and fairly good for 23-limit JI. It is exactly divisible into, and thus contains, all of the following EDOs within it: 5, 6, 10, 12, 15, 20, 30, 41, 60, 82, 123, 164, 205, 246, 410, 492, 615, 820, and 1230, and therefore may be used as bike-chains of all of these tunings.
2460edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 2460 0 0
3 3899 -0.00 -0.8
23 11128 +0.02 +4
5 5712 +0.03 +6
13 9103 -0.04 -8
7 6906 -0.05 -9
19 10450 +0.05 +9.8
17 10055 -0.08 -16
11 8510 -0.10 -20
37 12815 -0.12 -26
31 12187 -0.16 -32
29 11951 +0.18 +37
43 13349 +0.19 +39
41 13180 +0.21 +42
|
|
6691edo
6691edo is useful as a unit of integer logarithmic interval measurement for 11-limit JI, and is especially good for 7-limit JI. It has outstanding representations of prime-factors 3, 5, and 7, and a very good mapping of 11. Its approximations of 19, 23, and 43 are fairly good, of 17 and 29 mediocre, and of 13, 37, 41, and 43 poor.
6691edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 6691 0 0
7 18784 -0.0021 -1.2
3 10605 +0.0029 +1.59
5 15536 -0.0037 -2.09
11 23147 -0.0102 -5.7
19 28423 +0.0210 +12
43 36307 -0.0247 -14
23 30267 -0.0274 -15
17 27349 -0.0384 -21
29 32505 +0.0447 +25
13 24760 +0.0642 +36
41 35847 -0.0682 -38
37 34856 -0.0811 -45
31 33149 +0.0847 +47
|

|
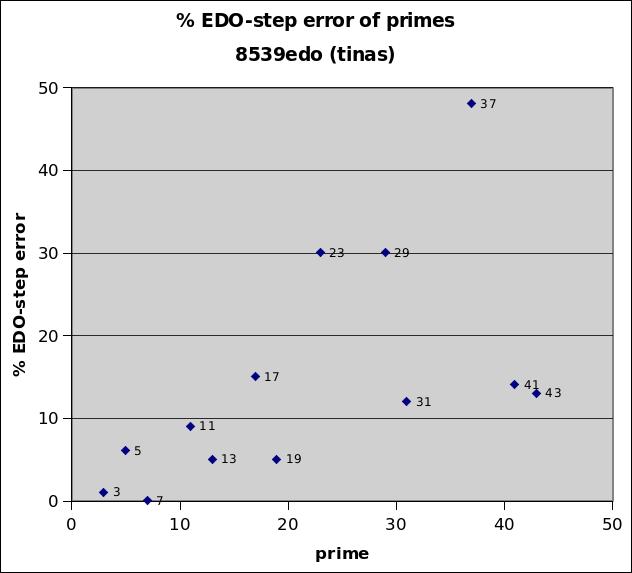
8539edo
8539edo is advocated by Joseph Monzo as a integer logarithmic interval measurement to replace cents, the tina. Described first by George Secor then Gene Ward Smith, it was discovered by Monzo independently using a weighted error analysis, where prime-factor 3 was given by far the greatest weight, with the weights decreasing thru 5, 7, and 11, with primes 13 to 43 left unweighted. It gives excellent representations thru the 13-limit and also for prime-factor 19, fairly good representations for 17, 31, 41, and 43, mediocre for 23 and 29, and in the 43-limit only 37 having a poor representation.
8539edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 8539 0 0
7 23972 -0.0005 -0
3 13534 +0.0007 +1
19 36273 -0.0075 -5
13 31598 -0.0077 -5
5 19827 +0.0079 +6
11 29540 -0.012 -9
31 42304 +0.017 +12
43 46335 +0.018 +13
41 45748 -0.019 -14
17 34903 +0.022 +15
29 41482 -0.042 -30
23 38627 +0.043 +30
37 44484 +0.067 +48
|
|
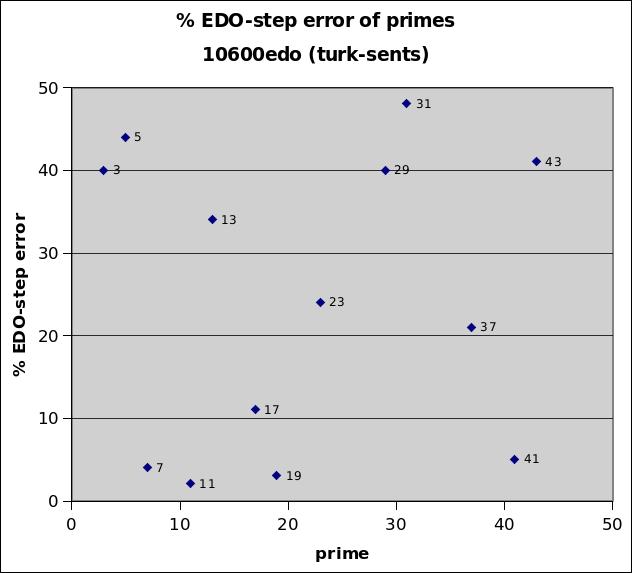
10600edo
10600edo is an integer logarithmic interval measurement which divides each degree of 53edo (long accepted as the basis of Turkish music) into 200 parts. Known as the t¨rk-sent, it was advocated for use in measuring the microtonal inflections of traditional Turkish music.
10600edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 10600 0 0
11 36670 +0.003 2
19 45028 -0.004 3
7 29758 +0.004 4
41 56790 -0.006 5
17 43327 -0.012 11
37 55220 -0.023 21
23 47950 +0.028 24
13 39225 +0.038 34
3 16801 +0.045 40
29 51495 +0.0454 40
43 57518 -0.046 41
5 24612 -0.050 44
31 52514 -0.054 48
|
|
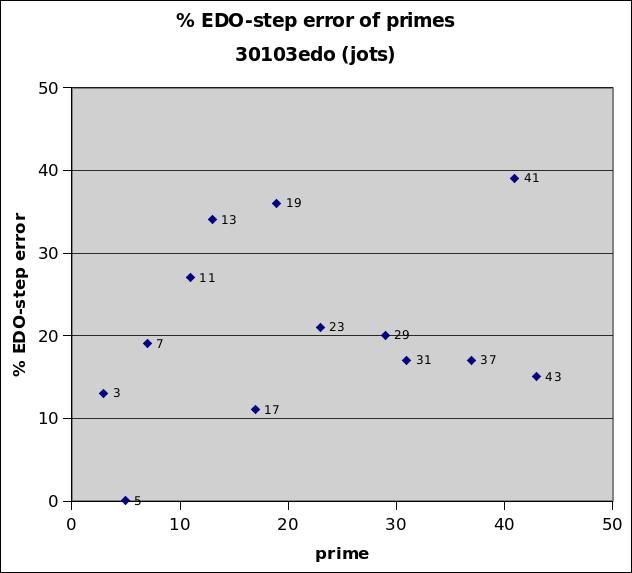
30103edo
30103edo is a logarithmic interval measurement known as the jot. It was employed because to 5 digits of accuracy the log_10 of 2 (the octave) is ~0.30103 (to more digits of accuracy, ~0.30102999566398114), the idea being that if tables of base-2 logarithms were available, one need only look up the corresponding log_2 of an interval and then multiply by 100,000, which can easily be done mentally by simply ignoring the decimal point and the zero before it. 30103edo represents prime-factor 5 with essentially no error (~1/694 of a degree), gives good approximations of primes 17, 3, 43, 31, 37, 7, 29, and 23, a mediocre approximation of 11, and poor approximations of primes 13, 19, and 41.
30103edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 30103 0 0
5 69897 -0.00006 -0.144
17 123045 +0.004 +11
3 47712 -0.005 -13
43 163347 +0.006 +15
31 149136 -0.0068 -17
37 156820 -0.007 -17
7 84510 +0.008 +19
29 146240 +0.008 +20
23 136173 +0.009 +21
11 104139 -0.011 -27
13 111394 -0.013 -34
19 127875 -0.014 -36
41 161278 -0.015 -39
|
|
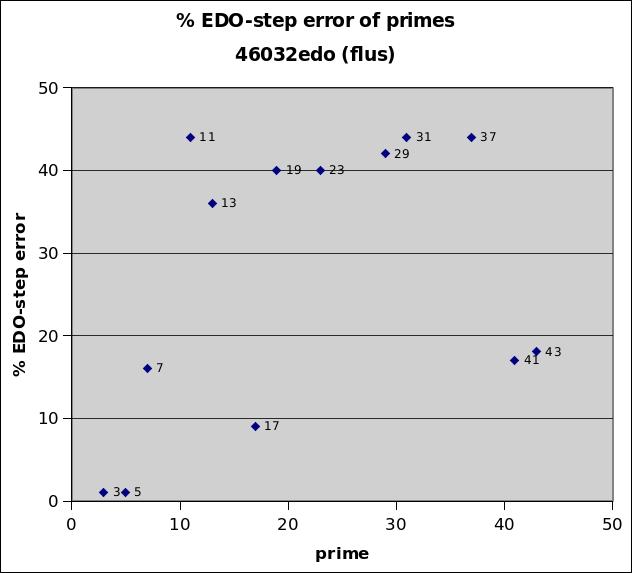
46032edo
46032edo is an integer logarithmic interval measurement advocated by Gene Ward Smith, and named by him the flu.
46032edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 46032 0 0
3 72959 +0.00016 +1
5 106883 +0.00015 +1
7 129228 -0.0042 -16
11 159245 +0.0116 +44
13 170339 +0.0094 +36
17 188154 -0.0023 -9
19 195541 +0.0104 +40
23 208229 +0.0103 +40
29 223623 +0.0109 +42
31 228052 +0.0114 +44
37 239802 +0.0115 +44
41 246619 +0.0043 +17
43 249782 +0.0047 +18
|
|
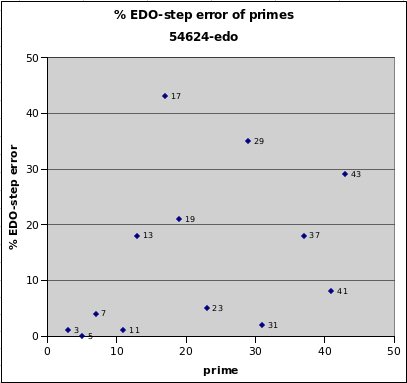
54624edo
54624edo is a superb integer logarithmic interval measurement for 11-limit JI, to replace cents. Its representations of 3, 5, 7, 11, and 31 are outstanding, those of 23 and 41 extremely good, of 13, 19, and 37 fair, and of 17, 29, and 43 poor.
54624edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 54624 0 0
5 126833 -0.00001 -0.03
11 188968 +0.00016 +0.73
3 86577 +0.00018 +0.84
31 270618 -0.0004 -2
7 153349 +0.001 +4
23 247095 -0.0011 -5
41 292651 +0.0017 +8
13 202133 +0.004 +18
37 284561 -0.004 -18
19 232039 +0.0046 +21
43 296404 -0.0063 -29
29 265362 -0.0078 -35
17 223274 +0.0094 +43
|
|
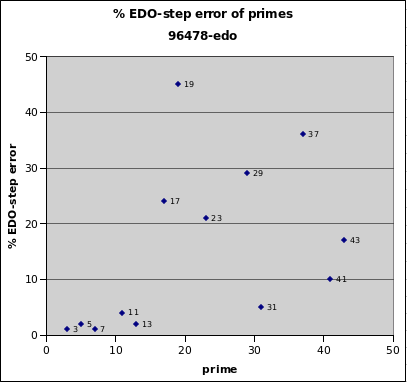
96478edo
96478edo is a superb integer logarithmic interval measurement for 13-limit JI, to replace cents. Its representations of 3, 5, 7, 11, 13, and 31 are outstanding, that of 41 quite good, of 17, 23, and 43 mediocre, and of 19, 29, and 37 poor.
96478edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 96478 0 0
3 152914 -0.00015 -1
7 270848 +0.00015 +1
5 224015 +0.00026 +2
13 357011 -0.00029 -2
11 333759 -0.00054 -4
31 477971 +0.0006 +5
41 516886 +0.00122 +10
43 523515 -0.00213 -17
23 436424 -0.0026 -21
17 394350 -0.003 -24
29 468688 -0.00361 -29
37 502598 +0.00446 +36
19 409832 +0.0056 +45
|
|
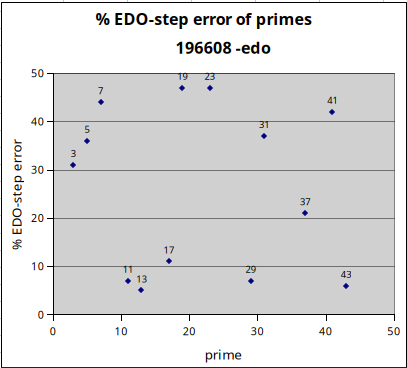
196608edo
196608edo is important because it is the greatest tuning resolution available in the MIDI Tuning Standard (MTS). Joseph Monzo gave one degree of this tuning the name tetradekamu (14mu). The range for MIDI pitch-bend is variable, and the minimum range the user may specify is one 12edo semitone. With the maximum pitch-bend resolution of 14 bits, each semitone is divided into 2^14 = 16384 parts, thus resulting in an EDO with (2^14 * 12) = 196608 degrees to the octave. Its representations of 13, 43, 11, 29, and 17 are excellent, that of 37 fairly mediocre, and those of 3, 5, 31, 41, 7, 19, and 23 quite poor.
196608edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 96478 0 0
13 738637 -0.0003 -5
43 1066847 -0.0004 -6
11 690530 +0.0004 +6.8
29 969692 +0.0004 +7.3
17 815890 +0.0006 +11
37 1039849 -0.0013 -21
3 316371 -0.0019 -31
5 463475 +0.0022 +36
31 988897 +0.0023 +37
41 1069410 +0.0025 +42
7 560371 -0.0027 -44
19 847920 +0.0029 +46.7
23 902939 -0.0029 +46.9
|
|
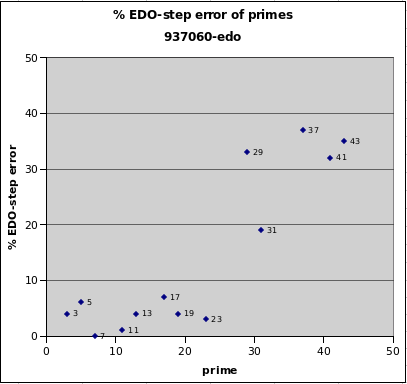
937060edo
937060edo is an outstanding integer logarithmic interval measurement for 23-limit JI, to replace cents. Its representations of 3, 5, 7, 11, 13, 17, 19 , and 23 are all under 7% error, its representation of 31 is mediocre, and those of 29, 37, 41 and 43 quite poor.
937060edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 937060 0 0
7 2630660 -0.000004 -0.33
11 3241695 +0.00001 +0.74
23 4238849 +0.00004 +3.35
3 1485205 +0.00005 +3.91
13 3467534 -0.00005 -4.23
19 3980563 +0.00006 +4.43
5 2175786 +0.00008 +6
17 3830198 +0.00009 +7
31 4642379 -0.00025 -19
29 4552220 +0.00042 +33
37 4881570 -0.00047 -37
41 5020348 +0.00041 +32
43 5084736 +0.00045 +35
|
|
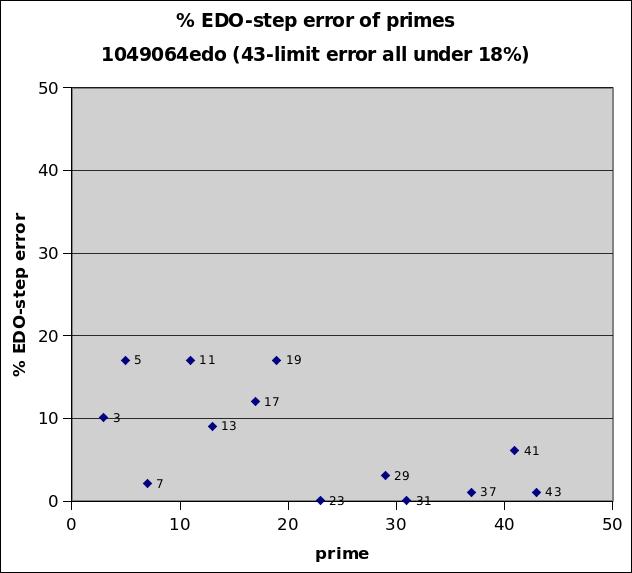
1049064edo
1049064edo is an excellent integer logarithmic interval measurement for 43-limit JI, to replace cents. Its representations of all 43-limit prime-factors have less than 18% error.
1049064edo best representation of prime-factor
prime edo ~cents % EDO-step
degrees error error
2 1049064 0 0
23 4745506 +0.0000001 0
31 5197269 +0.000002 0
43 5692499 +0.00001 1
37 5465050 +0.000017 1
7 2945095 +0.000018 2
29 5096333 +0.00003 3
41 5620415 +0.00007 6
13 3881998 -0.000106 9
3 1662727 -0.000115 10
17 4288010 -0.000135 12
5 2435851 -0.0002 17
11 3629165 -0.0001963 17
19 4456348 +0.0001956 17
|
|
Comparison of different EDO prime-error graphs
©2003 by Joseph Monzo
Comparison of different EDO prime-error graphs
©2003 by Joseph Monzo
MouseOver the cardinality names of the various
Please make a donation to help keep Tonalsoft online. A recurring monthly contribution would be apprecitated.
Thank you!

