dexl / 540-edo

A small unit of interval measurement, suggested by Joseph Monzo in April 2023.

A dexl divides the octave into 540 equal parts. Its name was coined by Monzo from the Roman numeral for 540, which is DXL. Its use is valuable because it has very low relative error for the just-intonation ratio mappings for the prime-factors thru the 43-prime-limit, thus obviating the need for decimal places in measuring those intervals logarithmically.

The dexl is therefore calculated as the 540th root of 2, or 2^{^(1/540)}, with a ratio of approximately 1:1.001284430064567. It is an irrational number.

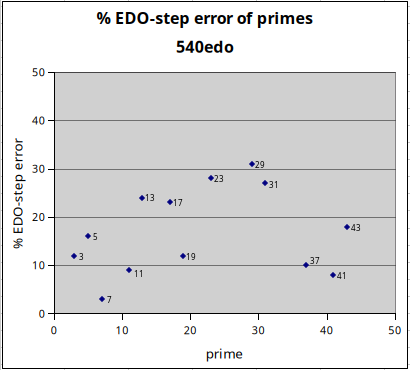
540edo is useful as an integer unit of interval measurement for the 43-prime-limit. Since 540 is a fairly high cardinality, and its approximations are so good, the amounts of absolute error in 43-limit are all less than ³/₄ cent. The relative error (i.e., percentage of a 540-edo degree) of the best mapping of all prime-factors up to the 43-limit is less than 31%. Its approximations to primes 2, 3, 5, 7, 11, 13, and 19 are exactly the same size as those of 270edo (the numbers of the mappings being double those of the tredeks), and those of all other primes in the 43-limit are better, some significantly so. Another valuable feature is that 540edo divides exactly into 12, making the 12edo semitone exactly 45\540, thus enabling easy comparison with 12edo in a manner similar to cents. For these reasons, Joseph Monzo advocates its use as a replacement for cents.

540edo best representation of prime-factor prime edo ~cents % EDO-step degrees error error 2 540 0 0 7 1516 +0.1 3 41 2893 -0.2 8 11 1868 -0.2 9 37 2813 -0.2 10 3 856 +0.3 12 19 2294 +0.3 12 5 1254 +0.4 16 43 2930 -0.4 18 17 2207 -0.5 23 13 1998 -0.5 24 31 2675 -0.6 27 23 2443 +0.6 28 29 2623 -0.7 31

A dexl is:

• exactly ¹/₄₅ (= 0.0,2... ) semitone.
• exactly ²/₄₅ (= 0.0,4... = ~ ¹/₂₂ ) quarter-tone.
• exactly ³¹/₅₄₀ (= 0.05,740... = ~ ¹/₁₇ ) diesis.
• exactly ⁴³/₅₄₀ (= 0.07,962... = ~ ¹/₁₂ ) méride.
• exactly ²/₁₅ (= 0.1,3... = ~ ¹/₈ ) morion.
• exactly ¹/₂ (= 0.5 ) tredek.
• exactly 1 + ¹⁹/₄₅ (= 1.4,2... = ~ 1 + ²/₅ ) 6mus.
• exactly 1 + ²³/₂₇ (= 1.851... = ~ 1 + ⁵/₆ ) millioctaves.
• exactly 1 + ¹²¹/₁₃₅ (= 1.8,962... = ~ 1 + ⁹/₁₀ ) yamaha-units.
• exactly 2 + ²/₉ (= ~2.2... = ~ 2 + ¹/₅ ) cents.
• exactly 4 + ⁵/₉ (= 4.5... = ~ 4 + ¹/₂) minas.
• exactly 15 + ⁴³⁹/₅₄₀ (= 15.81,296... = ~ 15 +⁵/₆ ) tinas.
• exactly 19 + ¹⁷/₂₇ (= 19.629... = ~ 19 + ²/₃ ) türk-sents.
• exactly 91 + ¹/₄₅ (= 91.0,2... = ~ 91 ) 12mus.
• exactly 364 + ⁴/₄₅ (= 364.0,8... = ~ 364 + ¹/₁₁ ) 14mus.

The formula for calculating the floating-point dexl-value of any ratio r is: dexls = log_{_10}(r) * [ 540 / log_{_10}(2) ] or dexls = log_{_2}(r) * 540

However, the primary benefit in using dexls as a logarithmic interval measurement for 43-limit JI is that there is hardly any significance to any of the values after the decimal point, so that one may memorize the integer dexl values of 43-limit ratio mappings and compute with them, with little concern for rounding errors.

A dexl represents one degree of 540-edo tuning.

The 12-edo semitone is exactly 45 dexls, making the 12-edo 5th = exactly 315 dexls. This is the second-best mapping of prime-factor 3 in 540-edo, so in terms of a chain-of-5ths tuning, this also represents the wart 540b. Below is a table of 12-edo measured in dexls:

 12-edo   540-edo (dexls)
		
    12    540    A       
    11    495    G# Ab   
    10    450    G       
     9    405    F# Gb   
     8    360    E# F    
     7    315    E  Fb
     6    270    D# Eb
     5    225    D
     4    180    C# Db
     3    135    B# C
     2     90    B  Cb
     1     45    A# Bb
     0      0    A
		

540-edo provides very good approximations or exact matches to the 5th of several important tunings, among them:

			11\18 and 22\36 = 330 dexls (exactly)
			3\5 and 9\15 = 324 dexls (exactly)
			22\37 ~= 321 dexls
			16\27 = 320 dexls (exactly)
			13\22 ~= 319 dexls
			27\46 ~= 317 dexls
			24\41 ~= 316 dexls
			 7\12, 14\24, 21\36, 28\48, 42\72, 84\144, etc. = 315 dexls (exactly)
			25\43 and 1/5-comma meantone ~= 314 dexls  xxxxxxxxxxxx
			29\50, 2/7-comma meantone, and Lucy tuning ~= 313 dexls.
			

some intervals mapped to 540-edo

			
====================================
edomap.py (c)2008-12-23 by Joe Monzo
====================================

Finds the EDO mappings for a set of ratios

=============== new run =====================

please enter edo: 540

any displaced mappings? ... 0=no, 1=yes : 0


540 -edo floating-point mappings:

prime edo-steps   step-error  edo-map

 2 =  540.000000    +0.00 -->    540  (same as 270edo)
 3 =  855.879750    +0.12 -->    856  (same as 270edo)
 5 = 1253.841171    +0.16 -->   1254  (same as 270edo)
 7 = 1515.971658    +0.03 -->   1516  (same as 270edo)
11 = 1868.093074    -0.09 -->   1868  (same as 270edo)
13 = 1998.237448    -0.24 -->   1998  (same as 270edo)
17 = 2207.229934    -0.23 -->   2207
19 = 2293.880857    +0.12 -->   2294  (same as 270edo)
23 = 2442.723456    +0.28 -->   2443
29 = 2623.309737    -0.31 -->   2623
31 = 2675.266008    -0.27 -->   2675
37 = 2813.104817    -0.10 -->   2813
41 = 2893.078082    -0.08 -->   2893

integer (i.e., true) mappings, compared with cents-value of actual prime

map  2 -->    540 = 1200.000000 cents <-- 1200.000000  +0.0 cents
map  3 -->    856 = 1902.222222 cents <-- 1901.955001  +0.3 cents
map  5 -->   1254 = 2786.666667 cents <-- 2786.313714  +0.4 cents
map  7 -->   1516 = 3368.888889 cents <-- 3368.825906  +0.1 cents
map 11 -->   1868 = 4151.111111 cents <-- 4151.317942  -0.2 cents
map 13 -->   1998 = 4440.000000 cents <-- 4440.527662  -0.5 cents
map 17 -->   2207 = 4904.444444 cents <-- 4904.955410  -0.5 cents
map 19 -->   2294 = 5097.777778 cents <-- 5097.513016  +0.3 cents
map 23 -->   2443 = 5428.888889 cents <-- 5428.274347  +0.6 cents
map 29 -->   2623 = 5828.888889 cents <-- 5829.577194  -0.7 cents
map 31 -->   2675 = 5944.444444 cents <-- 5945.035572  -0.6 cents
map 37 -->   2813 = 6251.111111 cents <-- 6251.344039  -0.2 cents
map 41 -->   2893 = 6428.888889 cents <-- 6429.062406  -0.2 cents

--------------

examples:

              ratio      -->     540 -edo mapping:

       ratio           cents    error        edo      cents     name

        2:1         =  1200.0   +0.0 -->   540 \ 540  = 1200.0  (octave)
    65536:32805     =  1198.0   -2.5 -->   538 \ 540  = 1195.6  (minimal just dim-2)
     2025:1024      =  1180.4   +1.8 -->   532 \ 540  = 1182.2  (small just aug-7th)
  1048576:531441    =  1176.5   -3.2 -->   528 \ 540  = 1173.3  (pythagorean dim-2nd)
      125:64        =  1158.9   +1.1 -->   522 \ 540  = 1160.0  (minimal just aug-7th)
       31:16        =  1145.0   -0.6 -->   515 \ 540  = 1144.4  (31st harmonic)
       48:25        =  1129.3   -0.4 -->   508 \ 540  = 1128.9  (small just dim-8ve)
       21:11        =  1119.5   +0.5 -->   504 \ 540  = 1120.0  (undecimal diminished-8ve)
      243:128       =  1109.8   +1.3 -->   500 \ 540  = 1111.1  (pythagorean major-7th)
      256:135       =  1107.8   -1.2 -->   498 \ 540  = 1106.7  (minimal just dim-8ve)
       15:8         =  1088.3   +0.6 -->   490 \ 540  = 1088.9  (15th harmonic, large just major-7th, 5*3)
     4096:2187      =  1086.3   -1.9 -->   488 \ 540  = 1084.4  (pythagorean diminished-8ve)
       13:7         =  1071.7   -0.6 -->   482 \ 540  = 1071.1  (tridecimal superminor-7th)
       50:27        =  1066.8   -0.1 -->   480 \ 540  = 1066.7  (small just maj-7th)
       24:13        =  1061.4   +0.8 -->   478 \ 540  = 1062.2  (tridecimal major-7th)
       11:6         =  1049.4   -0.5 -->   472 \ 540  = 1048.9  (undecimal submajor[neutral]-7th)
       20:11        =  1035.0   +0.6 -->   466 \ 540  = 1035.6  (undecimal superminor[neutral]-7th)
       29:16        =  1029.6   -0.7 -->   463 \ 540  = 1028.9  (29th harmonic)
    59049:32768     =  1019.6   +2.7 -->   460 \ 540  = 1022.2  (pythagorean aug-6th)
        9:5         =  1017.6   +0.2 -->   458 \ 540  = 1017.8  (just minor-7th)
     3645:2048      =   998.0   +2.0 -->   450 \ 540  = 1000.0  (large just aug-6th)
       16:9         =   996.1   -0.5 -->   448 \ 540  =  995.6  (pythagorean minor-7th)
      225:128       =   976.5   +1.2 -->   440 \ 540  =  977.8  (small just augmented-6th)
        7:4         =   968.8   +0.1 -->   436 \ 540  =  968.9  (7th harmonic, septimal subminor-7th)
      216:125       =   946.9   -0.3 -->   426 \ 540  =  946.7  (large just dim-7)
       19:11        =   946.2   +0.5 -->   426 \ 540  =  946.7  (nondecimal supermajor-6th)
       12:7         =   933.1   +0.2 -->   420 \ 540  =  933.3  (septimal supermajor-6th)
      128:75        =   925.4   -1.0 -->   416 \ 540  =  924.4  (small just dim-7th)
       22:13        =   910.8   +0.3 -->   410 \ 540  =  911.1  (tridecimal augmented-6th)
       27:16        =   905.9   +0.8 -->   408 \ 540  =  906.7  (27th harmonic, pythagorean major-6th)
     2048:1215      =   903.9   -1.7 -->   406 \ 540  =  902.2  (minimal just dim-7)
        5:3         =   884.4   +0.1 -->   398 \ 540  =  884.4  (just major-6th)
    32768:19683     =   882.4   -2.4 -->   396 \ 540  =  880.0  (pythagorean dim-7th)
       18:11        =   852.6   +0.7 -->   384 \ 540  =  853.3  (undecimal superminor[neutral]-6th)
       13:8         =   840.5   -0.5 -->   378 \ 540  =  840.0  (13th harmonic)
       21:13        =   830.3   +0.9 -->   374 \ 540  =  831.1  (tridecimal ?)
     6561:4096      =   815.6   +2.1 -->   368 \ 540  =  817.8  (pythagorean augmented-5th)
        8:5         =   813.7   -0.4 -->   366 \ 540  =  813.3  (just minor-6th)
      405:256       =   794.1   +1.4 -->   358 \ 540  =  795.6  (large just aug-5th)
      128:81        =   792.2   -1.1 -->   356 \ 540  =  791.1  (pythagorean minor-6th)
       11:7         =   782.5   -0.3 -->   352 \ 540  =  782.2  (undecimal augmented-5th)
       25:16        =   772.6   +0.7 -->   348 \ 540  =  773.3  (25th harmonic, small just augmented-5th)
       14:9         =   764.9   -0.5 -->   344 \ 540  =  764.4  (septimal subminor-6th)
       17:11        =   753.6   -0.3 -->   339 \ 540  =  753.3  (septendecimal diminished-6th)
       20:13        =   745.8   +0.9 -->   336 \ 540  =  746.7  (tridecimal augmented-5th)
      192:125       =   743.0   -0.8 -->   334 \ 540  =  742.2  (large just dim-6)
     1024:675       =   721.5   -1.5 -->   324 \ 540  =  720.0  (small just dim-6th)
        3:2         =   702.0   +0.3 -->   316 \ 540  =  702.2  (pythagorean perfect-5th)
    16384:10935     =   700.0   -2.2 -->   314 \ 540  =  697.8  (minimal just dim-6)
   262144:177147    =   678.5   -2.9 -->   304 \ 540  =  675.6  (pythagorean dim-6th)
       19:13        =   657.0   +0.8 -->   296 \ 540  =  657.8  (nondecimal doubly-augmented-4th)
       16:11        =   648.7   +0.2 -->   292 \ 540  =  648.9  (11th subharmonic, undecimal diminished-4th)
       13:9         =   636.6   -1.1 -->   286 \ 540  =  635.6  (tridecimal diminished-5th)
       23:16        =   628.3   +0.6 -->   283 \ 540  =  628.9  (23rd harmonic)
       10:7         =   617.5   +0.3 -->   278 \ 540  =  617.8  (septimal large-tritone)
      729:512       =   611.7   +1.6 -->   276 \ 540  =  613.3  (pythagorean augmented-4th)
       64:45        =   609.8   -0.9 -->   274 \ 540  =  608.9  (just diminished-5th)
       45:32        =   590.2   +0.9 -->   266 \ 540  =  591.1  (large just augmented-4th)
     1024:729       =   588.3   -1.6 -->   264 \ 540  =  586.7  (pythagorean diminished-5th)
        7:5         =   582.5   -0.3 -->   262 \ 540  =  582.2  (septimal small-tritone)
       25:18        =   568.7   +0.2 -->   256 \ 540  =  568.9  (small just aug-4th)
       18:13        =   563.4   +1.1 -->   254 \ 540  =  564.4  (tridecimal augmented-4th)
       11:8         =   551.3   -0.2 -->   248 \ 540  =  551.1  (11th harmonic, undecimal sub-augmented-4th)
       15:11        =   537.0   +0.8 -->   242 \ 540  =  537.8  (undecimal large-4th)
   177147:131072    =   521.5   +2.9 -->   236 \ 540  =  524.4  (pythagorean aug-3rd)
    10935:8192      =   500.0   +2.2 -->   226 \ 540  =  502.2  (large just aug-3rd)
        4:3         =   498.0   -0.3 -->   224 \ 540  =  497.8  (pythagorean perfect-4th)
      675:512       =   478.5   +1.5 -->   216 \ 540  =  480.0  (small just aug-3rd)
       21:16        =   470.8   +0.3 -->   212 \ 540  =  471.1  (21st harmonic, septimal-4th, 7*3)
       17:13        =   464.4   +0.0 -->   209 \ 540  =  464.4  (septendecimal 4th)
      125:96        =   457.0   +0.8 -->   206 \ 540  =  457.8  (minimal just aug-3rd)
       13:10        =   454.2   -0.9 -->   204 \ 540  =  453.3  (tridecimal diminished-4th)
        9:7         =   435.1   +0.5 -->   196 \ 540  =  435.6  (septimal supermajor-3rd)
       41:32        =   429.1   -0.2 -->   193 \ 540  =  428.9  (41st harmonic)
       32:25        =   427.4   -0.7 -->   192 \ 540  =  426.7  (small just dim-4th)
       14:11        =   417.5   +0.3 -->   188 \ 540  =  417.8  (undecimal diminished-4th)
       81:64        =   407.8   +1.1 -->   184 \ 540  =  408.9  (pythagorean major-3rd)
      512:405       =   405.9   -1.4 -->   182 \ 540  =  404.4  (minimal just dim-4)
        5:4         =   386.3   +0.4 -->   174 \ 540  =  386.7  (5th harmonic, just major-3rd)
     8192:6561      =   384.4   -2.1 -->   172 \ 540  =  382.2  (pythagorean diminished-4th)
       16:13        =   359.5   +0.5 -->   162 \ 540  =  360.0  (tridecimal major[neutral]-3rd)
       11:9         =   347.4   -0.7 -->   156 \ 540  =  346.7  (undecimal neutral-3rd)
       39:32        =   342.5   -0.3 -->   154 \ 540  =  342.2  (39th harmonic, 13*3)
    19683:16384     =   317.6   +2.4 -->   144 \ 540  =  320.0  (pythagorean augmented-2nd)
        6:5         =   315.6   -0.1 -->   142 \ 540  =  315.6  (just minor-3rd)
       19:16        =   297.5   +0.3 -->   134 \ 540  =  297.8  (19th harmonic)
     1215:1024      =   296.1   +1.7 -->   134 \ 540  =  297.8  (large just aug-2nd)
       32:27        =   294.1   -0.8 -->   132 \ 540  =  293.3  (pythagorean minor-3rd)
       13:11        =   289.2   -0.3 -->   130 \ 540  =  288.9  (tridecimal diminished-3rd)
       75:64        =   274.6   +1.0 -->   124 \ 540  =  275.6  (small just augmented-2nd)
        7:6         =   266.9   -0.2 -->   120 \ 540  =  266.7  (septimal subminor-3rd)
       37:32        =   251.3   -0.2 -->   113 \ 540  =  251.1  (37th harmonic)
       15:13        =   247.7   +1.1 -->   112 \ 540  =  248.9  (tridecimal augmented[neutral]-2nd)
      144:125       =   245.0   -0.5 -->   110 \ 540  =  244.4  (large just dim-3)
        8:7         =   231.2   -0.1 -->   104 \ 540  =  231.1  (septimal tone, supermajor-2nd)
      256:225       =   223.5   -1.2 -->   100 \ 540  =  222.2  (small just dim-3rd)
        9:8         =   203.9   +0.5 -->    92 \ 540  =  204.4  (pythagorean major-2nd \ tone)
     4096:3645      =   202.0   -2.0 -->    90 \ 540  =  200.0  (minimal just dim-3)
       10:9         =   182.4   -0.2 -->    82 \ 540  =  182.2  (just minor-tone)
    65536:59049     =   180.4   -2.7 -->    80 \ 540  =  177.8  (pythagorean dim-3rd)
       11:10        =   165.0   -0.6 -->    74 \ 540  =  164.4  (undecimal small-tone \ submajor-2nd)
       35:32        =   155.1   +0.4 -->    70 \ 540  =  155.6  (35th harmonic, 7*5)
       12:11        =   150.6   +0.5 -->    68 \ 540  =  151.1  (undecimal large-semitone)
       13:12        =   138.6   -0.8 -->    62 \ 540  =  137.8  (tridecimal minor-2nd)
       14:13        =   128.3   +0.6 -->    58 \ 540  =  128.9  (tridecimal major-2nd)
       15:14        =   119.4   +0.6 -->    54 \ 540  =  120.0  (septimal chromatic-semitone)
     2187:2048      =   113.7   +1.9 -->    52 \ 540  =  115.6  (pythagorean augmented-prime \ apotome)
       16:15        =   111.7   -0.6 -->    50 \ 540  =  111.1  (just diatonic-semitone)
       17:16        =   105.0   -0.5 -->    47 \ 540  =  104.4  (17th harmonic, septendecimal semitone)
      135:128       =    92.2   +1.2 -->    42 \ 540  =   93.3  (large just aug-prime)
      256:243       =    90.2   -1.3 -->    40 \ 540  =   88.9  (pythagorean minor-2nd \ limma)
       25:24        =    70.7   +0.4 -->    32 \ 540  =   71.1  (small just aug-prime, chromatic-semitone)
       33:32        =    53.3   +0.1 -->    24 \ 540  =   53.3  (33rd harmonic, 11*3)
      128:125       =    41.1   -1.1 -->    18 \ 540  =   40.0  (large just dim-2, diesis)
     2048:2025      =    19.6   -1.8 -->     8 \ 540  =   17.8  (small just dim-2nd, diaschisma)
    32805:32768     =     2.0   +2.5 -->     2 \ 540  =    4.4  (large just aug-7th, skhisma)
        1:1         =     0.0   +0.0 -->     0 \ 540  =    0.0  (prime, unison)

some commas:

3-limit
           ratio           cents   error              edo        cents      name

   531441:524288    =    23.5   +3.2 -->    12 \ 540  =   26.7  (pythagorean-comma)

5-limit
           ratio           cents   error              edo        cents      name

      648:625       =    62.6   -0.3 -->    28 \ 540  =   62.2  (major-diesis)
    16875:16384     =    51.1   +2.2 -->    24 \ 540  =   53.3  (negri-comma)
      250:243       =    49.2   -0.3 -->    22 \ 540  =   48.9  (maximal-diesis)
      128:125       =    41.1   -1.1 -->    18 \ 540  =   40.0  (enharmonic-diesis)
 34171875:33554432  =    31.6   +4.0 -->    16 \ 540  =   35.6  (ampersand-comma)
     3125:3072      =    29.6   +1.5 -->    14 \ 540  =   31.1  (magic-comma)
    20000:19683     =    27.7   -1.0 -->    12 \ 540  =   26.7  (tetracot-comma)
       81:80        =    21.5   +0.7 -->    10 \ 540  =   22.2  (syntonic-comma)
     2048:2025      =    19.6   -1.8 -->     8 \ 540  =   17.8  (diaschisma)
   393216:390625    =    11.4   -2.6 -->     4 \ 540  =    8.9  (wuerschmidt-comma)
  2109375:2097152   =    10.1   +3.3 -->     6 \ 540  =   13.3  (semicomma)
    15625:15552     =     8.1   +0.8 -->     4 \ 540  =    8.9  (kleisma)
    32805:32768     =     2.0   +2.5 -->     2 \ 540  =    4.4  (skhisma)
    76294:76256     =     0.9   -0.9 -->     0 \ 540  =    0.0  (ennealimma (~ratio))
   292300:292297    =     0.0  -26.7 -->   -12 \ 540  =  -26.7  (atom (~ratio))

7-limit
           ratio           cents   error              edo        cents      name

       36:35        =    48.8   +0.1 -->    22 \ 540  =   48.9  (septimal-diesis (9/5 : 7/4))
       49:48        =    35.7   -0.1 -->    16 \ 540  =   35.6  (slendro diesis (7/6 : 8/7))
       50:49        =    35.0   +0.6 -->    16 \ 540  =   35.6  (tritonic diesis, jubilisma (10/7 : 7/5))
       64:63        =    27.3   -0.6 -->    12 \ 540  =   26.7  (septimal-comma (16/9 : 7/4)
      225:224       =     7.7   +1.2 -->     4 \ 540  =    8.9  (septimal-kleisma (75/64 : 7/6)

11-limit
           ratio           cents   error              edo        cents      name

       22:21        =    80.5   -0.5 -->    36 \ 540  =   80.0  ((11/8 : 21/16))
       33:32        =    53.3   +0.1 -->    24 \ 540  =   53.3  (undecimal-diesis (11/8 : 4/3)
       45:44        =    38.9   +1.1 -->    18 \ 540  =   40.0  ((45/32 : 11/8))
     8192:8019      =    37.0   -1.4 -->    16 \ 540  =   35.6  (pyth dim-5th: 11/8)
       55:54        =    31.8   -0.7 -->    14 \ 540  =   31.1  ((11/8 : 27/20))
       56:55        =    31.2   -0.1 -->    14 \ 540  =   31.1  ((7/5 : 11/8))
       99:98        =    17.6   +0.2 -->     8 \ 540  =   17.8  (mothwellsma)
      100:99        =    17.4   +0.4 -->     8 \ 540  =   17.8  (ptolemisma)
      121:120       =    14.4   -1.0 -->     6 \ 540  =   13.3  (biyatisma (11/10 : 12/11))

13-limit
           ratio           cents   error              edo        cents      name

       27:26        =    65.3   +1.3 -->    30 \ 540  =   66.7  (pyth maj-6 : 13/8)
     1053:1024      =    48.3   +0.5 -->    22 \ 540  =   48.9  (13/8 : pyth min-6)
       40:39        =    43.8   +0.6 -->    20 \ 540  =   44.4  ((5/3 : 13/8))
       65:64        =    26.8   -0.2 -->    12 \ 540  =   26.7  ((13/8 : 8/5))
     6656:6561      =    24.9   -2.7 -->    10 \ 540  =   22.2  (13/8 : pyth aug-5th)
       91:90        =    19.1   -1.4 -->     8 \ 540  =   17.8  (superleap)
      144:143       =    12.1   +1.3 -->     6 \ 540  =   13.3  ((18/11 : 13/8))
      169:168       =    10.3   -1.4 -->     4 \ 540  =    8.9  (dhanvantarisma)

dexl (540-edo) calculator

Please make a donation to help keep Tonalsoft online.

Thank you!