A small interval used to separate two mappings that occur on the traditional Halberstadt keyboard. It usually occurs between the F and the F#. Its design is to accomodate two separate mappings, one on the white keys and one on the black keys, which maintain the approximate chromatic ordering of a 1/3-tone edo such as 17-edo or 18-edo.
To date [2005] there are two species of mappings which incorporate the brinko:
Lowering the 5-note mapping by an offset of about 130 cents works well, giving a brinko of ~12.8 cents, as illustrated below:
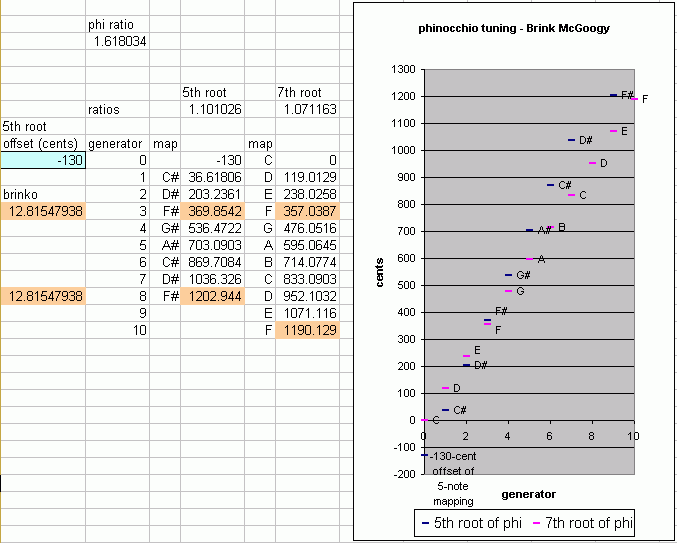
The phenomenon of the brinko was encountered in 1992 by Brink McGoogy.
The above example is one which exhibits the "asymmetrical brinko". When fitting together the two mappings (5-tone and 7-tone), the brinkos between F:F# and A#:B are mutually exclusive. Making one larger will always make the other smaller. If F and F# are made the same pitch (i.e., brinko = 0, as in a tuning created by Buzz Kimball before the brinko was discovered), A#:B is the maximum brinko size. If A# and B are the same pitch, F:F# is the maximum brinko size, and is the same as the previous case. Thus this is the full range of size of the brinko.
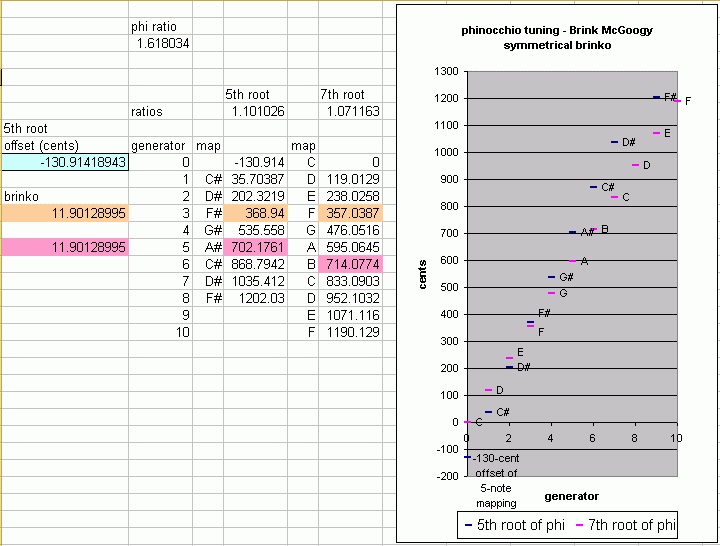
Brink's own preferred brinko tuning is a special case, analagous in some ways to 12-edo, and in other ways to meantone (so it's a sort of "mean-brinko"), is the symmetrical brinko tuning. Brink designed the symmetrical brinko tuning in which the brinko between F:F# is the same as the brinko between A#:B.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.