equal-temperament
a system of tuning based on a scale whose "steps" or degrees have logarithmically equal intervals between them, in contrast to the differently-spaced degrees of just intonation, fraction-of-a-comma-meantone, well-temperament, or other tunings. Generally abbreviated as ET.
Usually, but not always, equal temperaments assume octave-equivalence, of which the usual 12-edo is the most obvious example. For many theorists the preferred abbreviation or these types of temperaments is EDO, for which some other theorists substitute ED2; both of these specify that it is the 2:1 ratio which is to be equally divided.
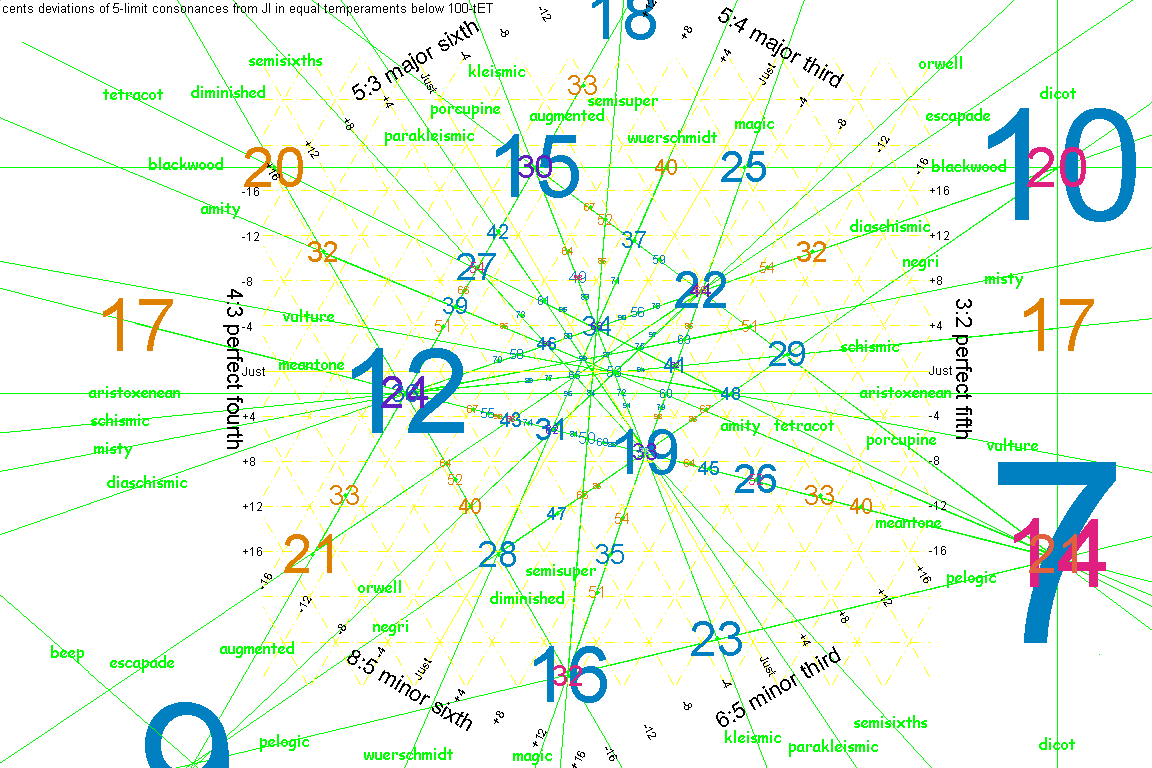
Below are some graphics by Paul Erlich, which show the amount of error for various EDOs for the basic concordant intervals in the 5-limit. The farther a point is from a given axis, the larger the errors in the tuning corresponding to the point, of the intervals corresponding to the axis. The basic concept is the same as that of Dalitz plots in physics, and the Chalmers tetrachord plots (see diagrams #3 and #4 on that page).
LEGEND:
- The yellow lines (barely legible) represent the just perfect 5th and its octave-complement the perfect 4th (ratios 3:2 and 4:3, respectively), and the just major 3rd / minor 6th (ratios 5:4 and 8:5, respectively) and minor 3rd / major 6th" (ratios 6:5 and 5:3, respectively), and the cents deviation from those ratios (the quantization in cents varies according to the zoom factor).
- The green lines connect EDOs which are collinear on this graph. When this happens, it indicates that a certain important small interval acting as a unison-vector is being tempered out, which is also known as "vanishing".
- It may be easier to view this using the negatives of Erlich's original graphics, so both are presented below. In the negatives, the blue lines represent the just ratios and the purple lines represent collinear EDOs. A small red square at the center which represents exact 5-limit JI has also been added to the negative images.
mouse-over the following links to zoom in to the desired scaling:
|
paul's originals zoom: 1 zoom: 10 zoom: 100 zoom: 1000 zoom: 10000 |
negatives zoom: 1 zoom: 10 zoom: 100 zoom: 1000 zoom: 10000 |
Below is a table listing each of the linear temperaments depicted in the diagrams above (in order of decreasing distance from the origin), and their associated vanishing commas. (Thanks to Carl Lumma for the original version of this table, and Paul Erlich for the current version)
|
temperament name(s) |
sample realizations {ET\per.\gen.} |
[2 3 5] map in terms of [per., gen.] |
[period, optimal gen.] (cents) |
optimum RMS error (cents) |
comma name(s) |
comma [2 3, 5> monzo |
comma ratio |
comma ~cents |
| father |
{3\3\1}, {5\5\2}, {8\8\3} |
[1,0] [2,-1] [2,1] |
[1200, 442.179356] |
45.614107 |
diatonic semitone |
[4 -1, -1> | 16 / 15 | 111.7 |
| beep |
{4\4\1}, {5\5\1}, {9\9\2} |
[1,0] [2,-2] [3,-3] |
[1200, 268.056439] |
35.60924 | large limma | [0 3, -2> | 27 / 25 | 133.2 |
| dicot |
{3\3\1}, {4\4\1}, {7\7\2}, {10\10\3} |
[1,0] [1,2] [2,1] |
[1200, 350.977500] |
28.851897 |
minor chroma, classic chromatic semitone |
[-3 -1, 2> | 25 / 24 | 70.67 |
| pelogic |
{7\7\3}, {9\9\4}, {16\16\7}, {23\23\10} |
[1,0] [2,-1] [1,3] |
[1200, 522.862346] |
18.077734 |
major chroma, major limma, limma ascendant |
[-7 3, 1> | 135 / 128 | 92.18 |
| blackwood |
{5\1\0}, {10\2\1}, {15\3\1}, {25\5\2} |
[5,0] [8,0] [12,-1] |
[240, 84.663787] |
12.759741 |
limma, pythagorean minor-2nd |
[8 -5, 0> | 256 / 243 | 90.22 |
|
diminished, 'octatonic' |
{4\1\0}, {8\2\1}, {12\3\1}, {16\4\1}, {28\7\2} |
[4,0] [6,1] [9,1] |
[300, 94.134357] |
11.06006 | major diesis | [3 4, -4> | 648 / 625 | 62.57 |
|
augmented, diesic |
{3\1\0}, {9\3\1}, {12\4\1}, {15\5\1}, {18\6\1}, {27\9\2}, {39\13\3}, {42\14\3} |
[3,0] [5,-1] [7,0] |
[400, 91.201856] |
9.677666 |
diesis, great diesis, minor diesis |
[7 0, -3> | 128 / 125 | 41.06 |
| porcupine |
{7\7\1}, {8\8\1}, {15\15\2}, {22\22\3}, {29\29\4}, {37\37\5}, {59\59\8} |
[1,0] [2,-3] [3,-5] |
[1200, 162.996026] |
7.975801 |
maximal diesis |
[1 -5, 3> | 250 / 243 | 49.17 |
| negri |
{9\9\1}, {10\10\1}, {19\19\2}, {28\28\3}, {29\29\3} |
[1,0] [2,-4] [2,3] |
[1200, 126.238272] |
5.942563 | - | [-14 3, 4> | 16875 / 16384 | 51.12 |
| magic (5-limit) |
{3\3\1}, {16\16\5}, {19\19\6}, {22\22\7}, {25\25\8}, {35\35\11}, {41\41\13}, {60\60\19}, {63\63\20}, {79\79\25} |
[1,0] [0,5] [2,1] |
[1200, 379.967949] |
4.569472 | small diesis | [-10 -1, 5> | 3125 / 3072 | 29.61 |
|
meantone, 'diatonic' |
{5\5\2}, {7\7\3}, {12\12\5}, {19\19\8}, {26\26\11}, {31\31\13}, {43\43\18}, {50\50\21}, {55\55\23}, {74\74\31}, {81\81\34} {131\131\55} |
[1,0] [2,-1] [4,-4] |
[1200, 503.835154] |
4.217731 |
comma, syntonic comma, comma of didymus |
[-4 4, -1> | 81 / 80 | 21.51 |
|
diaschismic, 5-limit pajara |
{10\5\1}, {12\6\1}, {22\11\2}, {34\17\3}, {46\23\4}, {56\28\5}, {58\29\5}, {70\35\6}, {78\39\7}, {80\40\7}, {90\45\8} |
[2,0] [3,1] [5,-2] |
[600, 105.446531] |
2.612822 | diaschisma | [11 -4, -2> | 2048 / 2025 | 19.55 |
| tetracot |
{7\7\1}, {27\27\4}, {34\34\5}, {41\41\6}, {48\48\7}, {61\61\9}, {75\75\11} |
[1,0] [1,4] [1,9] |
[1200, 176.282270] |
2.504205 |
minimal diesis |
[5 -9, 4> | 20000 / 19683 | 27.66 |
| aristoxenean |
{12\1\0}, {48\4\1}, {60\5\1}, {72\6\1}, {84\7\1}, {96\8\1} |
[12,0] [19,0] [28,-1] |
[100, 14.663787] |
1.382394 |
pythagorean comma |
[-19 12, 0> | 531441 / 524288 | 23.46 |
| semisixths |
{19\19\7}, {27\27\10}, {46\46\17}, {65\65\24}, {73\73\27}, {84\84\31} |
[1,0] [-1,7] [-1,9] |
[1200, 442.979297] |
1.157498 | - | [2 9, -7> | 78732 / 78125 | 13.40 |
| würschmidt |
{28\28\9}, {31\31\10}, {34\34\11}, {37\37\12}, {65\65\21}, {71\71\23}, {96\96\31}, {99\99\32} |
[1,0] [-1,8] [2,1] |
[1200, 387.819673] |
1.07195 |
würschmidt's comma |
[17 1, -8> | 393216 / 390625 | 11.45 |
|
kleismic, hanson |
{15\15\4}, {19\19\5}, {23\23\6}, {34\34\9}, {53\53\14}, {72\72\19}, {83\83\22}, {87\87\23}, {91\91\24}, {125\125\33} |
[1,0] [0,6] [1,5] |
[1200, 317.079675] |
1.029625 | kleisma | [-6 -5, 6> | 15625 / 15552 | 8.107 |
| misty |
{12\4\1}, {63\21\5}, {75\25\6}, {87\29\7}, {99\33\8} |
[3,0] [5,-1] [6,4] |
[400, 96.787939] |
0.905187 | - | [26 -12, -3> | 67108864 / 66430125 | 17.60 |
| orwell (5-limit) |
{9\9\2}, {22\22\5}, {31\31\7}, {53\53\12}, {75\75\17}, {84\84\19}, {97\97\22}, {128\128\29}, {243\243\55} |
[1,0] [0,7] [3,-3] |
[1200, 271.589600] |
0.80041 | semicomma | [-21 3, 7> | 2109375 / 2097152 | 10.06 |
| escapade |
{22\22\1}, {43\43\2}, {65\65\3}, {87\87\4}, {152\152\7}, {217\217\10} |
[1,0] [2,-9] [2,7] |
[1200, 55.275493] |
0.483108 | - | [32 -7, -9> | 4.2949E+9 / 4.2714E+9 | 9.492 |
| amity |
{7\7\2}, {39\39\11}, {46\46\13}, {53\53\15}, {60\60\17}, {99\99\28}, {152\152\43}, {205\205\58}, {311\311\88} |
[1,0] [3,-5] [6,-13] |
[1200, 339.508826] |
0.383104 | - | [9 -13, 5> | 1600000 / 1594323 | 6.154 |
| parakleismic |
{19\19\5}, {42\42\11}, {61\61\16}, {80\80\21}, {99\99\26}, {118\118\31}, {217\217\57} |
[1,0] [5,13] [6,-14] |
[1200, 315.250913] |
0.276603 | parakleisma | [8 14, -13> | 1.2244E+9 / 1.2207E+9 | 5.292 |
| semisuper |
{16\8\1}, {18\9\1}, {34\17\2}, {50\25\3}, {84\42\5}, {118\59\7}, {152\76\9}, {270\135\16}, {388\194\23} |
[2,0] [4,-7] [5,-3] |
[600, 71.146064] |
0.194018 | - | [23 6, -14> | 6.1152E+9 / 6.1035E+9 | 3.338 |
|
schismic, helmholtz/groven |
{12\12\5}, {29\29\12}, {41\41\17}, {53\53\22}, {65\65\27}, {118\118\49}, {171\171\71}, {200\200\83}, {301\301\125} |
[1,0] [2,-1] [-1,8] |
[1200, 498.272487] |
0.161693 | schisma | [-15 8, 1> | 32805 / 32768 | 1.954 |
| vulture |
{48\48\19}, {53\53\21}, {58\58\23}, {217\217\86}, {270\270\107}, {323\323\128} |
[1,0] [0,4] [-6,21] |
[1200, 475.542233] |
0.153767 | - | [24 -21, 4> | 1.0485E+10 / 1.0460E+10 | 4.200 |
| enneadecal |
{19\1\0}, {152\8\1}, {171\9\1}, {323\17\2}, {494\26\3}, {665\35\4} |
[19,0] [30,1] [44,1] |
[63.157894, 7.292252] |
0.104784 |
'19-tone comma' |
[-14 -19, 19> | 1.9074E+13 / 1.9043E+13 | 2.816 |
| semithirds |
{118\118\19}, {205\205\33}, {323\323\52}, {441\441\71}, {559\559\90}, {1000\1000\161} |
[1,0] [4,-15] [2, 2] |
[1200, 193.199615] |
0.060822 | - | [38 -2, -15> | 2.7488E+11 / 2.7466E+11 | 1.384 |
| vavoom |
{75\75\7}, {118\118\11}, {311\311\29}, {547\547\51}, {665\665\62}, {901\901\84} |
[1,0] [0,17] [4,-18] |
[1200, 111.875426] |
0.058853 | - | [-68 18, 17> | 2.9558E+20 / 2.9515E+20 | 2.523 |
| tricot |
{53\53\25}, {388\388\183}, {441\441\208}, {494\494\233}, {547\547\258}, {600\600\283} |
[1,0] [3,-3] [16,-29] |
[1200, 565.988015] |
0.0575 | - | [39 -29, 3> | 6.8720E+13 / 6.8630E+13 | 2.246 |
| counterschismic |
{53\53\22}, {306\306\127}, {730\730\303} |
[1 0], [2,-1], [21,-45] |
[1200, 498.082318] |
0.026391 | - | [-69 45, -1> | 2.9543E+21 / 2.9515E+21 | 1.661 |
|
ennealimmal (5-limit) |
({9\1\0},) {72\8\3), {99\11\4}, {171\19\7}, {243\27\10}, {270\30\11}, {441\49\18}, {612\69\25} |
[9,0] [15,-2] [22,-3] |
[133.333333, 49.008820] |
0.025593 | ennealimma | [1 -27, 18> | 7.6294E+12 / 7.6256E+12 | 0.862 |
| minortone |
{46\46\7}, {125\125\19}, {171\171\26}, {217\217\33}, {388\388\59}, {559\559\85}, {730\730\111}, {901\901\137} |
[1,0] [-1,17] [-3,35] |
[1200, 182.466089] |
0.025466 | - | [-16 35, -17> | 5.0032E+16 / 5.0000E+16 | 1.092 |
| kwazy |
{118\59\16}, {494\247\67}, {612\306\83}, {730\365\99}, {1342\671\182} |
[2,0] [1,8] [6,-5] |
[600, 162.741892] |
0.017725 | - | [-53 10, 16> | 9.0102E+15 / 9.0072E+15 | 0.569 |
| astro |
{118\118\13}, {1171\1171\129}, {2224\2224\245} |
[1,0] [5,-31] [1,12] |
[1200, 132.194511] |
0.014993 | - | [91 -12, -31> | 2.4759E+27 / 2.4747E+27 | 0.815 |
| whoosh |
{441\441\206}, {730\730\341}, {1171\1171\547}, {1901\1901\888}, {3072\3072\1435} |
[1,0] [17,-33] [14,-25] |
[1200, 560.546970] |
0.012388 | - | [37 25, -33> | 1.1645E+23 / 1.1642E+23 | 0.522 |
| monzismic |
{53\53\11}, {559\559\116}, {612\612\127}, {665\665\138}, {1171\1171\243}, {1783\1783\370} |
[1,0] [2,-2] [10,-37] |
[1200, 249.018448] |
0.005738 | monzisma | [54 -37, 2> | 4.5036E+17 / 4.5028E+17 | 0.292 |
| egads |
{441\441\116}, {901\901\237}, {1342\1342\353}, {1783\1783\469}, {3125\3125\822} |
[1,0] [15,-51] [16,-52] |
[1200, 315.647874] |
0.00466 | - | [-36 -52, 51> | 4.4409E+35 / 4.4400E+35 | 0.339 |
| fortune |
{612\612\113}, {1901\1901\351}, {2513\2513\464}, {3125\3125\577} |
[1,0] [-1,14] [11,-47] |
[1200, 221.567865] |
0.003542 | - | [-107 47, 14> | 1.6229E+32 / 1.6226E+32 | 0.277 |
| senior |
{171\171\46}, {1000\1000\269}, {1171\1171\315}, {1342\1342\361}, {2513\2513\676}, {3684\3684\991} |
[1,0] [11,-35] [19,-62] |
[1200, 322.801387] |
0.003022 | - | [-17 62, -35> | 3.8152E+29 / 3.8147E+29 | 0.230 |
| gross |
{118\118\9}, {1783\1783\136}, {1901\1901\145}, {3684\3684\281} |
[1,0] [-2,47] [4,-22] |
[1200, 91.531021] |
0.002842 | - | [144 -22, -47> | 2.2301E+43 / 2.2298E+43 | 0.245 |
| pirate |
{730\730/113}, {1783\1783\276}, {2513\2513\389}, {4296\4296\665} |
[1,0] [-6,49] [0,15] |
[1200, 185.754179] |
0.000761 | - | [-90 -15, 49> | 1.7764E+34 / 1.7763E+34 | 0.047 |
| raider |
{1171\1171\335}, {3125\3125\894}, {4296\4296\1229} |
[1,0] [-9,37] [-26,99] |
[1200, 343.296099] |
0.000511 | - | [71 -99, 37> | 1.71799E+47 / 1.71793E+47 | 0.062 |
| atomic |
({12\1\0},) {600\50\1}, {612\51\1}, {3072\256\5}, {3684\307\6}, {4296\358\7} |
[12,0] [19,1] [28,-7] |
[100, 1.955169] |
0.00012 |
atom of kirnberger |
[161 -84, -12> | 2.92300E+48 / 2.92298E+48 | 0.015 |
Below is a lattice diagram of these "vanishing commas". Paul has included all the ones listed in the table above with numerator and denominator of seven digits or fewer. (Compare this diagram with those on Monzo, 5-limit intervals, 100 cents and under.)
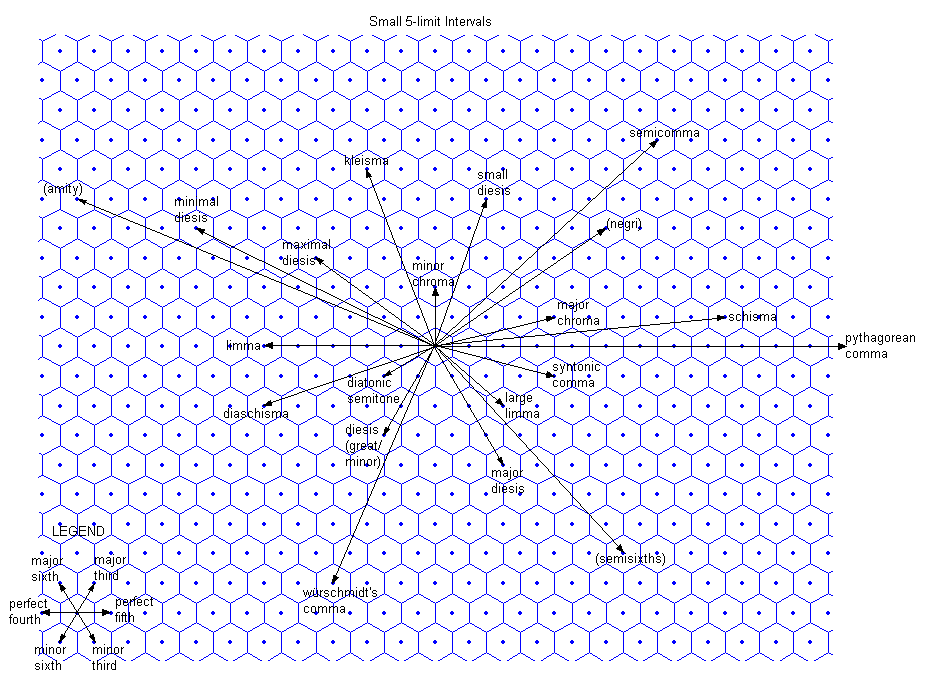
It's my belief that the vectors of these intervals play a role in the patterns of shading and coloring in my gallery of EDO 5-limit error lattices. Those lattices have the 3 and 5 axes oriented exactly as here.
This analysis only concerns the representations of various EDOs to the 5-limit. See Monzo, EDO prime-error to get an idea of how different EDOs represent all of the prime factors from 3 to 43.
Examples of non-octave equal temperaments are Gary Morrison's 88-CET (88 cents between degrees), the Bohlen-Pierce scale, and Wendy Carlos's alpha, beta, and gamma scales [audio examples on the Wendy Carlos site].
In a post to the Early Music list, Aleksander Frosztega wrote:
P.S. [quoting] >The phrase "equal temperament" has existed in print since 1781. French used the term "temperament egal" long before 1781.
German writers used the phrase gleichschwebende Temperatur to denote equal-beating temperament since the beginning of the 18th century. This is not to be confused with equal-temperament, and instead actually denotes certain meantones, well-temperament, and other tunings where the varying temperings of different intervals results in them having equal numbers of beats per second. However, most German writers have in fact used the term (and its variant spellings gleich schwebende Temperatur and gleich-schwebende Temperatur) to designate regular 12-edo, and unless the context specifically indicates that a well-temperament or meantone is under discussion, gleichschwebende Temperatur in German treatises generally refers to 12-edo.
(Note also Schoenberg's frequent use, in his Harmonielehre, of the term schwebend to refer to a method of composition in which the sense of tonality is "suspended, floating", thus leading the way to his style of pantonality beginning around 1908.)
Below is a table showing advocates of various "octave"-based ETs, with approximate dates. It does not claim to be complete, and keeps growing. (click on the highlighted numbers to show more detail about those ETs)
| ET | Date and Theorist/composer |
| 5 |
the smallest cardinality EDO which has any real musical usefulness, some theorists describe Indonesian slendro scale as this 2001 -- Herman Miller |
| 6 |
the "whole-tone scale" 1787 -- Wolfgang A. Mozart (in his A Musical Joke) 1894 -- Claude Debussy 1902 -- Arnold Schönberg |
| 7 |
traditional Thai music 1991 -- Clem Fortuna 1997 -- Randy Winchester 2001 -- Robert Walker |
| 8 |
1980 -- Gordon Mumma (Octal Waltz for harpsichord) 1981 -- Daniel Wolf 1997 -- Randy Winchester |
| 9 |
early 1900s -- Charles Ives (in Monzo, Ives "stretched" scales) 1930s-60s -- R. M. A. Kusumadinata (Sunda: mapping of 3 pathet onto 7-out-of-9-equal) 19?? -- James Tenney (piano part, The Road to Ubud) |
| 10 |
1930s-60s -- R. M. A. Kusumadinata (Sunda) 1990s -- Elaine Walker 1978 -- Gary Morrison 1997 -- Randy Winchester 1998 -- William Sethares |
| 11 |
1996 -- Daniel Wolf |
| 12 |
semitone or "half-step" before 3000 BC -- a possible Sumerian tuning (according to Monzo, Speculations on Sumerian Tuning) 1584 -- Prince Chu Tsai-yü (China) 1585 -- Simon Stevin (Netherlands) 1636 -- Marin Mersenne c.1780-1828 -- Mozart, Beethoven, and Schubert compose many chord progressions which, by the use of enharmonic equivalence of the diesis, strongly imply 12-edo or a related 12-tone "circulating" well-temperament 1802 -- Georg Joseph Vogler 1817 -- Gottfried Weber 1900-1999 -- the nearly universal tuning of the 'developed' world 1911 -- Arnold Schönberg (along with his personal rejection of microtonality) |
| 13 |
1962 -- Ernst Krenek (opera Ausgerechnet und Verspielt, op. 179) 1991 -- Paul Rapoport 1998 -- Herman Miller 1999 -- Dan Stearns 2001 -- X. J. Scott |
| 14 |
1990 -- Ralph Jarzombek 2000 -- Herman Miller |
| 15 |
1930s-60s -- R. M. A. Kusumadinata (Sunda) 1951 -- Augusto Novaro 1983 -- Joe Zawinul, on Molasses Run from Weather Report album Procession 1991 -- Easley Blackwood 1991 -- Clem Fortuna 1996 -- Herman Miller 1997 -- Randy Winchester 1998 -- Paul Erlich, with the group MAD DUXX (link to .ram audio file) 2001 -- Francesco Caratolozzo |
| 16 |
1930s-60s -- R. M. A. Kusumadinata (Sunda) 1971 -- David Goldsmith 1993 -- Steve Vai 1997 -- Randy Winchester 1998 -- Herman Miller 2002 -- Victor Cerullo |
| 17 |
1653 -- Brouncker 1809 -- Villoteau (describing Arabic tuning) 1929 -- Malherbe 1935 -- Karapetyan 1960s -- Ivor Darreg 1997 -- Herman Miller 1999 -- Margo Schulter (as a pseudo-Pythagorean tuning) |
| 18 |
1907 -- Ferrucio Busoni (in his theory, but not used in his compositions) 1940s -- Julián Carrillo, 1/3rd-tone piano 1960s -- Ivor Darreg |
| 19 |
third-tone (the tuning normally meant by that term) 1558 -- Guillaume Costeley 1577 -- Salinas (19 notes of '1/3-comma meantone', almost identical to 19-ET) before 1633 -- Jean Titelouze ('third-tones' may describe 19-ET) 1835 -- Wesley Woolhouse (the most practical approximation of his 'optimal meantone') 1852 -- Friedrich Opelt 1911 -- Melchiorre Sachs 1921 -- José Würschmidt 1922 -- Thorwald Kornerup 1925 -- Ariel 1926 -- Jacques Handschin 1932 -- Joseph Yasser 1940s -- Tillman Schafer 1961 -- M. Joel Mandelbaum 1960s -- Ivor Darreg 1976 -- Henri Pousseur: Racine 19e de 8/4, pour violoncelle seul 1979 -- Yunik & Swift 1979 -- Jon Catler 19?? -- Matthew Puzan 198? -- Erik Griswold 1987 -- Herman Miller 1996 -- Neil Haverstick 1990s -- Elaine Walker 1990s -- Jonathan Glasier 1990s -- William Casey Wesley 1998 -- Joseph Monzo (19-tone Samba) 1999 -- John Starrett 2004 -- Aaron Krister Johnson |
| 20 |
1980 -- Gerald Balzano 1996 -- Paul Zweifel 1999 -- Herman Miller |
| 21 |
2001 -- Herman Miller |
| 22 |
(some older theories describe the Indian sruti system as this -- an interpretation now considered erroneous; it is now recognized that the steps are unequal) 1877 -- Bosanquet 1921 -- José Würschmidt (for the future, after 19 runs its course) (1960s -- Erv Wilson -- used modulus-22, not necessarily EDO) 1960s -- Ivor Darreg 1980 -- Morris Moshe Cotel 1993 -- Paul Erlich 1997 -- Steve Rezsutek -- customized guitars and a keyboard for Paul Erlich's 22edo scales 1997 -- Randy Winchester 1999 -- Herman Miller 1999 -- Peter Blasser 2000 -- Alison Monteith |
| 23 |
some theorists describe Indonesian pelog scale as subset of this 1920s -- Hornbostel (describing Burmese music) |
| 24 |
quarter-tone: 21 (= 2) quarter-tones per Semitone; 12 * 21 = 24 quarter-tones per octave. Also called enamu (1mu), a MIDI pitch-bend unit. 1760 - Charles Delusse: Air a la Greque (earliest notation of microtonal pitches in the "common-practice" era) 1849 - Fromental Halévy - his cantata Prométhée enchaîné uses quarter-tones between B:C and E:F, to revive the ancient enharmonic genus. 1890s -- John Foulds 1895 -- Julián Carrillo: String Quartet 1906 -- Richard H. Stein (first published 24-tET scores) 1906 -- Arnold Schönberg (schematic sketch, no extant compositions) 1908 -- Anton Webern (early drafts of two songs) 1916 -- Charles Ives 1917 -- Willi von Möllendorff 1918 -- Jörg Mager 1920 -- Alois Hába (and subsequently many of his students) 1924 -- Julián Carrillo 1932 -- adopted as standard tuning in Egypt and elsewhere in Arabic world 1933 -- Ivan Wyschnegradsky (Treatise on Quartertone Harmony) 1940s -- Julián Carrillo, 1/4th-tone piano 1941 -- Mildred Couper 1948 -- Pierre Boulez (original version of Le Soleil des Eaux) 1950s -- Giacinto Scelsi (very loosely-conceived intonation) 1967 -- Tui St. George Tucker 1969 -- Györgi Ligeti (Ramifications) 1960s-2000s -- John Eaton 1980s -- Brian Ferneyhough (very loosely-conceived intonation) 1983 -- Leo de Vries 1994 -- Joseph Monzo, 24-eq tune |
| 25 |
1994 -- Paul Rapoport |
| 26 |
1998 -- Paul Erlich 1998 -- Herman Miller |
| 27 |
2001 -- Gene Ward Smith 2001 -- Herman Miller |
| 28 |
1997 -- Paul Erlich (for music based on the diminished scale) |
| 29 |
by 1875 -- Émile Chevé (by mistake) |
| 30 |
1940s -- Julián Carrillo, 1/5th-tone piano |
| 31 |
diesis (one of several meanings of that term) 1555 -- Nicola Vicentino (31 notes of extended meantone nearly identical to 31-ET) 1606 -- Vito Trasuntino (31 notes of extended meantone nearly identical to 31-ET) 1606 -- Gonzaga (31 notes of extended meantone nearly identical to 31-ET) before 1618 -- Scipione Stella (31 notes of extended meantone nearly identical to 31-ET) 1618 -- Fabio Colonna (31 notes of extended meantone nearly identical to 31-ET) 1623 -- Daniel Hizler (used only 13 out of 31-ET in practice) 1666 -- Lemme Rossi 1691 -- Christiaan Huygens 1722 -- Friedrich Suppig 1725 -- Ambrose Warren 1739 -- Quirinus van Blankenburg (as a system of measurement) 1754 -- J. E. Gallimard 1818 -- Pierre Galin 1860s -- Josef Petzval 1917-19 -- P. S. Wedell (quoted by Kornerup) 1930 -- Thorvald Kornerup 1932 -- Joseph Yasser (for the future, after 19 runs its course) 1941 -- Adriaan Fokker 1947 -- Mart. J. Lürsen 1950s -- Henk Badings (and many other Dutch composers) (1960s -- Erv Wilson used modulus-31, not necessarily ET) 1962 -- Joel Mandelbaum (opera Dybbuk) 1967 -- Alois Hába 1970s -- Dr. Abram M. Plum 1973 -- Leigh Gerdine 1974 -- Sebastian von Hörner 1975 -- George Secor 1979 -- Jon Catler 1980s -- Brian Ferneyhough (very loosely-conceived intonation) 1989 -- John Bischoff and Tim Perkis 1999 -- Paul Erlich |
| 34 |
1979 -- Dirk de Klerk before 1998 -- Larry Hanson 1997 -- Neil Haverstick |
| 36 |
sixth-tone; 3 units per Semitone = 12 * 3 units per "octave" 1907 -- Ferrucio Busoni (in his theory, but not used in compositions) 1923-1960s -- Alois Hába 1940s -- Julián Carrillo, 1/6th-tone piano 1952 -- Henri Pousseur: Prospection, pour un piano-triple à sixièmes de ton by 1997 -- Tomasz Liese -- 19-out-of-36-edo subset scale 2010 -- Joseph Monzo -- using 83 degrees to map prime-factor 5 (best mapping of 5 is to 84 degrees - exactly the same size as 12-edo). |
| 37 |
2012 -- Joseph Monzo -- very strong approximation of factors 5,7,11,13 in 13-limit JI. |
| 38 |
2004 -- tuning-math group, for situations where introducing a period of 1/2 or splitting the fifth into two over 19-equal might be useful. 2^(11/38) is almost precisely an 11/9. |
| 41 |
1901 -- Paul von Jankó (1960s -- Erv Wilson claims that Partch was intuitively feeling out 41-ET) 1975 -- George Secor 1989 -- Helen Fowler 1993 -- Joseph Monzo 1998 -- Carl Lumma 1998 -- Patrick Ozzard-Low 2002 -- Gene Ward Smith |
| 42 |
1940s -- Julián Carrillo, 1/7th-tone piano |
| 43 |
méride 1701 -- Joseph Sauveur - a unit of interval measurement, nearly identical to 1/5-comma meantone |
| 46 |
1989 -- R. Fuller 1998 -- Graham Breed 2000 -- Dave Keenan and Paul Erlich 2002 -- Gene Ward Smith |
| 48 |
doamu (2mu), a MIDI pitch-bend unit: 22 (= 4) 2mus per Semitone = 12 * 22 = 48 2mus per octave. Also called "eighth-tone". early 1900s -- Charles Ives (according to Monzo, Ives stretched-octave scales) 1915 -- N. Kulbin 1924 -- Julián Carrillo 1940s -- Julián Carrillo, 1/8th-tone piano 19?? -- Patrizio Barbieri 19?? -- Claus-Steffen Mahnkopf 19?? -- Volker Staub 1998 -- Joseph Pehrson |
| 50 |
(1558 -- Zarlino - fair approximation to 2/7-comma meantone, the first meantone to be described with mathematical exactitude) 1710 -- Konrad Henfling 1759 -- Robert Smith (as an approximation to his ideal 5/18-comma meantone system) 1835 -- Wesley Woolhouse (as practical approximation to his 7/26-comma 'optimal meantone') 1940s -- Tillman Schafer |
| 53 |
mercator; nearly identical to pythagorean tuning and a very good approximation to 5-limit just intonation 400s BC -- Implied by Philolaus (disciple of Pythagoras) 200s BC -- King Fang 1608 -- Nicolaus Mercator (only as a system of measurement, not intended to be used on an instrument) 1650 -- Athanasius Kircher (1713 -- 53-tone Pythagorean tuning became official scale in China) 1874-75 -- R. H. M. Bosanquet 1875 -- Alexander J. Ellis (appendix to Helmholtz, On the Sensations of Tone) 1890 -- Shohé Tanaka c.1900 -- Standard Turkish music-theory 1911 -- Robert Neumann (quoted by Schönberg in Harmonielehre) 1927 -- Augusto Novaro 1978 -- Larry Hanson 2002 -- Gene Ward Smith 2005 -- Chris Mohr |
| 54 |
1940s -- Julián Carrillo, 1/9th-tone piano |
| 55 |
(good approximation to 1/6-comma meantone) 1711 -- Joseph Sauveur, "the system which ordinary musicians use" before 1722 -- Johann Beer 1723 -- Pier Francesco Tosi before 1748 -- Georg Philip Telemann 1748 -- Georg Andreas Sorge 1752 -- Johann Joachim Quantz 1755 -- Estève 1780s -- W. A. Mozart, subsets of up to 20 tones, for non-keyboard instruments (according to Monzo, Mozart's Tuning) |
| 58 |
(1770 -- Dom François Bedos de Celles - according to Barbour, but this may be erroneous. See Yahoo tuning message 63618) 2002 -- Gene Ward Smith |
| 60 |
5 units per Semitone = 12 * 5 units per "octave". 1940s -- Julián Carrillo, 1/10th-tone piano 1980s? -- Richard Boulanger |
| 65 |
1927 -- Augusto Novaro 1951 -- J. Murray Barbour, as a 5-limit system. 2004 -- Gene Ward Smith, it is simultaneously a schismatic system and a semisixths (78732/78125 comma) system. |
| 66 |
1940s -- Julián Carrillo, 1/11th-tone piano |
| 68 |
1847 -- Meshaqah (describing modern Greek tuning) 1989? -- John Chalmers (describing Byzantine tuning) |
| 72 |
twelfth-tone / moria; 6 units per Semitone = 12 * 6 units per "octave". 1800s -- standard quantization for Byzantine Chant 1927 -- Alois Hába (in his book Neue Harmonielehre) 1927 -- Augusto Novaro 1938-58 -- Evgeny Alexandrovich Murzin created a 72-tET synthesizer. Among composers to write for it: Andrei Volkonsky, Nikolai Nikolsky, Eduard Artemiev, Alexander Nemtin, Andrei Eshpai, Gennady Gladkov, Pyotr Meshchianinov, Stanislav Kreichi (see Anton Rovner's article in TMA). 1940s -- Julián Carrillo, 1/12th-tone piano 1953 -- Ivan Wyschnegradsky 1963 -- Iannis Xenakis (cf. his book Musiques formelles) 1970 -- Ezra Sims 1970 -- Franz Richter Herf 1970 -- Rolf Maedel 1970s-2000s -- Joe Maneri (and subsequently many of his students) 1980s? -- James Tenney 1990s -- Ted Mook 1999 -- Paul Erlich 1999 -- Joseph Monzo (as basis of simplified HEWM notation) 1999 -- Rick Tagawa 2001 -- Dave Keenan, Graham Breed, Joseph Pehrson, Paul Erlich, Joseph Monzo (for notation of miracle family scales) 2001 -- Julia Werntz 2002 -- Gene Ward Smith |
| 74 |
1762 -- Riccati (approximation to 3/14-comma meantone) 1855 -- Drobisch (approximation to 2/9-comma meantone) 1991 -- John Cage, in "Ten" for chamber ensemble |
| 76 |
1998 -- Paul Erlich (as a unified tuning for various tonal systems) |
| 78 |
1940s -- Julián Carrillo, 1/13th-tone piano |
| 80 |
2004 -- Gene Ward Smith - a strong 19-limit system. Chains of 80-edo fifths have been proposed for neo-Gothic or Arabic inspired music. |
| 81 |
2002 -- Joseph Monzo, good approximation to Kornerup's "golden meantone" 2005 -- Gene Ward Smith, approximation to 5/19-comma meantone |
| 84 |
7 units per Semitone = 12 * 7 units per "octave". 1940s -- Julián Carrillo, 1/14th-tone piano 1985 -- Harald Waage (for 5-limit just intonation) |
| 87 |
1951 -- J. Murray Barbour, as a 5-limit system 1998 -- Paul Erlich - it is consistent and unique in the 13-odd-limit 2004 -- Gene Ward Smith, it supports kleismic tempering 2020 -- Jeff Brown |
| 88 |
for most purposes, essentially the same as LucyTuning. 1775 -- John "Longitude" Harrison 1987 -- Charles Lucy |
| 90 |
1940s -- Julián Carrillo, 1/15th-tone piano |
| 94 |
unique up to 13-odd-limit, and consistent up to 23-odd-limit 1998 -- Paul Erlich 2015 -- Cam Taylor |
| 96 |
triamu (3mu), a MIDI pitch-bend unit: 23 (= 8) 3mus per Semitone = 12 * 23 = 96 3mus per "octave". Also called "1/16-tone". 1924 -- Julián Carrillo 1940s -- Julián Carrillo, 1/16th-tone piano 1980 -- Pascale Criton 2001 -- Vincent-Olivier Gagnon |
| 99 |
2004 -- Gene Ward Smith, 99-edo is significant as a 7-limit system, having commas of 2401/2400, 3136/3125 and 4375/4374. Its errors, well under 2 cents, are by some people's ears just enough to be pleasing. |
| 100 |
1980s -- Barry Vercoe - built into CSound software |
| 106 |
2 * 53 degrees per "octave" 2004 -- Joseph Monzo (in analyzing Philolaus's small intervals) |
| 111 |
2004 -- Gene Ward Smith - strong 13-21-limit system |
| 118 |
1874-5 -- Bosanquet |
| 130 |
2004 -- Gene Ward Smith - twice 65, and important in the 7, 13 (and 15) limits in particular. |
| 140 |
2004 -- Gene Ward Smith, mentioned in a manner of speaking by Edward Charles Titchmarsh in his book The Theory of the Riemann Zeta Function, where he discusses a high value of the Riemann zeta function which corresponds to the 140 division. It is an important 7-limit division. |
| 144 |
farab; 12 units per Semitone = 12 * 12 units per "octave". 300s BC -- Aristoxenus (most likely interpretation of his theories) early 900s -- Abu Nasr al-Farabi 1946 -- Joseph Schillinger 1999 -- Dan Stearns and Joseph Monzo (chiefly for its value as a unified notation for mixed EDOs and/or complex just intonation tunings) |
| 152 |
1999(?) -- Paul Erlich, "Universal Tuning" |
| 171 |
(19?? -- Eivend Groven - approximated by his 1/8-skhisma temperament) 1926 -- Perrett 1975 -- Martin Vogel 2002 -- Gene Ward Smith |
| 175 |
2002 -- Gene Ward Smith |
| 192 |
tetramu (4mu), a MIDI pitch-bend unit: 24 (= 16) 4mus per Semitone = 12 * 24 = 192 4mus per octave. |
| 200 |
16 2/3 degrees per Semitone 2002 -- Joseph Monzo (in analyzing Werckmeister III) |
| 205 |
meme 2001 -- Aaron Hunt: 205 = 41 x 5 = [(7 x 6) - 1] x 5 = (12 x 17) + 1; used as the basis tuning for his Tonal Plexus microtonal keyboard |
| 217 |
7 * 31 degrees per octave = 18 1/12 degrees per Semitone 2002 -- Joseph Monzo (proposed for adaptive-JI tuning of Mahler's compositions) 2002 -- Bob Wendell (for quantification of just intonation to facilitate composing in a polyphonic blues style) 2002 -- George Secor & Dave Keenan (as a basis for notation for JI and multi-EDOs) |
| 224 |
2004 -- Gene Ward Smith, it is important in the 13-limit in particular. 2004 -- George Secor, as an important part of Sagittal notation |
| 270 |
tredek; named by Joseph Monzo in accordance with its excellent approximation of 13-limit JI 1970s? -- Erv Wilson and John Chalmers 1997 -- Paul Hahn 2013 -- Joseph Monzo -- for use as a unit of interval measurement without need for decimal places, strongest 3-digit EDO for 13-limit JI. |
| 288 |
early 1900s -- Charles Ives (as analyzed in Monzo, Ives stretched octave scales) |
| 300 |
25 units per Semitone = 12 * 25 units per "octave". 1800s -- system of savarts |
| 301 |
1701 -- Joseph Sauveur - heptameride (for ease of calculation with logs: log(2)~=0.301; and because 301 is divisible by 43) before 1835 -- Captain J. W. F. Herschel (cited by Woolhouse) |
| 311 |
gene; named by Joseph Monzo both in honor of Gene Ward Smith and for its connotation of a basic biological unit 2004 -- Gene Ward Smith - this remarkable division is important in the 13 through 41 limits, in every one of those odd limits. As a generic way of representing what some might maintain is anything anyone could reasonably want to represent it is of interest. 2007 -- Joseph Monzo -- for use as a unit of interval measurement without need for decimal places, very strong thru 41-limit JI. |
| 318 |
1999 -- Joseph Monzo (in analyzing Aristoxenus: 318 = 53*6) |
| 384 |
pentamu (5mu), a MIDI pitch-bend unit: 25 (= 32) 5mus per semitone, 25 * 12 = 384 5mus per octave. |
| 441 |
2004 -- Gene Ward Smith - a very strong 5 or 7 limit system, along with 612 a good way to tune ennealimmal. |
| 494 |
2004 -- Gene Ward Smith - strong 11-15 limit system, and still good as a 17-limit system. |
| 512 |
29 units per octave. 1980s -- tuning resolution of some electronic instruments, notably Ensoniq VFX and VFX-SD. |
| 540 |
dexl, named by Joseph Monzo after its Roman numeral (DXL). 2023 -- Joseph Monzo, as a replacement for cents to measure 43-limit JI |
| 581 |
2013 -- Scott Dakota 2015 -- Cam Taylor 2016 -- Joseph Monzo -- for use as a unit of interval measurement without need for decimal places, strongest 3-digit EDO for 23-limit JI. |
| 600 |
50 units per Semitone = 12 * 50 units per octave. 1898 -- Widogast Iring -- "iring" unit of interval measurement 1932 -- Joseph Yasser "centitone" unit of interval measurement |
| 612 |
51 (= 3 * 17) units per semitone = 22 * 32 * 17 units per octave; an excellent unit of interval measurement for 11-limit JI. before 1875 -- Captain J. W. F. Herschel (cited by Bosanquet) 1917 -- Josef Sumec c.1970 -- Gene Ward Smith -- for interval measurment, an analogue of cents 2002 -- Joseph Monzo (in analyzing Werckmeister III) |
| 665 |
(a remarkably close approximation to pythagorean tuning) before 1975 -- Jacques Dudon 1980s? -- Marc Jones -- see satanic comma |
| 730 |
1835 -- Wesley Woolhouse -- his unit of measurement for 5-limit JI, and an analogue of cents; 60 5/6 degrees per Semitone. |
| 768 |
hexamu (6mu), a MIDI pitch-bend unit: 26 (= 64) 6mus per semitone, 26 * 12 = 768 6mus per octave. 1980s-2000s -- Tuning resolution of many electronic instruments, including several by Yamaha, Emu, and Ensoniq; also the resolution of some early sequencer software, including Texture. 1980s-2000s -- Joseph Monzo (using Texture software in 1980s, then using computer soundcards with 6mu resolution in 1990s and 2000s.) 1980s-2000s -- myriad artists using MIDI hardware. 2003 -- Joseph Monzo -- proposed as de facto hardware tuning standard |
| 1000 |
millioctave, an interval measurement, an analogue of cents: 1000 = 23 * 53 = 83 1/3 units per Semitone. 1980s -- Csound software: its "oct" pitch format 1993 -- Mark Lindley (in his book Mathematical Models of Musical Scales) |
| 1024 |
210 (= 1024) units per octave = 85 1/3 units per Semitone; an analogue of cents. 1980s -- Tuning resolution for many synthesizers with tuning tables, including the popular Yamaha DX, SY and TG series 1990-95 -- Joseph Monzo (tuning resolution of Yamaha TG-77) |
| 1200 |
1875 -- Alexander Ellis (his unit of measurement, called cents, 100 per 12-tET semitone) 1980s-2000s -- many synthesizers and soundcards with 1-cent resolution give a 768-out-of-1200-edo subset tuning. |
| 1536 |
heptamu (7mu), a MIDI pitch-bend unit; 27 = 128 7mus per Semitone; 12 * 27 = 1536 7mus per octave |
| 1700 |
2002 -- Margo Schulter (for interval measurement, called "iota") |
| 1728 |
19?? -- Paul Beaver (rendered as 123) |
| 2460 |
mina (short for "schismina"); 233-EDA (233 equal divisions of the apotome); quite close to 1/2 cent. 2004 -- The largest ET that can be notated in the Sagittal notation system. 2004 -- Gene Ward Smith, George Secor, Dave Keenan |
| 3072 |
oktamu (8mu), a MIDI pitch-bend unit: 28 (= 256) 8mus per Semitone; 12 * 28 = 3072 8mus per octave. 1990s -- Apple's QuickTime Musical Instruments tuning spec |
| 3125 |
2004 -- Gene Ward Smith - a strong 7 or 9 limit system, but mentioned here because it is 5^5, which might be useful for something. 2007 - Joseph Monzo - advocated as a unit of interval measurement for 7-limit JI. |
| 4296 |
358 units per semitone 1992 -- Marc Jones (used as most convenient UHT [ultra-high temperament] to measure 5-limit just intonation intervals) |
| 6144 |
enneamu (9mu), a MIDI pitch-bend unit: 29 (= 512) 9mus per Semitone; 12 * 29 = 6144 9mus per octave. |
| 8539 |
tina; 809-EDA (809 equal divisions of the apotome) 2007 -- Joseph Monzo -- for use as a unit of interval measurement without need for decimal places, strong thru 31-limit JI and also good for 41. |
| 10600 |
1965 -- M. Ekrem Karadeniz -- his unit of measurement, called türk-sents, 200 units per 53-edo comma. |
| 12288 |
dekamu (10mu), a MIDI pitch-bend unit: 210 (= 1024) 10mus per Semitone; 12 * 210 = 12288 10mus per octave. |
| 24576 |
endekamu (11mu), a MIDI pitch-bend unit: 211 (= 2048) 11mus per Semitone; 12 * 211 = 24576 11mus per octave. |
| 30103 |
jot 1864 -- Augustus De Morgan -- his unit of measurement; chosen because of its closeness to log10(2) * 100,000. |
| 31920 |
2007 -- Gene Ward Smith, Joseph Monzo -- for use as a unit of interval measurement which is both strong (i.e., low logflat badness) and consistent thru 41-limit JI. |
| 36829 |
(198? -- approximation to John Brombaugh's scale of temperament units.) |
| 46032 |
flu -- useful for discussing 5-limit tempering. 2004 -- Gene Ward Smith - The "Diophantine clarity" division: pythagorean-comma = 900 flus, syntonic-comma ("Didymus comma") = 825 flus, therefore schisma = 75 flus. The flu system tempers the atom out of the discussion. Gene recommeds it as a replacement for Tuning Units. |
| 49152 |
dodekamu (12mu), a MIDI pitch-bend unit: 212 (= 4096) 12mus per Semitone; 12 * 212 = 49152 12mus per octave; formerly called cawapu. 1980s -- pitch-bend resolution of CakewalkTM and many other popular sequencer programs. |
| 58973 |
5587-EDA (5587 equal divisions of the apotome) 2007 -- Joseph Monzo -- for use as a unit of interval measurement without need for decimal places, strong and consistent thru 41-limit JI. |
| 98304 |
tridekamu (13mu), a MIDI pitch-bend unit: 213 (= 8192) 13mus per Semitone; 12 * 213 = 98304 13mus per octave. 1983 -- the maximum resolution possible in MIDI pitch-bend |
| 196608 |
tetradekamu (14mu), a MIDI pitch-bend unit: 214 (= 16384) 14mus per Semitone; 12 * 214 = 196608 14mus per octave; formerly called midipu. 1983 -- finest possible resolution in the MIDI tuning Spec. 1999 -- MTS (MIDI tuning standard) |
|
Notes:
|
Any tuning system which divides the octave (2/1) into n aliquot parts is termed an n-tone Equal Temperament. Mathematically, an Equal Temperament is a geometric series and each degree is a logarithm to the base 2n.
[Note from Monzo: the base is 2 only in octave-equivalent equal-temperaments. It is possible to construct an equal temperament using any number as a base, as noted below. An example would be to divide the perfect 12th, which has the ratio 3:1, into equal steps (as in the Bohlen-Pierce scale); this is a geometric series where each degree is a logarithm to the base 3n.]
Because of the physiology of the human auditory system, the successive intervals of Equal Temperaments sound perceptually equal over most of the audible range.
It is also possible to divide intervals other than the octave as in the recent work of Wendy Carlos (Carlos,1986), but musical examples are still rather uncommon.
The tonalsoft.com website is almost entirely the work of one person: me, Joseph Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
