diatonic genus
In ancient Greek theory, one of the three basic types of genus. It had a characteristic interval of approximately a "tone" at the top of the tetrachord, then two successive intervals of approximately a "tone" and then a semitone at the bottom, making up a 4/3 "perfect 4th".
Below is a graph showing the comparative structures of tetrachords for the diatonic genus as explained by various ancient theorists. A detailed examination of each proposal follows.
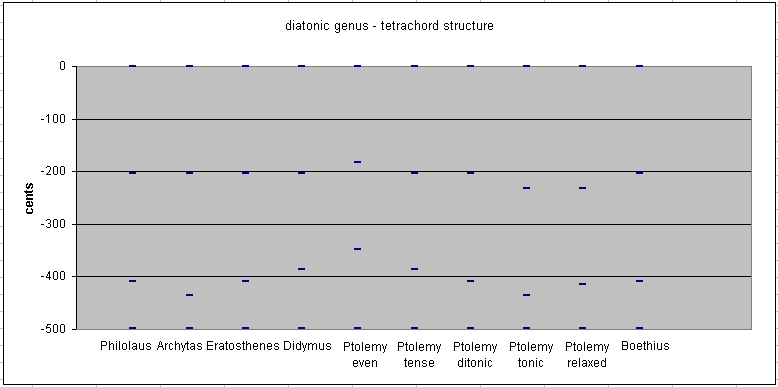
Philolaus (and Eratosthenes, Ptolemy "ditonic diatonic", and Boethius)
string-length proportions: 192 : 216 : 243 : 256
note ratio ~ cents
mese 1/1 0
> 8:9 ~ 203.9100017 cents
lichanos 8/9 - 203.9100017
> 8:9 ~ 203.9100017 cents
parhypate 64/81 - 407.8200035
> 243:256 ~ 90.22499567 cents
hypate 3/4 - 498.0449991
The earliest measurement of the diatonic genus is by Philolaus. Descending from the top note, it divides the 4:3 "perfect-4th" bounding the tetrachord into two successive Pythagorean 9:8 tones and a Pythagorean 256:243 "limma" semitone.
Extended to a full "octave", this version of the diatonic genus could be tuned using the method of "tuning by concords", that is, successive 3:2 "perfect-5ths" and 4:3 "perfect-4ths" up and down from the starting note mese.
Archytas (and Ptolemy "tonic diatonic")
string-length proportions: 1512 : 1701 : 1944 : 2016 (reduced 168:189:216:224)
note ratio ~ cents
mese 1/1 0
> 8:9 ~ 203.9100017 cents
lichanos 8/9 - 203.9100017
> 7:8 ~ 231.1740935 cents
parhypate 7/9 - 435.0840953
> 27:28 ~ 62.96090387 cents
hypate 3/4 - 498.0449991
Archytas used the same tuning for the note above the bottom (parhypate) in all three of his genera, making it a 28:27 above the bottom note (hypate) and a 9:7 below the top note (mese); all other ancient Greek theorists allowed parhypate to be moveable along with lichanos, its placement depending on the genus. Winnington-Ingram speculated that perhaps the reason for this strange interval was that it was important for the note above the 28:27 to be in a 7:6 "septimal minor-3rd" ratio to the note which lies a 9:8 "tone" below its lower note.
Thus, whereas the highest interval in his diatonic tetrachord is the same Pythagorean 9:8 tone indicated by Philolaus, the middle interval is the larger 8:7 "septimal tone".
The next description to come down to us, by Eratosthenes, specifies the same ratios as Philolaus.
Didymus
string-length proportions: 24 : 27 : 30 : 32
note ratio ~ cents
mese 1/1 0
> 8:9 ~ 203.9100017
lichanos 8/9 - 203.9100017
> 9:10 ~ 182.4037121
parhypate 4/5 - 386.3137139
> 15:16 ~ 111.7312853
hypate 3/4 - 498.0449991
Didymus kept the Pythagorean 9:8 tone as his highest interval, but replaced the middle interval with the 5-limit 10:9 "lesser tone", thus making the interval between parhypate and the top note (mese) the 5-limit 5:4 "major-3rd". The small interval at the bottom is thus the 5-limit 16:15 "diatonic semitone".
Ptolemy "even diatonic" (homalon, also translated "equable" or "smooth")
string-length proportions: 9 : 10 : 11 : 12
note ratio ~ cents
mese 1/1 0
> 9:10 ~ 182.4037121 cents
lichanos 9/10 - 182.4037121
> 10:11 ~ 165.0042285 cents
parhypate 9/11 - 347.4079406
> 11:12 ~ 150.6370585 cents
hypate 3/4 - 498.0449991
The string-length proportions of Ptolemy's "even diatonic" have the smallest-number consecutive ratios which can describe a four-fold division of the 4:3 "perfect-4th". The top interval is thus the 5-limit 10:9 "lesser tone", the middle interval is the 11:10 "undecimal tone", and the bottom interval is the 12:11 "neutral 2nd" functioning as a very wide semitone.
Ptolemy "tense diatonic" (syntonon, frequently translated poorly as "intense")
string-length proportions: 36 : 40 : 45 : 48
note ratio ~ cents
mese 1/1 0
> 9:10 ~ 182.4037121 cents
lichanos 9/10 - 182.4037121
> 8:9 ~ 203.9100017 cents
parhypate 4/5 - 386.3137139
> 15:16 ~ 111.7312853 cents
hypate 3/4 - 498.0449991
Ptolemy's "tense diatonic" is similar to Didymus in that it makes use of both size of "whole tone", the Pythagorean 9:8 and the 5-limit 10:9 -- however, Ptolemy uses them in reverse order, putting the smaller 10:9 at the top and the larger 9:8 in the middle. This leaves the 16:15 "diatonic semitone" at the bottom, as with Didymus.
Ptolemy's "ditonic diatonic" is the same as Philolaus's classic Pythagorean description, and his "tonic diatonic" is the same as Archytas's.
Ptolemy "relaxed diatonic" (malakon, frequently translated poorly as "soft")
note ratio ~ cents
mese 1/1 0
> 7:8 ~ 231.1740935 cents
lichanos 7/8 - 231.1740935
> 9:10 ~ 182.4037121 cents
parhypate 63/80 - 413.5778057
> 20:21 ~ 84.46719347 cents
hypate 3/4 - 498.0449991
Ptolemy's "relaxed diatonic" has the 8:7 "septimal tone" as its top interval, the 5-limit 10:9 "lesser tone" in the middle, and the small 21:20 semitone at the bottom.
Boethius gave the same classic Pythagorean description of the diatonic as that used by Philolaus.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
