Ganassi's well-temperament

© 1995-2001 by Joe Monzo

--- In spiritual_tuning@y..., message 170 (Sun Jun 3, 2001 8:13 pm), John Chalmers wrote:

> Alas, [prime factors] 17 and 19 combine with powers of 2 and 3 to generate
> intervals nearly indistinguishable from 12-tet. A pretty good
> approximation to 12-tet may be made from a repeated series
> of pitches related as 16:17:18:19 ( I have references
> somewhere to Integer Ratio Chromatic Scales constructed just
> this way).

Sylvestro Ganassi's treatise (1543, Regula Rubertina, chapter 4) is the one I know which presents the chromatic scale this way.

While at first glance it does seem to give "a pretty good approximation to 12-tet", a deeper look into this tuning reveals that it is an interesting rational form of a well-temperament.

Here is a table illustrating the scale, with cents given above the nominals, and string-length proportions below:

   0   89  182  281 386 498  597  702  791  884  983 1088   0

  C  C#/Db  D  D#/Eb  E   F  F#/Gb  G  G#/Ab  A  A#/Bb  B   C

 120  114  108  102  96  90   85   80   76   72   68   64  60

  30        27       24            20   19   18   17   16  15
  24                     18   17   16                      12
  20   19   18   17  16  15                  12            10

So you can see that it is two fully chromatic tetrachords with the proportions 20:19:18:17:16:15, connected by a "tone of disjunction" which is divided 18:17:16.

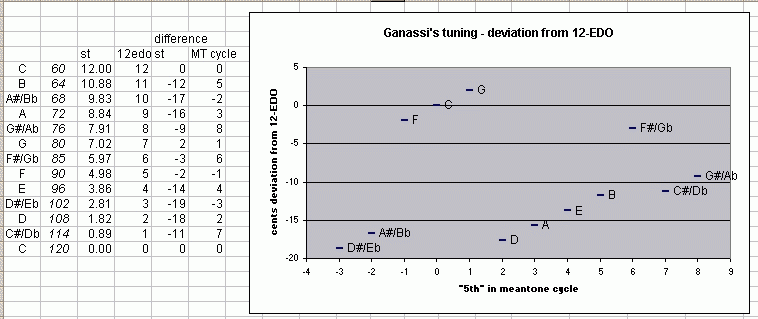
Here is a diagram of the pitches arranged in a typical meantone cycle of "5ths", showing the deviation of these 12 pitches from today's standard 12-EDO:

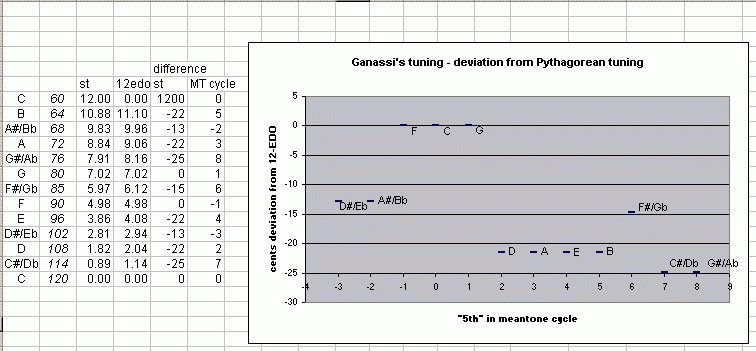
And here is a diagram of the same cycle, showing the deviation of these 12 pitches from Pythagorean tuning, in which each "5th" in the cycle would be a perfect 3:2 ratio:

The cents values show that it is a well-temperament, with uneven distribution of "error" from either 12-EDO or Pythagorean.

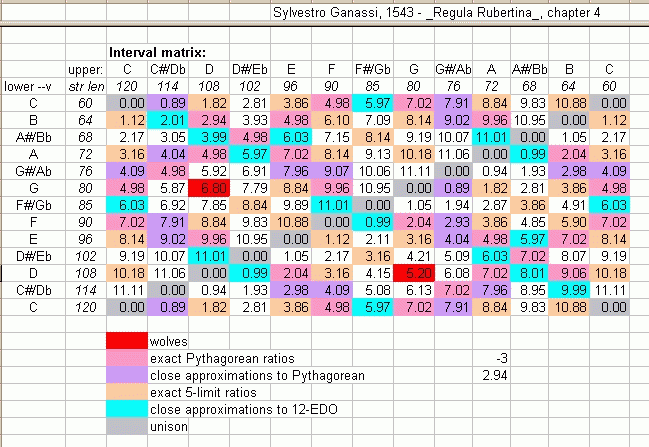
Here is the interval matrix of this tuning:

The interval matrix shows that this tuning gives several exact Pythagorean "4ths" and "5ths" and 5-limit JI "major 2nd/3rd/6th/7ths". The "minor" variety of these intervals are narrower than either Pythagorean or 5-limit, in a few cases suggesting the 7-limit flavor of "minor 3rd/7th".

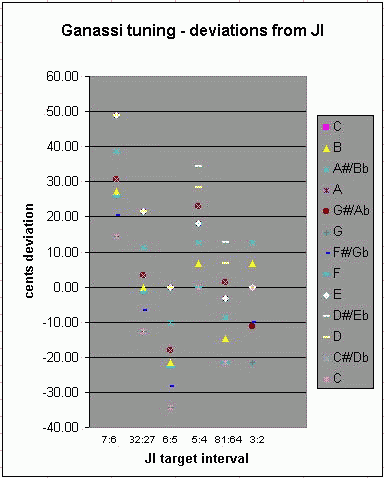
From the interval matrix I have constructed a table showing deviation from the "perfect 5th" and from Pythagorean and 5-limit JI "3rds" (and from 7:6), useful in analyzing the properties of this tuning in relation to "common-practice" (Eurocentric, c. 1600-1900) triadic harmony.

Here is the graph:

Deviations from JI intervals (in cents):

           7:6  32:27  6:5  5:4  81:64   3:2
  "root"
    B     +27     0   -22  + 7   -15    + 7
  A#/Bb   +39   +11   -10  +13   - 9    +13
    A     +49   +22     0  +18   - 3      0
  G#/Ab   +31   + 3   -18  +23   + 1    -11
    G     +14   -13   -34    0   -22    -22
  F#/Gb   +20   - 7   -28    0   -22    -10
    F     +26   - 1   -23    0   -22      0
    E     +49   +22     0  +18   - 3      0
  D#/Eb   +49   +22     0  +34   +13      0
    D     +49   +22     0  +28   + 7      0
  C#/Db   +31   + 3   -18  +23   + 1      0
    C     +14   -13   -34    0   -22      0

(click on the links in the text below to hear mp3s of the chords)

This table shows that the only "good" triads, which provide exact proportions of 4:5:6 for "major" and 1/(4:5:6) for "minor", are "C" major and "F" major, and "D" minor, "D#" minor, "E" minor, and "A" minor.

Some comments on the rest of the "major" triads:

"G" major gives a 5:4 "major 3rd" but the 22-cent-flat "wolf 5th". "F#/Gb" major gives a 5:4 "major 3rd" with a "5th" much closer to 3:2.

"A" major, "E" major, and "C#/Db" major all give exact 3:2s for the "5th" and an extremely close approximation to the 81:64 Pythagorean "major 3rd", and "D" major is similar but sounds quite out-of-tune with a slightly higher "3rd".

"B" major gives a "major 3rd" and a "5th" that are both ~7 cents wider than 4:5:6, and "A#/Bb" major gives deviations of ~13 cents wider for both.

"D#/Eb" major is similar to "D" major in that it gives an exact 3:2 "5th" but an even higher "major 3rd", and "G#/Ab" major gives a very good approximation to the Pythagorean "major 3rd" but the "5th" is ~11 cents narrower than 3:2.

And for the rest of the "minor" triads:

Of the remaining 3 "minor" triads which have a perfect 3:2 "5th", "F" minor and "C#/Db" minor give a good approximation to the Pythagorean 32:27 "minor 3rd", and "C" minor gives a dark narrow "3rd" which is about halfway between the 7:6 and the Pythagorean "minor 3rd".

"G" minor has this same low "minor 3rd", but its "5th" is the very flat "wolf 5th".

"F#/Gb" minor and "G#/Ab" minor both have decent approximations to the Pythagorean "minor 3rd" and a "5th" narrower by ~10 and ~11 cents respectively from 3:2, and "B" minor gives an exact Pythagorean "minor 3rd" with a "5th" that is ~7 cents wider than 3:2.

Lastly, "A#/Bb" minor gives almost the same error for its wide Pythagorean "minor 3rd" and "5th"; its "minor 3rd" is actually about midway between the Pythagorean and 6:5.

Updated:

2001.05.31
2001.10.14 (Thanks to Rick McGowan for pointing out a typo.)